Boyd T.J.M., Sanderson J.J. The Physics of Plasmas

Подождите немного. Документ загружается.

6.3 Waves in cold plasmas 217

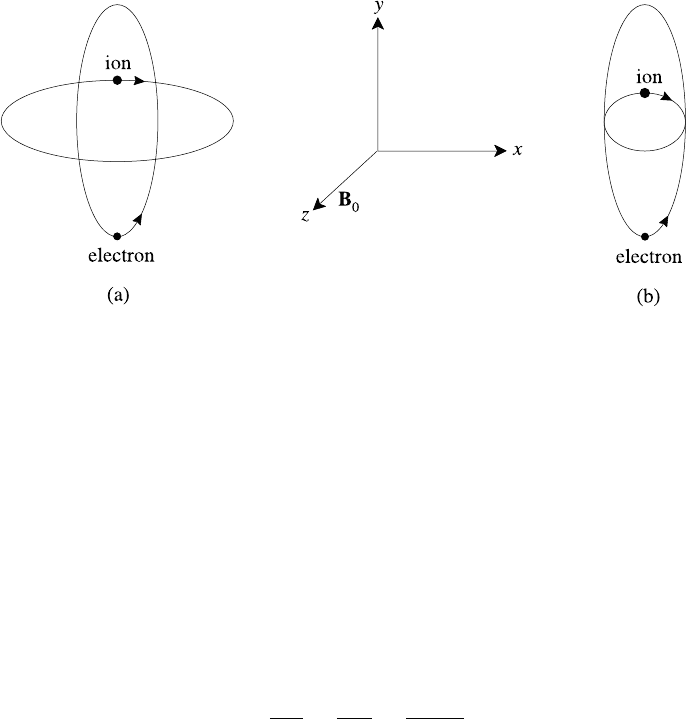
Fig. 6.8. Average particle orbits in lower hybrid wave for (a) ω<ω

, (b) ω → ω

= (ω

+ 

)

1/2

≈ (ω

+ 

)

1/2

, and the resonance is between the

electron motion and the electric ﬁeld as can be seen from (6.62). Poisson’s equation

provides an order of magnitude for the electric ﬁeld, E ∼ n

e(x)

/ε

, so that,

using (6.64) for (y)

, (6.62) gives

(x)

∼ (ω

+ 

)(x)

This is a second example of the symmetries found in the cold plasma wave theory

between electron properties at high frequency and ion properties at low frequency,

the ﬁrst being the simple cyclotron resonances.

A ﬁnal observation from (6.58) is that

P =

−D

L − R

L + R

so that in general the X mode is elliptically polarized although this becomes linear

at the resonances (S → 0), as already noted, and circular at the cut-offs; the wave

is RCP at ω = ω

(R = 0) and LCP at ω = ω

(L = 0).

6.3.4 Wave normal surfaces

Much information about cold plasma waves has been obtained by examining the

special cases of parallel and perpendicular propagation. We shall now show that by

combining the results of the last two sub-sections with some of the properties of the

general dispersion relation we can make deductions about the waves propagating

at oblique angles (0 <θ <π/2) to the magnetic ﬁeld B

First, let us summarize some of the properties of the solutions of the general

dispersion relation (6.31):

218 Waves in unbounded homogeneous plasmas

(i) There are two solutions which are distinct except where the discrimi-

nant (6.34) vanishes. Except for the discrete points in parameter space where

the surfaces RL = PS and PD = 0 intersect, the discriminant can vanish

only at θ = 0orπ/2. For oblique propagation, therefore, we can use this

distinction to label one of the solutions the fast (F) wave and the other the

slow (S) wave. By extrapolation this labelling can be used at θ = 0andπ/2,

also, even when the discriminant vanishes at these angles. Since n

= c

we have n

< n

(ii) The phase velocity of a propagating wave may remain ﬁnite at all angles or

may tend to zero (k →∞) as θ → θ

res

. In the latter case the wave propagates

in only one of the cones shown in Fig. 6.4. If both waves propagate and one

of them suffers a resonance this must be the S wave. It can be shown (see

Stix (1992)) that, if both waves propagate, at most one of them can suffer a

resonance.

(iii) If the waves propagate at θ = 0 one of them is the R wave and the other the L

wave. These, also, are useful identifying labels but it should be remembered

that the dispersion relations n

= R, L apply only at θ = 0 and the properties

of RCP and LCP, likewise, do not apply at oblique propagation.

(iv) Similarly, the O and X labels may be used if the waves propagate at θ =

π/2 but, here again, one cannot extrapolate the dispersion relations n

= P,

= RL/S nor is it true that the dispersion relation of the O wave remains

independent of the magnetic ﬁeld for θ<π/2.

All this information may be neatly summarized by drawing the wave normal

surfaces at any given point in parameter space. The wave normal surface is a plot

of the phase velocity in spherical polar coordinates but since there is no dependence

on the azimuthal coordinate, φ, this reduces to a plane polar plot of v

versus θ , the

surface being generated by rotation of the ﬁgure about the polar (

z) axis. In view of

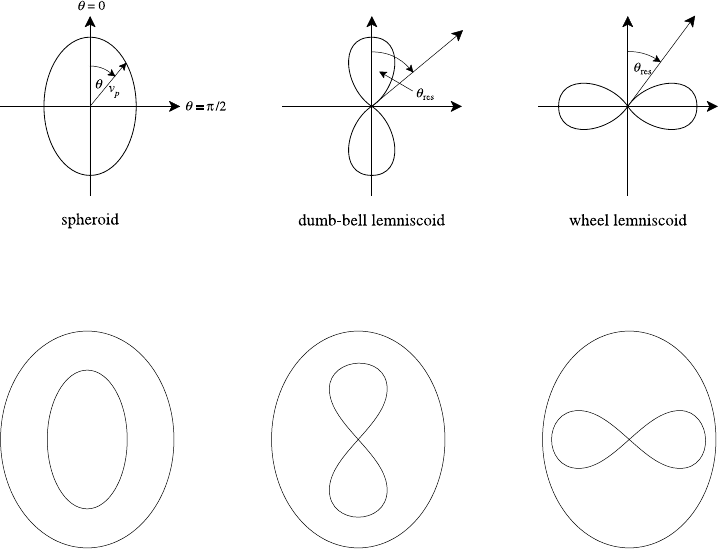
properties (i) and (ii) the only possible surfaces are the spheroid and lemniscoids

shown in Fig. 6.9; the lemniscoid with propagation at θ = 0 is called a dumb-bell

and that with propagation at θ = π/2 is called a wheel (imagine the polar plots

rotated about the polar axis).

If both waves propagate, the permissible combinations of wave normal surfaces

are two spheroids or a spheroid and a lemniscoid as illustrated in Fig. 6.10. Except

for the discrete points of parameter space mentioned in (i) the wave normal surfaces

may be tangential only at θ = 0orπ/2. Clearly the outer surface is the F wave and

we may add, as appropriate, the labels R or L at θ = 0 and O or X at θ = π/2. For

example, the wave normal surfaces for the compressional and shear Alfv

en waves

in the low frequency regime (ω < 

,ω

) correspond to a spheroid and dumb-bell

6.3 Waves in cold plasmas 219

Fig. 6.9. Wave normal surfaces.

Fig. 6.10. Possible wave normal surfaces when both modes propagate.

lemniscoid, respectively. Ideal MHD suggests that these surfaces are tangential at

θ = 0 but (6.54) shows that this is true only in the limit ω → 0.

Now we come to the most important statement about the wave normal surfaces

for the compilation of a general classiﬁcation scheme. The topology of the surfaces

can change only at the cut-offs and principal resonances. For example, at a cut-off

→∞so the F wave solution changes sign at inﬁnity, i.e. a spheroid disappears.

At a principal resonance v

→ 0 so a spheroid may become a lemniscoid. The

converse of this occurs when θ

res

→ 0(π/2) for a wheel (dumb-bell) lemniscoid.

Finally, lemniscoids disappear when θ

res

→ 0(π/2) for the dumb-bell (wheel).

This means that the cut-offs and principal resonances are the natural classiﬁcation

boundaries in parameter space.

For a two-component plasma, parameter space is two dimensional and can be

represented by a diagram with α

= ω

/ω

as abscissa and β

=|



|/ω

ordinate; thus, the horizontal axis is the direction of increasing density or decreas-

ing frequency and the vertical axis is the direction of increasing magnetic ﬁeld

or decreasing frequency. The cut-offs and principal resonances divide this space

220 Waves in unbounded homogeneous plasmas

Fig. 6.11. Subdivision of parameter space by principal resonance and cut-off curves.

into thirteen regions which are numbered† alternately left and right of the plasma

cut-off P = 0 (i.e. α

= 1) and with increasing β

, as shown in Fig. 6.11; the

ﬁgure is illustrative and is not drawn to any realistic scale of mass ratio.

Since all the boundaries of parameter space represent a speciﬁc frequency we

can deduce all the wave normal surfaces for the thirteen regions from the dispersion

diagrams for the R, L, O and X waves (see Figs. 6.2 and 6.5–6.7). These tell us

which of these waves propagate at θ = 0 and π/2 and, if both propagate, by

comparing the asymptotic behaviour, which is the F and which the S wave. For

example, Fig. 6.2 shows that the O mode propagates only for ω>ω

, i.e. in the

odd numbered regions to the left of P = 0. Also, by comparing Figs. 6.2 and

6.7 we see that the X mode is the F wave for ω>ω

(as k → 0, ω

→ ω

and ω

→ ω

with ω

>ω

). Similarly, from Figs. 6.5 and 6.6, both R and

L modes propagate for ω>ω

and the R mode is clearly the F wave. Thus,

in region 1 (ω>ω

) both wave normal surfaces are spheroids, the F wave

having the labels RX and the S wave LO. In crossing the R = 0 (ω = ω

)

boundary the RX mode is cut-off (v

→∞) and only the LO mode propagates in

† This numbering system is not universal; our choice follows Allis et al. (1963).

6.3 Waves in cold plasmas 221

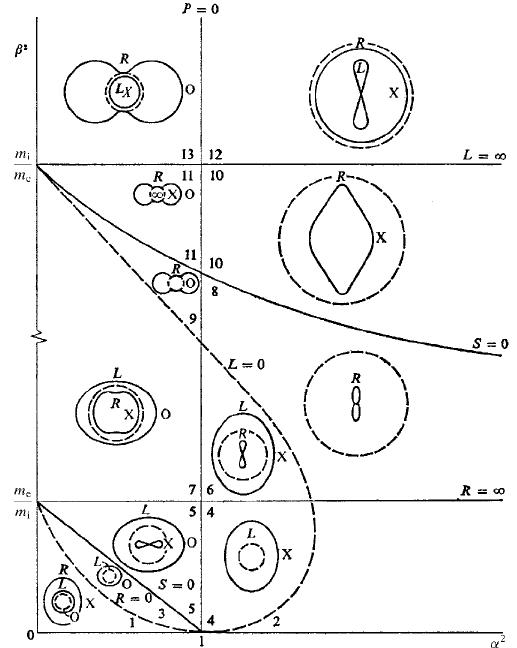
Fig. 6.12. CMA diagram showing the wave normal surfaces for a cold plasma. The sur-

faces are not drawn to scale but the dashed circle represents the velocity of light in each

region (after Allis et al. (1963)).

region 3. In this manner one can traverse the whole of parameter space identifying

the wave normal surfaces† (see Exercise 6.8) and obtain Fig. 6.12, which is called

the Clemmow–Mullaly–Allis (CMA) diagram. The sketches of the wave normal

surfaces in Fig. 6.12 are schematic, merely indicating type. The actual shape varies

across the region; for example, the spheroidal wave normal surface of the SLX

mode in region 13 pinches in (v

→ 0) at θ = 0 as one approaches the ω = 

boundary in anticipation of the disappearance of the L mode on crossing this

boundary into region 11. Note that the S wave does not disappear completely at

this boundary but its wave normal surface changes from a spheroid to a wheel

lemniscoid; such a change is called a re-shaping transition. On the other hand, in

† There is one slight complication with the O and X labels in region 7; they switch waves across the surface

RL = PS because n

− n

= (RL − PS)/S.

222 Waves in unbounded homogeneous plasmas

crossing the same boundary from region 12 to region 10, the cut-off of the L mode

does mean the complete disappearance of the S wave; this is called a destructive

transition. In contrast, the F wave experiences no signiﬁcant change on crossing

this boundary and is said to undergo an intact transition.

6.3.5 Dispersion relations for oblique propagation

Since the boundaries of parameter space are all speciﬁed by particular frequencies

we can use this to ﬁnd approximate dispersion relations by comparing ω inagiven

region with its bounding frequencies and either expanding the coefﬁcients in (6.32)

in the small parameter ω/ω

or ω

/ω (where ω

is the frequency at a boundary of

the region) or approximating the coefﬁcients by letting ω → ω

. We have used this

technique already in the low frequency regime (region 12) by assuming ω/



1 and ω/ω

 1 and then later letting ω → 

. It is particularly useful when

comparing ω with the plasma and cyclotron frequencies for, as one can see from

(6.29), the parameters R, L , S and P can all be expressed in terms of α

= ω

/ω

=|



|/ω

, β

= 

/ω and β

=|

|/ω:

S = 1 −

(1 − β

)

(1 − β

)(1 − β

)

R = 1 −

(1 + β

)(1 − β

)

L = 1 −

(1 − β

)(1 + β

)

P = 1 − α











(6.65)

Low frequency regime (ω<

)

Let us use this method to recover the dispersion relations in region 12 for arbitrary

angles of propagation. We may choose ω  

and ω  ω

giving

S, R, L ≈ 1 +α

/β

= 1 + γ(γ= c

)

and

P ≈−α

Substituting these approximations in (6.32) we get

A ≈ 1 + γ − (1 + γ + α

) cos

B ≈ (1 +γ)[(1 + γ − α

) − (1 + γ + α

) cos

θ]

C ≈−α

(1 + γ)

6.3 Waves in cold plasmas 223

and (6.31) factorizes to give the solutions

= 1 +γ (6.66)

(1 + γ)

(1 + γ + α

) cos

θ − (1 + γ)

(6.67)

The ﬁrst solution is independent of θ so the wave normal surface is a sphere. The

second solution gives real values of n only for 0 ≤ θ ≤ θ

res

, where cos

res

(1 + γ)/(1 + γ + α

) so this wave normal surface is a dumb-bell lemniscoid

conﬁrming the statement made in Section 6.3.4. The ideal MHD solutions, (4.122)

and (4.123) with c

= 0, are recovered in the non-relativistic and low frequency

limits γ,α

→∞.

Near the ion cyclotron resonance (ω → 

)

Next let us ﬁnd the dispersion relations for oblique propagation as we approach the

ion cyclotron resonance at ω = 

. Here we let ω = 

(1 − ), where 0 < 1,

giving S ≈ γ/(2), R ≈ 1 +γ/2, L ≈ γ/ and P ≈−γ/µ, with µ ≡ 

/|

 1. Substituting these approximations in (6.32) we get

A ≈

2µ

(µ sin

θ − 2 cos

θ)

B ≈−

2µ

(1 + cos

θ)

C ≈−

2µ

(2 + γ)

Since both µ and  are small quantities it is clear that B

|4AC| so that,

expanding the discriminant, the approximate solutions of (6.31) are

2 + γ

1 + cos

(6.68)

and

γ(1 +cos

θ)

(−µ sin

θ + 2 cos

θ)

(6.69)

The ﬁrst of these solutions, which may be written

(1 + cos

θ)

1 + 2v

≈ k

(1 + cos

θ) (6.70)

is the generalization of (6.53) for compressional Alfv

en waves propagating at ar-

bitrary angles as ω → 

. It shows the increase in phase velocity (v

≈ v

√

2) at

224 Waves in unbounded homogeneous plasmas

θ = 0asω → 

(see Fig. 6.5); the wave normal surface is still a spheroid but no

longer a sphere.

The more interesting solution is (6.69) which is the dispersion relation for ion

cyclotron waves. It has a resonance at tan

res

= 2/µ, conﬁrming that θ

res

→ 0

as  → 0 (i.e. ω → 

). Dropping the term in µ and rewriting (6.69) as n

≈

S(1 + cos

θ)/cos

θ, where S ≈−ω



/|

|(ω

− 

),weget,

≈

cos

1 + cos





− ω





(6.71)

as the generalization of (6.57) for ion cyclotron waves.

High frequency regime

Simple dispersion relations are obtainable whenever the discriminant (B

−4AC)

is a perfect square or can be expanded. Although the ﬁrst of these possibilities

(which yielded the solutions (6.66) and (6.67)) occurs rarely, it is clear from (6.34)

that one can always ﬁnd an expansion by letting θ → 0orπ/2; these denote the

quasi-parallel (Q



) and quasi-perpendicular (Q

⊥

) approximations, respectively.

This method of approximation is particularly appropriate in the high frequency

regime which we consider next.

If ω |



1/2

it follows from (6.65) that

S ≈ 1 − α

/(1 − β

)

R ≈ 1 −α

/(1 − β

)

L ≈ 1 − α

/(1 + β

)

P = 1 − α











(6.72)

and, since α

≈ ω

/ω

, it is clear that the effect of the ions on wave propagation

is negligible. This regime, which embraces all of regions 1–8 in the CMA diagram

(provided we are not too close to the S = 0 (ω = ω

) boundary in region 8), has

been studied extensively in the context of waves in the ionosphere and gives rise to

magneto-ionic theory.

To establish contact with this theory it is convenient to cast the solution of (6.31)

in the form (see Exercise 6.11)

= 1 −

2(A − B + C)

2A − B ∓ (B

− 4AC)

1/2

(6.73)

Using the approximations (6.72) this becomes

= 1 −

2α

(1 − α

)

2(1 − α

) − β

sin

θ ∓ 

(6.74)

6.3 Waves in cold plasmas 225

where

 = [β

sin

θ + 4β

(1 − α

)

cos

θ]

1/2

(6.75)

Equation (6.74) is the collisionless Appleton–Hartree dispersion relation. We shall

consider it in the limits:



: β

sin

θ  4(1 − α

)

cos

θ (6.76)

⊥

: β

sin

θ  4(1 − α

)

cos

θ (6.77)

Quasi-parallel (θ → 0)

The Q



solutions are given by

≈ 1 −

1 ∓ β

cos θ

(6.78)

and comparison with (6.72) shows that the plus and minus signs correspond, in the

limit θ → 0, to the L and R waves, respectively. Thus, (6.78) is the generalization,

in the Q



limit, of (6.51) and (6.52), giving

= k

ωω

ω ∓|

|cos θ

and showing that the high frequency dispersion relations for oblique propagation

are obtained from (6.51) and (6.52) by replacing |

| by |

|cos θ , i.e. the com-

ponent of the ﬁeld along the direction of wave propagation.

For β

≥ 1 the R wave has a resonance at cos θ = β

−1

. According to (6.78) this

occurs for any value of α

but near a resonance we need to make a more careful

examination of the approximation. This is best done directly from (6.37) which

gives

tan

res

(α

− 1)(β

− 1)

(α

+ β

− 1)

− 1

1 + β

/(α

− 1)

(6.79)

showing that there is no real solution and, therefore, no resonance for α

< 1 and

conﬁrming that the resonance occurs at cos θ = β

−1

provided β

 α

−1, which

is consistent with the Q



approximation (6.76).

Quasi-perpendicular (θ → π/2)

Turning to the Q

⊥

approximation we ﬁnd from (6.74) the solutions

1 − α

cos

(6.80)

226 Waves in unbounded homogeneous plasmas

and

(1 − α

)

− β

sin

(1 − α

) − β

sin

(6.81)

For α

< 1 the ﬁrst of these has n

> 0 for all θ and reduces to (6.47) as θ → π/2

so this is the O mode. Rearranging (6.80) we get

− ω

(ω

+ k

) + k

cos

θ = 0

with the approximate solutions

≈ (ω

+ k

)



1 −

cos

(ω

+ k

)



(6.82)

and

≈

cos

1 + ω

(6.83)

Only the ﬁrst solution (6.82) has α

< 1 so this is the generalization of (6.47)

showing a marginal decrease in phase velocity for propagation of the O mode

away from the perpendicular direction. The second solution (6.83) has α

> 1 and,

from (6.80), we see that it propagates only for 0 ≤ θ<cos

−1

(α

−1

). This is, in fact,

the Q

⊥

approximation of the R mode dispersion relation for α

,β

> 1, as we can

see from (6.79). The symmetry of this equation with respect to α and β shows that

for 1 <α

 β

−1 the resonance occurs at cos θ = α

−1

. Given that region 6 has

1 <α

< 2 and 1 <β

< |

|/

− 1, (6.83) is appropriate in this region except

near the electron cyclotron resonance or θ = 0.

The second solution (6.81) in the Q

⊥

approximation is the dispersion relation

for the X mode. For perpendicular propagation this was given by (6.59) and if we

substitute for R, L and S from (6.72) in this equation we get

(1 − α

)

− β

1 − α

− β

Comparing this with (6.81) we see that the high frequency dispersion relation for

the X mode, in the Q

⊥

approximation, is obtained simply by replacing |

| by

|

|sin θ , i.e. the component of the ﬁeld perpendicular to the direction of wave

propagation. The resonance occurs at

sin

res

1 − α

which has real solutions only for 0 < 1 − α

<β

and, checking against the

exact (6.79), we see that we must add to this the condition β

< 1. Rewriting these