Boyd T.J.M., Sanderson J.J. The Physics of Plasmas

Подождите немного. Документ загружается.

Waves in unbounded homogeneous plasmas

6.1 Introduction

Historically studies of wave propagation in plasmas have provided one of the

keystones in the development of plasma physics and they remain a focus in con-

temporary research. Much was already known about plasma waves long before the

subject itself had any standing, early studies being prompted by practical concerns.

The need to allow for the effect of the geomagnetic ﬁeld in determining propagation

characteristics of radio waves led to the development, by Hartree in 1931, of what

has become known as Appleton–Hartree theory. About the same time another basic

plasma mode, electron plasma oscillations, had been identiﬁed. In 1926 Penning

suggested that oscillations of electrons in a gas discharge could account for the

anomalously rapid scattering of electron beams, observed over distances much

shorter than a collisional mean free path. These oscillations were studied in detail

by Langmuir and were identiﬁed theoretically by Tonks and Langmuir in 1928.

Alfv

en’s pioneering work in the development of magnetohydrodynamics led

him to the realization in 1942 that magnetic ﬁeld lines, pictured as elastic strings

under tension, should support a class of magnetohydrodynamic waves. The shear

Alfv

en wave, identiﬁed in Section 4.8, ﬁrst appeared in Alfv

en’s work on cosmical

electrodynamics. Following the development of space physics we now know that

Alfv

en (and other) waves pervade the whole range of plasmas in space from the

Earth’s ionosphere and magnetosphere to the solar wind and the Earth’s bow shock

and beyond.

There is a bewildering collection of plasma waves and schemes for classifying

the various modes are called for. Plasma waves whether in laboratory plasmas or

in space are in general non-linear features. Moreover, real plasmas are at the same

time inhomogeneous and anisotropic, dissipative and dispersive. To avoid being

overwhelmed by detail at the outset some radical simpliﬁcations are needed and

so we begin by assuming that the medium is unbounded and consider only small

197

198 Waves in unbounded homogeneous plasmas

disturbances so that a linear theory of wave propagation is adequate. Even this

is a tall order and to begin with we make a further approximation and ignore the

effects of plasma pressure. This allows us to discuss a number of electromagnetic

modes in some detail since thermal effects play only a minor role in their dispersion

characteristics. To make matters even more straightforward we move towards a

general dispersion relation in stages, ﬁrst identifying modes that propagate along,

and transverse to, the magnetic ﬁeld before dealing with oblique propagation. In

all of this we are helped by the natural ordering of the electron and ion masses in

separating modes into high and low frequency regimes. This ordering underpins a

classiﬁcation of dispersion characteristics in terms of wave normal surfaces which

is discussed in outline for a cold plasma.

Dropping the cold plasma approximation and allowing for plasma pressure en-

ables us to identify other waves, in particular electrostatic modes. Thermal ef-

fects bring dissipation, not usually via inter-particle collisions, though these may

contribute particularly in partially ionized plasmas. In most plasmas of interest,

interactions between plasma electrons and ions and the waves themselves are more

important. Moreover, since these wave–particle interactions generally involve only

those particles with thermal velocities close to the phase velocity of the wave they

cannot be dealt with using a ﬂuid model. Thus the discussion of the most important

of these interactions, Landau damping, has to await the development of kinetic

theory in Chapter 7.

6.2 Some basic wave concepts

Before embarking on a description of the propagation characteristics of small am-

plitude waves in plasmas we review brieﬂy some basic wave concepts, familiar

from the theory of electromagnetic wave propagation. We restrict our discussion to

plane wave solutions of the wave equation, a plane wave being one for which the

wave disturbance is constant over all points of a plane normal to the direction of

propagation of the wave. For the plane wave solutions

E(r, t) = E

exp i(k · r − ωt) B(r, t) = B

exp i(k · r − ωt)

the vacuum divergence equations demand that k ·E

= 0 = k ·B

so that (E, B, k)

form a triad of orthogonal vectors.

The electric ﬁeld in a plane wave is expressed in general by a superposition of

two linearly independent solutions of the wave equation. Choosing the z-axis along

the wave vector k gives

E(z, t) = (E

x + E

y) exp i(kz − ωt ) (6.1)

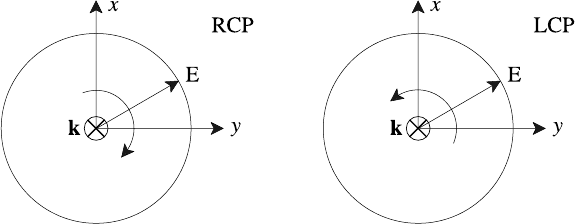
6.2 Some basic wave concepts 199

Fig. 6.1. Circularly polarized plane waves.

in which E

, E

are complex amplitudes

= E

exp(iα) E

= E

exp(iβ)

where E

, E

are real. With δ = β − α, (6.1) becomes

E(z, t) =



x + E

iδ



exp i(kz − ωt + α) (6.2)

At each point in space the electric vector rotates in a plane normal to

z and as time

evolves its tip describes an ellipse. This is most easily seen by setting δ =±π/2

so that

E(z, t) = (E

x ± iE

y) exp i(kz − ωt + α)

from which

(z, t) = E

cos(kz − ωt + α)

(z, t) =∓E

sin(kz − ωt + α)

(

(6.3)

Thus in general an electromagnetic wave is elliptically polarized. In the special

case when E

or E

= 0 the electric ﬁeld is linearly (or plane) polarized, while

if E

= E

the ﬁeld is circularly polarized.

To an observer looking along the direction of propagation the negative sign in

(6.3) corresponds to an electric ﬁeld vector, at any point z, rotating in a clockwise

direction. In this case, for E

= E

the wave is said to be right-circularly

polarized (RCP). For the positive sign, rotation is anticlockwise and the wave is

left-circularly polarized (LCP). Both polarizations are illustrated in Fig. 6.1.

With δ =±π/2 and deﬁning the wave polarization in terms of the complex

amplitudes in (6.2) by

P = iE

we see that P > 0(< 0) represents clockwise (anticlockwise) rotation and P =

+1(−1) indicates RCP(LCP).

200 Waves in unbounded homogeneous plasmas

6.2.1 Energy ﬂux

Deﬁning the Poynting vector S = E × H allows us to describe the ﬂux of energy

associated with electromagnetic ﬁelds. Poynting’s theorem is an expression of the

electromagnetic energy ﬂux as a balance between the rate of change of energy in

the elecromagnetic ﬁeld, with energy density W =

(

E · D + B · H

)

, and power

dissipated ohmically in the system, j · E. Then at any instant

∂W

∂t

+ ∇ · S =−j · E (6.4)

With harmonic time dependence, the time-averaged energy ﬂux becomes

S=

(E × H

∗

) (6.5)

The time-average of ∂ W/∂t vanishes, leaving, for sources contained in a volume

V bounded by a closed surface σ with unit normal vector n,



S·n dσ =−





E · j

∗

dV (6.6)

For a dissipation-free system E · j vanishes and so there is no net energy ﬂux

averaged over a cycle.

6.2.2 Dispersive media

So far we have considered only monochromatic waves. In practice even with such

a monochromatic source as a laser there will be a spread in frequency ω and

wavenumber k. Moreover in general ω = ω(k) so that a wave-form that is not

monochromatic will change as it propagates, exhibiting dispersion. Consider, for

example, scalar waves propagating along the z-axis; using a Fourier representation

E(z, t) =

√

(2π)



∞

−∞

a(k) exp[i(kz − ω(k)t)]dk (6.7)

and ω = ω(k) is known as the dispersion relation. Equation (6.7) and

a(k) =

√

(2π)



∞

−∞

E(z, 0)e

−ikz

deﬁne a wave packet. Assume, for convenience, that a(k) is peaked about some

wavenumber k

. The central question is this: ‘Given a particular wave packet at

t = 0 (the pulse shape), what does it look like at some later time?’ Provided the

medium is not too dispersive, ω(k) may be expanded about k

ω(k) = ω



dω



k=k

(k − k

) +···

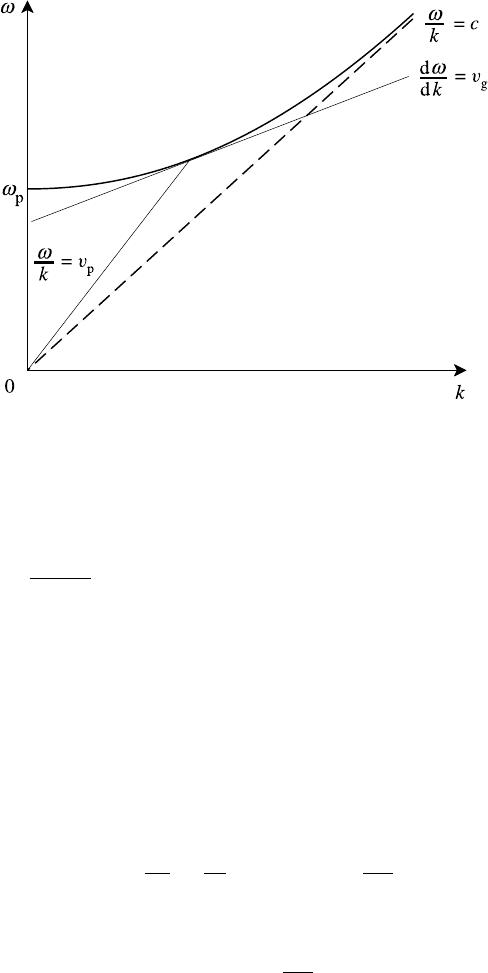
6.2 Some basic wave concepts 201

Fig. 6.2. Dispersion curve for electromagnetic wave.

where ω

stands for ω(k

) and so

E(z, t) =

√

(2π)



∞

−∞

a(k) exp{i[kz − ω

t − (dω/dk)

(k − k

)t]}dk

Then

E(z, t)  E(z − v

t, 0) exp[i(k

− ω

)t] (6.8)

which represents a pulse travelling without distortion with a velocity v

(dω/dk)

k=k

. This is the group velocity. The group velocity appears in this con-

text as the propagation velocity of a wave packet, a concept ﬁrst introduced by

Hamilton.

To relate v

to the phase velocity v

= ω/k is straightforward:

dω

(kv

) = v

+ k

or equivalently in terms of the wavelength

= v

− λ

dλ

Clearly, when the phase velocity is independent of wavelength there is no disper-

sion. Such is the case for the shear Alfv

en wave introduced in Section 4.8. For

/dλ>0, v

and the wave is said to exhibit normal dispersion. An electro-

magnetic wave propagating in a plasma provides an example of normal dispersion

202 Waves in unbounded homogeneous plasmas

since its dispersion relation (obtained in Section 6.3.1) is ω

= ω

+ k

, which

means that dω/dk = kc

/ω = c

. Since v

= ω/k > c, it follows that v

< c

as shown in Fig. 6.2.

6.3 Waves in cold plasmas

As discussed in Section 3.5, a cold plasma is one in which the thermal speeds of

the particles are much smaller than the phase speeds of the waves and the cold

plasma wave equations, given in Table 3.4, are simply the ion and electron equa-

tions of continuity and motion in the electromagnetic ﬁelds, which are governed

by Maxwell’s equations.

Since we shall discuss only small amplitude waves we shall be concerned with

the linearized version of the cold plasma equations, namely

∂n

∂t

+ ∇ · (n

) = 0 (6.9)

∂u

∂t

+ u

× B

) (6.10)

∇ × E

=−

∂B

∂t

(6.11)

∇ × B

−

∂E

∂t

= µ

j = µ



(6.12)

∇ · E



(6.13)

∇ · B

= 0 (6.14)

where the species label has been suppressed but the sums in (6.12) and (6.13) are

over species and

n = n

+ n

u = u

E = E

B = B

+ B











(6.15)

with the quantities n

and B

being constant in time and space. Thus, the lin-

earization describes a small departure from a plasma in equilibrium. The closed

set of two-ﬂuid wave equations is actually (6.9)–(6.12) (remembering that (6.9)

and (6.10) must be written for ions and electrons), since (6.13) and (6.14) are

essentially initial conditions; if they are satisﬁed at some time t

, we can show

that they must be satisﬁed at all other times.

In the usual way we eliminate B

from (6.11) and (6.12) to get

∇ × ∇ × E

=−

∂

∂t

− µ

∂j

∂t

(6.16)

6.3 Waves in cold plasmas 203

Next, using the second equality in (6.12) and solving (6.10) for u

, we obtain j in

terms of E

which we may express formally as

j = σ · E

(6.17)

where σ is the conductivity tensor. Then, assuming all variables vary like

exp i(k · r − ωt), (6.16) becomes

n × (n × E

) =−E

−

σ · E

=−ε · E

(6.18)

where n = ck/ω is a dimensionless wave propagation vector and ε is the cold

plasma dielectric tensor. The requirement that this equation should have a non-

trivial solution yields the dispersion relation containing all the information about

linear wave propagation in a cold plasma.

To ﬁnd the elements of σ (and hence ε) we must solve (6.10), the components

of which, dropping the subscript 1 and writing  = eB

/m,are

−iωu

− u

= eE

/m (6.19)

−iωu

+ u

= eE

/m (6.20)

−iωu

= eE

/m (6.21)

and then substitute the results in the expression for j in (6.12). This is straight-

forward but we can minimize the computation involved by ﬁrst carrying out the

calculation for the variables,

E, ˜



with components

= u

± iu

, u

= E

± iE

, E



= 

± i 

,







(6.22)

since the conductivity tensor ˜σ, deﬁned by



=˜σ ·

E (6.23)

is diagonal. By combining (6.19) and (6.20) in obvious ways we get the solutions

ieE

m(ω ∓ )

, u

ieE

mω

(6.24)

and substituting in





0α

u (6.25)

204 Waves in unbounded homogeneous plasmas

we see, by comparison with (6.23), that

˜σ = iε









pα

ω − 



pα

ω + 



pα







(6.26)

Now from (6.22) it follows that the matrix that transforms u, E and j to

E, ˜



T =





1 i 0

1 −i 0

001





and its inverse

−1





1/21/20

−i/2 i/20

001





Thus, from (6.23) we obtain

j = T

−1

·˜



= T

−1

·˜σ · T · E

and, comparing with (6.17), we see that

σ = T

−1

·˜σ · T

giving

σ =





( ˜σ

+˜σ

)/2 i( ˜σ

−˜σ

)/20

−i( ˜σ

−˜σ

)/2 ( ˜σ

+˜σ

)/20

00˜σ





(6.27)

where the components of ˜σ are as in (6.26).

Now, returning to (6.18), we may write the dielectric tensor components

= δ

+ (i/ε

ω)σ

, that is

ε =





S −iD 0

iD S 0

00P





(6.28)

6.3 Waves in cold plasmas 205

where

S =

(R + L) = 1 −

(ω

+ 



)

(ω

− 

)(ω

− 

)

D =

(R − L) =

ω(

+ 

)

(ω

− 

)(ω

− 

)

R = 1 −

(ω + 

)(ω + 

)

L = 1 −

(ω − 

)(ω − 

)

P = 1 −











(6.29)

and ω

= ω

+ω

is the square of the plasma frequency. Note that, in combining

the elements ˜σ

±˜σ

, we have used the fact that ω



+ ω



= Ze

−

)/m

= 0 because of equilibrium charge neutrality.

Finally, without loss of generality, we may choose axes such that n =

(n sin θ,0, n cos θ), as shown in Fig. 6.3, so that (6.18) may be written

(n · E)n − n

E + ε · E = 0

and hence





S − n

cos

θ −iD n

cos θ sin θ

iD S− n

cos θ sin θ 0 P − n

sin













= 0 (6.30)

Thus, taking the determinant of the coefﬁcients, the general dispersion relation for

cold plasma waves is

− Bn

+ C = 0 (6.31)

where

A = S sin

θ + P cos

B = RL sin

θ + PS(1 + cos

θ)

C = PRL







(6.32)

We treat this as an equation to be solved for n

as a function of θ, the angle of prop-

agation relative to the magnetic ﬁeld B

; the dimensionless quantities ω

/ω, 

/ω,



/ω, occurring in the coefﬁcients (see (6.29)), are to be regarded as parameters

which vary according to choice of wave frequency and equilibrium plasma.

206 Waves in unbounded homogeneous plasmas

Fig. 6.3. Orientation of wave propagation vector relative to magnetic ﬁeld.

Since a general discussion of the solutions of (6.31) is algebraically challenging,

our approach will be to look initially at waves propagating parallel (θ = 0) and

perpendicular (θ = π/2) to the magnetic ﬁeld. To this end a useful alternative

expression of (6.31) is obtained by solving it for tan

θ as a function of n

with the

result

tan

θ =−

P(n

− R)(n

− L)

(Sn

− RL)(n

− P)

(6.33)

There can be only real solutions of (6.31) for n

since in the cold, non-streaming,

plasma equations there are no sources of free energy to drive instabilities and no

dissipation terms to produce decaying waves and it is a simple matter to prove

this formally by showing that the discriminant of the bi-quadratic equation may be

written in the form

− 4AC = (RL − PS)

sin

θ + 4P

cos

θ ≥ 0 (6.34)

Thus, n is either pure real or pure imaginary corresponding to wave propagation

or evanescence, respectively. The changeover from propagation to evanescence (or

vice versa) takes place whenever n

passes through zero or inﬁnity. From (6.31)

and (6.32), it is clear that the ﬁrst of these possibilities occurs whenever C = 0,