Boyd T.J.M., Sanderson J.J. The Physics of Plasmas

Подождите немного. Документ загружается.

5.4 Magnetic ﬁeld generation 167

Ω

equatorial

plane

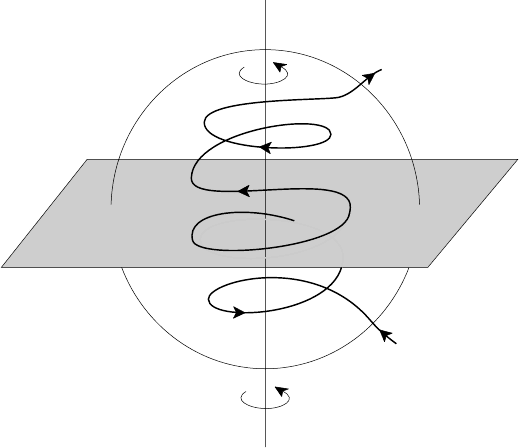
Fig. 5.16. Illustration of -effect (after Moffat (1993)).

the kinetic helicity ω · u =−ku

is constant. Now it turns out that such a ﬂow

can deform a straight magnetic ﬁeld line into a helix, as indicated in Fig. 5.17(b),

though the way in which this is done is quite subtle and requires ﬁnite resistivity.

We have seen already in Section 4.3.4 that a current density parallel to the

magnetic ﬁeld produces a helical ﬁeld. However, the electromotive force u × B,

resulting from the interaction of ﬂow and ﬁeld, gives rise to a current component

perpendicular to B in ideal MHD and it is only when the effect of ﬁnite resistivity

shifts the phase of the magnetic ﬁeld perturbation b relative to u that a space-

averaged u × b leads to a current component parallel to B, i.e. j = αB; the

constant α is proportional to the phase shift which, in turn, is proportional to the

resistivity. Steenbeck, Krause and R

adler (1966) showed that the α-effect occurs in

any turbulent ﬂow ﬁeld provided that the mean helicity ω · u = 0.

In toroidal geometry the x-axis transforms to the toroidal direction and we see

that the α-effect produces a poloidal component B

from a toroidal ﬁeld B

. Thus,

the combined α-mechanism comprises a regenerative cycle. It is now widely

accepted that it is by this cycle that the magnetic ﬁelds of the Earth and Sun are

maintained and there is a nice irony in that the very effect (ﬁnite resistivity) that

makes a regenerative mechanism necessary is also essential to its operation.

Although the kinematic problem is generally well understood the dynamic prob-

lem is still wide open. In both the Earth and Sun the α-mechanism operates in

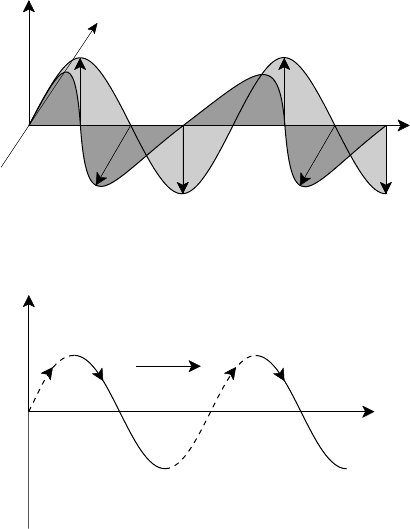
168 Resistive magnetohydrodynamics

Bj =

(a)

(b)

Fig. 5.17. Illustration of α-effect (after Moffat (1993)).

a convection zone which is a spherical annulus. For the Earth this is the liquid

outer core which lies between the solid inner core and the Earth’s mantle. The

most widely accepted model is one originally proposed by Braginsky (1991) who

suggested that the slow solidiﬁcation of the liquid at the inner core boundary

(ICB) releases an excess of lighter elements, such as sulphur, in the liquid alloy

of the outer core. The buoyancy of the lighter ﬂuid causes it to rise towards the

core–mantle boundary (CMB) generating convection currents as it does so. Beyond

that, however, essential questions regarding the length scale of the rising elements,

the degree of turbulence that they generate and the rate at which they mix with the

heavier liquid, which determines the diffusion rate, remain unanswered. The thrust

of research is therefore, on the experimental side, a detailed study of the variation

with time of the Earth’s ﬁeld so that, by the application of inverse theory, the ﬁeld

at the CMB may be reconstructed and, on the theoretical side, the development of

self-consistent models.

A computer simulation by Glatzmaier and Roberts (1995) which simulated the

Earth’s ﬁeld over a period of 40 000 years produced the ﬁrst convincing evidence

5.5 The solar wind 169

that ﬂuid motions in the Earth’s core could sustain the geomagnetic ﬁeld. The

three-dimensional model has not only generated a stable, dipole ﬁeld over a period

roughly three times the magnetic diffusion time (∼13 000 years) but one which

reproduced other geomagnetic features such as magnetic axis displacement (from

rotational axis) and ﬁeld reversal.

5.5 The solar wind

The continual streaming of plasma from the Sun’s surface is known as the solar

wind and we have noted already that there are important consequences for the

geomagnetic ﬁeld arising from reconnection in the region where the solar wind

strikes the magnetosphere. The solar wind extends the solar plasma to the Earth and

well beyond; in fact, the solar wind is thought to continue to a boundary with the

interstellar medium at 50–100 AU. Correlation between variations of the Earth’s

magnetic ﬁeld and activity on the Sun had been observed since the nineteenth

century but attempts to explain the connection on the basis of static models of the

solar corona failed to provide satisfactory solutions and, although there had been

earlier suggestions that plasma ejected from the Sun was the cause of geomagnetic

storms and the shape of comet tails, it was not until 1958 that Parker established

the theoretical basis for the solar wind by solving the steady ﬂow problem. Soon

afterwards satellite observations conﬁrmed its existence and began to compile its

physical properties in ever increasing detail.

Parker (1958) showed that no hydrostatic equilibrium between the solar corona

and interstellar space was possible and that non-equilibrium is what gives rise to

a supersonic low density ﬂow which is the solar wind. Although both the high

temperature of the corona and the outﬂowing solar wind have been long observed,

the precise mechanism that leads to plasma ﬂowing out from the Sun’s surface

is not well understood. The slowest ﬂows can be attributed to a thermally driven

wind but non-thermal additions are needed in the supersonic region. Energy and

momentum transfer from hydromagnetic waves, such as Alfv

en waves, are likely

sources and Alfv

en-like ﬂuctuations have been observed in the solar wind. Param-

eters characteristic of the solar wind are given in Table 5.3 at distances of a solar

radius (R



= 6.96 × 10

m) and at 1 AU = 215R



The solar wind is composed largely of protons and is permeated by a magnetic

ﬁeld. The magnetic ﬁeld is frozen in the radial ﬂow outwards from the surface.

However because of the Sun’s rotation the magnetic ﬁeld is twisted into a spiral.

It exhibits a complex structure attributable in part to the admixture of open and

closed magnetic structures at the Sun’s surface. In a general sense open magnetic

structures are favourable to the generation of the solar wind while closed structures

oppose it.

170 Resistive magnetohydrodynamics

Table 5.3. Solar wind characteristics

r/R



1 215

Composition H

,He

Number density n

−3

) 2 ·10

7 · 10

Ion temperature T

(K) 10

Plasma ﬂow velocity u (km s

−1

) 1 400

Magnetic ﬁeld B (nT) 10

The ﬂow problem that Parker solved was hydrodynamic rather than hydromag-

netic in that he assumed that the dominant forces in the equation of motion are the

pressure gradient and gravity. Thus, for the steady, spherically symmetric ﬂow of

an isothermal plasma the equation of motion is

ρu

=−

−



(5.28)

where G is the gravitational constant and M



is the mass of the Sun. Mass conser-

vation requires

4πr

ρu = const. (5.29)

and the assumption of constant temperature means that we can deﬁne a constant

isothermal sound speed by

= P/ρ. (5.30)

Differentiating (5.29) and (5.30) and eliminating dρ/dr gives dP/dr in terms of

du/dr which may be substituted in (5.28) to give



u −



−



(5.31)

This equation has a critical point at r = r

≡ GM



/2u

, u = u

, where du/dr is

undeﬁned. Its analytic solution is





− log





= 4 log





+ C (5.32)

where C is a constant of integration. The solution curves are sketched in Fig. 5.18;

the critical point A at (r

, u

) is a saddle point with du/dr becoming inﬁnite as

u → u

(r = r

) and vanishing as r → r

(u = u

), in accordance with (5.31).

The trajectories through the critical point separate the various classes of solution.

Of these I and III are double-valued and, therefore, physically unacceptable while II

and IV have solar wind speeds which are entirely supersonic (II) or subsonic (IV),

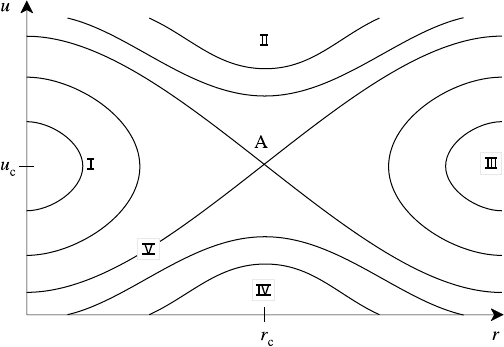
5.5 The solar wind 171

Fig. 5.18. Solution curves for Parker’s solar wind model.

neither of which accords with observation. Since the solar wind has a ﬂow speed

which is subsonic at the Sun and supersonic at the Earth the only acceptable so-

lution is the (positive slope) trajectory (V) through the critical point (r

, u

). It is

apparent from (5.32) that C =−3 for this curve.

For r →∞, u  u

so that u ∼ (log r)

1/2

and, from (5.29) and (5.30), P ∼ ρ ∼

−2

(log r)

−1/2

→ 0, as one would expect. The model predicts a ﬂow speed of about

10 km s

−1

at the Sun and about 100 km s

−1

at the Earth, both of which are of the

right order of magnitude. Unfortunately, its prediction for the density at the Earth

is two orders of magnitude too high. Consequently, there have been many further

developments of the model. In particular, the assumption of an isothermal plasma is

known to be an over-simpliﬁcation so the model has been extended to include heat

conduction in an energy equation and, in a further reﬁnement, a two-ﬂuid model

with separate ion and electron energy equations has been investigated since energy

exchange between the species is negligible in the solar wind except for the region

very close to the Sun. We shall not pursue these developments but an account of

them may be found in Priest (1987).

Of course, a major simpliﬁcation of Parker’s model is the omission of the mag-

netic ﬁeld. If the magnetic energy in the solar wind is negligible compared with its

kinetic energy, as Parker assumed, then the ﬁeld does not signiﬁcantly affect the

ﬂow but, on the other hand, the ﬂow drags the ﬁeld lines out from the solar surface

as indicated in Fig. 5.19. In plan view, looking down the polar axis, the ﬁeld lines

are spirals due to the combined effect of the solar wind and solar rotation. We can

calculate the angle ψ(r) between the ﬂow velocity u(r)

r and the magnetic ﬁeld

B(r) by considering the motion of a ﬂuid element which leaves a point P

on the

172 Resistive magnetohydrodynamics

Fig. 5.19. Field lines at solar surface.

Sun’s surface at time t = 0. To an observer at P

(t) rotating with the Sun, the ﬂuid

element traces out the spiral path P

(t) → P(t) shown in Fig. 5.20 and, in the

ideal MHD approximation, this must be a ﬁeld line since there can be no motion

perpendicular to the ﬁeld lines. On the other hand, to an observer not rotating with

the Sun but remaining at P

(0) the path of the ﬂuid element is straight and radial, a

motion that is made possible by the rotation of the ﬁeld line about P

. In plane polar

coordinates with origin at P

(0) the velocities of ﬂuid element and ﬁeld line at P(t)

are u = [u(r), 0] and v

= [0,(r − R



)], respectively. Then the condition that

there should be no motion of the ﬂuid element perpendicular to the ﬁeld line is

u sin ψ(r ) = v

cos ψ(r)

from which we get

tan ψ(r) =

(r − R



)

u(r)

(5.33)

At the Earth this angle is about π/4.

In fact, the assumption that the kinetic energy dominates the magnetic energy, so

that the ﬁeld does not affect the ﬂow, does not hold very close to the Sun’s surface

and the ﬁeld lines wind up into a very tight spiral slowing the radial ﬂow drastically

at low latitudes. The radius r

at which the kinetic and magnetic energies are equal,

i.e. the ﬂow speed is the Alfv

en speed v

, is called the Alfv

en radius.Forr  r

the ﬁeld keeps the solar wind rotating with the Sun thereby increasing its angular

momentum (at the expense of the Sun! – this effect is thought to have slowed the

Sun’s rotation signiﬁcantly during its lifetime); well beyond r = r

the effect of the

ﬁeld on the wind becomes negligible and it continues its outward ﬂow conserving

5.5 The solar wind 173

r(t)

u(r)

B(r)

Ω

P(t)

(t)

(0)

Fig. 5.20. Plasma motion in solar wind.

its angular momentum. In a more accurate model, therefore, the solar wind has a

ﬂow velocity with both radial and azimuthal components.

The azimuthal component of the ﬂow velocity of the solar wind in the equatorial

plane of the Sun was calculated by Weber and Davis (1967). They examined a

steady state model with axial symmetry in which the ﬁeld lines are completely

drawn out by the solar wind in the equatorial plane so that there is no component of

the ﬁeld perpendicular to the plane. Thus, in the equatorial plane it is assumed that,

in spherical polar coordinates, B = [B

(r), 0, B

(r)] and u = [u

(r), 0, u

(r)].

Assuming that the ﬁeld is radial at the solar surface (r = R



), i.e. B(R



) =

, 0, 0) say, it follows from ∇ · B = 0 that

(r) = B



(5.34)

Mass conservation requires

ρu

= const. (5.35)

174 Resistive magnetohydrodynamics

and the steady state induction equation, ∇ × (u × B) = 0, gives



r(u

− u

)



= 0

which may be integrated to obtain

− u

=−R



/r (5.36)

assuming u



) = R



. It then follows from (5.34) and (5.36) that

(r) =

(r) − r 

(r)

(r) (5.37)

The equation of motion is

ρ(u · ∇)u =−∇ P + (∇ × B) × B/µ

− (GM



ρ/r

)r (5.38)

the φ-component of which is simply

(ru

) =

(rB

) (5.39)

But from (5.34) and (5.35), ρu

and B

are both constant so multiplying (5.39)

by r

we may integrate to get

−

ρu

= const. = L (5.40)

say. Introducing the radial Alfv

en Mach number

≡

/(µ

ρ)

1/2

(5.41)

we may substitute (5.37) in (5.40) to obtain

(r) = r(M

L/(r

) − 1)/(M

− 1) (5.42)

This equation determines u

as a function of r and M

(r). From observations

it is known that M

 1 near the surface of the Sun and that M

 10 at the

Earth. The point r = r

, between the Sun and the Earth, at which M

= 1 is called

the Alfv

en critical point. At this point the numerator in (5.42) must vanish to keep

) ﬁnite so that L = r

From (5.34), (5.35) and (5.41) we deduce that M

is a constant, which we

evaluate at the Alfv

en critical point to get

(5.43)

5.5 The solar wind 175

0 50 100 150 200

250

(km s

–

)

–

)

(

Ω

Asymptotic solution

Fig. 5.21. Azimuthal ﬂow velocity of solar wind (after Weber and Davies (1967)).

so that we may write (5.42) as

(r) = r

(1 − u

)

(1 − M

)

(5.44)

and (5.37) as

(r) =−B

r

(1 − (r/r

)

(1 − M

)

=−





(1 − (r/r

)

(1 − M

)

(5.45)

where we have also used (5.34). From these expressions we may obtain the asymp-

totic behaviour of the azimuthal components of u and B. First of all, for r →∞

the effect of the magnetic ﬁeld is negligible and from Parker’s solution we know

that u

∼ (log r)

1/2

so that from (5.43) we see that M

∼ r (log r)

1/4

and hence,

∼ r

−1

and B

∼ (r(log r)

1/2

)

−1

.Forr  r

, we obtain from (5.43)–(5.45), to

lowest order in u

and r/r

= r



1 −



1 −







=−B

r



1 −







1 −





The solution for u

obtained by Weber and Davis is shown in Fig. 5.21. The

176 Resistive magnetohydrodynamics

dashed line is the asymptotic solution

→

r



1 −



which follows from (5.44). If, in the simple model discussed above, the plasma,

constrained by the Sun’s magnetic ﬁeld, were to rotate with the angular velocity of

the Sun out to r = r

and then experience no effect of the ﬁeld for r > r

, conser-

vation of angular momentum would give u

→ ωr

/r. The factor (1 − v

)

represents a correction to this oversimpliﬁed picture on account of the angular

momentum retained by the magnetic ﬁeld at large r .

Weber and Davis go on to calculate u

from the radial component of (5.38) using

the adiabatic gas law for p

pρ

−γ

= const. = p

−γ

where p

and ρ

are the solar wind pressure and density at r = r

. The equation

requires numerical solution and we shall not pursue the details here. However, it is

of interest to note that the (u

, r) phase plane now has three critical points occurring

in succession at the slow magnetoacoustic, shear Alfv

en, and fast magnetoacoustic

wave speeds, i.e. at the characteristic wave speeds for an ideal plasma (see Sec-

tion 4.8). The ﬁrst of these is the equivalent of Parker’s critical point, occurring

at slightly below the sound speed c

. The second is, of course, the Alfv

en critical

point already mentioned, and the third follows it almost immediately because in

the solar wind β  1 so that the fast wave speed is only slightly greater than v

The only acceptable solutions are ones passing through all three critical points and,

of these, only one gives results of the right order of magnitude both at the Sun and

at the Earth; this solution gives results for u

and ρ which are essentially the same

as Parker’s solution. At the Earth the azimuthal speed is typically two orders of

magnitude smaller than the radial speed.

The most serious criticism of these calculations is that they are based on a

one-ﬂuid model. Since the average electron–ion mean free path in the solar wind

is of the order of 1 AU, only the ﬁelds bind electrons and ions together and at the

very least a two-ﬂuid model seems essential. Satellite observations have provided

very detailed information about ion and electron velocity distributions in the solar

wind and whereas ion distributions may, to ﬁrst order, be represented as drifting

Maxwellians, in which the drift velocity is much greater than the thermal speed,

this is not the case for the electrons. For electrons the drift velocity is very much

less than the thermal speed so the distribution is approximately isotropic and close

to a power law. As Bryant (1993) has pointed out, such a distribution has no

characteristic energy and therefore no meaningful temperature. A kinetic treatment

may therefore be essential for a satisfactory description of electron properties.