Boyd T.J.M., Sanderson J.J. The Physics of Plasmas

Подождите немного. Документ загружается.

5.2 Magnetic relaxation and reconnection 147

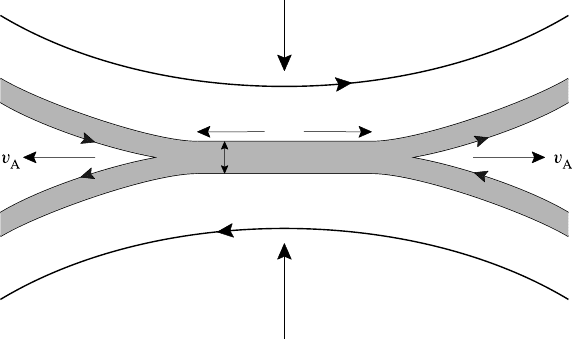
Fig. 5.4. Driven reconnection at X-type neutral point.

current sheet by the plasma ﬂow is balanced by the rate of ohmic dissipation so

that

u = η/2µ

d (5.4)

This equation combined with the expression of mass conservation gives

u = v

1/2

d = L/S

1/2

(5.5)

Identifying M

= u/v

= M

(the Alfv

en Mach number) as a dimensionless

index for the driven reconnection rate, it follows from (5.5) that M

= S

−1/2

From Table 5.1 we ﬁnd reconnection that is many orders of magnitude too slow

to characterize the evolution of solar ﬂares. By the same token an inverse aspect

ratio d/L ∼ 10

−6

implies a current sheet only metres thick for typical values of L,

which is unrealistic.

The realization that the Sweet–Parker reconnection rate was much too slow

pointed to the need for incorporating some faster mechanism into the current sheet

model. Petschek (1964) attempted to do this by means of a slow MHD shock model

which again involves a current sheet but leads to a reconnection rate now effectively

independent of resistivity. Petschek reasoned that the magnetic ﬁelds would meet

at a relatively narrow apex, rather than across the entire region envisaged in the

Sweet–Parker model and found a maximum reconnection rate

∼ (ln S)

−1

(5.6)

This weak dependence on resistivity seemed to ﬁt the bill and led to the model

being widely adopted despite a longstanding debate about its validity, over issues

148 Resistive magnetohydrodynamics

such as precisely how to deﬁne a Petschek regime and the boundary conditions

governing it. These misgivings were strengthened by insights gained from nu-

merical experiments on reconnection by Biskamp (1986). Biskamp (1993) has

given a detailed critique of the Petschek slow-shock model. On general grounds

Petschek’s model has been seen as counter-intuitive in that two plane regions of

highly conducting plasma with oppositely directed magnetic ﬁelds pushed together

might be expected to generate a ﬂat current sheet conﬁguration rather than the

cone required by the Petschek model. However Biskamp’s criticism centres on

the treatment of the diffusion region where a boundary layer solution, matching

the ideal MHD solution outside the diffusion zone to the resistive MHD solution

within, is required. Biskamp’s numerical experiments of driven reconnection do

not show a Petschek-like conﬁguration in the small η limit. Although features

characteristic of slow shocks are conﬁrmed by the simulations, Biskamp found

that as the reconnection rate increases, both the length and width of the diffusion

region increase, counter to Petschek’s predictions.

Whatever doubts persist over models for magnetic reconnection in solar ﬂares,

observations by Innes et al. (1997) have provided the ﬁrst direct evidence for

reconnection. They report ultraviolet observations of explosive events in the so-

lar chromosphere which point to the presence of oppositely directed plasma jets

ejected from small sites above the solar surface. Observations of these jets show

signs of some anisotropy in that jets directed away from the solar surface may

stream freely up to the corona while downward jets should suffer attenuation on

account of the increasing density of the chromosphere. The stream exhibiting a

blue shift, indicative of plasma ﬂowing away from the solar surface, is of very

much greater extent than the red stream.

5.3 Resistive instabilities

The ability of a plasma, through magnetic reconnection, to reach lower energy

states means that ideal MHD stability theory needs re-examination. Modiﬁcation

of the theory by the introduction of a small but ﬁnite resistivity leads to the dis-

covery of new instabilities. These resistive instabilities were ﬁrst derived in the

seminal paper of Furth, Killeen and Rosenbluth (1963). In this paper the resistive

MHD equations were solved in the boundary layer in which S  1 and ﬁeld line

diffusion takes place; the ideal MHD equations were solved outside this region

and the solutions matched at the boundary. Three instabilities were discovered

with growth times much smaller than τ

but much greater than τ

. One of these,

the tearing instability, arises spontaneously while the others are driven instabili-

ties.

5.3 Resistive instabilities 149

(y)

Fig. 5.5. Coordinate axes for calculation of resistive instabilities.

A discussion of the original calculation may be found in Miyamoto (1989) and

accounts of both the linear and non-linear theory of resistive instabilities have been

given by Bateman (1978) and by White (1983). In what follows we make no at-

tempt to repeat details of the full calculation in the original paper but derive instead

the basic equations from which the linear dispersion relation is obtained and, in

the spirit of Wesson (1981), use heuristic arguments to determine the parametric

dependence of the linear growth rates.

The procedure followed is close to that used in Chapter 4, in discussing linear

stability in ideal MHD, ﬁrst obtaining (4.67) and then (4.111) for the Rayleigh–

Taylor instability. We use the geometry illustrated in Fig. 5.5 and again assume

that equilibrium quantities vary only in the y direction. Incompressibility is also

assumed so that (4.107) holds. This is justiﬁed since the growth rates of the resistive

instabilities are very small on the hydromagnetic time scale τ

and this means that

ﬂuid and magnetic pressure changes tend to be compensating, having a negligible

effect on the dynamics of the instabilities. Two generalizations of the assumptions

used to derive (4.111) are required. However, one of these, the replacement of the

ideal by the resistive equation for P, turns out to be of no consequence since we

shall eliminate the ∇P term.

The other generalization is important since it introduces the driving term for one

of the resistive instabilities. We want to allow for variable resistivity in which case,

following the usual derivation of the induction equation from the Maxwell equation

150 Resistive magnetohydrodynamics

and Ohm’s law, we get

∂B

∂t

=−∇ × E

= ∇ × (u × B) − ∇ ×



∇ × B



= ∇ × (u × B) +

∇

B − ∇η ×

(∇ × B)

(5.7)

Since we are now treating η as a variable we need an extra equation to determine

it and for this we assume that it does not change within the ﬂuid element but only

on account of its advection so that

Dη

∂η

∂t

+ u · ∇η = 0 (5.8)

Linearizing (5.7) and (5.8) we have

∂B

∂t

= ∇ × (u

× B

) +

∇

− ∇η

(∇ × B

)

− ∇η

(∇ × B

)

(5.9)

and

∂η

∂t

=−u

· ∇η

(5.10)

Integrating (5.10) gives

=−ξ



(y) (5.11)

where we have used (4.64) and the prime denotes differentiation with respect to y.

Now substituting (5.11) in (5.9), the y component is

∂ B

∂t

= i(k ·B

∇

− i

(k · B

)



where we have dropped the subscript 1 on ﬁrst-order variables. Assuming, as in

our discussion of the Rayleigh–Taylor instability, that all variables are of the form

A(y)e

ikz+γ t

this equation may be integrated to obtain

= i(k ·B

)ξ



− k

) − i

(k · B

)



(5.12)

This is one of the basic equations from which the dispersion relation is obtained.

The second equation comes from the linearized equation of motion which is

∂u

∂t

=−∇ P

+ ρ

g +

(∇ × B

) × B

(∇ × B

) × B

(5.13)

5.3 Resistive instabilities 151

and the linearized continuity equation

∂ρ

∂t

=−u

· ∇ρ

(5.14)

where, since incompressibility is assumed, we have used ∇ · u

= 0. Integrating

(5.14) gives

=−ξ



and substituting this in (5.13) the y and z components are

=−

+ ξ



g −



+ B



+ B



+ B



− ikB

)] (5.15)

=−ikP



− ikB

) (5.16)

Now we use (4.107) for ξ

in (5.16) and substitute the resulting expression for

in (5.15) to get

[(ρ



)



− k

] + µ

gρ



+ B



+ B



+ B



− ikB

) − ik(B



− ikB

)



Also, since

∇ · B

= B



+ ikB

= 0

we may eliminate B

to obtain

[(ρ



)



− k

] + µ

gρ



= ikB





− k

−





= i(k · B

)





− k

−

(k · B

)



(k · B

)



(5.17)

which is the second basic equation relating ξ

and B

. It is easily veriﬁed that

putting η

≡ 0 in (5.12) and substituting B

= i (k · B

)ξ

in (5.17) reproduces

(4.111) with γ replacing iω.

5.3.1 Tearing instability

We begin our heuristic analysis of (5.12) and (5.17) by concentrating on the insta-

bility which arises by spontaneous reconnection of antiparallel ﬁeld lines. The role

of the η



term in (5.12), like that of the g term in (5.17), is to provide a driving force

for a resistive instability. For the moment let us drop both of these terms. Now, in

152 Resistive magnetohydrodynamics

the limit of vanishing resistivity we may ignore the diffusion term in (5.12) except

near the resonant surfaces where k · B

≈ 0 and we deﬁne the width  L of the

resistive boundary layer by equating the magnitudes of the convection and diffusion

terms in (5.12)

(k · B

)ξ

∼

∇

∼

γρ

(k · B

)



where the second approximation arises from (5.17). In this we have ignored the

variation (on scale length L) of equilibrium variables compared with the variation

(on scale length  L) of ﬁrst-order variables and we have assumed kL  1, i.e.

the wavelength of the perturbation is much greater than the width of the boundary

layer. Then replacing ξ



by ξ

/(L)

and (k·B

) by  Lk ·B



(0), since (k ·B

) = 0

at y = 0but(k ·B

)



= 0, we get

 L ∼



γη



)



1/4

(5.18)

Using (5.12) to eliminate ξ

from (5.17) it is clear that in the boundary layer we

have a fourth-order differential equation for B

whereas outside this region, where

the diffusion term is negligible, the equation reduces to second order. This is an

eigenvalue problem in which the eigenvalues, some of which lead to positive γ

and hence instability, are determined by matching the solutions at the boundaries

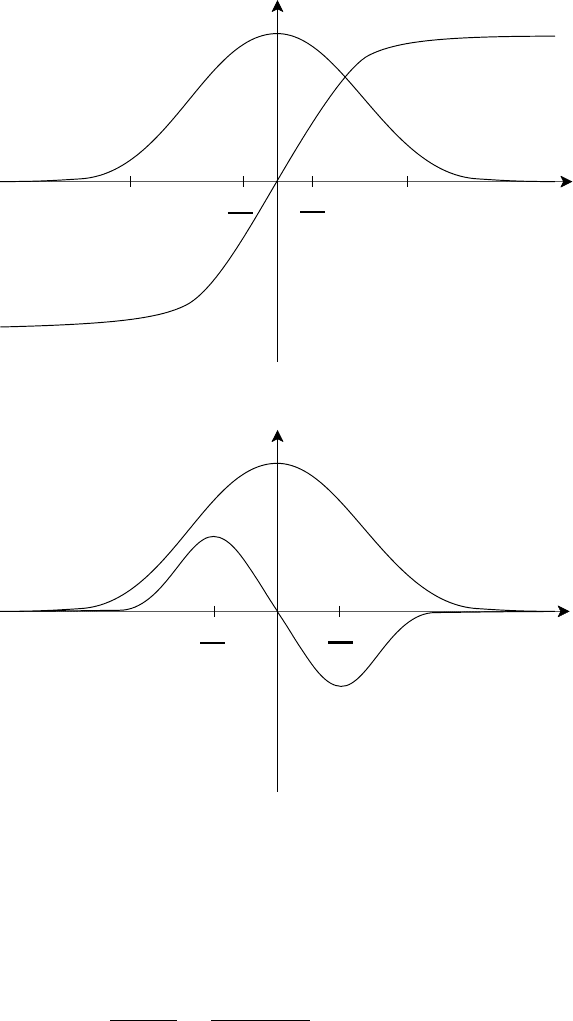
of the resistive region. Figure 5.6 shows schematically the variation of the key

quantities k · B

, (k · B

)



, B

and B



. The point to note is the rapid change in B



across the boundary layer which, on the scale L of the whole plasma, appears as

a discontinous change at the resonant surface (y = 0) and hence a very large B



The actual change is determined by the eigenvalue but we shall take it as given in

terms of a dimensionless quantity, usually denoted by 



, and deﬁned by





= lim

→0



( L/2) − B



(− L/2)

(0)

(5.19)

The same is true for ξ



so the dominant terms in (5.17) are those in ξ



and B



and

we may write

( L)

∼ (k ·B



∼ (k ·B

)



(L/2) − B



(− L/2)]

 L

∼ (k ·B

)

(0)



 L

(5.20)

5.3 Resistive instabilities 153

)

-1

′

Fig. 5.6. Characteristic variation in tearing instability.

in the limit  → 0 on using (5.19). Also, from (5.12), B

∼ (k ·B

)ξ

so that (5.20)

becomes

( L)

∼

(k · B

)





∼ k



)



L



and, substituting for  L from (5.18), we ﬁnd the parametric dependence of the

154 Resistive magnetohydrodynamics

> 0

< 0

k B

> 0

k B

< 0

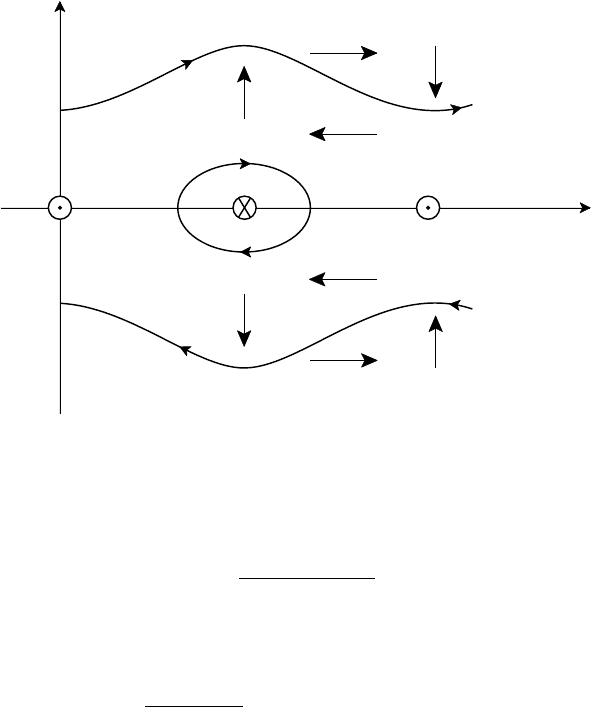
Fig. 5.7. Directions of current, ﬁeld and velocity variations in the tearing instability.

growth rate γ to be

γ ∼





)

(



)



1/5

(5.21)

In terms of the resistive diffusion and convection times τ

and τ

, this may be

written as

γ ∼



(kL)

(



)



1/5

∼ (kL)

2/5

(



)

4/5

−1

(5.22)

showing that the time scale for the development of this instability is two-ﬁfths

Alfv

enic (S/τ

)

2/5

and three-ﬁfths diffusive (1/τ

)

3/5

and thus intermediate be-

tween these widely differing time scales. In a tokamak τ

would be measured

typically in seconds, τ

in tens of nanoseconds and γ

−1

in milliseconds. This wide

separation of time scales justiﬁes the simple order of magnitude analysis we have

used.

The growth rate increases with resistivity, η, and with shear, (k ·B

)



. It is driven

by the Lorentz force which acts towards the resonant surface. Finite resistivity

allows ﬁeld lines to break and reconnect at the nodal X points and then contract

towards the axes of the magnetic islands passing through the O points. Figure 5.7

shows the directions of current, ﬁeld and velocity perturbations. Note that the

equilibrium current j

, maintaining the variation in B

(y), is in the x direction so

the growth of the instability increases the current at the O points and decreases it at

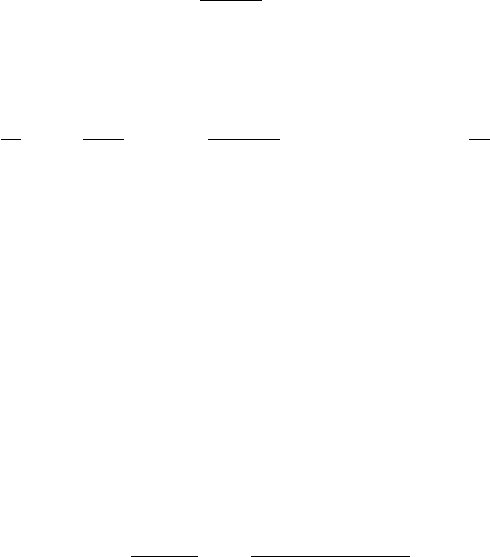
5.3 Resistive instabilities 155

the X points causing the current to break up into ﬁlaments. The characteristics of

this instability, namely the breaking of ﬁeld lines and ﬁlamentation of the current,

are reﬂected in the name given to it, i.e. the tearing mode.

Finally, an important feature of this instability is its dependence on 



, the

discontinuity in B



at the resonant surface. This means that the growth rate γ

is determined by the global state of the plasma and not by the local equilibrium

conditions at the resonant surface.

5.3.2 Driven resistive instabilities

Reintroduction of the η



term in (5.12) and the g term in (5.17) allows additional

possibilities for instability since these terms appear in the eigenvalues. To ﬁnd the

parametric dependence of the growth rates of these driven instabilities we need

only replace (5.20) by the corresponding approximations when the gravitational or

variable resistivity terms dominate the dynamics in the boundary layer.

In the case that the g term dominates we have

( L)

∼ k

gρ



which, on substitution from (5.18), leads to

γ ∼





1/3



kgρ





2/3

∼



(kL)



1/3

∼ (kL)

2/3





4/3

−1

(5.23)

where τ

= (ρ

/gρ



)

1/2

is a gravitational time scale. Keeping only the dominant

inertial and gravitational terms in (5.17), it is easily seen that ξ

grows when ρ



> 0

or g ·∇ρ

< 0, i.e. when there is an inverted density gradient as for the Rayleigh–

Taylor instability. This is the gravitational interchange mode. From (5.23) we see

that, unlike the tearing mode, this instability growth rate is reduced by increased

magnetic shear, and, since it depends on ρ



(0), it is a local instability. A similar

resistive interchange instability may occur in a curved magnetic ﬁeld when there is

a pressure gradient aligned with the curvature (see the discussion in Section 4.7.2).

Turning now to the third resistive instability, we ﬁrst substitute for (B



− k

)

from (5.12) in (5.17) to bring the η



term into the equation of motion and then

balance this term with the inertia term to obtain

(L)

∼

(k · B

)(k · B

)



156 Resistive magnetohydrodynamics

Table 5.2. Resistive instability characteristics

Mode Range γτ



Tearing kL < 1 (kL)

2/5

(



)

4/5

(kL)

−2/5

(



)

1/5

Gravitational g · ∇ρ

< 0 (kL)

2/3

(τ

/τ

)

4/3

(kL)

−1/3

(τ

/τ

)

1/3

interchange

Rippling η



= 0 (kL)

2/5

(Lη



/η

)

4/5

(kL)

−2/5

(Lη



/η

)

1/5

Hence,

γ ∼





)

(η



)



1/5

∼





Lη





(kL)



1/5

∼ (kL)

2/5

(Lη



/η

)

4/5

−1

(5.24)

As for the other driven instability, this is local. To understand its physical origin

we linearize Ohm’s law, assuming E = 0, to get

+ η

= u

× B

and substitute for η

from (5.11) so that

= ξ



+ u

× B

Thus, there is an additional (driving) force F

due to the η



term in j

,givenby

= ξ



× B

= (ξ · ∇η

)(j

× B

/η

)

Assuming the variation of η

(y) is monotonic across the resonant surface whilst B

changes sign, it follows that F

is stabilizing on one side and destabilizing on the

other. Physically, it is clear that F

is destabilizing on the side of lower resistivity

since this is where the current is increased. Thus, the ﬂuid motion is ampliﬁed only

on the lower resistivity side and this creates a rippling effect which gives the mode

its name. The motion of the plasma in relation to the ﬁeld lines for both driven

instabilities is illustrated in Fig. 5.8.

Table 5.2 lists the main parametric properties of the three resistive instabilities.

The tearing mode, because it is endemic and not dependent on an imposed driving

force and since its growth rate increases with magnetic shear, is usually the most

dangerous. Also, the other two are local instabilities with the resistive interchange

mode stabilized by shear and the rippling mode stabilized by high temperature

which increases the heat conductivity and invalidates the ‘adiabatic’ assumption

(5.8).