Boyd T.J.M., Sanderson J.J. The Physics of Plasmas

Подождите немного. Документ загружается.

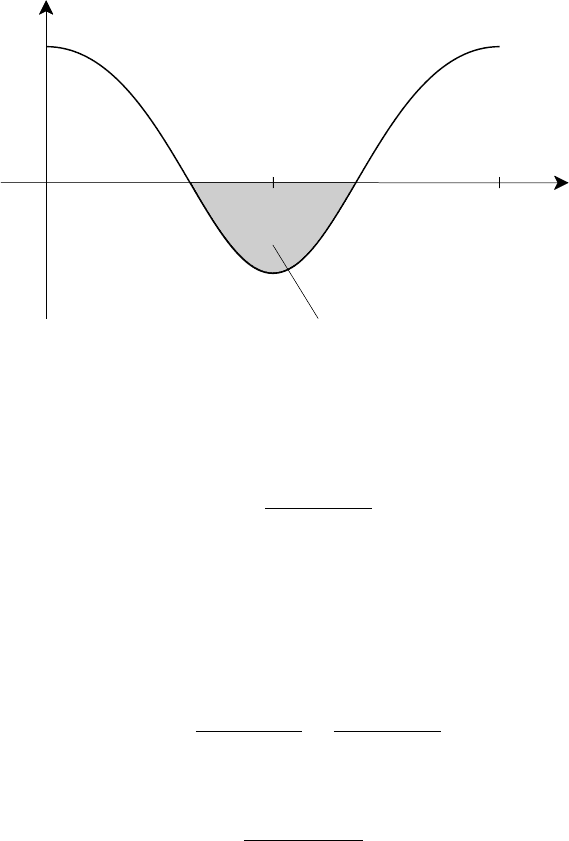
4.7 Interchange instabilities 127

unstable

Fig. 4.30. Schematic illustration of Rayleigh–Taylor instability zone for uniform magnetic

ﬁeld.

giving

=−

kg(ρ

− ρ

)

+ ρ

and conﬁrming that the equilibrium is unstable if the denser ﬂuid is above the less

dense, i.e. ρ

>ρ

. Clearly, the fastest growth rate (kg)

1/2

occurs when ρ

 ρ

We next demonstrate the stabilizing effect of a magnetic ﬁeld by supposing that

the ﬂuids are plasmas and that there is a uniform B

throughout. From (4.111) we

see that this simply replaces ρ

by ρ

− (k · B

)

/µ

to give

=−

kg(ρ

− ρ

)

+ ρ

2(k · B

)

(ρ

+ ρ

)

(4.112)

showing that shorter wavelength modes such that

k ≥

g(ρ

− ρ

)

cos

where θ is the angle between k and B

, are stabilized.

The same procedure (see Exercise 4.9) may be used to ﬁnd the dispersion

relation

=−kg + (k · B

)

/µ

(4.113)

for the case of an unmagnetized plasma of constant density ρ

supported by a

uniform magnetic ﬁeld B

. The qualitative features of both this result and (4.112)

are sketched in Fig. 4.30 for a given wavenumber k, showing that there is always

128 Ideal magnetohydrodynamics

an interval around θ = π/2 for which instability occurs. If, however, instead of a

uniform B

we have a rotating B

(y) then θ = θ(y) and the instability of a given

mode is restricted to a layer about the surface y = y

where k · B

) = 0. Thus,

the magnetic ﬁeld has two stabilizing roles. Any bending of the ﬁeld lines resists

the growth of the perturbation and magnetic shear limits the region of instability

when it occurs.

Surfaces where k ·B

= 0 play a crucial role in stability analysis quite generally

and are called resonant surfaces. In particular, we note that (4.111) has a singular

point wherever

− (k · B

)

/µ

= 0

Since (k · B

)

≥ 0, such singularities occur only for stable conﬁgurations but at

marginal stability (ω = 0) they occur at the resonant surfaces k ·B

= 0. As might

be expected, the instability tends to be localized around the resonant surfaces.

4.7.2 Pressure-driven instabilities

Another interchange instability, discussed by Kruskal and Schwarzschild (1954),

may arise in plasma contained by a magnetic ﬁeld. Here the pressure gradient

plays a role akin to gravity in the Rayleigh–Taylor instability. It is clear from

(4.105) that if the pressure gradient ∇P

and magnetic curvature κ act in the same

direction relative to ξ

⊥

a pressure-driven instability may arise. On the other hand,

if (ξ

⊥

·∇ P

)(ξ

⊥

·κ)<0 this term is stabilizing. Since ∇P

is generally directed

towards the centre of the plasma, the stability condition requires that magnetic cur-

vature be directed outwards (i.e. away from the plasma centre). This conﬁrms our

earlier observation that cusp ﬁelds have favourable curvature whilst those which are

concave towards the plasma have unfavourable curvature. The sausage instability

is an example of an unstable interchange mode resulting from unfavourable cur-

vature. A simple argument similar to that used for the Rayleigh–Taylor instability

allows us to ﬁnd a stability condition for interchange perturbations. We consider a

cross-section of the plasma perpendicular to the ﬁeld lines (again assumed straight)

and perturb it by interchanging two ﬂux tubes of equal strength. This leaves the

total magnetic energy unchanged but, in general, alters the internal energy of the

plasma because both the pressure and the volume may change. The plasma initially

in ﬂux tube 1 with pressure P

and volume V

goes to the position of ﬂux tube 2

with volume V

and, by the adiabatic gas law, pressure P

)

. Thus, the

change in internal energy for ﬂux tube 1 is

)

− P

]/(γ − 1)

4.7 Interchange instabilities 129

Similarly, the change for ﬂux tube 2 is

)

− P

]/(γ − 1)

and letting P

= P

+ δ P, V

= V

+ δV the total change is, to lowest order in

δ P,δV,

δW = γ P

(δV )

+ δ PδV

A sufﬁcient condition for stability is, therefore,

δ PδV > 0 (4.114)

Now if S(l) is the cross-sectional area of a ﬂux tube its volume is



S dl, where dl

is the line element and the integral is taken along the length of the tube. Also, since

the ﬂux is constant along the tube, i.e. B(l)S(l) = , we may write

V = 



B(l)

Thus, if δ P < 0 as we move away from the centre of the plasma we require



B(l)

< 0 (4.115)

which says that the magnetic ﬁeld, averaged along a ﬂux tube, must increase as

we move away from the centre of the plasma. This is the minimum B stability

condition, so called since it requires the plasma to occupy the region where the

average ﬁeld is minimum.

In two- and three-dimensional conﬁgurations there is usually a mixture of

favourable and unfavourable curvature; toroidal conﬁnement devices, for example,

tend to have favourable curvature on the inside of the torus and unfavourable

curvature on the outside. A ﬂux tube may, therefore, experience good and bad

curvature as it winds around the torus. Perturbations will tend to grow in regions

of unfavourable curvature causing the plasma in such regions to balloon out, so

giving rise to the name ballooning instabilities. Since, by deﬁnition one might

say, ballooning instabilities are not controlled by a minimum B (or magnetic well)

conﬁguration they must be avoided by keeping the plasma pressure down, i.e.

stability thresholds for ballooning instabilities set maximum values for β.

Of course, magnetic shear may also be used to stabilize pressure-driven insta-

bilities. The simple argument leading to (4.114) no longer applies when the ﬁeld

is sheared and, as with the Rayleigh–Taylor instability, the instability is localized

near the resonant surfaces. For cylindrical plasmas, where perturbations take the

form (4.75), the resonant surfaces occur at r = r

where

) + kB

) = 0

130 Ideal magnetohydrodynamics

and linear stability analysis involves the minimization of δW around r = r

for

any given m and k. From such an analysis (see Wesson (1981)) one can show that a

cylindrical pinch is stable provided (q



/q)

> −(8µ



/rB

) where q is the safety

factor deﬁned by (4.29). This is Suydam’s criterion which says that the magnetic

shear must be large enough to overcome the destabilizing effect of the pressure

gradient.

4.8 Ideal MHD waves

One of the most interesting aspects of a plasma in a magnetic ﬁeld is the great

variety of waves which it can support. A more complete treatment of waves in

plasmas is deferred to Chapter 6. However, a discussion of ideal MHD at this

point would be incomplete without some account of the natural waves which may

propagate through the plasma. We may expect such waves to be widespread in

space plasmas, where ideal MHD is in general a valid model, and it was in this

context that Alfv

en ﬁrst discovered and described the nature and properties of these

waves.

In order to concentrate on the basic properties we avoid the complications of

boundary conditions by assuming an inﬁnite plasma. Likewise, for simplicity, we

assume that the unperturbed plasma is static and homogeneous. Thus, our starting

point is a plasma with

ρ = ρ

P = P

u = 0 j = 0 B = B

z (4.116)

where ρ

, P

,andB

are constants.

As in our stability investigations we assume a small perturbation of the system

so that in the linear approximation we arrive, as before, at (4.67) but with the

simpliﬁcation that now, in (4.68), ∇ P

= 0 and ∇ × B

= 0. Also, since the

plasma is inﬁnite we may carry out a Fourier analysis in space as well as time, i.e.

we assume ξ(r, t) =

k,ω

ξ(k,ω)e

−i(k·r−ωt)

. Thus (4.67) reads

ξ = kγ P

(k · ξ) +

{[k × (k × (ξ × B

))] × B

} (4.117)

Without loss of generality we can choose Cartesian axes such that k = k

⊥

y+k



and then after expanding the vector products the three components of (4.117) are

(ω

− k



)ξ

= 0 (4.118)

(ω

− k

⊥

− k

)ξ

− k

⊥



= 0 (4.119)

−k

⊥



+ (ω

− k



)ξ

= 0 (4.120)

where c

= (γ P

/ρ

)

1/2

is the sound speed and v

= (B

/µ

)

1/2

is the Alfv

4.8 Ideal MHD waves 131

(a)

(b)

ξ , u, B

B = B

+ B

Fig. 4.31. Shear Alfv

en wave.

speed. The condition for a non-trivial solution (ξ = 0) is that the determinant of

the coefﬁcients should be zero and this gives the dispersion relation



(ω

− k



) 00

0 (ω

− k

⊥

− k

) −k

⊥



0 −k

⊥



(ω

− k



)



= 0

i.e.

(ω

− k



)(ω

− k

+ v

)ω

+ k



) = 0 (4.121)

with solutions

= k



(4.122)

+ v

)[1 ± (1 − δ)

1/2

] (4.123)

where

δ = 4



+ v

)

(4.124)

Since 0 ≤ δ ≤ 1, all three solutions are real and the waves propagate without

growth or decay. There is neither dissipation to cause decay nor free energy (cur-

rents) to drive instabilities.

Taking each mode in turn, (4.122) is the dispersion relation for the shear Alfv

wave. As is clear from (4.118)–(4.120), this mode is decoupled from the other two

and its displacement vector ξ

x is perpendicular to both B

and k, i.e. the wave,

illustrated in Fig. 4.31(a), is transverse. Note that, from (4.62) and (4.64), B

and

u = u

are in the same direction as ξ. Since k · ξ = 0, we see that ρ

and P

are

both zero, i.e. the wave is incompressible. It propagates, as shown in Fig. 4.31(b),

132 Ideal magnetohydrodynamics

like waves along plucked strings under tension, the strings being the magnetic ﬁeld

lines. In fact Alfv

en, using the analogy with elastic strings, pointed out that the

phase velocity obtained is exactly what one would expect if one substitutes the

magnetic tension B

/µ

for T in the expression ω/k = (T /ρ

)

1/2

for the phase

velocity of transverse waves along strings with line density ρ

and tension T . The

energy in the wave oscillates between plasma kinetic energy

and perturbed

magnetic energy B

/2µ

. This conﬁrms the statement about the ﬁrst term in the

integrand of δW

in (4.105).

The two remaining modes have ξ

= 0 = u

. Observing that the minimum

(maximum) value of ω

, when we take the plus (minus) sign in (4.123), is given

by δ = 1, it follows that ω

≥ k



≥ ω

, where ω

F,S

are the fast and slow wave

frequencies corresponding to the plus and minus signs, respectively. Since both

the magnetic (Alfv

en) and acoustic wave speeds appear in the dispersion relation

for these waves and they are compressional they are known as the fast and slow

magnetoacoustic waves. To discuss these modes we note, from (4.119) and (4.120),

that they decouple when propagation is either parallel or perpendicular to B

For perpendicular propagation (k



= 0) the fast wave has

= k

+ v

)

and the displacement vector ξ = ξ

y is parallel to k = k

⊥

y. From (4.62), B

parallel to B

so the compression of the magnetic ﬁeld combines with that of the

plasma (P

∝ k · ξ) to drive the wave. The slow wave does not propagate in this

direction (ω = 0).

In the case of parallel propagation (k

⊥

= 0), one mode has ω = kv

and ξ

= 0

and the other, ω = kc

and ξ

= 0. In this limit the magnetoacoustic waves have

separated into a compressional Alfv

en wave and an acoustic wave. Which mode is

fast and which slow depends on the relative magnitudes of v

and c

but usually

β<1 in which case the acoustic wave is the slow mode. In the acoustic wave the

displacement vector is along B

so the ﬁeld plays no role; the wave is driven by the

ﬂuctuations in gas pressure. On the other hand, in the compressional Alfv

en wave

k · ξ ∼ k · u ∼ ∇ · u = 0 so that the compressibility of the plasma has no effect.

For propagation at arbitrary angles to the magnetic ﬁeld, these modes are cou-

pled. In the low β limit c

 v

so that ω

≈ kv

and ω

≈ k



. Thus, for the

fast mode, from (4.120) we see that |ξ

|/|ξ

|∼β  1, i.e. the plasma motion is

almost perpendicular to the ﬁeld lines. The oscillation in energy is between plasma

kinetic energy and ﬁeld energy (compression and tension). Likewise, for the slow

mode in the low β limit, from (4.119) we see that |ξ

|/|ξ

|∼β  1 so the plasma

motion is almost parallel to B

. Here energy oscillates within the plasma between

kinetic and internal energy.

Exercises 133

Exercises

4.1 Consider the steady ﬂow u = u(z)

x of a viscous conducting ﬂuid between

inﬁnite horizontal planes at z = 0 and z = 2d driven by the motion of the

upper plane with velocity V

x relative to the ﬁxed plane at z = 0. Given

that the ﬂow, known as Couette ﬂow, is subject to a constant applied mag-

netic ﬁeld B

z but that there is no electric ﬁeld (short-circuit condition),

verify that the solution of the equation set

= j ×B −∇P + µ



∇

u +

∇(∇ · u)



j = σ(u ×B)

= ∇ × B/µ

is u(z) = V

sinh(Hz/d)/ sinh 2H where H = B

d(σ/µ)

1/2

is the Hart-

mann number. (Assume that all variables depend only on z).

Consider the limits H → 0 and H →∞to show that as B

→ 0

the hydrodynamic ﬂow u(z) = V

z/2d is recovered, whilst as µ → 0

the inviscid solution (u(z) ≡ 0) is not retrieved but the ﬂow is effectively

restricted to a boundary layer at the moving plane, the thickness of which

tends to zero as H

−1

4.2 Derive the equation of energy conservation (4.3) from the ideal MHD

equations in Table 3.2.

4.3 Show that the Bennett electron density proﬁle n

(r) = n

(0)[1+(r/r

)

]

−2

in a Z -pinch corresponds to uniform electron ﬂow velocity across the

plasma column. Evaluate the scale length r

Using (4.23)–(4.28) show that the pressure, magnetic ﬁeld and current

proﬁles are given by

P(r) =

8π

)

B(r) =

2π

j (r) =

)

(E4.1)

Sketch these proﬁles and show that for r > r

both the plasma and mag-

netic pressure gradients are negative. It is the magnetic tension −B

/µ

acting against this combined outward pressure, which constrains the

plasma in the equilibrium conﬁguration.

134 Ideal magnetohydrodynamics

4.4 Solov’ev (1968) found an exact axisymmetric solution to the Grad–

Shafranov equation (4.44) with

P =−|P



|ψ + P

= 2γ(1 +α

)

−1



|ψ + F

where P

and (F

) denote the pressure and magnetic ﬁeld on the mag-

netic axis R = R

, Z = 0, ψ = 0. Check that with this choice a solution

to the Grad–Shafranov equation (setting µ

= 1) is

ψ =



2(1 + α

)



− γ)Z

− R

)



Setting R − R

= x  R

show that the magnetic surfaces have

approximately elliptical cross-sections

[x + δ(x, Z )]



− γ



= x

Determine the Shafranov shift δ(x, Z ) which has the effect of shifting

the magnetic axis, compressing the magnetic surfaces on the outside and

relaxing their separation on the inside (see Fig. 4.19(c)).

4.5 Starting from the expression



/2µ

)dτ

for the magnetic energy in a volume V , show that δW = 0 leads to



dτ B · (∇δα × ∇β + ∇α × ∇δβ ) = 0

if B = ∇α × ∇β, where the Clebsch variables α and β are constant on

the bounding surface.

Integrate this equation by parts to obtain



dτ {[∇β · (∇ × B)]δα − [∇α · (∇ × B)]δβ }=0

and hence deduce the coupled differential equations (4.51) for α and β.

4.6 A simple model represents a sunspot as a ﬂux cylinder in which B =

B(r)

z, g =−g

z and with radially decreasing magnetic pressure and in-

creasing plasma pressure. Starting from the magnetohydrostatic condition

(4.52) and assuming that the ﬁeld vanishes at the edge of the sunspot, show

that the pressure balance condition is

int

(r, z) +

(r)

2µ

= P

ext

(z)

Exercises 135

where P

int

and P

ext

are the internal and external plasma pressures, respec-

tively. Show also that the density

ρ =−

ext

is a function of z only. Hence, deduce the temperature ratio

int

(r, z)

ext

(z)

int

(r, z)

ext

(z)

= 1 −

(r)

2µ

ext

(z)

showing that a vertical magnetic ﬁeld may produce a temperature deﬁcit

inside the sunspot.

4.7 By taking the scalar product of (4.67) with ξ

∗

and subtracting its complex

conjugate show that

[ω

− (ω

∗

)

]



|ξ|

dr =



[ξ

∗

· F(ξ) − ξ · F(ξ

∗

)]dr

Deduce that the self-adjointness of F(ξ) implies that the eigenvalues ω

are real.

From the equation

= δW (ξ

∗

, ξ)/K (ξ

∗

, ξ)

where δW (ξ

∗

, ξ) =−



∗

· F(ξ)dr and K (ξ

∗

, ξ) =



|ξ|

dr, show

that the varation ξ → ξ +δξ,ω

→ ω

+δω

, for small δξ and δω

, leads

δω

= δW (δξ

∗

, ξ) +δW (ξ

∗

,δξ) −ω

[K (δξ

∗

, ξ) + K (ξ

∗

,δξ)]/K (ξ

∗

, ξ)

Hence, using the self-adjoint property of F and setting δω

= 0, corre-

sponding to ω

being an extremum, show that



dr{δξ

∗

· [F(ξ) + ω

ξ] + δξ · [F(ξ

∗

) + ω

∗

]}=0

and from this deduce the equivalence of the variational principle discussed

in Section 4.6 and the normal mode eigenvalue equation (4.67).

4.8 By following the steps indicated in the text derive (4.101) from (4.96).

Show further, by separating vector quantities into parallel and perpen-

dicular components, X = X



b + X

⊥

, where b is a unit vector in the

direction of the magnetic ﬁeld, that the expression (4.102) for δW

may

be written in the form (4.105).

4.9 Show that the same procedure used to derive (4.112) leads to the dispersion

relation (4.113) for the case of an unmagnetized plasma of constant density

supported by a constant magnetic ﬁeld B

136 Ideal magnetohydrodynamics

4.10 Consider a plasma with a perturbed rippled boundary (see Fig. 4.29(a))

containing a uniform magnetic ﬁeld B

= B

z in a gravitational ﬁeld.

According to Section 2.3.1 a positive ion is then subject to a gravitational

drift along −

x. Sketch the effect of this drift on the charge on adjacent

sides of the ripple, including the direction of the induced electric ﬁeld δE.

Show that the resultant δE × B

drift acts in such a way as to amplify the

original rippled perturbation.

4.11 Magnetic buoyancy can lead to instability. By considering an isolated ﬂux

tube rising adiabatically along the z-axis in a conducting ﬂuid containing

a magnetic ﬁeld B = B

(z)

x, show that this rise becomes unstable if the

ﬁeld decays with z faster than the density ρ, i.e. if d(B

/ρ)/dz < 0.

The magnetic buoyancy instability is a special case of the Rayleigh–

Taylor instability. How is the instability condition modiﬁed when curvature

of the ﬁeld lines is taken into account (see Parker (1979))?

4.12 Show that if the radius of curvature R

(see Section 2.4.2.) and g are in the

same direction, the drift v

, given by (2.24), is equivalent to a gravitational

drift with g = (v

⊥

+ 2v



)/2R

By averaging over a velocity distribution for a thermal plasma show that

this orbit theory result leads to the condition g = 2P/ρ R

where P and ρ

denote the ion pressure and density respectively.

By analogy with the result from Exercise 4.10, a plasma in a curved

magnetic ﬁeld should show a similar tendency for charge to build up and

hence become unstable. Deduce that instability occurs when the plasma

is conﬁned by a magnetic ﬁeld that is concave towards the plasma. By

analogy with the Rayleigh–Taylor growth rate show that the growth rate of

this ﬂute instability is γ = (2∇P/ρ R

)

1/2

4.13 Show that Suydam’s criterion in Section 4.7.2. can be expressed in the

form s

>(8r

)κ

∇P, where s = dlnq/dlnr is the shear parame-

ter and κ

=−B

r/B

r is the ﬁeld line curvature vector in cylindrical

geometry.

For toroidal geometry substitute κ = κ

+ κ

where κ

=−

R/R is the

curvature of the toroidal magnetic ﬁeld. Show that although κ

∼ κ

(R/r),

is along ∇P on the outside of the torus but in the opposite direction on

the inside and hence, following a ﬁeld line, destabilizing and stabilizing

contributions alternate so that the effect of toroidal curvature averages out

to lowest order.

Show that by going to next order and averaging over a ﬁeld line, assum-

ing concentric circular ﬂux surfaces, one ﬁnds an approximate toroidal

curvature of (1 − q

/2)κ

. A rigorous calculation gives in fact (1 − q

)κ