Boyd T.J.M., Sanderson J.J. The Physics of Plasmas

Подождите немного. Документ загружается.

5.3 Resistive instabilities 157

∇

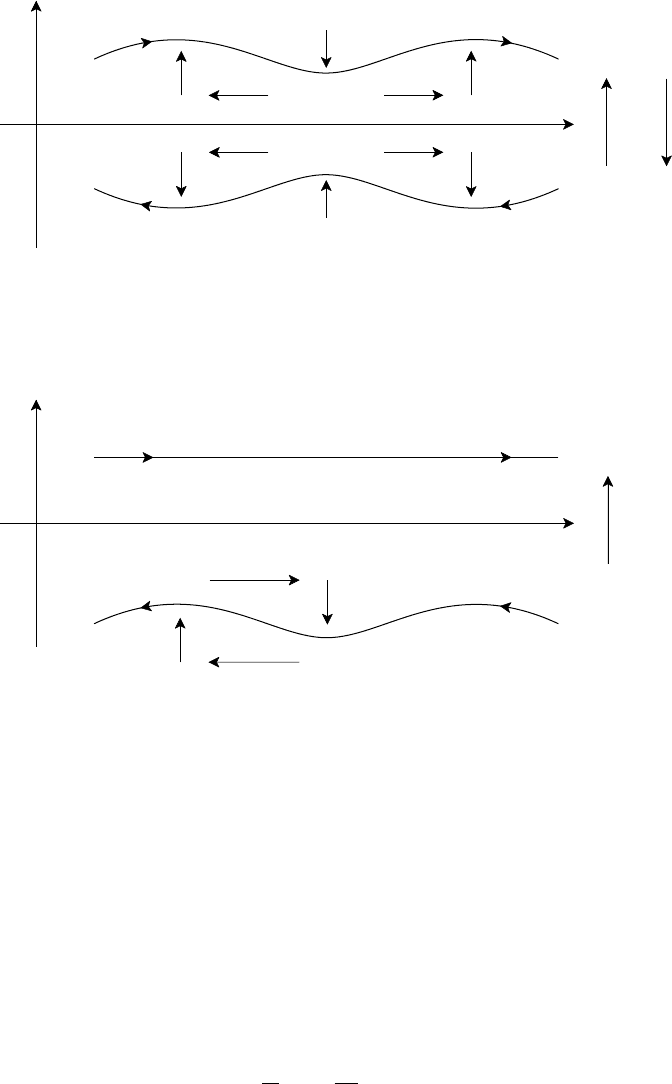
(b) Rippling mode

∇

(a) Resistive g mode

Fig. 5.8. Plasma motion relative to ﬁeld lines in (a) gravitational interchange mode and (b)

rippling mode.

5.3.3 Tokamak instabilities

Although we have considered only the simplest geometry of a slab plasma, the

tearing mode makes its appearance in cylindrical and toroidal plasmas in which

the resonant surfaces occur at the mode rational surfaces. In toroidal geometry in

which perturbations vary as A(r)e

i(mθ−nφ)

, θ and φ being the poloidal and toroidal

angles and r the minor radius, the condition k ·B

= 0 becomes

−

= 0

158 Resistive magnetohydrodynamics

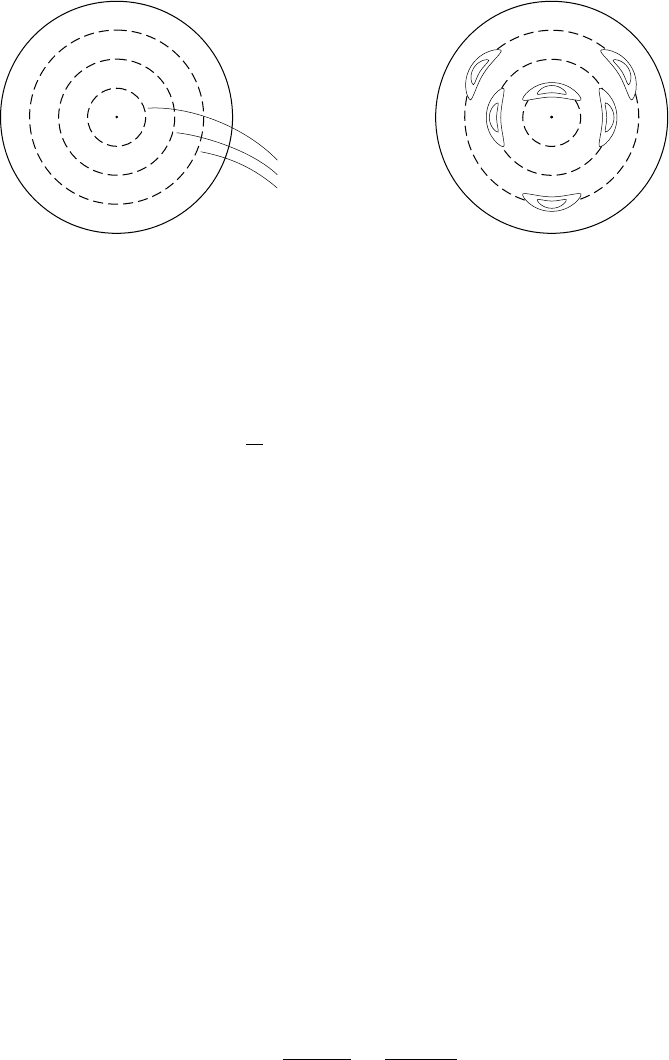
(a) (b)

mode

rational

surfaces

m = 1

m = 2

m = 3

Fig. 5.9. Formation of magnetic islands at resonant surfaces in a tokamak.

For a circular torus of large aspect ratio we may substitute (4.35) to write this as



− q(r)



(r) = 0

showing that resonant surfaces occur at r = r

where

q(r

) = m/n

These are the mode rational surfaces. Figure 5.9 shows the formation of magnetic

islands at the resonant surfaces corresponding to m = 1, 2 and 3. The mode rational

surfaces on which these islands appear are shown in Fig. 5.9(a). With magnetic

shear, q(r) increases with r and the magnetic ﬁeld lines on any surface r = r

close on themselves after n circuits around the torus. (For all other values of r the

ﬁeld lines continue to wind around the torus without ever closing and eventually

cover all of the surface. Such ﬁeld lines and surfaces are said to be ergodic, as

mentioned in the discussion of the rotational transform in Section 4.3.2.) The

magnetic islands that form at the mode rational surfaces also twist around the torus

closing on themselves after n times. Since heat ﬂows rapidly along ﬁeld lines one

of the consequences of this structure is an increase in transport across the plasma.

Tearing mode instabilities are believed to be the source of Mirnov oscillations

which are magnetic ﬂuctuations, ﬁrst detected by Mirnov and Semenov (1971),

occurring during the current rise in tokamaks. The azimuthal variation of the ﬂuc-

tuations shows them to be associated with a succession of decreasing m numbers

as the current rises and the q value at the plasma surface decreases according to

q(a) =

(a)

2πa

5.3 Resistive instabilities 159

(kA)

magnetic

signal

100

t(ms)

m = 6 m = 5

m = 4

Fig. 5.10. Mirnov oscillations (after Mirnov and Semenov (1971)).

where from (4.73) we have substituted µ

I = 2πaB

(a). Time variations are

illustrated in Fig. 5.10. Note that these oscillations persist beyond the current rise.

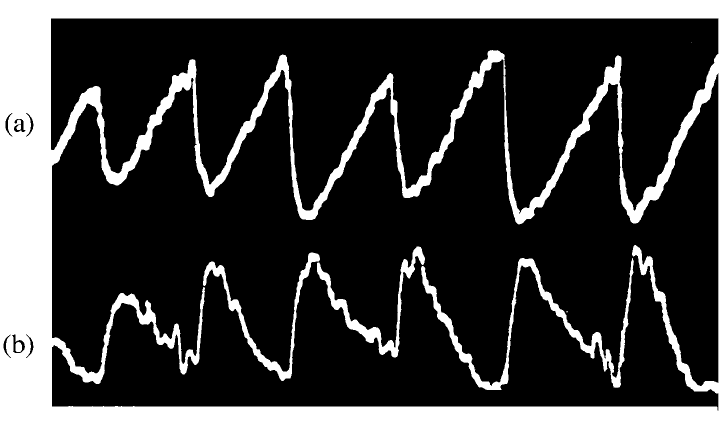
Sawtooth oscillations, observed in the soft X-ray emission from tokamaks, are

evidence of another instability, in this case thought to be the m = 1 kink mode

occurring in the centre of the plasma. The name arises from the shape of the oscil-

lations which show a slow rise over a period of about 1 ms followed by a sudden

fall; X-rays from the outer region of the plasma show the inverse pattern of a slow

decay followed by a rapid rise, indicating that temperature changes in the outer

plasma compensate those occurring in the central plasma due to the instability.

These are illustrated in Fig. 5.11.

The slow build-up in the inner region arises because the plasma is hotter there

and, since conductivity increases with temperature, any increase in axial current

160 Resistive magnetohydrodynamics

Fig. 5.11. Sawtooth oscillations in X-ray emission from (a) the central region and (b) the

outer region of a tokamak plasma (after Wesson (1987)).

means increased ohmic heating leading to an unstable concentration of current in

the centre of the plasma. Now as the axial current increases so does the poloidal

magnetic ﬁeld and for sufﬁciently large current the safety factor q may fall below

unity allowing a q = 1 surface to appear near the axis. This is illustrated in Fig.

5.12 which shows the subsequent development of the m = 1 instability at the q = 1

surface. The shaded region is the hot q < 1 island. The growth of the q > 1 island

displaces it to the outer region where it slowly decays and disappears by thermal

conduction to the cooler plasma. The equilibrium ﬁeld structure is restored and

the procedure is repeated. The rapid reconnection phase, (iii)–(v), produces the

sudden fall (rise) in temperature in the inner (outer) region of the plasma and the

corresponding patterns in soft X-ray emission.

Neither Mirnov nor sawtooth instabilities prevent the satisfactory operation of

tokamaks. On the other hand, a third resistive instability leads to the collapse

of the plasma current and it is therefore known as the disruptive instability. The

principal characteristics of the disruptive instability are a rapid broadening of the

current proﬁle with consequent decrease in the poloidal ﬁeld, followed by a loss of

thermal energy from the plasma to a degree that quenches the discharge. In general

the instability is interpreted in terms of a model in which magnetic surfaces are

destroyed by tearing modes with different helicities at different resonant surfaces.

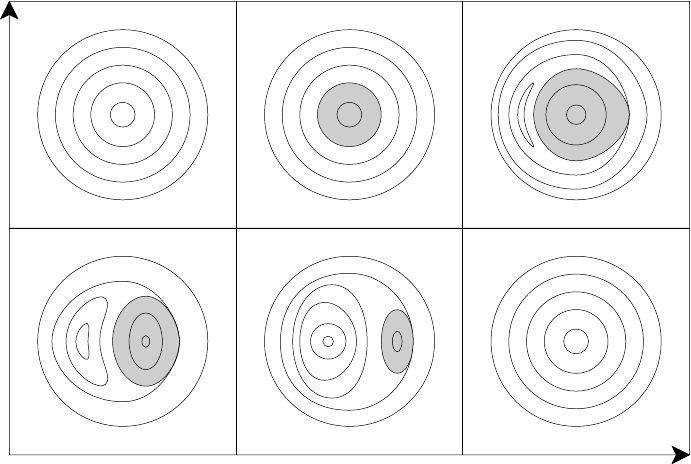
5.3 Resistive instabilities 161

(ii)(i) (iii)

(iv) (v)

(vi)

Fig. 5.12. Development of m = 1 instability at q = 1 surface (after Wesson (1987)).

Plasma containment breaks down with loss of energy from the tokamak by means

of heat transport along the ﬁeld.

The disruptive instability is the least well understood of the tokamak instabilities

but observations indicate that the m = 2 tearing mode is crucially involved. In the

earliest phase the m = 2 instability is saturated at a low level but slowly increasing

density or current triggers the precursor phase in which the unstable oscillations

reach much higher amplitudes. Since other low m modes are observed in this phase

it is possible that a non-linear interaction of the m = 2 mode with the m = 1

sawtooth or m = 3(n = 1 or 2) modes is involved, though other interactions with

the outer region of the plasma or the limiter are possible. Whatever the mechanism,

the growth in amplitude over a period of about 10 ms triggers the fast phase in

which the central temperature collapses and the radial current proﬁle ﬂattens in

a time of the order of 1 ms. This is followed by the quench phase in which the

plasma current decays to zero. Fuller discussions of the disruptive instability are

to be found in Wesson (1987) and Biskamp (1993). The phases of a disruptive

instability driven by increasing density are illustrated schematically in Fig. 5.13

which sketches the time development of the m = 2 magnetic ﬁeld ﬂuctuations,

central temperature, and plasma current.

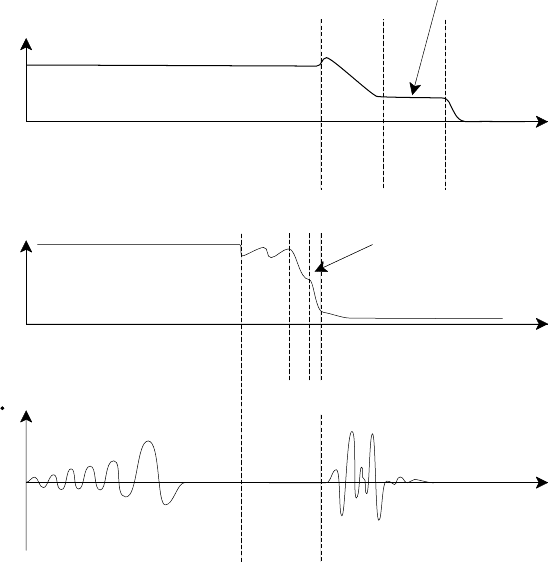
162 Resistive magnetohydrodynamics

precursor phase

runaway current

major disruption

Fig. 5.13. Disruptive instability.

5.4 Magnetic ﬁeld generation

Magnetic ﬁelds pervade the Universe ranging in magnitude from background levels

of about 10

−10

T to as high as 10

T in neutron stars. Understanding why large scale

magnetic ﬁelds occur in stars and galaxies remains a key concern in astrophysics

(Field (1995)). A detailed discussion of the problems of ﬁeld generation has been

given by Parker (1979). Here we limit our discussion to a brief outline of some

basic ideas. The contraction of gas leading to formation of galaxies carried with it

some part of the primordial magnetic ﬁeld so that each galaxy, when formed, had

within it a magnetic ﬁeld. In the same way diffuse interstellar gas clouds condens-

ing to form stars had remnants of the primordial ﬁeld trapped within. However, in

due course magnetic buoyancy and diffusion might be expected to disperse such

ﬁelds except possibly for some fragment preserved within the (stable) inner core

of stars. Consequently, one of the most long-standing and challenging problems in

MHD has been to explain just how the observed magnetic ﬁelds of stars and planets

are sustained.

5.4 Magnetic ﬁeld generation 163

There are two possible mechanisms by which magnetic ﬁelds may be regener-

ated, by means of a dynamo or a battery. A dynamo mechanism necessarily requires

some initial ﬁeld on which the ﬂuid motion can act. This is not a requirement for

the battery mechanism suggested by Biermann (1950) which in the event proved

to be incapable of generating sufﬁciently strong ﬁelds. However, as Parker (1979)

remarks, the real signiﬁcance of the Biermann battery is that it guarantees, if all

else fails, a seed ﬁeld for stars and galaxies. We turn now to an outline of some

aspects of dynamo action.

5.4.1 The kinematic dynamo

One obvious source of energy for the regeneration of magnetic ﬁelds is the kinetic

energy in ﬂow ﬁelds. Dynamo action amounts to the systematic conversion of the

kinetic energy of the ﬂow ﬁeld into magnetic ﬁeld energy. The full dynamo problem

is formidable since the regeneration of the ﬁeld must come via the convection term

in (5.1) and so what is required is the simultaneous solution of this equation for B

and the equation of motion for u. The difﬁculties of this task are such that work

has mostly been concentrated on the kinematic dynamo problem in which one tries

to devise a ﬂow ﬁeld which will maintain a magnetic ﬁeld against resistive decay,

i.e. (5.1) is to be solved for B when u(r, t) is given.

Paradoxically, a major advance in kinematic dynamo theory was made in 1934

by Cowling’s proof of an anti-dynamo theorem (Cowling, 1976). Using a simple

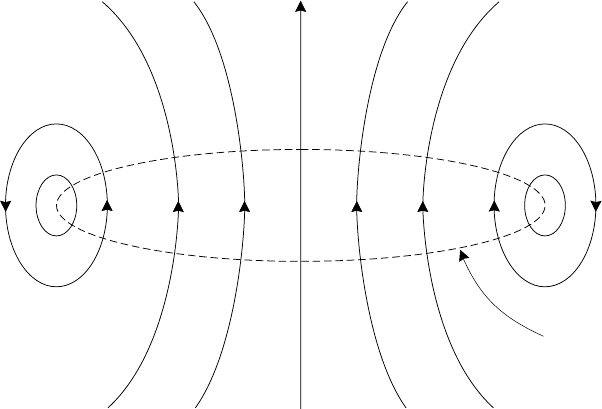
argument he showed that a steady, axisymmetric magnetic ﬁeld cannot be main-

tained. In the case that he considered both the ﬂow and the ﬁeld lines are in a

meridional plane through the axis of symmetry. In any such plane the ﬁeld lines

must be closed curves enclosing at least one neutral line as shown in Fig. 5.14.

Then if we integrate Ohm’s law around this line we get



j · dl = σ



E · dl + σ



u × B · dl

= σ



∇ × E · dS =−σ



∂B

∂t

· dS = 0 (5.25)

where the integral of the convection term vanishes on account of the fact that B is

zero along the neutral line and the ﬁnal integral vanishes because, by assumption,

∂B/∂t = 0. But (5.25) implies that j

= 0 which is clearly incompatible with

Amp

ere’s law, µ

j = ∇ ×B, and the contradiction proves the theorem. The physi-

cal interpretation of the theorem is that while the convection term can transport the

ﬁeld lines in the meridional plane it cannot create new ﬁeld lines to replace those

that diffuse through the plasma and disappear at the neutral point.

The proof of Cowling’s theorem can be extended to include an azimuthal com-

ponent of the magnetic ﬁeld. In this case u × B · dl = 0 on the neutral line since

164 Resistive magnetohydrodynamics

neutral line

Fig. 5.14. Geometry of ﬁeld lines in Cowling’s theorem.

B and dl are parallel. Further generalizations of the anti-dynamo theorem exist

for ﬁeld conﬁgurations which are topologically similar to the axisymmetric case.

The conclusion is that although a spherical body like a star or planet may have a

dominant axially symmetric dipole ﬁeld at its surface, the magnetic ﬁeld within the

body must be considerably more complicated if it is to be maintained by dynamo

action.

Cowling’s theorem and extensions of it are important in ruling out ﬁelds and

ﬂuid motions with certain simple structures. The question remains as to what

properties are required of the motion for magnetic ﬁelds to be generated? In the

most general terms the answer appears to be that differential (non-uniform) rotation

and turbulent convection are required.

Following Cowling’s theorem it took more than twenty years before Herzen-

berg (1958) and Backus (1958) proved existence theorems for possible dynamo

mechanisms for steady and oscillating ﬁelds, respectively. This led to the develop-

ment of other dynamo models and the emphasis of research was able to turn from

mere existence to possible relevance. Subsequently, progress has been more rapid

so that the kinematic problem is now broadly understood and, despite its mathemat-

ical complexity, considerable advances have been made towards the ultimate goal

of a self-consistent solution of the dynamic problem. The brief qualitative account

of the essential physics of the dynamo action presented here follows closely the

decriptions given by Moffat (1993) and Field (1995).

5.4 Magnetic ﬁeld generation 165

stretch

twist

fold

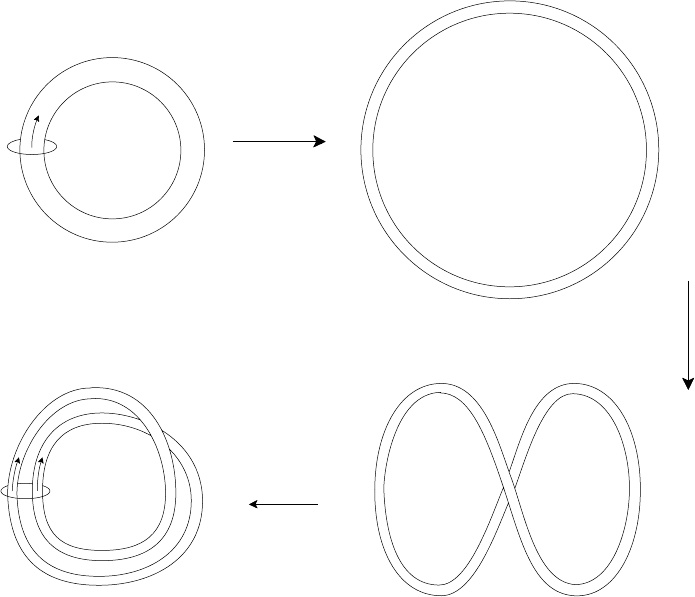
Fig. 5.15. Increase in ﬁeld strength by stretch, twist and fold sequence (after Moffat

(1993)).

We have seen already in Section 4.2 how a ﬂow which stretches a magnetic

ﬂux tube increases the ﬁeld strength. Continuing the analogy, we may suppose that

the ﬂux tube is stretched to twice its original length and then twisted and folded,

as illustrated in Fig. 5.15, to obtain a ﬁeld of twice the original strength through

the ﬁxed loop C. Of course, such a stretch–twist–fold cycle, suggested originally

by Zel’dovich in 1972, merely illustrates how the ﬁeld strength may be increased

from an arbitrarily low level and it is necessary to explain what kind of a ﬂow might

realistically produce this effect. The answer lies in the combination of two physical

processes known as the α- and -effects.

It is assumed that u and B consist of slowly varying axisymmetric mean compo-

nents and weak small scale ﬂuctuating components:

u =u+u



B =B+B



166 Resistive magnetohydrodynamics

Averaging the induction equation over the small scale ﬂuctuations gives

∂B

∂t

= ∇ × [u×B] +∇ ×u



× B



+η∇

B (5.26)

Subtracting this equation from (5.1) then gives the evolution equation for B



namely,

∂B



∂t

= ∇ × [u×B



+ u



×B] + ∇ × [u



× B



−u



× B



] + η∇



(5.27)

Since we may transform to a coordinate system in which u=0 the basic

task of kinematic dynamo theory is to solve (5.27) for B



in terms of u



and B

and substitute in the second term on the right-hand side of (5.26). This is the

crucial ‘extra’ term (compared with the induction equation containing only the

mean axisymmetric ﬂow and ﬁeld) which permits dynamo action to take place. It

does so by means of a regenerative cycle in which a toroidal ﬁeld B

is created from

a poloidal ﬁeld B

by means of the -effect while the combination of diffusion and

the α-effect acts on B

to regenerate B

. The -effect arises from the ﬁrst term on

the right-hand side of (5.26) and is relatively simple to understand as explained

below. The α-effect comes from the second term ∇ ×u



× B



 and is much more

subtle. Speciﬁcally, under certain simplifying assumptions one can show that

u



× B



=−αB+β∇ ×B

where α =u



· ∇ × u



τ/3, β =u



· u



τ/3andτ is the velocity correlation

time. The β term enhances the diffusion whilst the α term, provided the helicity is

non-zero, regenerates the mean poloidal ﬁeld.

The -effect takes its name from the symbol used to denote the rate of angular

rotation of a conducting sphere, which is assumed to vary with distance from the

axis of rotation. Such a differential rotation rate arises when convection currents

are subject to a combination of buoyancy and Coriolis forces. The essential point

is that, by conservation of angular momentum, descending ﬂuid elements increase

their rate of rotation. Consequently, a ﬁeld line passing through the rotating sphere

is wound around the axis of rotation rather than simply being carried around, as

would be the case if the rotation rate was uniform. As Fig. 5.16 shows, this creates

a toroidal ﬁeld component B

from what was originally a purely poloidal ﬁeld B

;

note, also, that B

is antisymmetric about the equatorial plane.

The α-effect does the opposite, creating a poloidal component B

from a purely

toroidal ﬁeld B

. Consider the ﬂow ﬁeld

u = (0, u

cos(kx − ωt), u

sin(kx − ωt))

which represents a circularly polarized wave travelling along the x-axis as shown

in Fig. 5.17(a). It is easily veriﬁed that the vorticity ω ≡ ∇ ×u =−ku and hence