Boyd T.J.M., Sanderson J.J. The Physics of Plasmas

Подождите немного. Документ загружается.

Exercises 137

Using this result write down the toroidal analogue of Suydam’s criterion

(see Biskamp (1993)).

4.14 In practice since most problems in MHD have to be solved numerically it

is often preferable to integrate the MHD equations numerically from the

start. A simple introduction to computational MHD is provided by a one-

dimensional Lagrangian code. In a Lagrangian ﬁnite difference scheme the

grid points of the ﬁnite difference scheme move with the ﬂuid. This has the

advantage that the advective term in the MHD equations is replaced by the

Lagrangian time derivative which means that the complication inherent in

these terms is transferred to the equation of motion for the mesh dx/dt =

v. In other words in a Lagrangian scheme one labels a differential mass of

ﬂuid by its position at t = 0, say x

(t = 0) and then determines x as well

as the velocity, pressure, density etc. of this same differential mass of ﬂuid

as time evolves.

Deﬁning a space mesh with mesh points j moving with the ﬂuid veloc-

ity, i.e. x

n+1

= x

+ v

t and the cell width by 

n+1

= x

n+1

j+1

− x

n+1

the MHD equations integrated on this mesh have the form:

(X ) = 0

(Pρ

−γ

) = 0

=−

∂

∂x



P +

2µ



where X = (ρ, B).

The ﬂuid properties are expressed as cell quantities deﬁned at the centre

of each cell, i.e.

n+1

= X



j+1

− x





n+1

j+1

− x

n+1



n+1





n+1





The pressure is then used to recalculate the velocity of the boundary for

each cell:

= v

n−

−

2t



+ ρ

j−





∗n

− P

∗n

j−





− x

j−



where P

∗

= P + B

/2µ

. Not only is a one-dimensional Lagrangian

mesh simple conceptually, but the mesh itself reﬂects ﬂuid behaviour

through successive bunching and spreading of cell boundaries giving rise

to sound waves on the mesh. As wave proﬁles steepen to form shocks the

Lagrangian mesh automatically accumulates mesh points in the region of

the shock front which is beneﬁcial for spatial resolution.

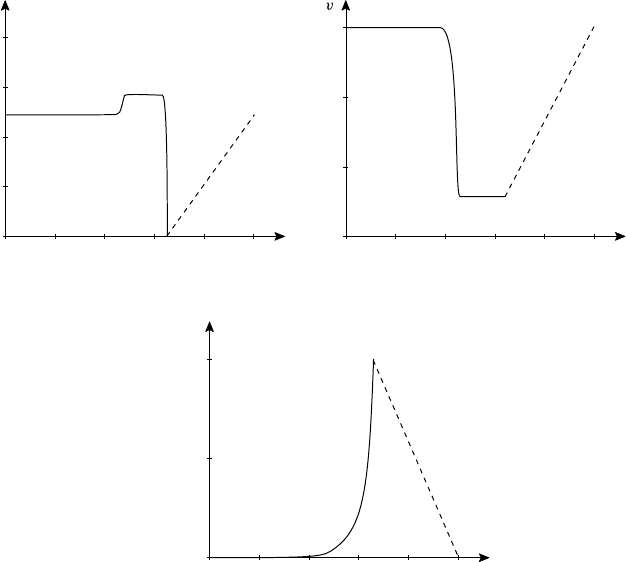
138 Ideal magnetohydrodynamics

0.01

0.1

-1

-2

Fig. 4.32. Time-frame from a 1D Lagrangian code output showing density ρ,

velocity v, and magnetic ﬁeld B proﬁles as functions of radius, representing a

shock imploding on a plasma slab from the right (arbitrary units).

The project involves using the Lagrangian scheme outlined to model

shock implosion leading to the formation of a pinch. A shock is applied at

the right-hand boundary of a plasma slab and propagates inwards. Choose

suitable initial values for plasma parameters and integrate the equations

of motion to determine ρ, v and B as the shock propagates inwards. The

proﬁles in Fig. 4.32 are typical.

However, your output is likely to show small scale oscillations at the

shock front which are computational rather than physical. Representing a

shock on a difference mesh presents problems since by deﬁnition a shock

front is steep and short wavelengths cannot be represented on the mesh.

We shall ﬁnd in Chapter 5 that shock thickness is determined by viscosity.

Within the framework of ideal MHD we have to resort to introducing an

artiﬁcial viscosity which has the effect of suppressing discontinuities with

a wavelength less than the step size of the space mesh, while leaving longer

Exercises 139

wavelengths unaffected. This artiﬁce serves to remove oscillations that

otherwise appear in the region of shock compression. To make this change

we replace P





where r denotes the numerical

viscosity. The particular representation adopted for the artiﬁcial viscosity

is not critical. Numerical viscosity was included in the scheme used to

produce the snapshots of the implosion in Fig. 4.32.

Resistive magnetohydrodynamics

5.1 Introduction

Although ideal MHD is often a good model for astrophysical and space plasmas

and is widely employed in fusion research it is never universally valid, for the

reasons discussed in Section 4.1. In this chapter we consider some of the most

important effects which arise when allowance is made for ﬁnite resistivity and, in

the case of shock waves, other dissipative mechanisms. Even though the dissipation

may be very weak the changes it introduces are fundamental. For example, ﬁnite

resistivity enables the plasma to move across ﬁeld lines, a motion forbidden in ideal

MHD. Usually, the effects of this diffusion are concentrated in a boundary layer so

that mathematically the problem is one of matching solutions, of the non-ideal

equations in the boundary layer and ideal MHD elsewhere. On the length scale of

the plasma the boundary layer may be treated as a discontinuity in plasma and ﬁeld

variables and, depending on the strength of the ﬂow velocity, this discontinuity

may appear as a shock wave.

A comparison of Tables 3.1 and 3.2 reveals that the difference between resistive

and ideal MHD is the appearance of extra terms proportional to the plasma resis-

tivity, η ≡ σ

−1

, in the evolution equations for P and B. Although one is tempted,

therefore, to think of ideal MHD as the zero resistivity limit we know from the

discussion in Section 3.3.2 that it is properly regarded as the inﬁnite magnetic

Reynolds number or large length scale limit, an observation that arises from a

comparison of the diffusion and convection† terms in the induction equation

∂B

∂t

∇

B + ∇ × (u × B) (5.1)

The characteristic times for resistive diffusion and convection are, respectively,

∼ µ

/η and the Alfv

en transit time τ

∼ L/v

, where, anticipating that

we shall be interested mainly in ﬂows dominated by the magnetic ﬁeld, we have

† The convection term is known also as the advection term.

140

5.1 Introduction 141

Table 5.1. Characteristic lengths, times and Lundquist numbers

(m)τ

(s)τ

(s) S

Arc discharge 10

−1

−3

Tokamak 1 1 10

−8

Earth’s core 10

Sunspot 10

Solar corona 10

approximated |u| by the Alfv

en speed v

and L is an appropriate length scale. With

this choice and L = L

, the hydrodynamic length scale, the magnetic Reynolds

number is usually denoted by S = τ

/τ

and referred to as the Lundquist number.

For high temperature laboratory plasmas S is typically 10

–10

and several orders

of magnitude greater still for astrophysical plasmas. Table 5.1 shows characteristic

values for various plasmas.

Some of these time scales at ﬁrst sight look rather surprising. For example, they

indicate that the diffusion time for a sunspot is millions of years when we know

that sunspots seldom last longer than a few months. By contrast, they suggest that

the Earth’s magnetic ﬁeld should have diffused away relatively early in its lifetime.

The fallacy comes from equating diffusion time with lifetime. The Earth’s ﬁeld

persists because some regenerative process is at work compensating for diffusive

decay and sunspots disappear on a time scale governed, not by the slow diffusion

of their ﬁelds through the photosphere, but by some much faster mechanism. How

do these other physical processes come into effect when the very large values of

S in Table 5.1 suggest that ideal MHD is a more than adequate approximation for

fusion and space plasmas?

The answer to this question is twofold. First, we note that S = µ

L/η and

we have used L = L

in Table 5.1. Then we must remember that the dimensional

comparison of diffusion and convection terms is a crude argument. If, somewhere

in the plasma, the convection term vanishes there will be a local region in which

the diffusion term, however small, will come into play. Thus, the signiﬁcance of

large S is not that resistivity is entirely negligible but rather that, compared with

, the length scale of the region in which it need be considered is very small.

In other words, although ideal MHD may be valid for most of the plasma, there

can be narrow boundary layers such as current sheets, in which we must apply

resistive MHD. We shall see that within such regions plasma relaxation involves the

reconnection of magnetic ﬁeld lines, generally reducing a complex ﬁeld topology

to one with simpler connectivity, thereby enabling the system to arrive at a lower

energy state. These topological changes in the magnetic ﬁeld take place on a time

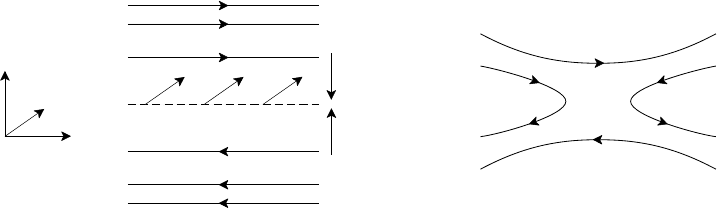
142 Resistive magnetohydrodynamics

B(y)

(a)

(b)

Fig. 5.1. Magnetic reconnection in slab plasma.

scale intermediate between τ

and τ

. Such fast reconnections taking place at

current sheets are vital for violent events like solar ﬂares on the one hand and

major disruptions in tokamaks on the other. The concept of relaxation of stressed

magnetic ﬁelds and energy release in one form or other underpins much of the

discussion in this chapter.

5.2 Magnetic relaxation and reconnection

To understand how magnetic ﬁeld changes occur in a real plasma with small but

ﬁnite resistivity let us consider the simplest model of a slab plasma, as in Fig.

5.1(a), in which the ﬁeld is slowly varying with y, decreasing in magnitude, re-

versing sign, and then increasing again. The plane (y = 0) in which B = 0is

called the neutral sheet. If the ﬁeld lines deﬁne the z-axis, the current j is parallel

to the x-axis and the Lorentz force j×B acts downwards for y > 0 and upwards for

y < 0. In ideal MHD, either these forces are opposed by a plasma pressure gradient

maintaining equilibrium or plasma and ﬁeld lines will move together towards the

y = 0 plane until these forces are in balance. However, with the introduction of

ﬁnite resistivity, no matter how small, the ﬁeld is no longer frozen into the plasma

and slippage of ﬁeld lines across the plasma allows breaking of the ﬁeld lines with

reconnection to lines of opposite polarity as shown in Fig. 5.1(b). This may happen

at various points along the neutral lines, as depicted in Fig. 5.2, giving rise to

so-called magnetic islands, i.e. sets of nested magnetic surfaces each with its own

magnetic axis. The dashed line in Fig. 5.2 is the separatrix marking the boundary

between the regions of different ﬁeld topology. The topological change takes place

because the magnetic energy associated with the magnetic islands is less than that

in the original, MHD equilibrium conﬁguration. We can readily imagine this if we

5.2 Magnetic relaxation and reconnection 143

Fig. 5.2. Magnetic islands.

think of the ﬁeld lines as stretched strings; the tension in them has been reduced

because breaking and reconnecting allows them to contract around the island axes.

The stored (potential) energy in the ﬁnal conﬁguration is less than in the original

conﬁguration. The null-points of the magnetic ﬁeld deﬁne O-points, at the axes of

the magnetic islands, and X-points, at the intersections of the separatrix.

Some dissipation is essential for any system to attain a lower energy state from

its initial state by a relaxation process and Taylor (1974) provided a mathematical

basis for this by applying a modiﬁcation of Woltjer’s theorem to plasmas with small

but ﬁnite resistivity. As discussed in Section 4.3.4, Woltjer showed that the helicity,

K =



A · B dτ , of an ideal plasma is invariant when the integral is taken over

the volume V of a closed system. It follows that K is conserved for every volume

enclosed by a ﬂux surface, i.e. every inﬁnitesimal ﬂux tube. This amounts to an

inﬁnite set of integral constraints ensuring a one-to-one correspondence between

initial and ﬁnal ﬂux surfaces. Clearly, this no longer holds in a plasma with ﬁnite

resistivity since the continual breaking and reconnecting of ﬁeld lines destroys the

identity of inﬁnitesimal ﬂux tubes. Taylor’s hypothesis states that only the helicity

associated with the total volume of the plasma is conserved. This replaces an

inﬁnite set of constraints by a single constraint and allows the system access to

lower energy states which in ideal MHD are forbidden. It means, also, that the ﬁnal

state of the plasma is largely independent of its initial conditions. Indeed a feature

of certain toroidal discharges is that after an initial, violently unstable phase, the

discharge relaxes to a grossly stable, quiescent state which depends only on a few

external parameters and not on the history of the discharge. The characteristics

of reversed ﬁeld pinches, in particular, may be interpreted on the basis of Taylor’s

hypothesis. By contrast, relaxation does not play such a prominent role in tokamaks

on account of the strong toroidal magnetic ﬁeld.

Assuming that the plasma is contained by perfectly conducting walls the only

ﬂux surface that retains its identity is the plasma boundary. Taylor argued, there-

144 Resistive magnetohydrodynamics

fore, that the energy should be minimized subject to the single constraint of con-

stant total magnetic helicity, i.e.



A · B dτ = const.

where V

is the total plasma volume. If the plasma is almost ideal and its kinetic

energy is negligible compared with the magnetic energy (β ≈ 0) one arrives, as in

Woltjer’s theorem, at the condition for force-free ﬁelds

∇ × B = αB (5.2)

but with the fundamental difference that here α is a constant, related to K

, with the

same value on all ﬁeld lines. In view of the assumed boundary conditions (see Sec-

tion 4.3.4), a second constant determining the solution of (5.2) is the total toroidal

ﬂux. For a linear discharge with cylindrical symmetry (∂/∂θ ≡ ∂/∂z ≡ 0)) we

have from (5.2)

(r) = 0 αB

=−

α B

(rB

)

giving

+ α

= 0

This is Bessel’s equation of order zero with the result that

(r) = B

(αr ) B

(r) = B

(αr ) (5.3)

where J

and J

are Bessel functions of the ﬁrst kind of order zero and one,

respectively, and B

is the value of the magnetic ﬁeld on the axis. Since J

(x)

changes sign at x = 2.4 it follows that ﬁeld reversal will occur if, in the relaxed

state, the plasma radius a is such that αa > 2.4.

To appreciate the implications of this condition in practice it is helpful to in-

troduce two measurable quantities, the ﬁeld reversal parameter F, which is the

normalized toroidal ﬁeld at r = a, i.e.

F = B

(a)/B



where B

 denotes the average toroidal magnetic ﬁeld and the pinch parameter θ,

which represents the normalized toroidal current,

θ =

θ0

(a)

B



2ψ

αa

where ψ

is the toroidal ﬂux and we have set µ

= 1. It follows using (5.3) that

F =

αa

(αa)

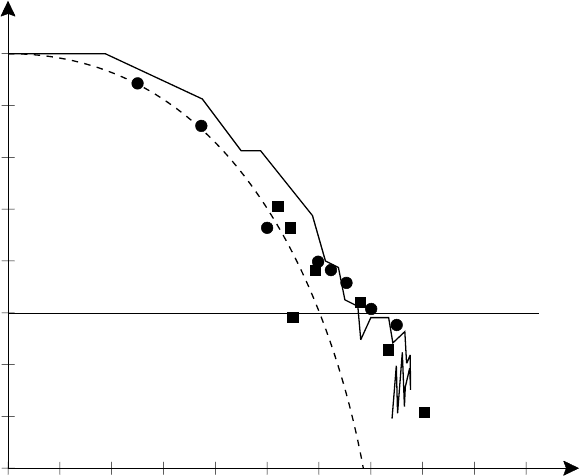
5.2 Magnetic relaxation and reconnection 145

–0.6

Fig. 5.3. Measured (F–θ) characteristics:



, Zeta; •, HBTX; ——, Di Marco; and the

theoretical curve (dashed line).

Figure 5.3 plots F as a function of θ . We see that as the current increases, B

(a)

decreases and changes sign at θ = 1.2, corresponding to ﬁeld reversal. Figure 5.3

also shows a measured (F –θ) characteristic (Di Marco (1983)) which, while

broadly in agreement, lies above the theoretical curve. The discrepancy between the

characteristics showing less pronounced ﬁeld reversal in practice than predicted, is

generally attributed to the behaviour of the current density in the boundary region.

A relaxed state with α = j · B/B

constant is inconsistent with the physical

boundary condition j = 0 at the plasma edge. From Fig. 5.3 we see also that

the current does not increase beyond θ ∼ 1.5 (i.e. αa ∼ 3) which is in agreement

with the predicted value (αa = 3.1). Further increasing the voltage does not result

in higher current. Data from a high-beta toroidal pinch experiment (HBTX) and

from Zeta, analysed by Bodin and Newton (1980), provide additional support for

the relaxation hypothesis.

5.2.1 Driven reconnection

A distinction may be drawn between spontaneous and driven reconnection. What

has been considered so far is the relaxation of plasma in reversed ﬁeld pinches to

146 Resistive magnetohydrodynamics

a state of lower energy by magnetic ﬁeld reconnection. Examples of spontaneous

reconnection arising in other magnetically contained plasmas crop up later in this

chapter, as for instance in Section 5.3.1, where we shall see that reconnection is

responsible for the tearing mode instability. However a less benign form of recon-

nection, sometimes referred to as driven reconnection, may take place. The most

dramatic events of this kind occur in nature where plasmas collide, as happens in

solar ﬂares and when the solar wind strikes the Earth’s magnetosphere. It is possible

to distinguish the two types of magnetic reconnection by a qualitative argument. In

the spontaneous case if we suppose that a current sheet is present initially then

referring to (5.1) we may use the Lundquist number as an index of the spontaneous

reconnection rate M

where

= S

−1

 1

The need for fast reconnection ﬁrst became evident in attempts to explain the

explosive onset of solar ﬂares. Through fast reconnection the magnetic ﬁeld can

change its morphology and so release energy. The importance of neutral points

at which the ﬁeld vanishes was ﬁrst realized by Giovanelli (1947) and stressed

by Dungey (1953) who showed that rapid dissipation of the magnetic ﬁeld was

possible at X-type neutral points. Sweet (1958) noted that energy release from a

magnetic ﬁeld requires the ﬁeld to be stressed in some way and the model used

to represent this was one in which oppositely directed ﬁelds collide. Figure 5.4

shows schematically magnetic ﬁelds being pushed together by ﬂows into a narrow

region. In the ﬂow regions the resistivity is low and hence the magnetic ﬁeld is

frozen in the ﬂow. The two regions are separated by a current sheet since the

reversal of the magnetic ﬁeld B requires a current to ﬂow in the thin layer sep-

arating them. Within this layer resistive diffusion plays a key role. As the two

regions come together the plasma is squeezed out along the ﬁeld lines allowing

the ﬁelds to get closer and closer to the neutral sheet. At some stage the ﬁeld lines

break and reconnect in a new conﬁguration at a magnetic null-point, X. The large

stresses in the acutely bent ﬁeld lines in the vicinity of the null-point result in a

double-action magnetic catapult that ejects plasma in both directions, with velocity

of O(v

). This in turn allows plasma to ﬂow into the reconnection zone from the

sides.

This model was later developed by Parker (1963) and is generally referred to as

the Sweet–Parker model. A simple quasi-static argument using momentum balance

shows that the plasma is ejected at the Alfv

en velocity, v

. Denoting the length of

the current sheet by 2L and the thickness by 2d, mass conservation dictates that

uL = v

d where u is the plasma ﬂow speed in the direction normal to B. Under

steady state conditions the rate at which magnetic ﬂux is convected towards the