Boyd T.J.M., Sanderson J.J. The Physics of Plasmas

Подождите немного. Документ загружается.

4.4 Solar MHD equilibria 107

buoyancy

tension

section of

photosphere

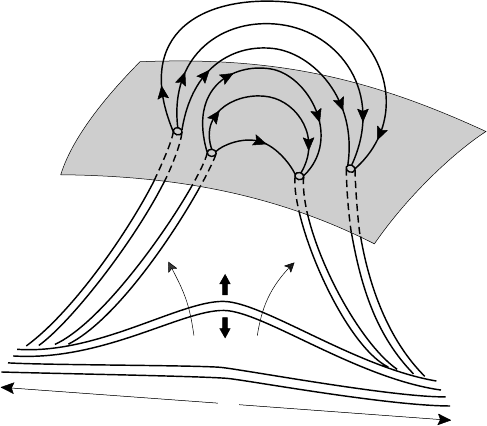
Fig. 4.21. Buoyancy of ﬂux tubes from the convective zone to the surface of the Sun.

where  ≡ k

T/mg is the local scale height, and the ﬂux tube will rise through

the photosphere in response to it. In general a ﬂux tube rising in this way will not

remain horizontal (see Fig. 4.21) and once some curvature develops the buoyancy

will be countered by magnetic tension along the ﬁeld lines. Provided the length

of the ﬂux tube L > 2 magnetic buoyancy forces continue to act. Parker also

showed that raising a section of a long ﬂux tube will result in a ﬂow of plasma

from that section and so serve to enhance buoyancy.

The simplicity of the magnetic buoyancy concept set alongside evidence that

the background magnetic ﬁeld of the Sun appears as a distribution of isolated ﬂux

tubes is appealing though the model needs modiﬁcation to allow for realities such

as turbulence in the convective zone and the fact that solar rotation distorts ﬂux

tubes. At a deeper level one might question where ﬂux tubes come from in the ﬁrst

place. There are no grounds for supposing that the magnetic ﬁelds generated by dy-

namo action would produce long ﬂux tubes. It would seem that some mechanism,

possibly an instability, is needed to cause the ﬁelds generated deep in the convective

zone to fragment and concentrate. Further questions are posed by observations of

the apparent mutual attraction of magnetic knots and their coalescence leading to

the formation of sunspots. Many issues affecting magnetic buoyancy are discussed

in detail by Parker (1979), Priest (1987) and Hughes (1991).

108 Ideal magnetohydrodynamics

4.5 Stability of ideal MHD equilibria

Having discussed various plasma equilibria we now turn to a consideration of

their stability. The most striking feature of observations of Z-pinch dynamics is a

tendency for the plasma to twist and wriggle prior to breaking up. Z-pinches appear

to be inherently unstable dynamical systems. Furthermore, we have seen that there

is no toroidal equilibrium without a poloidal component of the magnetic ﬁeld.

Toroidal conﬁgurations must therefore have a non-zero toroidal current which may

then act as a source of free energy for the development of instabilities. The question

of stability is of vital importance for plasma containment and for explaining natural

phenomena like solar ﬂares, sunspots and prominences.

The terms stable, unstable describe the behaviour of dynamical systems in

equilibrium towards small perturbations of the system. If a perturbation causes

forces to act on the system tending to restore it to its equilibrium conﬁguration, the

system is said to be in stable equilibrium (with respect to the class of perturbations

considered). If, on the other hand, the system tends to depart further and further

from the equilibrium conﬁguration as a result of the perturbation, it is in unstable

equilibrium.

In general, plasma instabilities may be broadly categorized as macroscopic or

microscopic. The ﬁrst class involves the physical (spatial) displacement of plasma

and may be discussed within the framework of the MHD equations. Microscopic

instabilities need to be described on the basis of kinetic theory since they arise

from changes in the velocity distribution functions and this information is lost in

the MHD description. Although microscopic instabilities can be very important,

usually they are less catastrophic than MHD instabilities and so the latter are

normally one’s ﬁrst concern. Likewise, ideal MHD stability may be regarded as

a ﬁrst step towards MHD stability because the introduction of dissipation allows

slippage between ﬂuid and ﬁeld which usually facilitates instability; if this is so

we may expect that an ideal MHD stability condition is necessary but not always

sufﬁcient for maintaining the equilibrium.

In this section the ideal MHD stability of some static conﬁgurations is discussed.

The investigation of ideal MHD stability can be approached in a number of ways.

We emphasize at the outset that we shall conﬁne our attention to linear stability

analyses. Within a linear framework stability considerations can be approached

from the point of view of an initial value problem or alternatively, from a normal

mode perspective. The ﬁrst determines the evolution in time of a prescribed initial

perturbation and in so doing provides more information than is needed to answer

the question of stability. The normal mode approach leads to an eigenvalue equa-

tion. Since in practice most stability problems can only be resolved numerically,

the normal mode route generally offers advantages over solving the initial value

4.5 Stability of ideal MHD equilibria 109

problem. Here we shall describe both methods, starting with the initial value prob-

lem.

Since we are concerned with small departures from equilibrium we can apply

perturbation theory to the ideal MHD equations in Table 3.2. We write

ρ(r, t) = ρ

(r) + ρ

(r, t)

u(r, t) = u

(r) + u

(r, t) = u

(r, t)

P(r, t ) = P

(r) + P

(r, t)

B(r, t) = B

(r) + B

(r, t)











(4.55)

where the subscripts 0 and 1 denote equilibrium and perturbation values, respec-

tively, and we have put u

= 0 since the equilibrium is static. Ignoring products of

the perturbations gives, to zero order, the equilibrium equation

∇P

= (∇ × B

) × B

(4.56)

and, to ﬁrst order,

∂ρ

∂t

=−u

· ∇ρ

− ρ

∇ · u

(4.57)

∂u

∂t

=−∇P

(∇ × B

) × B

(∇ × B

) × B

(4.58)

∂B

∂t

= ∇ × (u

× B

) (4.59)

∂ P

∂t

=−u

· ∇P

− γ P

∇ · u

(4.60)

In deriving (4.60) we have used (4.57) to simplify the ﬁnal expression.

Now since u

(r, t) is the only time-dependent variable on the right-hand sides

of (4.57), (4.59) and (4.60) we may integrate them partially with respect to time.

It is convenient to choose initial conditions such that the constants of integration

(r, 0), B

(r, 0) and P

(r, 0) are all zero; this simply means that we start at

the equilibrium conﬁguration and disturb it dynamically by means of a non-zero

(r, 0). The integrated equations are

(r, t) =−ξ(r, t) · ∇ρ

− ρ

∇ · ξ(r, t) (4.61)

(r, t) = ∇ × (ξ(r, t) × B

(r)) (4.62)

(r, t) =−ξ(r, t) · ∇P

(r) − γ P

(r)∇ · ξ(r, t) (4.63)

where the displacement vector

ξ(r, t) ≡



(r, t



)dt



(4.64)

110 Ideal magnetohydrodynamics

From (4.64)

∂ξ

∂t

= u

(r, t) (4.65)

so that the initial conditions on ξ are

ξ(r, 0) = 0 ∂ξ(r, 0)/∂t = u(r, 0) = 0 (4.66)

We have written the integral of (4.57) for future reference but it may be noted

that ρ

no longer appears in the remaining equations (4.58)–(4.60) which form a

closed set. Thus, substituting (4.62) and (4.63) in (4.58) gives

∂

∂t

= F(ξ(r, t)) (4.67)

where

F(ξ) = ∇(ξ · ∇ P

+ γ P

∇ · ξ) +

(∇ × B

) × [∇ × (ξ × B

)]

{[∇ × ∇ × (ξ × B

)] × B

} (4.68)

The equilibrium conﬁguration deﬁnes ρ

, P

, and B

so that (4.67), together with

appropriate boundary conditions and the initial values (4.66), determines the dis-

placement vector ξ and hence the time evolution of ρ

, B

, P

and u

. This is the

initial value solution of the linear stability problem.

Finding the normal mode solution is less onerous. We now assume that we may

separate the space and time dependence of the displacement, ξ(r, t) = ξ(r)T (t ),

so that (4.67) becomes

T =−ω

−ω

ξ(r) = F[ξ(r)] (4.69)

where the separation constant is chosen as −ω

so that T (t) = e

iωt

and ξ(r, t) =

ξ(r)e

iωt

. Since F(ξ) is linear in ξ, (4.69) represents an eigenvalue problem in which

the boundary conditions determine the possible values of ω

. If these are discrete

and labelled with sufﬁx n, the general solution of (4.67) is

ξ(r, t) =



(r)e

iω

(4.70)

where ξ

(r) is the normal mode corresponding to the normal frequency ω

.One

can show from the properties of F(ξ) that for any discrete normal mode the eigen-

value ω

is real (see Exercise 4.7). It is then clear from (4.70) that if, for all the

normal frequencies, ω

> 0 then all the modes are periodic. This means that the

system oscillates about the equilibrium position. On the other hand, if at least one

4.5 Stability of ideal MHD equilibria 111

of the normal frequencies is such that ω

< 0 the corresponding normal mode will

grow exponentially and the equilibrium conﬁguration is unstable.

This property of real eigenvalues is directly related to the conservation of energy

in ideal MHD. In principle, by suitable choice of initial perturbation, one could ex-

cite each normal mode in turn. The mode can either oscillate about the equilibrium

position or the perturbation can grow continuously as the potential energy of an

unstable equilibrium position is converted to kinetic energy. Damped or growing

oscillations are not possible since these would require an energy sink or source.

Thus, ω

is either real or pure imaginary and ω

is real. This leads ultimately to the

most elegant and efﬁcient method of investigating stability, the energy principle.

It is also important for the analysis of neutral or marginal stability. In general

the transition from stability to instability takes place at ω = 0 and ω must be

calculated. In ideal MHD, however, stability boundaries are deﬁned by ω = 0

which makes their determination much easier.

4.5.1 Stability of a cylindrical plasma column

By way of illustration we apply the normal mode analysis to determine the stability

of a cylindrical plasma of length L and circular cross-section of radius a.We

assume that the equilibrium ﬁelds in the plasma and the surrounding vacuum are

= (0, 0, B

) (4.71)

and

= (0, B

(r), B

) (4.72)

respectively, where B

and B

are constants and B

(r) is the azimuthal ﬁeld due

to the current ﬂowing along the plasma column. Substituting (4.71) in (4.12) gives

j = 0 everywhere except at the edge of the plasma column and, if the total ‘skin’

current is I , it follows that

(r) =

2πr

(4.73)

Also, since j(r) = 0 (r < a), from (4.10) we see that P

is constant so that (4.69)

reduces to

−ρ

ξ(r) = γ P

∇(∇ · ξ) +

(∇ × B

) × B

(4.74)

where, for computational convenience, we have re-introduced B

using (4.62).

We are interested in perturbations with poloidal and axial periodicity so we set

ξ(r) = [ξ

(r), ξ

(r)]e

i(mθ+kz)

(4.75)

112 Ideal magnetohydrodynamics

where m and (kL/2π) take integer values. Also, to lighten the algebra we assume

that

∇ · ξ = 0 (4.76)

which infers that the plasma is incompressible. It is shown in the next section that

allowing for compressibility makes the plasma more rather than less stable so that

for considerations of stability our assumption errs on the side of caution.

The procedure is to solve (4.74) within the plasma column, together with the

ﬁeld equations in the vacuum surrounding the plasma and to apply the boundary

conditions across the plasma–vacuum interface. It is this last step that determines

the set of values of ω (the normal frequencies ω

) for which (4.70) is an acceptable

solution.

Starting with the plasma interior, it is easily seen that, on using (4.75) and (4.76),

(4.62) becomes

= ikB

ξ (4.77)

and, since P

is constant, (4.63) gives

= 0 (4.78)

On taking the divergence of (4.74) only the last term contributes giving

∇ · [(∇ × B

) × B

] = B

· (∇ × ∇ × B

) =−B

·∇

= 0

which, on using (4.77), becomes

∇

= 0

In cylindrical polar coordinates this is the Bessel equation



−





(r) = 0

for which the solution having no singularity at r = 0is

(r) = ξ

(a)

(kr)

(ka)

(4.79)

where I

is the modiﬁed Bessel function of the ﬁrst kind of order m.

Next, we use (4.77) and the radial component of (4.74) to obtain

(r) =−

ikB

− µ

ρω

)

dξ

=−

(a)

− µ

ρω

)



(kr)

(ka)

(4.80)

and, although we shall not require it explicitly, we could likewise ﬁnd ξ

(r).The

ﬁeld perturbations in the plasma column are then given by (4.77).

4.5 Stability of ideal MHD equilibria 113

In the vacuum, since j = 0, we may represent the ﬁeld perturbation by a scalar

potential

= ∇φ (4.81)

where φ takes the form φ(r)e

i(mθ+kz)

.Then∇·

= 0 shows that φ(r) satisﬁes the

same Bessel equation as ξ

(r) but here we must choose the solution which vanishes

at inﬁnity giving

φ(r ) = φ(a)

(kr)

(ka)

(4.82)

where K

is the modiﬁed Bessel function of the second kind of order m.

Finally, we apply the ideal MHD boundary conditions (3.73) and (3.74) at the

plasma–vacuum interface. The conditions are valid, of course, in both the equilib-

rium and the perturbed conﬁgurations so that zero-order terms cancel each other

out and only terms linear in perturbed quantities need be retained. Nevertheless,

this procedure requires some care because linear terms arise from the displacement

of the interface as well as directly from the perturbations. Denoting the equilibrium

position of a point on the interface by r

, its displacement is

r − r



, t



)dt



(4.83)

Comparing this with (4.64) and assuming that r − r

remains a small quantity it

is easily seen that to ﬁrst order, r − r

= ξ(r

, t)  ξ(r, t). The subtle difference

between ξ(r, t) and ξ(r

, t), which is of second order, is that (4.83) describes the

displacement of a ﬂuid element (labelled by r

) in a Lagrangian coordinate system

moving with the ﬂuid, whereas (4.64) deﬁnes a displacement vector from a ﬁxed

point r in an Eulerian coordinate system relative to a ﬁxed inertial frame. Thus, we

use the expansion

f (r, t) = f

(r, t) + f

(r, t)

 f

) + ξ · ∇ f

+ f

(r, t)

for each quantity appearing in the boundary conditions.

Keeping only ﬁrst-order terms (3.73) gives

· B

+ (ξ · ∇)

2µ

which, on using (4.71)–(4.73), (4.77), (4.78) and (4.81), becomes

ikB

(a) =



ikB

(a)



φ(a) −

(a)

(a) (4.84)

114 Ideal magnetohydrodynamics

+ n

δr

ξ + (δr . ∇)ξ

+ δr(r

)

Fig. 4.22. Interface perturbations.

Linearizing (3.74) we have

· n

+ B

· n

= 0 (4.85)

and

[

+ (ξ · ∇)

] · n

· n

= 0 (4.86)

where n

r, the radial unit vector, and n

is the perturbation in n

due to the

migration of the interface. To ﬁnd n

we note that any inﬁnitesimal displacement

δr(r

) from a point r

on the interface will remain on the interface provided

δr · n

= 0. Applying this condition on the perturbed interface we have, with

reference to Fig. 4.22,

[δr + (δr · ∇)ξ] ·(n

+ n

) = (δr · ∇)ξ

+ δr · n

= 0

and, since δr may be chosen arbitrarily, this gives

=−∇ξ

Substituting this in the boundary conditions, (4.85) is satisﬁed identically and

(4.86) becomes



dφ



r=a

− ikB

(a) −

(a)ξ

(a) = 0

4.5 Stability of ideal MHD equilibria 115

small

large

plasma

surface

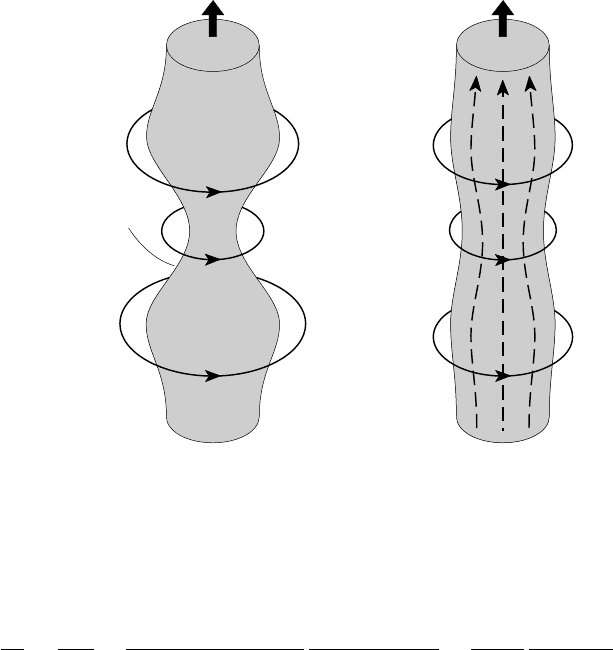
Fig. 4.23. Sausage instability.

Now we use (4.80) and (4.82) to substitute for ξ

(a) and φ



(a) and (4.84) to

eliminate the constant φ(a) obtaining the dispersion relation

−

(

+ mB

(a)/ka

)



(ka)K

(ka)

(ka)K



(ka)

−

(a)



(ka)

kaI

(ka)

(4.87)

Each term on the right-hand side of this equation is real conﬁrming that ω can be

either real or pure imaginary, i.e. there are no solutions corresponding to damped or

growing oscillations. Instability occurs if ω

< 0 and, since K



< 0 while I

, K

and I



are all positive, this requires the third term to be larger in magnitude than

the sum of the ﬁrst two.

The m = 0 case illustrates the roles of the equilibrium magnetic ﬁelds. Both the

internal and external longitudinal ﬁelds, B

and B

respectively, enhance stability

while B

has the opposite effect. This may be explained physically with reference

to Fig. 4.23, which shows an axially symmetric perturbation of the equilibrium

conﬁguration of the Z-pinch. Since B

∝ r

−1

, the external magnetic pressure on

the plasma surface is increased where the perturbation squeezes the plasma into a

neck and is decreased where the perturbation fattens the plasma into a bulge. This

gradient in the external magnetic ﬁeld causes the perturbation to grow and, without

an internal ﬁeld, the necks contract to the axis, giving a sausage-like appearance to

the plasma; hence the name sausage instability. On the other hand, the magnetic

116 Ideal magnetohydrodynamics

unstable

stable

0.5

1.0

Fig. 4.24. Marginal stability curve for sausage instability.

pressure due to the longitudinal ﬁelds is increased by the plasma perturbations

which are, therefore, resisted.

In the case that B

= 0 the condition for stability is

> B

(a)



(ka)

kaI

(ka)

(4.88)

and since I



(x)/xI

(x)<1/2 for all x there is stability for all k provided B

(a)/2. However, for given plasma pressure P

and current I , B

is bounded

above by the equilibrium pressure condition

+ B

/2µ

= B

/2µ

(4.89)

It is, therefore, somewhat more useful to write the stability condition in terms of the

‘poloidal’ β

= 2µ

(a); see (4.32). Combining (4.88) and (4.89) we have

2µ

< 1 −



(ka)

kaI

(ka)

∼



1/2 ka → 0

1 − 1/ka ka →∞

as the marginal stability condition illustrated in Fig. 4.24.

For m > 0 it is convenient to assume |ka|1 so that we may use the

approximations

(x) ≈

(x/2)

≈

(m − 1)!





−m

(|x|1)

to simplify the dispersion relation (4.87) which then reduces to

ρω

= k



(a)



−

(a) (4.90)