Boyd T.J.M., Sanderson J.J. The Physics of Plasmas

Подождите немного. Документ загружается.

4.5 Stability of ideal MHD equilibria 117

plasma

surface

Fig. 4.25. Kink instability.

Differentiating ω

with respect to k it is easily veriﬁed that the minimum value of

occurs at

k =−

(a)

a(B

+ B

)

(4.91)

and is given by

min

(a)

ρa



+ B

− m



(4.92)

Using the equation of equilibrium pressure balance

2µ

(a)

2µ

(4.93)

and (4.32) this may be written in terms of the ratio of the external ﬁeld components

(a)/B

and the ‘toroidal’ β

= 2µ

min

(a)

ρa



(m − 1)(1 + B

(a)/B

− β

) − 1

(2 + B

(a)/B

− β

)



showing that for low β

plasmas in devices with |B

|1 only the m = 1 and

m = 2 modes can become unstable.

118 Ideal magnetohydrodynamics

The unstable m = 1 mode is known as the kink instability since it arises from

the perturbation shown in Fig. 4.25. The distortion grows because the magnetic

pressure on the concave side of the kink is increased (the B

lines are closer

together), while that on the convex side is decreased (the B

lines are further apart).

Again, the action of the longitudinal ﬁelds, whether internal or external, enhances

stability since the tension in the lines of force caused by their stretching tries to

restore the pinch to its equilibrium position. The shorter the wavelength of the

perturbation the greater is the stretching of the ﬁeld lines. The balance between

the stabilizing z-components and destabilizing θ -component of the magnetic ﬁeld

leads to an important stability condition.

To investigate this we put m = 1 in (4.90) and use (4.93) to write it in the form





1 +

(a)

kaB



(a)

− β



For |B

(a)/B

|1 and β

 1, it follows from this equation that the m = 1

mode is stable for |B

| < |ka| and since |k| cannot be less than 2π/L, where

L is the length of the plasma column, the stability condition is

| < 2πa/L

In a toroidal device, where L = 2π R

, this may be written in terms of the safety

factor (4.29) as

q(a) = aB

(a)/R

(a)>1 (4.94)

a result known as the Kruskal–Shafranov stability criterion. It says that the ratio

of toroidal to poloidal magnetic ﬁeld must exceed the aspect ratio R

/a. In (4.94)

we have implicitly extrapolated the Kruskal–Shafranov condition to the case of a

diffuse pinch with variable B

rather than the sharp-edged plasma which was the

subject of our calculation. In fact, the same result can be obtained by a simple

physical argument due to Johnson et al. (1958). We consider an m = 1 helical

perturbation of the plasma such as that shown in Fig. 4.25 and we examine the dis-

placement of a ﬁeld line by inspecting two cross-sections one-quarter wavelength

apart as shown in Fig. 4.26. If the displacement vector ξ is horizontal at the ﬁrst

cross-section it will be vertical at the second and if the pitch of B

is such that the

angle of rotation θ

>π/2 then the vertical (downwards) displacement of the ﬁeld

line due to the perturbation means that the angle of rotation has increased. This in

turn implies that the perturbation has increased B

relative to B

, thereby perturbing

the magnetic pressure balance such as to accelerate the downward displacement of

the plasma. It is easy to see that if θ

<π/2 the angle of rotation is decreased by

the perturbation, so B

is decreased relative to B

and growth of the perturbation

4.6 The energy principle 119

equilibrium

configuration

X-section

> π/2

< π/2

= π/2

ξ ξ

= π/2

displaced

X-sections

+ θ

< θ

+ θ

> θ

helical

displacements

Fig. 4.26. Illustration of Kruskal–Shafranov stability criterion for the kink instability. The

equilibrium conﬁguration on the left shows the π/2 rotation of a magnetic ﬁeld line on

traversing a quarter wavelength. The cross-sections on the right show the result of imposing

a kink displacement ξ which is initially horizontal but subsequently vertical due to the π/2

rotation.

is resisted. The stability condition is therefore ι/4 <π/2 at the boundary of the

plasma and from (4.29) this gives (4.94).

The Kruskal–Shafranov criterion, by restricting B

(a), sets a limit on the

toroidal current that may be safely driven through the plasma. It is for this reason

that a tokamak has a small ratio of poloidal to toroidal ﬁeld component.

Tokamaks are also low β devices. This second restriction is related to the un-

favourable curvature of the poloidal ﬁeld B

with respect to the plasma. Whenever

the external ﬁeld (the ﬁeld containing the plasma) is concave towards the plasma,

any ripple on the plasma will tend to grow for the same reasons that the sausage and

kink perturbations grow. Containment of these so-called ballooning instabilities

restricts β, as discussed later in Section 4.7.2. Conversely, containing ﬁelds which

are convex towards the plasma tend to smooth out ripple perturbations.

4.6 The energy principle

So far, in discussing the stability of equilibria, we have progressed from an initial

value problem to a normal mode analysis, this being made possible by the lin-

earization which led to (4.67) in which only ξ(r, t) is time dependent. The role

of the initial values is merely to determine the mixture of the normal modes in a

particular solution and this is of secondary importance when one’s main interest

is stability; in these circumstances the ‘convenient’ choice of initial conditions

in the integrals (4.61)–(4.63) is not a serious loss of generality. Nevertheless, a

120 Ideal magnetohydrodynamics

normal mode analysis still involves signiﬁcant effort as we have seen from our

relatively simple example of a sharp-edged, cylindrical plasma. Investigating the

stability of more realistic plasmas and geometries normally is only possible by

numerical analysis. If, however, one merely wants to answer the question ‘Is the

equilibrium conﬁguration stable?’ there is an even more direct approach based on

energy considerations.

Since the ideal MHD equations are dissipationless they conserve energy and a

stable equilibrium conﬁguration must correspond to a minimum in the potential

energy W . This is the physical basis of the energy principle which states that if

there exists a displacement ξ for which the change in potential energy δW < 0 the

equilibrium is unstable.

To ﬁnd an expression for δW we note that since the equilibrium is static the

(change in) kinetic energy K is

integrated over the whole plasma volume

K (

ξ,

ξ) =



ξ ·

ξ dr =−



ξ · ξ dr



ξ · F(ξ) dr (4.95)

by (4.69). Thus, by conservation of energy

δW (ξ, ξ) =−



ξ · F(ξ) dr (4.96)

From (4.95) and (4.96) we may write

= δW (ξ, ξ)/K (ξ, ξ) (4.97)

which is the variational formulation of the linear stability problem. Given that the

operator F(ξ) is self-adjoint†, that is



η · F(ξ) dr =



ξ · F(η) dr (4.98)

for any allowable displacement vectors ξ and η, it is easy to show (see Exer-

cise 4.7) that any ξ for which ω

is an extremum is an eigenfunction of (4.69) with

eigenvalue ω

. This establishes the equivalence of the variational principle and

the normal mode analysis. But in practice it is analytically and computationally

much easier to investigate stability via the variational principle. One chooses a

trial function ξ =

, where the ψ

are a suitable set of basis functions,

and minimizes δW with respect to the coefﬁcients a

subject to the normalization

condition

K (ξ, ξ) = const. (4.99)

† The direct proof of (4.98) is rather lengthy (see Freidberg (1987)).

4.6 The energy principle 121

If δW < 0 the equilibrium is unstable and the variational principle guarantees that

a lower bound for the growth rate γ of the instability is (−δW/K )

1/2

The energy principle goes a stage further in that one is not restricted to the

normalization condition (4.99). Often, great analytical simpliﬁcation is achieved

by choosing some other normalization condition. Minimization of δW with the

result δW < 0 then indicates instability but information on the growth rate is lost

since K is unknown. Each step from initial value problem through normal mode

analysis and variational principle to energy principle brings analytical and compu-

tational simpliﬁcation at the expense of detailed knowledge, from full solution of

the evolution of a linear perturbation to mere determination of the stability of the

equilibrium. Since MHD instabilities tend to be the fastest growing and the most

catastrophic (bulk movement of the plasma) the stability question is usually all one

needs answer. Furthermore, δW may be written in a form that gives good physical

insight into the cause of instability. The energy principle is, therefore, within the

limits of ideal MHD, very effective and widely used.

Returning to (4.96), with F(ξ) given by (4.68), it is straightforward, if tedious,

to recast δW in a more useful and illuminating form; the details are left as an

exercise (see Exercise 4.8). The objective is to express δW as the sum of three terms

representing the changes in potential energy within the plasma (δW

), the surface

(δW

) and the vacuum (δW

). Using vector identities one expresses the integrand

ξ · F(ξ) as a sum of divergence terms and scalar functions. Then, using Gauss’

theorem, the integral of the divergence terms is converted to an integral over the

surface of the plasma. In the surface integral the boundary condition (3.73) is used,

thereby introducing the vacuum magnetic ﬁeld. From a practical point of view this

is a most important step because the boundary condition is now incorporated in the

energy principle and there is no need to ﬁnd trial functions obeying the boundary

condition, which is a cumbersome constraint on the use of the energy principle in

its original form. Next, boundary condition (3.73) is used to eliminate the tangen-

tial component of ∇(P + B

/2µ

) in the surface integral; since (3.73) holds all

over the surface the tangential component of the gradient must be continuous and

hence

× ∇(P + B

/2µ

)]

= 0 (4.100)

Finally, using Gauss’ theorem again, part of the surface integral is converted to a

volume integral over the vacuum. The result is

δW = δW

+ δW

(4.101)

122 Ideal magnetohydrodynamics

where

δW



/µ

− ξ · (j

× B

) − P

(∇ · ξ)]dr (4.102)

δW



(ξ · n

)

[∇(P

+ B

/2µ

)]

· dS (4.103)

δW



(

/2µ

) dr (4.104)

and the integrals are taken over the plasma, surface, and vacuum, respectively.

The three terms in δW

are, respectively, the increase in magnetic energy, the

work done against the perturbed j×B force and the change in internal energy due to

the compression (or expansion) of the plasma. The surface energy δW

is the work

done by displacing the boundary. If there is no surface current the total pressure

gradient is continuous across the boundary and δW

= 0; likewise, δW

= 0

if the boundary is ﬁxed (ξ · n

= 0). The vacuum contribution δW

is simply

the increase in the energy of the vacuum ﬁeld. This also vanishes if ξ · n

= 0

since there is no perturbation of the vacuum ﬁeld. For ﬁxed boundary problems,

therefore, δW = δW

. Instabilities may be classiﬁed as internal (ﬁxed boundary)

or external (free boundary) modes.

After further manipulation (see Exercise 4.8) δW

can be expressed in the form

δW



1⊥

/µ

+ (B

/µ

)(∇ · ξ

⊥

+ 2ξ

⊥

· κ)

+ γ P

(∇ · ξ)

− 2(ξ

⊥

· ∇P

)(κ · ξ

⊥

) − j



(ξ

⊥

× b) · B

1⊥

]dr (4.105)

where κ = (b · ∇)b is the curvature of the equilibrium magnetic ﬁeld B

= B

and vector quantities have been separated into parallel and perpendicular compo-

nents relative to b, i.e. X = X



b+X

⊥

. The ﬁrst three (positive) terms in the integral

represent the potential energy associated with the shear Alfv

en wave, the compres-

sional Alfv

en wave, and the sound wave, respectively. We show in Section 4.8 that

these are the three natural wave modes supported by an ideal MHD plasma. It is

also clear from this form of δW

that compressibility (∇·ξ = 0) is stabilizing, so it

is often assumed for simplicity that the plasma is incompressible on the understand-

ing that this is a ‘worst case’ assumption and any necessary correction is favourable

to stability. The only possible destabilizing terms are the last two. The instabilities

arising from these are said to be pressure-driven and current-driven, respectively,

although, since ∇ P

= j

0⊥

×B

, both types are driven by the energy in the current

but by different components. This distinction is also used to classify ideal MHD

instabilities. The kink instability is an example of the (parallel) current-driven kind

so instabilities in this class are known as kink instabilities. The pressure-driven

4.6 The energy principle 123

modes are called interchange instabilities for reasons that will become clear when

we discuss them in Section 4.7.

4.6.1 Finite element analysis of ideal MHD stability

Practical determination of ideal MHD stability on the basis of the energy principle

has to be done computationally. Whereas codes that use ﬁnite difference methods

have to ensure that the energy-conserving properties of MHD equilibria reﬂected

in the self-adjointness of the operator F(ξ) are preserved by the difference scheme,

an alternative approach, the ﬁnite element method (FEM), has an advantage in that

it appeals directly to F(ξ), thus ensuring that energy conservation is built into the

numerics. The FEM method was developed for the stress analysis of structures

and was ﬁrst applied to problems of MHD stability independently by Takeda et al.

(1972) and by Boyd, Gardner and Gardner (1973), who analysed the stability of a

cylindrical tokamak. Subsequently, the approach was generalized and FEM codes

were developed to describe toroidal conﬁgurations.

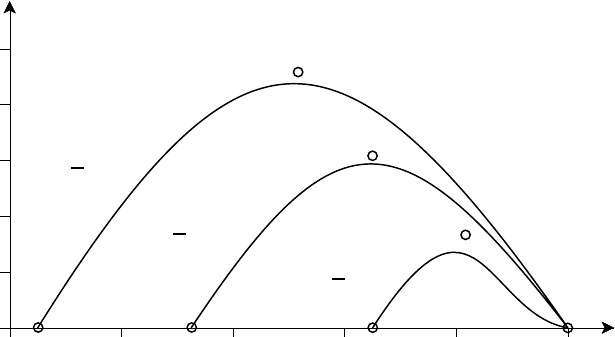
Normalized growth rates for the helical m = 2 mode in a plama column with

free boundary were determined and compared with values obtained by Shafranov

(1970) from an analysis valid for small values of the axial wavenumber k. The vac-

uum region is deﬁned by a < r < b. Figure 4.27 shows the computed normalized

growth rate as a function of nq(a) for k = 0.2 and three values of the ratio a/b. The

0.5

0.4

0.3

0.2

0.1

1.0 1.2 1.4 1.6 1.8 2.0

0.5

0.75

0.9

nq(a)

norm

Fig. 4.27. Square of normalized growth rates versus nq(a) for helical m = 2 mode in

plasma column with free boundary. The circles indicate Shafranov’s analytical results (after

Boyd, Gardner and Gardner (1973)).

124 Ideal magnetohydrodynamics

range of the instability coincides exactly with the Shafranov range (see Biskamp

(1993))

m − 1 +





< nq(a)<m (4.106)

The behaviour of growth rates as a function of nq(a) shows good agreement with

Shafranov’s theoretical result.

4.7 Interchange instabilities

Since interchange instabilities are pressure-driven they are essentially hydrody-

namic. As an example consider a case where a ﬂuid of density ρ

lies in a horizontal

layer over one of density ρ

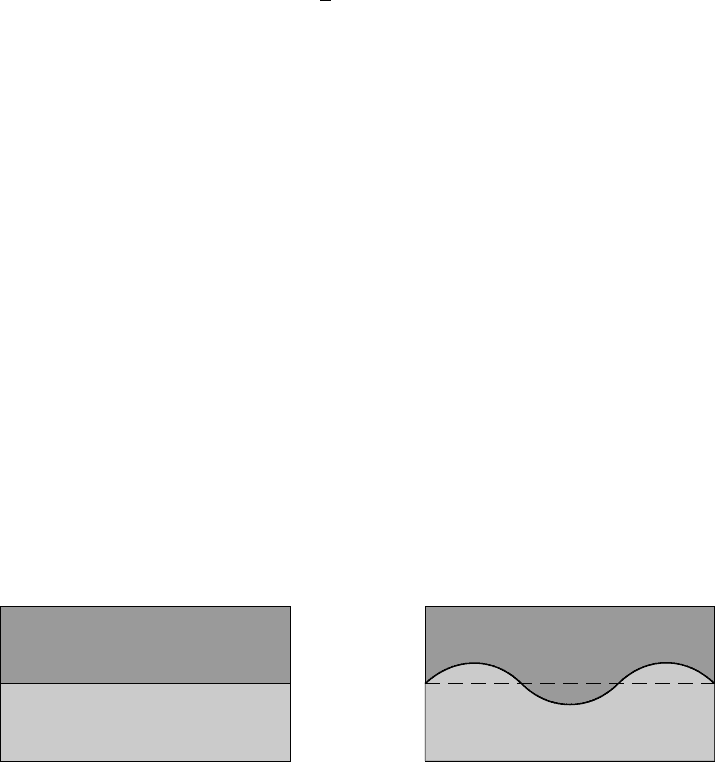
as shown in Fig. 4.28(a). Now let us perturb the

equilibrium by rippling the boundary layer. We may think of the ripple arising

from the interchange of neighbouring ﬂuid elements as suggested by Fig. 4.28(b).

The ﬂuid element of density ρ

has moved downwards with consequent loss of

gravitational potential energy while the opposite is true of the ﬂuid element of

density ρ

. Clearly, the net change in potential energy δW has the same sign as

(ρ

− ρ

) and it follows that the equilibrium is stable if and only if ρ

≥ ρ

. This

comes as no surprise; it is intuitively obvious that the only stable equilibrium is

to have the denser ﬂuid supporting the less dense. The instability that arises when

<ρ

is called the Rayleigh–Taylor instability. In a non-ideal ﬂuid the increase

in surface tension due to the stretching of the boundary provides a stabilizing effect

and prevents the growth of the instability for perturbations with wavelengths below

a certain critical value.

(a) (b)

Fig. 4.28. Rippled boundary layer between ﬂuids of differing densities.

4.7.1 Rayleigh–Taylor instability

Kruskal and Schwarzschild (1954) showed that an MHD analogue of the Rayleigh–

Taylor instability arises when a plasma is supported against gravity by a magnetic

4.7 Interchange instabilities 125

4.37a

4.37a4.37a

4.37a

B B

g =

–

∇

(a)

(b)

Fig. 4.29. Boundary perturbations for ﬁeld lines (a) perpendicular and (b) parallel to the

perturbation.

ﬁeld. A simple illustration of the origin of the instability can be constructed by

supposing that the ﬁeld lines are straight and perpendicular to the perturbation, as in

Fig. 4.29(a). We may think of the perturbation as brought about by the interchange

of ﬂux tubes and elongated ﬂuid elements with no change in magnetic energy since

there is no bending of the ﬁeld lines. The ﬂuid elements, on the other hand, have

lost potential energy; hence, the perturbations will grow and the equilibrium is

unstable.

Although gravity is of no signiﬁcance in laboratory plasmas any other accel-

eration of the plasma may take on the role of gravity. For example we saw in

Section 2.4.2 that particles moving in curved magnetic ﬁelds feel a centrifugal

force which acts like an equivalent gravitational force.

To discuss the instability quantitatively we consider the gravitational case in

plane geometry. This minimizes the algebra without losing the essential physics.

The ﬁrst point to note is that had we taken the ﬁeld lines parallel to the perturba-

tion in our simple illustration they would have been bent by the perturbation as

indicated in Fig. 4.29(b), thereby increasing the magnetic energy and providing a

stabilizing effect akin to that of surface tension in the hydrodynamic case. Clearly,

perturbations parallel to the ﬁeld maximize this stabilizing effect but one cannot

assume perturbations will not arise in a direction perpendicular to the ﬁeld for

which there is no stabilizing effect. However, by introducing magnetic shear we

can make sure that for any given mode with propagation vector k this least stable

condition, k · B = 0, is restricted to speciﬁc layers and does not occur throughout

the plasma. Thus, in our analysis we want to allow for arbitrary orientation of k

to B and vertical variation of the direction of B. Without loss of generality, we

may choose coordinates such that the y axis is vertical and the z axis is parallel to

k, the direction of propagation of the mode under investigation. Then the equilib-

rium magnetic ﬁeld B

(y) = [B

(y), 0, B

(y)] and the gravitational acceleration

g = (0, −g, 0).

With these preliminaries we now proceed to a normal mode analysis of the MHD

Rayleigh–Taylor instability in which the perturbation

ξ(r, t) = [0,ξ

(y), ξ

(y)]e

i(kz−ωt)

126 Ideal magnetohydrodynamics

and, for the reasons discussed earlier, we impose the incompressibility condition

∇ · ξ =

dξ

+ ikξ

= 0 (4.107)

The dispersion relation is obtained from (4.67) but the inclusion of the gravitational

force ρg in the equation of motion leads to an extra term ρ

g in F(ξ) which, on

using (4.61) and (4.107), becomes

F(ξ) = ∇(ξ · ∇ P

) − ξ · ∇ρ

g +

(∇ × B

) × [∇ × (ξ × B

)]

{[∇ × ∇ × (ξ × B

)] × B

} (4.108)

Remembering that equilibrium variables vary only with y, we ﬁnd for the y and z

components of (4.67)

(ξ



) − gξ



ikB



· ξ)

(ikB

· ξ



− B

· B



− B

· B



+ ikB



· ξ − B



· B



) (4.109)

= ikξ



−

· ξ) −

ikξ

· B



)

(4.110)

Substituting for ξ



from (4.110) and for ξ

from (4.107) then gives



−

(k · B

)



dξ



− k



−

(k · B

)



− k

dρ

= 0

(4.111)

This differential equation contains all the information we need to discuss the

Rayleigh–Taylor instability. For example, the hydrodynamic case is obtained by

putting B

= 0 and assuming ρ



= 0 except at y = 0, this being the boundary

between the two ﬂuids, labelled 1 for y > 0and2fory < 0. Then in both ﬂuids

(4.111) is



− k

= 0

with solutions

(y) =



(0)e

−ky

y > 0

(0)e

y < 0

Now, integrating (4.111) over the interval −<y < + and letting  → 0weget

−(ρ

+ ρ

)kω

(0) − k

g(ρ

− ρ

)ξ

(0) = 0