Boyd T.J.M., Sanderson J.J. The Physics of Plasmas

Подождите немного. Документ загружается.

4.3 Static equilibria 87

Now from (4.17)

j =

(rB) (4.24)

which integrates to give

(rB)

r=a

= µ



jr dr

and, on deﬁning the total current I ﬂowing in the plasma column by

I =



2πrj dr (4.25)

we get



rPdr =

8π

Assuming quasi-neutrality, Zn

(r) = n

(r), and uniform ion and electron temper-

atures, we may substitute

P(r) = n

(r)k

+ n

(r)k

= n

(r)k

+ T

/Z ) (4.26)

to obtain

= 8π k

+ T

/Z )N

/µ

(4.27)

where



2πrn

(r)dr (4.28)

is the number of electrons per unit length (electron line density) of the plasma

column. Equation (4.27), known as Bennett’s relation, determines the total current

required for containment of a plasma of speciﬁed temperature and line density.

(Note, however, that this analysis assumes a stable conﬁguration; in fact, the Z-

pinch, as we shall see in Section 4.5.1, is highly unstable.)

A device in which the ﬁeld lines wind around the axis in a helical path is called

a screw pinch. The rate at which the ﬁeld lines rotate about the axis of the cylinder

is an important parameter for equilibrium and stability. Referring to Fig. 4.6, this

can be measured by dθ/dz and this in turn is determined from the equation for the

magnetic ﬁeld lines

r dθ

(r)

88 Ideal magnetohydrodynamics

(a) (b)

Fig. 4.6. Screw pinch geometry.

The total angle of rotation for a cylinder of length 2π R

(the one-dimensional

equivalent of a torus of major radius R

) is called the rotational transform and is

denoted by

ι(r ) =



2π R



dθ



dz =

2π R

(r)

A related parameter, the signiﬁcance of which will be seen when we consider

stability in the next section, is the MHD safety factor

q(r) = 2π/ι(r) = rB

(r)/R

(r) (4.29)

The pitch of a ﬁeld line is deﬁned as the length of its projection on the axis in one

complete rotation about the axis so that it is given by



2π



dθ



dθ =

2πrB

(r)

4π

ι(r )

In the screw pinch the ability to manipulate two proﬁles, B

(r) and B

(r), in-

stead of only one gives much greater ﬂexibility in controlling the various physical

parameters which inﬂuence stability and other conditions necessary for contain-

ment. One such parameter is the safety factor, while another is the plasma β for

which one needs an optimum value between high β to achieve large nτ (to satisfy

the Lawson criterion) and low β because of instability thresholds. Multiplying

(4.18) by πr

and integrating from 0 to a gives



2πrPdr +



2πr



2µ



dr − πa



(a) + B

(a)

2µ



= 0

4.3 Static equilibria 89

which may be written as

P+B

/2µ

−

(a)

2µ

−

(a)

2µ

= 0 (4.30)

where

X =

πa



2πrX(r) dr

is the average value of X (r) over a cross-section of radius a. Deﬁning

β=

2µ

P

(a)

(4.31)

and similarly the corresponding ‘poloidal’ and ‘toroidal’ parameters as

2µ

P

(a)

2µ

P

(a)

(4.32)

we may write (4.30) as

β

= 1 +

B



2µ

P

(4.33)

This equation shows the ﬂexibility of the screw pinch. Clearly, β can take

values in the range 0 ≤β≤1. Furthermore, any particular value can be achieved

given the range of choices for β

and β

. This contrasts sharply with theta- and

Z-pinches where β is given by β

and β

respectively and, in the latter case,

β=β

= 1. Note from the ﬁrst equality in (4.33) that whenever β

and β

differ

in magnitude, β is given approximately by the smaller of these parameters.

4.3.2 Toroidal conﬁgurations

So far the discussion of plasma conﬁnement has concentrated entirely on radial

containment. There is nothing to prevent the plasma from ﬂowing freely along the

ﬁeld lines and in cylindrical discharges plasma will be lost through the ends of the

device unless something is done to prevent this. The obvious answer is to bend the

cylinder round into a torus so that, rather than ﬂowing out of the ends, the plasma

ﬂows round and round the device. This, however, introduces a second equilibrium

constraint, known as the toroidal force balance.

Qualitatively, we can see how the problem arises by picturing what happens to

the magnetic surface surrounding the initially cylindrical plasma as it is bent into

a torus. There results a net outward force on the toroidal plasma which has two

components, one due to the plasma pressure and the other due to the magnetic

pressure.

90 Ideal magnetohydrodynamics

< pS

plan view

X-section

> S

< S

cylinder

torus

Fig. 4.7. Net outward force in a torus due to plasma pressure.

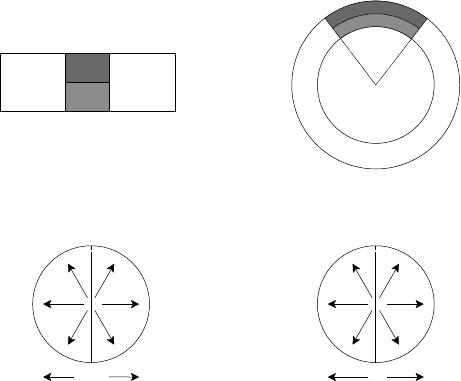
The ﬁrst of these is akin to the force in an inﬂated tyre and is simply due to the

fact that the total surface area of the outer half of the tube, or in our case magnetic

surface, is greater than that of the inner half, while the pressure is constant over

the (isobaric) surface so that the force outwards is greater than the force inwards.

This is demonstrated schematically in Fig. 4.7 by plan and cross-sectional views of

cylindrical and toroidal conﬁgurations. Segments of equal area (S) in the cylinder

are stretched on the outer surface S

(> S) and compressed on the inner surface

(< S) of the torus.

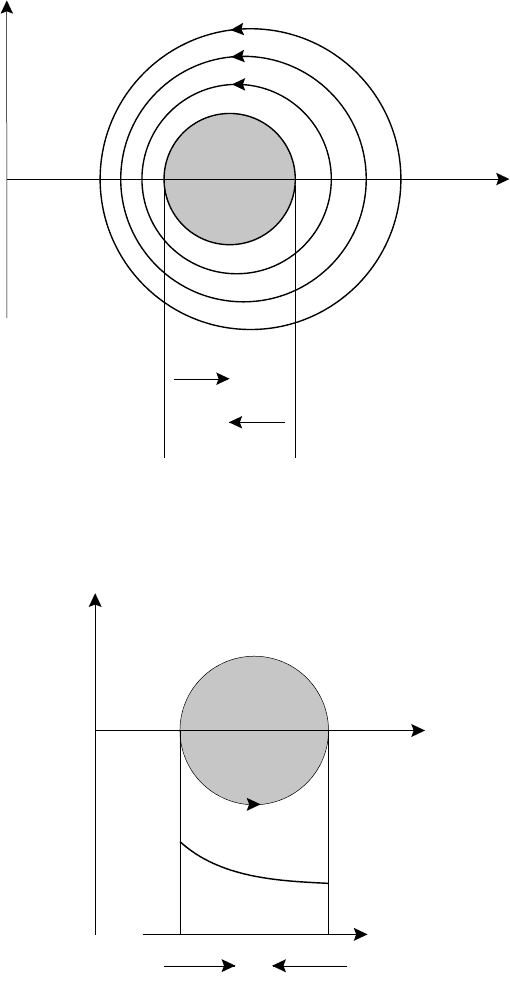
The other force involving the magnetic ﬁeld is best understood by considering

poloidal and toroidal ﬁelds separately. When there is only a poloidal ﬁeld (the

case, illustrated in Fig. 4.8, of bending a Z-pinch into a torus) this force is similar

to the outward force experienced by a current-carrying circular loop. Conservation

of magnetic ﬂux generated by the current means that ﬁeld lines are more densely

packed inside the loop than outside so that the ﬁeld strength is greater inside giving

a net j × B force radially outwards.

For the purely toroidal ﬁeld consider the simple case, shown in Fig. 4.9, of no

initial internal ﬁeld. Then the current ﬂows in a thin skin at the plasma surface

and the external ﬁeld, generated by the current I

in the toroidal ﬁeld coils, is

4.3 Static equilibria 91

j x B

jx B

Fig. 4.8. Net outward j × B force in a torus due to the poloidal ﬁeld.

| jx B

| > | jx B

××

Fig. 4.9. Net outward j × B force in a torus due to the toroidal ﬁeld.

92 Ideal magnetohydrodynamics

plasma plasma

perfectly conducting

wall

(a)

(b)

Fig. 4.10. A perfectly conducting wall can provide toroidal force balance for (a) poloidal

ﬁelds but not for (b) toroidal ﬁelds.

= µ

/2π R.TheR

−1

dependence means that B

is again stronger on the inner

side of the torus than on the outer side with the same result as before.

The net toroidal force is usually quite small compared with the forces involved in

radial pressure balance but the plasma and its self-generated ‘containing’ magnetic

ﬁeld cannot provide compensation which must, therefore, be applied externally.

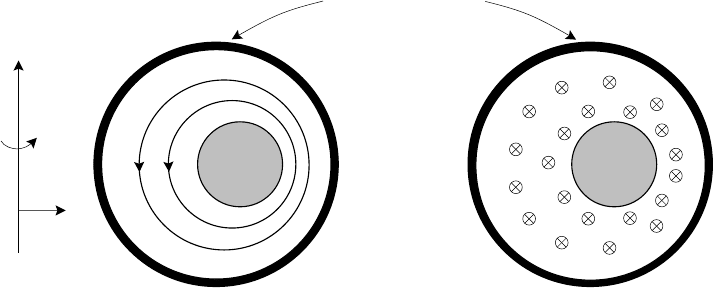
Provided there is a poloidal component of the magnetic ﬁeld outside the plasma, as

shown in Fig. 4.10(a), compensation may be provided by surrounding the plasma

with a perfectly conducting wall. Then, since ﬁeld lines cannot penetrate the wall

they are compressed as the plasma moves towards the wall and the increase in

magnetic pressure eventually balances the net toroidal force. Note that this does

not work if the external ﬁeld is purely toroidal since the ﬁeld lines are not trapped

between plasma and wall but can slip around the plasma as can be seen from Fig.

4.10(b). Since walls are not perfect conductors the compressed ﬁeld leaks away in

a ﬁnite time. This may be shorter than other times of interest which is a drawback

to this method.

Another approach is to impose a vertical magnetic ﬁeld by means of external

coils as shown in Fig. 4.11. By suitable choice of current direction the vertical ﬁeld

reinforces the poloidal ﬁeld on the outer side of the plasma and opposes it on the

inner side providing the desired compensation. Here again, note that this does not

work for a purely toroidal ﬁeld since the vertical ﬁeld is everywhere at right angles

to the toroidal ﬁeld and therefore has no effect. It follows that a poloidal component

of magnetic ﬁeld is essential for toroidal force balance.

4.3 Static equilibria 93

plasma

external coil

Fig. 4.11. Toroidal force balance provided by external coils.

φφ

∇B

E×B

Fig. 4.12. E × B drift due to toroidal ﬁeld.

Herein lies the dilemma of plasma containment. A theta-pinch has good radial

stability (the plasma sits in a magnetic well) but if bent into a torus, with no poloidal

ﬁeld, there is no toroidal equilibrium. On the other hand, a closed toroidal system

with a magnetic ﬁeld that is predominantly poloidal will have good toroidal equi-

librium but poor radial stability. The challenge is to ﬁnd the optimal mix of poloidal

and toroidal ﬁelds which can provide toroidal equilibrium without sacriﬁcing radial

stability.

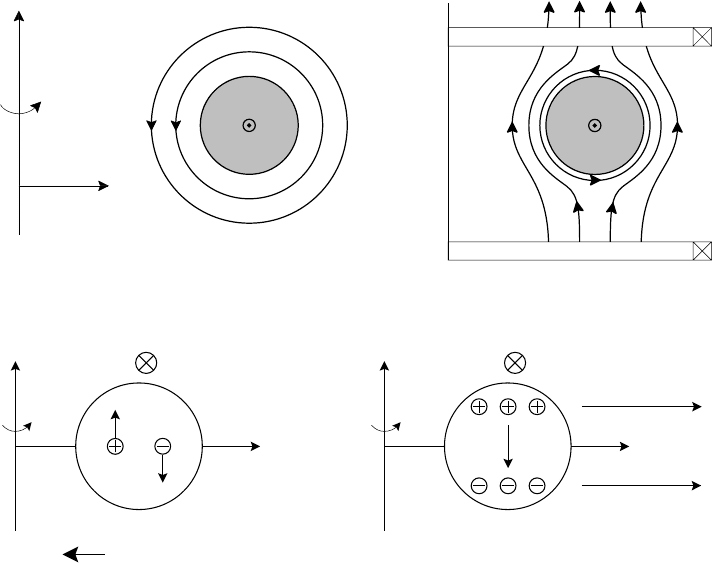
The problem of maintaining toroidal equilibrium can be described in terms of

particle orbits and was mentioned brieﬂy in Section 2.10. As noted there and above,

the toroidal ﬁeld generated by external coils decreases with major radius R across

the plasma. Consequently, there is a drift of the particle guiding centre relative to

the lines of force which is a combination of grad B and curvature drifts. Such drifts

are in opposite directions for ions and electrons so that an electric ﬁeld is created

and the E ×B drift (the same for both species) is radially outward as shown in Fig.

4.12. Thus, if there is only a toroidal ﬁeld there is no toroidal equilibrium.

94 Ideal magnetohydrodynamics

orbit

flux surfaces

2′

′

Fig. 4.13. Illustration of poloidal ﬁeld compensation for particle drift in a torus.

Now the introduction of a poloidal ﬁeld B

can compensate for the particle drift

as illustrated in Fig. 4.13. For simplicity, consider a ﬂux surface on which the

ﬁeld lines rotate once in the poloidal direction during one circuit in the toroidal

direction. With no drift a particle would simply gyrate about a ﬁeld line, which

for example starts at point 1 on the surface, reaches point 2 a quarter of the way

round, point 3 halfway round and so on, returning to point 1 after one toroidal

revolution. An upward drift (the case illustrated) causes the particle to leave this

particular ﬁeld line and move continuously across magnetic surfaces arriving at

points 2



and 3



instead of 2 and 3. Thereafter, an upward drift means that the

particle moves back towards the original magnetic surface arriving back at point 1

via point 4



The example we have considered is a particularly simple one. In general, neither

the particle nor the ﬁeld line will arrive back at the same point after one revolution

but will be displaced through some angle in the poloidal plane as illustrated in Fig.

4.14. In an equivalent cylinder of length 2π R

this angle is the rotational transform.

In a torus, in general, the change in poloidal angle per toroidal revolution depends

on the starting point, so the rotational transform is deﬁned as the average change

over a large number of revolutions

ι = lim

N →∞



n=1

θ

If ι is a rational fraction of 2π the line will eventually return to its starting position

(i.e. the ﬁeld lines are closed); if not, it is said to be ergodic.

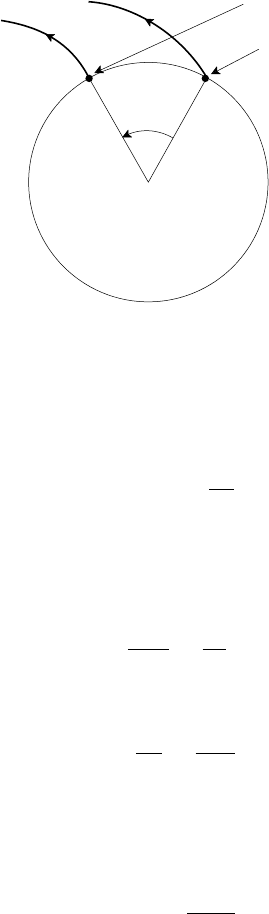
4.3 Static equilibria 95

returning point

starting point

∆

Fig. 4.14. Rotation of ﬁeld lines in a torus.

The safety factor q = 2π/ι and is therefore equal to the average number of

toroidal revolutions required to complete one poloidal revolution or

q = lim

N →∞

where N

, N

are the toroidal and poloidal winding numbers, respectively, and the

limit is taken over an inﬁnite number of revolutions. If φ is the average change

in toroidal angle for one poloidal revolution q = φ/2π and since

Rdφ

where ds is the distance moved in the poloidal plane, it follows that

q =

2π



ds (4.34)

where the integral is over a single poloidal circuit around the ﬂux surface. For a

torus of circular cross-section and large aspect ratio R

 a, where R

, a are the

major and minor axes, respectively, we may put R = R

and B

≈ B

) so that

q(r) =

(4.35)

in agreement with (4.29) for the cylindrical case.

Another representation for q can be obtained by considering the magnetic ﬂux

through an annulus between two neighbouring ﬂux surfaces, as illustrated in Fig.

4.15. The poloidal ﬂux through the annulus is

dψ = 2π RB

dx (4.36)

96 Ideal magnetohydrodynamics

toroidal flux

flux

poloidal

Fig. 4.15. Magnetic ﬂux through an annulus between ﬂux surfaces.

where dx is the separation at R between the ﬂux surfaces. The toroidal ﬂux is

d =



ds(B

dx) (4.37)

Substituting (4.36) in (4.34) and using (4.37) then gives

q =

d

dψ

expressing q as the rate of change of toroidal ﬂux with poloidal ﬂux.

To describe the equilibrium conﬁguration of a plasma torus we use the cylin-

drical coordinates (R,φ,Z) shown in Fig. 4.16(a) and assume toroidal axisym-

metry, i.e. there is no dependence on the azimuthal coordinate φ. It follows from

B = ∇ × A that we may write

=−

∂ψ

∂ Z

∂ψ

∂ R

(4.38)

where ψ = RA

is called the ﬂux function. We note that (B · ∇)ψ = 0, on

using (4.38), so that the magnetic surfaces are surfaces of constant ψ which may,

therefore, be used to label them. In fact, 2πψ is the total poloidal ﬂux through a

circle of radius R centred at the origin in the Z = 0 plane. Referring to Fig. 4.16(b)

we have



B · dS =



∇ × A · dS =



C(R)

A · dl = 2π RA

= 2πψ(R, 0)