Boyd T.J.M., Sanderson J.J. The Physics of Plasmas

Подождите немного. Документ загружается.

3.4 Applicability of the MHD equations 67

Combining this with (3.45) we have











1/2





 1 (3.58)

Apart from (3.47) to (3.49), which are fundamental to MHD and may therefore be

taken for granted, (3.58) summarizes the approximations of ideal MHD; the strong

inequalities involving (r

) represent the large scale length (high conductivity)

and small ion Larmor radius approximations, while the ﬁnal inequality represents

the high collisionality approximation. It is this last approximation that is least likely

to be valid for fusion and space plasmas which are usually better described as

collisionless rather than collision-dominated. Despite this, a ﬂuid description of

the plasma in these circumstances may still be tenable though some re-examination

of the model, particularly of the energy equation, is required. It turns out that the

magnetic ﬁeld, by acting as a localizing agent, is able to compensate in part for

insufﬁcient collisionality. However, discussion of this requires a proper recognition

of the anisotropic nature of a magnetized plasma.

3.4.1 Anisotropic plasmas

Since a magnetized plasma has a natural preferred direction the assumption of

isotropic pressure cannot strictly be justiﬁed. This point is relevant when the mag-

netic ﬁeld is sufﬁciently strong (or collisions sufﬁciently weak) so that

 λ

(3.59)

Consequently, in the plane perpendicular to the magnetic ﬁeld it is the Larmor

orbits rather than collisions that restrict the free ﬂow of the particles. It then may

happen that, instead of (3.11), the equilibrium stress tensor takes the form



 =−





⊥

0 P

⊥

00P







(3.60)

with different components parallel and perpendicular to the ﬁeld. In ideal MHD

one then obtains, instead of the adiabatic gas law (3.42), two separate adiabatic

conditions called the double adiabatic approximation.

We can see roughly how this comes about by returning to (3.24) and (3.26) and

splitting them into two pairs of equations for separate internal energy components

68 Macroscopic equations



and E

⊥

. Dropping all the dissipative terms and using (3.60) we write (3.24) as



=−



∂u

∂r

(3.61)

⊥

=−

⊥



∇ · u −

∂u

∂r



(3.62)

and from (3.26) we substitute

ρE



= P



/2 (3.63)

ρE

⊥

= P

⊥

(3.64)

An equation for ∂u

/∂r

is obtained from the parallel component of the magnetic

convection equation on expanding the right-hand side and using (2.5) to get

∂ B

∂t

+ (u · ∇)B = B

∂u

∂r

− B∇ · u (3.65)

Substituting for ∂u

/∂r

from (3.65) and, as before, for ∇ · u from the continuity

equation, it is easily veriﬁed that (3.61) and (3.62) become







= 0 (3.66)

and



⊥

ρ B



= 0 (3.67)

which are the double adiabatic conditions replacing (3.42) when the pressure is

anisotropic.

An interesting parallel may be drawn between the double adiabatic conditions

and the adiabatic invariants µ

and J of particle orbit theory. Since µ

= mv

⊥

/2B

and P

⊥

/ρ ∝v

⊥

/2, where the bracket denotes an average over all the particles

in the ﬂuid element, we may regard (3.67) as a macroscopic representation of the

invariance of µ

. Likewise, treating the ﬂuid element as a ﬂux tube and using

a well-known result of ideal MHD that the length of a ﬂux tube l ∝ B/ρ (see

Section 4.2), we have



∝v



l

∝ J

so that (3.66) becomes a statement of the invariance of J . These insights go some

way towards explaining why ideal MHD can be applied with success even in the

collisionless regime. However, they are not rigorous and uncritical use of MHD be-

yond the validity of its approximations can lead to erroneous results, as illustrated

by Kulsrud (1983).

3.4 Applicability of the MHD equations 69

The role of collisions in MHD is twofold; they not only establish the quasi-static

local equilibrium state but serve to deﬁne the dimensions of the ﬂuid element. In the

collisionless limit the adiabatic invariants describe the plasma locally and the ion

Larmor radius deﬁnes the perpendicular dimension of the ﬂuid element provided

(3.54) is valid, a condition well satisﬁed in almost all magnetized plasmas. The

outstanding problem is the deﬁnition of the parallel dimension of the ﬂuid element

since, in the collisionless limit, particles may ﬂow freely along the ﬁeld lines. In

particular, there must be negligible heat ﬂow from one ﬂuid element to another

and since the heat conduction coefﬁcient parallel to B increases with the collision

time a negligible parallel temperature gradient is required. This imposes a severe

restriction on the applicability of double adiabatic theory.

3.4.2 Collisionless MHD

One way to get around the problem of establishing a ﬂuid description for the par-

allel ﬂow in the collisionless limit is to use a one-dimensional kinetic equation to

describe v



-dependent plasma behaviour. This is done in the guiding centre plasma

model (Grad, 1967) but it is considerably more complicated than either ideal MHD

or double adiabatic theory and we shall not discuss it here.

With the objective of ﬁnding a simpler theory applicable to fusion plasmas,

Freidberg (1987) proposed an alternative ﬂuid model which he called collisionless

MHD. This model is worthy of consideration not only because it confronts the

problem that the strong collisions condition (3.45) is satisﬁed in neither fusion nor

space plasmas but also because it provides a link between the ﬂuid description

and particle orbit theory as developed in Chapter 2. Indeed, it is the relationship

between particle drifts and plasma currents that is the key to establishing the

collisionless MHD equations in the plane perpendicular to the magnetic ﬁeld.

The ﬁrst step is to write the velocity v of a particle as

v = v



b + v

⊥

+ v

where the perpendicular component has been separated into its rapidly changing

gyration around the ﬁeld line and its slowly changing guiding centre velocity. Next

we express v

in terms of all its possible components, evaluated in Chapter 2,

= v

+ v

where v

, v

and v

are given by (2.16), (2.22), (2.23) and (2.49), respectively.

We note that, in the MHD approximation (3.48), v

is of higher order than each

of the other terms and since it is the same for both ions and electrons and is

independent of v we see that to a ﬁrst approximation the plasma ﬂow velocity

70 Macroscopic equations

u = E × B/B

On taking the cross product of this equation with B we get

⊥

+ u × B = 0

the perpendicular component of Ohm’s law in ideal MHD.

Now, calculating the guiding centre current j

by summing over all the individual

particle contributions as in Chapter 2 we ﬁnd

b ×



⊥

∇B

+ P



(b · ∇)b) + ρ

⊥



where, as appropriate in a ﬂuid model, we have identiﬁed the partial pressures P

⊥

and P



with n

⊥

and 2n



, respectively. This correspondence has already been

noted in the preceding section.

To this guiding centre current we must add the magnetization current j

∇ × M, where M =−(P

⊥

/B)b so that the current density perpendicular to the

magnetic ﬁeld is

⊥

= j

+ j

The cross product of this equation with B then gives the perpendicular momentum

equation



b ×

⊥



× b = j × B − ∇

⊥

− (P



− P

⊥

)(b · ∇)b (3.68)

This is the perpendicular momentum equation found from both the guiding cen-

tre plasma model and the double adiabatic theory of Chew, Goldberger and Low

(1956).

Freidberg replaced the parallel momentum equation by the heuristic assumption

of incompressibility, ∇ · u = 0, which implies that the density and pressures are

convected with the plasma. The main role of the ‘parallel’ equations is to describe

the propagation of sound waves along the ﬁeld lines. But these waves do not couple

strongly with most ideal MHD instabilities which involve incompressible wave

motion. Thus, as Freidberg points out, for the most part the model is inaccurate

only where it does not matter and collisionless MHD should at least provide a

credible basis for the discussion of ideal MHD stability. If it is assumed that P

⊥



then the equations and predictions of collisionless MHD and incompressible,

ideal MHD are virtually identical. Furthermore, in those situations where the two

models produce different predictions, neither model can be considered reliable. The

evolution equations and conditions governing collisionless MHD for P

⊥

= P



= P

are set out in Table 3.3.

3.5 Plasma wave equations 71

Table 3.3. Collisionless MHD equations

Evolution equations:

Dρ/Dt = 0

ρ(Du

⊥

/Dt)

⊥

= (∇ × B) × B/µ

− ∇

⊥

DP/Dt = 0

∂B/∂t = ∇ × (u × B)

Equations of constraint:

∇ · B = 0 ∇ · u = 0

Deﬁnitions:

E =−u × B

j = (∇ × B)/µ

q =−ε

∇ · (u × B)

Approximations:

Collisionless: τ

 τ

 λ

Non-relativistic: ω/k ∼ L

/τ

∼ u  c

Quasi-neutrality: ω|

|/ω

 1

Small Larmor radius: r

 β

1/2

3.5 Plasma wave equations

The interaction of plasma and electromagnetic ﬁelds generates a very wide spec-

trum of wave phenomena of which only the low frequency limit is described by

MHD. A ﬂuid description of plasma wave propagation is feasible but cannot be

derived from a collision-dominated model since most wave frequencies are greater

than collision frequencies. Also, such a description must be two-ﬂuid since much

of the physics is related to the differences in ion and electron motion.

Neighbouring particles of a given species will tend to move coherently in re-

sponse to the ﬁelds but disperse on account of their random, thermal velocities.

The persistence of a ﬂuid element depends, therefore, on the dominance of the ﬁrst

effect over the second and we can express this in terms of a strong inequality by

requiring the distance moved by a particle on account of its thermal speed V

one wave period to be much less than the wavelength of the ﬁeld ﬂuctuations

2π

 λ



= v

(3.69)

72 Macroscopic equations

Table 3.4. Cold plasma wave equations

Wave equations:

∂n

/∂t + ∇ · (n

) = 0

(∂/∂t + u

· ∇)u

= e

(E + u

× B)

Maxwell equations:

∇ × E =−∂B/∂t

∇ × B = ε

∂E/∂t + µ

∇ · E = q/ε

∇ · B = 0

Approximations:

Cold plasma: V

 ω/k = v

Collisionless: ν

 ω

where v

is the phase velocity of the wave. This is the cold plasma approximation

and in the limit V

→ 0 the ﬂuid description is exact for a collisionless plasma

since, at any given point in the plasma, the velocity of all the particles of a given

species is uniquely determined by the species ﬂow velocity u

and the forces acting

on the particles are given by the ﬁelds at that point. Thus, the cold plasma wave

equations are simply the (separate) ion and electron continuity equations and equa-

tions of motion. In the latter the electric ﬁeld is retained because the non-relativistic

approximation (v

 c) is not assumed and the ﬁelds E and B are determined by

the full Maxwell equations, i.e. the displacement current is retained. The equations

are listed in Table 3.4.

The cold plasma wave equations provide a very good description of wave

phenomena in collisionless plasmas, especially at the high frequency end of the

spectrum. However, they inevitably become invalid at wave resonances where

k →∞. The effects of ﬁnite temperature may be investigated by introducing

pressure gradients into the equations of motion and adding the adiabatic equations

of state to determine the isotropic (or anisotropic) pressures. These are the warm

plasma wave equations which, for the case of isotropic pressures, are listed in

Table 3.5. In the adiabatic equations ρ

= m

and we have allowed for distinct

ratios of the speciﬁc heats. The warm plasma wave equations are model equations

for they have no rigorous derivation and, as discussed later, the ﬂuid model omits

important kinetic effects like Landau damping. Nevertheless, they provide a simple

description of ﬁnite temperature modiﬁcations of cold plasma waves and of the

further ﬂuid modes which propagate in a warm plasma but disappear in the cold

plasma limit.

3.5 Plasma wave equations 73

Table 3.5. Warm plasma wave equations

Wave equations:

∂n

/∂t + ∇ · (n

) = 0

(∂/∂t + u

· ∇)u

= e

(E + u

× B) − ∇ p

D( p

−γ

)/Dt = 0

Maxwell equations:

∇ × E =−∂B/∂t

∇ × B = ε

∂E/∂t + µ

∇ · E = q/ε

∇ · B = 0

Collisionless approximation: ν

 ω

3.5.1 Generalized Ohm’s law

For warm plasma waves it is sometimes necessary to include in the equations of

motion a term to represent the exchange of momentum between species. As in

Section 3.4 (see (3.51)), we write the rate of ﬂow of momentum from electrons to

ions as m

− u

). Using the approximations (3.50) and ignoring quadratic

terms (u

· ∇)u

it is then straightforward (see Exercise 3.6) to combine the

equations of motion to obtain a generalized Ohm’s law in the form

E + u × B − j/σ −

σν

∂j

∂t

Zeρ

(

j × B − ∇ p

)

(3.70)

This differs from (3.52) through the additional ∂j/∂t term which is negligible in

the MHD approximation because j is assumed to vary on the hydrodynamic time

scale and ν

 1. In the warm plasma wave equations, j and u

may vary

on a collision time scale and it is easily veriﬁed that inserting the inertial term

∂u

/∂t in (3.51) and using (3.50) yields (3.70).

Neither derivation of the generalized Ohm’s law presented in this chapter is

mathematically rigorous. However, as discussed in Section 12.6.2, Balescu (1988)

has shown that in the MHD approximation the effect of the inertial terms is tran-

sient and dies out after a few collision times so that the MHD version of the

generalized Ohm’s law (3.52) can be rigorously derived. On the other hand, there

is no rigorous derivation of (3.70) and this form of the generalized Ohm’s law, like

the warm plasma wave equations and the scalar Ohm’s law (3.35), has the status of

a model equation.

74 Macroscopic equations

3.6 Boundary conditions

In problems where the plasma may be treated as inﬁnite the boundary conditions

take the simple form of prescribed values at inﬁnity and perhaps at certain internal

points. More realistically, they are conditions to be satisﬁed by the solutions ob-

tained in different regions on the boundary between them. Typically, a plasma may

be surrounded by a vacuum and the boundary conditions, applied at the plasma–

vacuum interface, relate the solution of the ﬂuid and ﬁeld equations in the plasma

to the solution of the ﬁeld equations in the vacuum; the vacuum may extend to

inﬁnity or be surrounded by a wall and further appropriate boundary conditions are

applied to the vacuum ﬁelds.

Although in reality all variables change continuously across boundaries they of-

ten do so very rapidly and it is convenient to treat the boundary as an inﬁnitesimally

thin surface across which discontinuous changes take place. Differential equations

become invalid when the variables or their derivatives are discontinuous but by

integrating the equations over an inﬁnitesimal volume or surface which straddles

the boundary we derive conditions which relate the values of the variables on either

side of the boundary in terms of some surface quantity. The electromagnetic bound-

ary conditions are a familiar example of this procedure. Provided that there are

only volume distributions of current and charge the ﬁeld variables are continuous

across the boundary between two media. However, if either medium is a conduc-

tor containing a surface current or charge, then the tangential component of the

magnetic ﬁeld and the normal component of the electric ﬁeld suffer discontinuities

determined by the surface current and charge respectively.

In ideal MHD there is no space charge and therefore no surface charge. On the

other hand, the thickness of the skin current in a good conductor decreases as the

conductivity increases and, in the ideal MHD limit, such currents become surface

currents ﬂowing in a skin of inﬁnitesimal thickness. Here, since E is determined by

Ohm’s law, we are concerned with the boundary conditions on B. As in electromag-

netism these are obtained by integrating ∇ ·B = 0 and Amp

ere’s law over a small

cylindrical volume and rectangular surface, respectively, leading to the well-known

results (see Fig. 3.3 and Exercise 3.7)

[n · B]

= 0 (3.71)

[n × B]

= µ

(3.72)

where n is the unit vector normal to the boundary surface from side 1 to side 2,

[X ]

= X

−X

is the change in X across the surface, and J

is the surface current.

Another important boundary condition at a plasma–vacuum surface in ideal

MHD is obtained by applying the same procedure used to obtain (3.71) to the

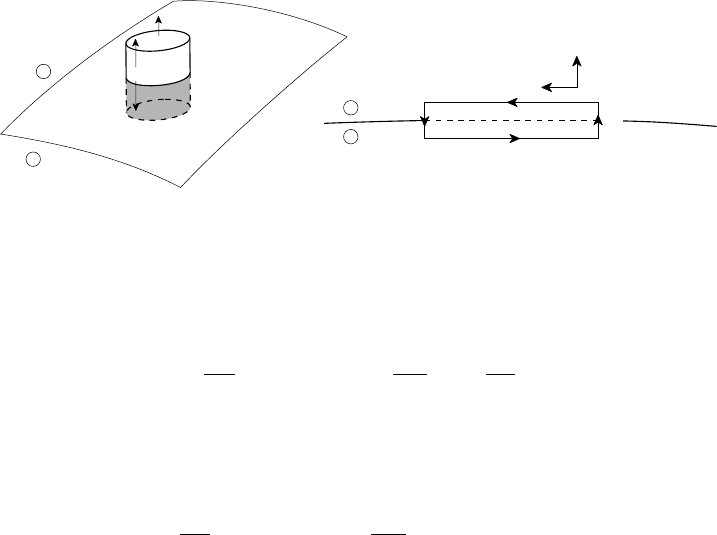
3.6 Boundary conditions 75

δl

δh

(b)

(a)

Fig. 3.3. Boundary volume and surface integrals.

momentum equation. In the next chapter we show that this equation may be written

=−∇ ·



P +

2µ



I −



where I is the unit dyadic. Integrating this equation over the volume of the inﬁnites-

imal cylinder whose ends are either side of the boundary surface as shown in Fig.

3.3(a) and using Gauss’ theorem gives



dV =





P +

2µ



n − (B · n)B



where V is the volume of the cylinder and S is its surface. As the length, l,ofthe

cylinder tends to zero the contribution to the surface integral from the curved sur-

face vanishes leaving only the normal contribution from either side of the boundary.

Further, since the plasma is a perfect conductor, there is no normal component of B

at the surface and so the second term in the square bracket also vanishes as l → 0.

Finally, since the acceleration of the plasma must remain ﬁnite, the volume integral

vanishes as l, and hence V , tends to zero. Thus,

[P + B

/2µ

]

= 0 (3.73)

i.e. the total pressure (plasma plus magnetic) is continuous at the boundary. Of

course, if the plasma density ρ → 0 at the boundary then P → 0 and (3.73)

requires that the magnetic pressure be continuous. Since in this case there can be no

surface current, this is consistent with (3.71) and (3.72) expressing the continuity

of both normal and tangential components of B.

The vanishing of the normal component of B at the surface of a perfect conductor

also means that in ideal MHD, at a plasma–vacuum interface, (3.71) is replaced by

the stronger conditions

B · n = 0 =

B · n (3.74)

where B and

B are the plasma and vacuum ﬁelds, respectively.

76 Macroscopic equations

Exercises

3.1 In general the motion of a plasma is determined by the action of both

applied and induced ﬁelds. Under what circumstances is it necessary to

investigate plasma dynamics using ﬂuid equations rather than particle orbit

theory?

What are the main features distinguishing the MHD and plasma wave

descriptions?

What is the essential difference between the hot and cold plasma wave

equations? State this in terms of a strong inequality.

3.2 What are the essential properties of a plasma ﬂuid element and how may

they be expressed in terms of dimensionless parameters?

Why do short range inter-particle forces produce a net change in the

momentum of a ﬂuid element only at its surface?

3.3 What is the assumption that allows us to use the thermodynamic equations

of state in MHD? Express this in terms of a strong inequality.

The ﬁrst law of thermodynamics (3.17) relates the change in internal

energy of a plasma to the work done and heat exchange in effecting the

transition from one equilibrium state of the plasma to another. What is the

fundamental distinction between the state variable E and the path variables

W and Q? What deﬁnes an adiabatic change of state?

3.4 Carry out the steps indicated in the text to obtain (3.27) describing the

evolution of the plasma pressure. What is the physical signiﬁcance of each

of the terms on the right-hand side of this equation?

3.5 By a dimensional analysis of the Maxwell equations, show that the dis-

placement current and the electrostatic force may be neglected in the non-

relativistic approximation. What does this mean physically in terms of the

reaction of the plasma to the electrostatic ﬁeld compared with its reaction

to the electromagnetic ﬁelds in MHD?

Verify your answer by showing, from the equation of charge conserva-

tion and j = σ E, that any net space charge will decay away in a time of

order ε

/σ .

Why, in general, is the non-relativistic approximation not adequate in

plasma wave theory?

3.6 Obtain (3.70) by combining the ion and electron equations of motion.

Show, also, that it may be derived by retaining the neglected electron

inertial term m

∂u

/∂t in (3.51) and substituting for u

and u

from

(3.50).

3.7 By integrating ∇ · B = 0 and Amp

ere’s law across the boundaries illus-

trated in Fig. 3.3 derive the boundary conditions (3.71) and (3.72).