Boyd T.J.M., Sanderson J.J. The Physics of Plasmas

Подождите немного. Документ загружается.

4.3 Static equilibria 97

plan view

(z = 0)

(a)

(b)

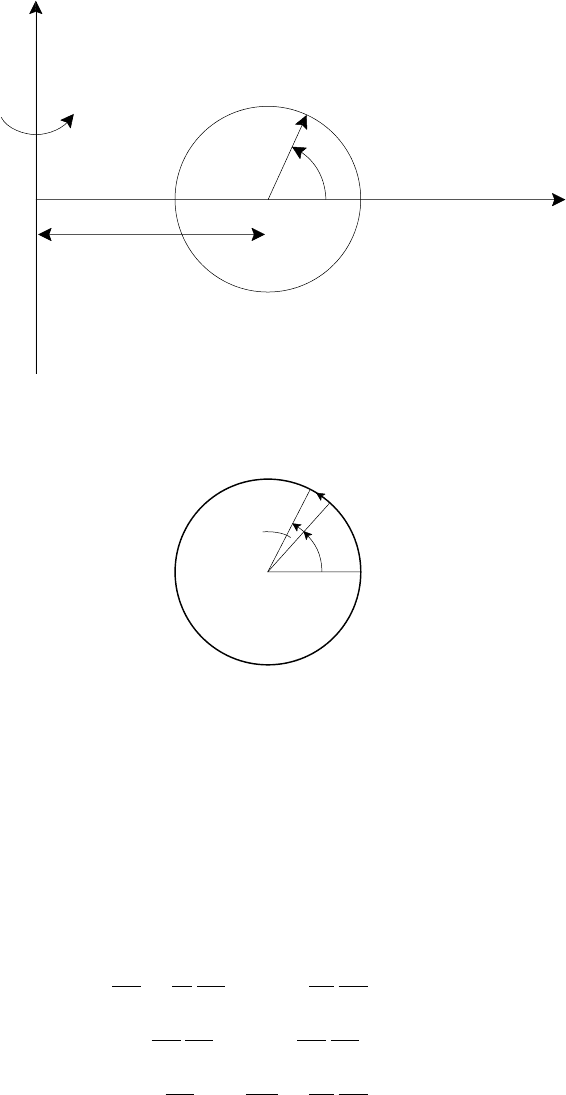
Fig. 4.16. Coordinate conﬁguration of a torus in (a) side and (b) plan view.

where we have used Stokes’ theorem to convert the surface integral to a line

integral. Now substituting (4.12) in (4.10) and using (4.38) for B

and B

get

∂ P

∂ R

∂

∂ R

(RB

) +

∂ψ

∂ R



∗

ψ = 0 (4.39)

∂ψ

∂ R

∂

∂ Z

(RB

) −

∂ψ

∂ Z

∂

∂ R

(RB

) = 0 (4.40)

∂ P

∂ Z

+ B

∂ B

∂ Z

∂ψ

∂ Z



∗

ψ = 0 (4.41)

98 Ideal magnetohydrodynamics

where



∗

ψ =

∂

∂ R

−

∂ψ

∂ R

∂

∂ Z

(4.42)

and we have identiﬁed B

as the toroidal magnetic ﬁeld B

Equation (4.40) may be written as ∇ψ ×∇(RB

) = 0 showing that surfaces of

constant RB

are also surfaces of constant ψ, i.e. RB

= F(ψ), for some function

F. In fact, F(ψ) is related to the total poloidal current I

through the disc of radius

R shown in Fig. 4.16(b). We have



j · dS =



∇ × B · dS =



C(R)

B · dl =

2π RB

(4.43)

Thus, F(ψ) = µ

(ψ)/2π. Substituting this result in (4.39) and (4.41), multiply-

ing by ∂ψ/∂Z and ∂ψ/∂R respectively, and subtracting gives

∂ P

∂ R

∂ψ

∂ Z

−

∂ P

∂ Z

∂ψ

∂ R

= 0

i.e. ∇P ×∇ψ = 0. Hence P = P(ψ), a result we already know since the magnetic

surfaces are isobaric surfaces.

Finally, since P and RB

are functions of ψ we may write (4.39) as



∗

ψ + FF



+ µ



= 0 (4.44)

where the prime denotes differentiation with respect to ψ. This is the general

equation for axisymmetric, toroidal equilibria and is known as the Grad–Shafranov

equation. It is a non-linear partial differential equation, derived from the ideal

MHD equations for static, toroidal equilibria with azimuthal symmetry (∂/∂φ ≡

0), for the ﬂux function ψ which determines the poloidal magnetic ﬁeld. It ex-

presses the balance between plasma pressure gradient (third term) and the j × B

contributions (ﬁrst and second terms). Of the latter, the ﬁrst term represents the

toroidal current and poloidal ﬁeld, which we identiﬁed as essential for toroidal

stability, and the second term comes from the poloidal current and toroidal ﬁeld

determining radial stability. Indeed, it is easy to see that if we drop the ﬁrst term in

(4.44) we can integrate and by using (4.43) recover (4.19), the equation for radial

equilibrium in a theta-pinch.

Solutions to the Grad–Shafranov equation provide a complete characterization

of axisymmetric ideal MHD equilibria. The nature of the equilibrium conﬁguration

is determined by the choice of the two arbitrary functions P(ψ) and F(ψ),for

the pressure and current proﬁles, together with the boundary conditions. Given

P and F , (4.44) is solved as a boundary value problem to ﬁnd the ﬂux function

ψ(R, Z). The main difﬁculty lies in the fact that P and F are themselves func-

tions of ψ , which is not known until (4.44) is solved. Although some progress

4.3 Static equilibria 99

~ 1

RRR

βββ

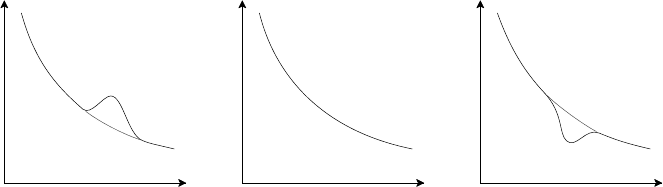
Fig. 4.17. Toroidal ﬁeld variation with major radius in a tokamak.

can be made analytically either in closed form under certain restrictive conditions

(see Exercise 4.4) or by expansion in terms of the inverse aspect ratio, a/R

the Grad–Shafranov equation generally has to be solved numerically (see Sec-

tion 4.3.3).

Before discussing numerical solutions it is instructive to consider brieﬂy three

limiting cases within the general equation. By setting FF



(ψ) = 0 we discard

the poloidal current in the plasma. The toroidal magnetic ﬁeld behaves as R

−1

and pressure balance is maintained solely by j

× B

. For this case β

= 1. On

the other hand, P



(ψ) = 0 corresponds to the special case in which the magnetic

ﬁeld is force-free, in the sense to be described in Section 4.3.4, and there is no

containment. When pressure balance is maintained predominantly by j

× B

, the

poloidal current term in the Grad–Shafranov equation FF



(ψ) |

∗

ψ| and the

conﬁguration is characterized by β

 1 (high beta tokamak). The behaviour of B

as a function of the major radius of the tokamak is shown in Fig. 4.17 for different

magnitudes of β

Three examples of toroidal conﬁgurations are illustrated in Fig. 4.18. Since the

compensating force required for toroidal equilibrium is usually much smaller than

those involved in radial force balance one would expect |B

||B

| as in the

tokamak and screw pinch. In fact, for tokamaks |B

| > |B

/a which means that

a ﬁeld line makes several transits around the torus before completing one spiral of

the minor axis. The toroidal current ﬂows mainly in the plasma column.

In the screw pinch, on the other hand, the current ﬂows mainly in a sheath

surrounding the plasma column. Likewise, the poloidal ﬁeld does not penetrate

the plasma and in the vacuum |B

|∼|B

/a.

The reversed ﬁeld pinch differs in that |B

|∼|B

| so that the ﬁeld lines spiral

many times around the magnetic axis in going once round the torus. One would

not expect containment from such a high poloidal ﬁeld because the associated

large toroidal current is inimical to radial stability. However, as we shall discuss in

Section 4.7.1, strong magnetic shear can act as a stabilizing mechanism to provide

100 Ideal magnetohydrodynamics

(a)

)

(b)

Fig. 4.18. Toroidal and poloidal ﬁelds in (a) tokamak, (b) screw pinch, (c) reversed ﬁeld

pinch.

a stable conﬁguration in which the toroidal ﬁeld reverses its direction in the outer

part of the plasma column, known as the reversed ﬁeld pinch.

4.3.3 Numerical solution of the Grad–Shafranov equation

Structurally, the Grad–Shafranov equation in the form 

∗

ψ = S(r,ψ), where S is

a non-linear functional of ψ, is a second-order, non-linear elliptic partial differen-

tial equation. Apart from a number of special cases, two-dimensional axisymmetric

equilibria have to be determined numerically. Equilibria are determined by the

choice of S(r,ψ), i.e. P(ψ) and F(ψ), along with speciﬁed boundary conditions.

In the simplest case the plasma might be contained within a conducting shell at

which ψ is speciﬁed; this corresponds to a ﬁxed-boundary problem. If, on the other

hand, a region of vacuum is present between the plasma and the conducting shell

we have a free–boundary problem since neither the position nor the shape of the

boundary are known. In practice both the position and shape of the plasma are

determined by external coils carrying known currents. Alternatively, the inverse

problem prescribes the boundary and then leaves the current distributions needed

to provide this to be determined. Codes are used to solve the Grad–Shafranov

equation for tokamak equilibria. Here we limit ourselves to solving a simple model

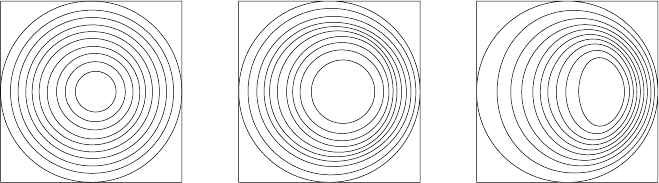
4.3 Static equilibria 101

(a) (b) (c)

Fig. 4.19. Flux surfaces for tokamak equilibria for (a) β

< 1, (b) β

∼ 1, (c) β

> 1.

problem of a plasma bounded by a perfectly conducting boundary with circular

cross-section. By and large, techniques for solving elliptic equations use direct or

iterative methods. The matrix equation resulting from a ﬁnite difference discretiza-

tion in the (R, Z) plane, though large, is sparse and is readily solved iteratively

(Press et al. (1989)).

To characterize particular tokamak equilibria means prescribing functional

forms for P(ψ) and F(ψ). Sections of a cosine function were used to compute

the ﬂux surfaces shown in Fig. 4.19 for values of β

corresponding to A

−1

, A

and A where A is the aspect ratio R

/a.Forβ

∼ A

−1

the current and magnetic

ﬁeld are approximately collinear so that the entire plasma is very nearly force-free.

The poloidal current j

∼ (B

) j

gives rise to an enhancement of B

; FF



< 0

and the ﬂux surfaces for this case are approximately concentric circles. At a later

stage of the discharge the rise in plasma pressure means that β

∼ 1 and a dia-

magnetic current now tends to annul the poloidal current with the result that the

magnetic surfaces are displaced toward the outer wall of the tokamak as shown in

Fig. 4.19(b).

Increasing β

to values of the order of A and above results in ﬂux surfaces that

are displaced yet further outwards. This shift is known as the Shafranov shift. Flux

surfaces are now compressed on the outside with a corresponding expansion on

the inside. To obtain high-beta equilibria FF



must be large and positive. The

poloidal current is reversed from the β

< 1 case and is comparable in magnitude

to the toroidal current. The B

proﬁle (Fig. 4.17) shows that a diamagnetic well

is now created and this feature is largely responsible for radial pressure balance.

While radial pressure balance for high-beta tokamaks is achieved largely by the

poloidal diamagnetic currents induced in the plasma (as in a theta-pinch), the

toroidal current provides toroidal force balance but is limited on account of the

stability requirement q ≥ 1 (see Section 4.5).

102 Ideal magnetohydrodynamics

πR

Fig. 4.20. Cylindrical ﬂux tube with uniform twist.

4.3.4 Force-free ﬁelds and magnetic helicity

Although in the outer regions of stars both gas pressure and gravity may be negli-

gible, the plasma can carry signiﬁcant currents. If there is to be equilibrium in such

regions it follows that the Lorentz force j × B must vanish also, i.e. the ﬁeld must

be force-free. This means that j and B are parallel so that we may write

∇ × B = αB (4.45)

where, in general, α will be spatially dependent. However, taking the divergence

of (4.45) and using ∇ · B = 0, we see that α must obey

B · ∇α = 0

i.e. α is constant along a ﬁeld line. The implication of (4.45) is that as one follows

a particular ﬁeld line the neighbouring ﬁeld lines rotate in a constant manner about

it.

A simple example of a force-free ﬁeld can be obtained by starting with a cylindri-

cal ﬂux tube in which the ﬁeld lines are initially all parallel to the axis, B = B

(r)

and rotating one end of it through an angle ι = 2π R

, keeping the other end ﬁxed,

as shown in Fig. 4.20. Note that ι is the same for all r so that everywhere

(r)

= r

dθ

rι

2π R

= r (4.46)

4.3 Static equilibria 103

where  is the uniform twist (rotation per unit length) of the ﬁeld. Putting P = 0

in (4.18) and substituting for B

(r) from (4.46) gives

2

1 + 

= 0

which integrates to yield the result

(r) =

1 + 

(r) =

rB

1 + 

where B

is the value of B

on the axis. It is easily veriﬁed from (4.45) that α(r) =

2/(1 +

) in this example.

An important theorem about force-free ﬁelds is that an isolated conducting ﬂuid

mass cannot have a ﬁeld that is force-free everywhere. This follows from the virial

theorem (see p. 84) on putting ∇ P = 0 and means that a force-free ﬁeld must

be anchored on a bounding surface; it cannot arise entirely from currents within a

ﬁnite volume.

Further theorems relating to force-free ﬁelds in closed systems were proved by

Woltjer (1958). He showed the invariance of the quantity

K =



A · B dτ

where A is the vector potential (B = ∇×A) with the integral taken over the whole

volume of the closed system, and then used this to prove that force-free ﬁelds with

constant α represent the state of minimum energy in a closed system. K , known

as the magnetic helicity, provides a measure of the complexity of the magnetic

ﬁeld topology since it represents the interlinking of magnetic ﬁeld lines. In ideal

MHD a closed ﬁeld line interlinking another with given connectivity maintains this

connectivity through any plasma motion with the consequence that the topological

properties of the ﬁeld are preserved.

To establish the invariance of K we use (3.5) to get



A ·

∂B

∂t

dτ +



∂A

∂t

· B dτ

Then substituting B = ∇ × A and using the expansion of ∇ · (∂A/∂t × A) we

obtain





∇ ·



∂A

∂t

× A



+ 2

∂A

∂t

· ∇ × A



dτ

From (4.4) we have

∂A

∂t

= u × ∇ × A

104 Ideal magnetohydrodynamics

so the second term in the integral vanishes. Using Gauss’ theorem the ﬁrst term

may be converted to the integral of (∂A/∂t × A) over the surface of the closed

system. However, ∂A/∂t must vanish on this surface since A is continuous across

the surface and the motions inside a closed system cannot affect the vector potential

outside the system. This establishes the invariance of K .

Next we examine the stationary values of the magnetic energy



/2µ

)dτ

subject to the condition that K is constant, i.e. we take the variation of W

−

K ,

obtaining



−







B · δB −

(δA · B + A · δB)



dτ

Substituting δB = ∇ × δA and again using the expansion of the divergence of a

vector product this becomes



−







∇ ·



δA × B +

A × δA



+ (∇ × B − α

B) · δA



dτ



(∇ × B − α

B) · δA dτ

on using Gauss’ theorem to convert the ﬁrst term to a surface integral which again

vanishes since δA is zero on the boundary. Thus, for arbitrary choice of δA there is

an extremum if and only if

∇ × B = α

B (4.47)

in which α

is a constant.

Because of their importance in astrophysics much effort has been put into ﬁnding

such ﬁelds. Taking the curl of (4.47) gives the Helmholtz equation

(∇

+ α

)B = 0 (4.48)

the solutions of which are well-known. However, it must be remembered that this

increases the differential order of the equation and not all solutions of (4.48) satisfy

(4.47).

Another approach to the investigation of force-free ﬁelds uses the Clebsch vari-

able representation

B = ∇α × ∇β (4.49)

4.4 Solar MHD equilibria 105

introduced in Section 2.9. It is clear from this representation that (4.49) satisﬁes

∇ · B = 0. Also, since

B · ∇α = 0 = B ·∇β (4.50)

it follows that α and β are constant on each ﬁeld line and, therefore, may be used

to label each ﬁeld line. Substitution of (4.45) in (4.50) and using (4.49) for B gives

[∇ × (∇α × ∇β)] · ∇α = 0 = [∇ × (∇α × ∇β)] · ∇β (4.51)

as coupled differential equations to be solved for α and β.

Only a limited range of solutions of such non-linear equations may be found

by analytical methods. However, numerical solutions may be generated using

variational techniques. This is discussed in Sturrock (1994) in which the Clebsch

variable representation is used to show that δW = 0 leads to force-free ﬁeld conﬁg-

urations, provided α and β are constant on the bounding surface (see Exercise 4.5).

4.4 Solar MHD equilibria

Magnetic ﬁelds play a key role in solar physics ranging from their creation through

dynamo action to their role in sunspot formation and in dramatic, if transient,

phenomena such as solar ﬂares. As a consequence, many aspects of solar physics

are governed by magnetohydrodynamics. The plasma beta serves as an index of the

relative importance of magnetic effects. In this section we make use of a simple ﬂux

tube model, developed by Parker (1955), to gain insights into aspects of solar MHD

equilibria. Parker’s ﬂux tube model is particularly useful in view of the subsequent

realization that virtually all the magnetic ﬂux extruding from the surface of the Sun

is concentrated into isolated ﬂux tubes or bundles of these.

The long-held view that the background magnetic ﬁeld at the Sun’s surface was

weak was undermined by high resolution observations that uncovered a hierarchy

of magnetic structures. While the mean ﬁeld over large regions of the surface of the

Sun is indeed no more than ∼0.5 mT, these observations showed that the magnetic

ﬂux through the surface, far from being uniform, is concentrated into ﬂux tubes

with intensities typically a few hundred times the mean ﬁeld, over diameters of a

few hundred kilometres. This localization of ﬂux is not what one might expect

intuitively. The region across which the ﬂux tube bursts through the surface is

known as a magnetic knot and was ﬁrst identiﬁed by Beckers and Schr

oter (1968)

from high resolution H

pictures. They estimated that around 90% of the ﬂux in

active regions is accounted for by ﬂux tubes appearing at magnetic knots. Beyond

the appearance of knots the picture is yet more complicated, with knots attracting

one another to form aggregates of ﬂux tubes which in turn break up or, more

rarely, go on to develop into sunspots, extending across regions with scale lengths

106 Ideal magnetohydrodynamics

typically hundreds of times that of a magnetic knot. These observations led to a

reappraisal of the solar magnetic ﬁeld. The picture now appears to be one in which

magnetic ﬂux penetrating the surface of the Sun is concentrated into intense ﬂux

tubes distributed over the surface.

Of the many questions raised by these observations perhaps the most puzzling

is why the Sun’s magnetic ﬁeld should appear as intense isolated ﬂux tubes sur-

rounded by ﬁeld-free zones, a conﬁguration that is to say the least counter-intuitive.

Conventionally one might picture the magnetic ﬁeld spreading to ﬁll the whole

of space allowed by the tension B

/µ

along the lines of force. However Parker

(1955) pointed out that allowing for the solar gravitational ﬁeld results in magnetic

buoyancy and this buoyancy is responsible for isolating the magnetic ﬁeld into

individual ﬂux tubes.

4.4.1 Magnetic buoyancy

Consider the magnetohydrostatic equilibrium of a ﬂux tube deep in the photosphere

(see Fig. 4.21). Following Parker, we assume that the ﬂux tube is slender, in the

sense that its diameter is small compared with scale lengths characterizing varia-

tions along the tube, as for example the radius of curvature. Allowing for the Sun’s

gravitational ﬁeld, the magnetohydrostatic condition is now expressed as

(∇ × B) × B − ∇ P − ρ∇ψ = 0 (4.52)

where ψ is the gravitational potential. For simplicity we assume that initially the

ﬂux tube is horizontal and aligned in the x-direction. The ﬂuid pressure within the

ﬂux tube, P

int

(x, z), is governed by a purely hydrostatic equilibrium. If we neglect

the ﬁeld from any neighbouring ﬂux tubes pressure balance across the ﬂux tube is

simply expressed by equating the external pressure P

ext

to the total internal pressure

ext

(x, z) = P

int

(x, z) +

(x, z)

2µ

(4.53)

Thus the ﬁeld strength is determined by the ambient ﬂuid pressure which in turn is

a function of the gravitational potential ψ, so that B = B(ψ). Assuming the ﬂuid

is governed by the equation of state for an ideal gas P = ρk

T/m, where ρ is the

mass density and m the particle mass, and the temperature is uniform, the external

density ρ

must exceed the internal density ρ

. There is, therefore, a buoyancy force

A(ρ

− ρ

)∇ψ per unit length where A denotes the cross-section of the ﬂux tube.

The magnitude of this force F per unit length is then

F =

2µ



(4.54)