Boyd T.J.M., Sanderson J.J. The Physics of Plasmas
Подождите немного. Документ загружается.

6.4 Waves in warm plasmas 227
limits as α
2
< 1, β
2
e
< 1, α
2
+ β
2
e
> 1, we see that this is region 5 and putting
ω = (1 − )(ω
2
p
+
2
e
sin
2
θ)
1/2
, where again 0 < 1, we find
ω ≈ (ω
2
p
+
2
e
sin
2
θ)
1/2
[1 − ω
2
p
2
e
sin
2
θ/2k
2
c
2
(ω
2
p
+
2
e
sin
2
θ)]
for the dispersion relation near the resonance.
6.4 Waves in warm plasmas
Cold plasma theory has shown clearly the existence of a large number of waves in
an anisotropic, loss-free plasma. The theory is valid provided the plasma is cold, i.e.
the thermal velocity is much smaller than v
p
. This approximation obviously breaks
down near a resonance where the phase velocity v
p
→ 0. We shall now consider
some finite temperature modifications of the theory, still within the confines of a
fluid description. This we may do by adding pressure terms to the fluid equations
although we underline a fundamental difference between cold and warm plasma
theory. Whereas cold plasma theory is properly a fluid theory, to describe warm
plasma behaviour fully we need to make use of kinetic theory. In part this is because
pressure is due to particle collisions which may lead to wave damping. However,
even in a dissipation-free plasma the fluid equations give an incomplete picture of
warm plasma wave motion.
A prime example of the shortcomings of the fluid approach appears in the
description of electron plasma waves. In the cold plasma limit, these are simply
oscillations at ω = ω
p
, i.e. they do not propagate. In a finite temperature plasma,
on the other hand, the dispersion relation is ω
2
= ω
2
p
+ k
2
V
2
where the thermal
velocity V is given by
V
2
= (γ
i
k
B
T
i0
/m
i
+ γ
e
k
B
T
e0
/m
e
) (6.84)
Moreover, this result is obtained (for sufficiently small k) regardless of whether we
use the fluid equations or kinetic theory. However, from a kinetic theory treatment,
additional information is retrieved that is lost in fluid theory; in particular, we find
that electron plasma waves in an equilibrium plasma are damped even though inter-
particle collisions are negligible. This phenomenon, known as Landau damping,
comes about because those electrons which have thermal velocities approximately
equal to the wave phase velocity interact strongly with the wave. The physical
consequences of such an interaction (wave damping in this example) are lost to a
fluid analysis because of the averaging over individual particle velocities.
These shortcomings notwithstanding, a fluid description provides a simpler in-
troduction than kinetic theory to wave characteristics in warm plasmas and we use
it to give an indication of what new modes may arise and to see what modification
of cold plasma modes may occur. We shall assume isotropic pressure and no heat

228 Waves in unbounded homogeneous plasmas
flow; although it is simple enough, in the presence of a strong magnetic field, to
justify a diagonal pressure tensor and no heat flow perpendicular to the magnetic
field, the assumptions of equal parallel and perpendicular pressures and zero paral-
lel heat flow are no more than mathematical expediencies in a collisionless theory.
Thus we add pressure gradients to the equations of motion and use the adiabatic
gas law
p
α
n
−γ
α
α
= const. (6.85)
to close the set of equations as in Table 3.5. The linearized equations are now
∂n
α
∂t
+ n
α0
∇ · u
α
= 0 (6.86)
n
α0
m
α
∂u
α
∂t
+ ∇ p
α
− n
α0
e
α
(E + u
α
× B
0
) = 0 (6.87)
p
α
p
α0
−
γ
α
n
α
n
α0
= 0 (6.88)
and the Maxwell equations (6.11)–(6.14); as before, variables with subscript zero
are equilibrium values and those without subscript are the perturbations. Assuming
plane wave variation ∼ exp i(k ·r −ωt) and eliminating all variables but u
i
and u
e
we arrive, after some tedious but straightforward algebra, at the equations
−ω
2
u
i
+ V
2
i
(k · u
i
)k +
ω
2
pi
(k
2
− ω
2
/c
2
)
k · (u
i
− u
e
)k −
ω
2
c
2
(u
i
− u
e
)
+ i ω
i
(u
i
× b
0
) = 0
(6.89)
−ω
2
u
e
+ V
2
e
(k · u
e
)k +
ω
2
pe
(k
2
− ω
2
/c
2
)
k · (u
e
− u
i
)k −
ω
2
c
2
(u
e
− u
i
)
+ i ω
e
(u
e
× b
0
) = 0
(6.90)
where
V
2
i
=
γ
i
p
i0
n
i0
m
i
=
γ
i
k
B
T
i0
m
i
V
2
e
=
γ
e
p
e0
n
e0
m
e
=
γ
e
k
B
T
e0
m
e
(6.91)
and b
0
is the unit vector in the direction of B
0
.
6.4.1 Longitudinal waves
A simple case which illustrates both finite temperature modification of earlier re-
sults and the emergence of a new warm plasma mode arises when propagation and

6.4 Waves in warm plasmas 229
motion are parallel to B
0
; from (6.87) it follows that E is parallel to k so these are
longitudinal waves. Thus, (6.89) and (6.90) become
(ω
2
− k
2
V
2
i
− ω
2
pi
)u
i
+ ω
2
pi
u
e
= 0 (6.92)
ω
2
pe
u
i
+ (ω
2
− k
2
V
2
e
− ω
2
pe
)u
e
= 0 (6.93)
and the dispersion relation is
(ω
2
− k
2
V
2
i
− ω
2
pi
)(ω
2
− k
2
V
2
e
− ω
2
pe
) − ω
2
pi
ω
2
pe
= 0
with solution
ω
2
=
1
2
(ω
2
p
+k
2
V
2
)
1 ±
1 −
4(k
4
V
2
i
V
2
e
+ k
2
V
2
i
ω
2
pe
+ k
2
V
2
e
ω
2
pi
)
(ω
2
p
+ k
2
V
2
)
2
1/2
(6.94)
Usually V
2
i
V
2
e
, so that the second term in the square root is small and the
solutions are
ω
2
≈ ω
2
p
+ k
2
V
2
(6.95)
ω
2
≈
k
4
V
2
i
V
2
e
+ k
2
V
2
i
ω
2
pe
+ k
2
V
2
e
ω
2
pi
ω
2
p
+ k
2
V
2
(6.96)
The first of these solutions, (6.95), may be further approximated to
ω
2
= ω
2
pe
+ k
2
γ
e
k
B
T
e
/m
e
(6.97)
which is the dispersion relation for electron plasma waves or Langmuir waves and
shows an important change from the cold plasma result. Instead of electron plasma
oscillations we now have longitudinal waves which propagate with group velocity
v
g
=
dω
dk
=
kV
2
ω
The ion terms in (6.95) are negligible compared with the electron terms and like-
wise, from (6.93), the ion flow velocity |u
i
||u
e
|. Essentially, the ions provide a
static neutralizing background for the electron plasma waves.
We now turn to the second solution (6.96) which vanishes in the cold plasma
limit and is, therefore, a new dispersion relation for ion waves. Using (6.91) it may
be written
ω
2
k
2
≈
γ
i
k
B
T
i0
m
i
+
Zγ
e
k
B
T
e0
m
i
(1 + k
2
λ
2
D
)
(6.98)

230 Waves in unbounded homogeneous plasmas
This is the dispersion relation for the ion acoustic wave. However, there is a fun-
damental distinction between this mode and a sound wave in a neutral gas which
propagates on account of collisions. The potential energy to drive the ion acoustic
wave is electrostatic in origin and is due to the difference in amplitudes of the
electron and ion oscillations. In ion acoustic waves ions provide the inertia while
the more mobile electrons neutralize the charge separation.
Finally consider ion waves in the limit ω
2
p
k
2
V
2
e
. In this case (6.96) becomes
ω
2
≈ ω
2
pi
+ k
2
V
2
i
(6.99)
the ion counterpart to electron plasma waves. Comparison with (6.95) shows the
symmetry between ion and electron waves which one would expect from the basic
equations. Note that the retention of the ω
2
pi
term in (6.99) implies T
i0
T
e0
. Also,
from (6.92), we now have |u
e
||u
i
| and the electrons provide a neutralizing
background for the ion plasma oscillations; however, because of their high thermal
velocities they play a dynamic rather than a static role. In fact these observations
are academic since Landau damping restricts the propagation of these waves to a
narrow band of wavelengths such that (T
i0
/T
e0
)
1/2
λ
D
λ λ
D
.
6.4.2 General dispersion relation
The general dispersion relation (which may be obtained from (6.89) and (6.90))
gives six roots for ω
2
corresponding to each wavenumber; these fall naturally into
a high frequency group and a low frequency group. For propagation along B
0
, the
high frequency group consists of RCP and LCP electromagnetic waves and the
longitudinal electron plasma wave.
We shall not draw the CMA diagram for warm plasma waves, as the wave normal
surfaces are now considerably more complicated than in the cold plasma limit.
Instead, a typical (ω, k) dispersion plot is shown in Fig. 6.13 for a low β plasma
with |
e
| <ω
pe
. The high frequency curves come from the Appleton–Hartree
dispersion relation (6.74) in which ion motion and pressure terms are ignored; since
v
p
is large the cold plasma approximation is good. The low frequency curves are
due to Stringer (1963) and refer to a plasma having β = 10
−2
, v
A
/c = 10
−3
,
c
s
/v
A
= 10
−1
, V
i
/c
s
= 0.33 and θ = 45
◦
. The value chosen for β ensures that the
high and low frequency parts of the (ω, k) diagram are well separated.
Stringer obtained the dispersion relation for the three low frequency modes from
the linearized two-fluid equations (6.86)–(6.88) and the Maxwell equations by
combining the ion and electron momentum equations into a one-fluid equation of
motion
ρ
0
∂u
∂t
=−∇ P + j ×B
0
(6.100)
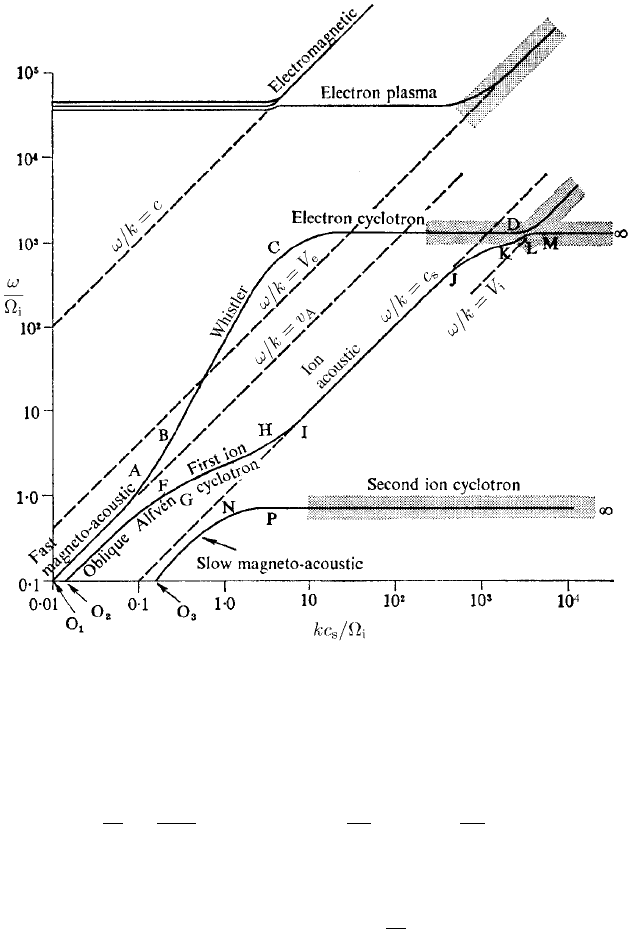
6.4 Waves in warm plasmas 231
Fig. 6.13. Dispersion curves for oblique waves in low β plasma with |
e
| <ω
pe
(after
Stringer (1963)).
where P = p
e
+ p
i
, and a generalized Ohm’s law
∂j
∂t
=
n
0
e
2
m
e
(E + u × B
0
) −
e
m
e
j × B
0
+
e
m
e
∇ p
e
(6.101)
Then from the curl of the induction equation
∇ × ∇ × E = µ
0
∂j
∂t
(6.102)
on neglect of the displacement current. In the derivation of (6.101) terms of order
Zm
e
/m
i
have been ignored but, in fact, this equation may be obtained directly from
(3.70) by taking the ν
c
→ 0 limit; note that σ = n
e
e
2
/m
e
ν
c
.
Now replacing ∇ by ik and ∂/∂t by −iω, (6.102) becomes
iωµ
0
j = k
2
E − (k · E)k (6.103)

232 Waves in unbounded homogeneous plasmas
and substituting this in the left-hand side of (6.101) gives
QE −
c
2
ω
2
pe
(k · E)k + u × B
0
+
ip
e
n
0
e
k −
1
n
0
e
j × B
0
= 0 (6.104)
where Q = (1 + k
2
c
2
/ω
2
pe
).
Next, without loss of generality, we may choose k = (k, 0, 0) and B
0
=
B
0
(cos θ,0, sin θ), so that (6.103) gives
j
x
= 0
E
y
= iωµ
0
j
y
/k
2
E
z
= iωµ
0
j
z
/k
2
(6.105)
and (6.100) gives
u
x
= iB
0
j
y
sin θ/ρ
0
ω(1 − k
2
c
2
s
/ω
2
)
u
y
= iB
0
j
z
cos θ/ρ
0
ω
u
z
=−iB
0
j
y
cos θ/ρ
0
ω
(6.106)
where c
2
s
= (γ
e
p
e0
+γ
i
p
i0
)/ρ
0
and we have used (6.86) and (6.88) to replace P by
P = (γ
e
p
e0
k · u
e
+ γ
i
p
i0
k · u
i
)/ω
= [γ
e
p
e0
(k · u − k · j/n
0
e) + γ
i
p
i0
k · u]/ω
= (γ
e
p
e0
+ γ
i
p
i0
)k · u/ω
since j
x
= 0. Finally, substituting (6.105) and (6.106) in (6.104) yields a vector
equation, involving j as the only unknown, the y and z components of which are
Qµ
0
ω
k
2
−
B
2
0
ρ
0
ω
cos
2
θ +
sin
2
θ
(1 − k
2
c
2
s
/ω
2
)
j
y
+
im
i
B
0
cos θ
eρ
0
j
z
= 0
−
im
i
B
0
cos θ
eρ
0
j
y
+
Qµ
0
ω
k
2
−
B
2
0
cos
2
θ
ρ
0
ω
j
z
= 0
Equating the determinant of the coefficients of this equation to zero gives Stringer’s
dispersion relation
ω
k
4
−
ω
k
2
c
2
s
+ v
2
A
/Q
+ c
2
s
(v
2
A
/Q) cos
2
θ
×
ω
k
2
− (v
2
A
/Q) cos
2
θ
−
ωv
2
A
i
Q
2
ω
2
k
2
− c
2
s
cos
2
θ = 0
(6.107)

6.4 Waves in warm plasmas 233
Table 6.1. Dispersion curves (Fig. 6.13): slow branch
Section Mode Dispersion relation Physical characteristics
O
3
N slow magneto- ω = kc
s
cos θ E almost longitudinal
acoustic kc
s
i
coupling electron and
ion fluids
P∞ second ion ω =
i
cos θ longitudinal wave
cyclotron kc
s
i
E k
Table 6.2. Dispersion curves (Fig. 6.13): intermediate branch
Section Mode Dispersion relation Physical characteristics
O
2
F oblique ω = kv
A
cos θ P < 0
Alfv
´
en ω
i
GH first ion ω =
i
[1 + (k
2
c
2
s
/
2
i
) sin
2
θ P =−1: Below
i
cyclotron −(
2
i
/k
2
v
2
A
)(1 + sec
2
θ)]
1/2
magnetic energy
c
s
i
/(v
A
cos θ) kc
s
∼
i
drives the wave;
above
i
plasma
pressure dominates
IJ ion ω = kc
s
longitudinal wave
acoustic
i
< kc
s
<ω
pi
E k
The waves and approximate dispersion relations corresponding to the three low
frequency branches (labelled slow, intermediate and fast) are given in Tables 6.1–
6.3. Conditions which apply throughout the tables are c
2
s
v
2
A
and m
e
/m
i
cos
2
θ.
The first thing to note in Fig. 6.13 is the appearance of the additional, slow
branch (O
3
NP∞), corresponding to the slow magnetoacoustic wave discussed in
Section 4.8. We have seen already that the cold plasma modes at low frequencies
correspond to the fast magnetoacoustic and intermediate, shear Alfv
´
en waves. In
fact, we can recover the results of Section 4.8 from (6.107) by taking the low
frequency limit ω
i
. In this case the (ω/
i
)
2
term may be neglected leaving
a dispersion relation equivalent to (4.121) but with v
2
A
/Q replacing v
2
A
. However,
for c
2
s
v
2
A
the slow mode has ω ≈ kc
s
cos θ, independent of v
A
, while the
other two modes have ω ∼ kv
A
, so that c
2
k
2
/ω
2
pe
Zm
e
/m
i
giving Q ≈ 1,
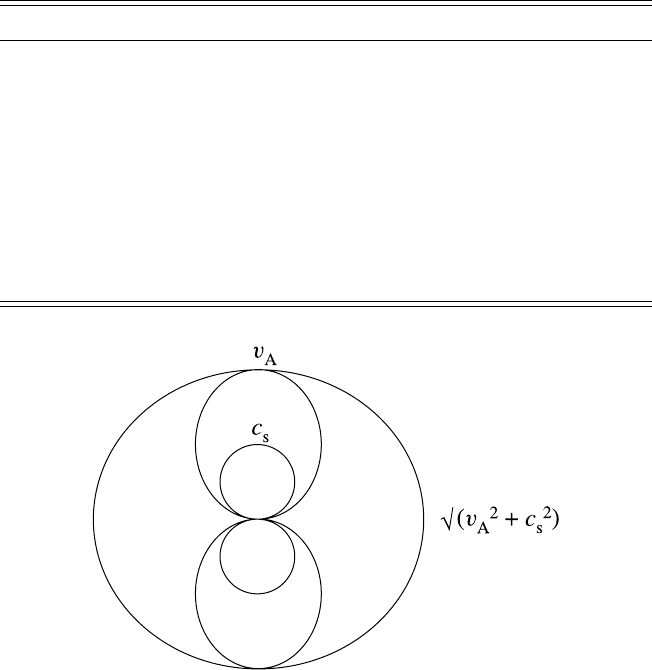
and the solutions (4.122) and (4.123) are recovered. The wave normal surfaces for
these waves in the ideal MHD approximation and for c
s
<v
A
are sketched in
Fig. 6.14.
234 Waves in unbounded homogeneous plasmas
Table 6.3. Dispersion curves (Fig. 6.13): fast branch
Section Mode Dispersion relation Physical characteristics
O
1
A fast magneto- ω = k(v
2
A
+ c
2
s
sin
2
θ)
1/2
P > 0
acoustic ω
i
BC whistler ω (k
2
v
2
A
/
i
) cos θ P ≈+1; for ω>
i
ion
i
kv
A
cos θ role decreases on
account of inertia
CD electron ω |
e
|cos θ P =+1; electron velocity
cyclotron |
e
| <ω
pe
increase ⊥ B
0
is
limited by increase B
0
to maintain charge
neutrality
Fig. 6.14. Phase velocity surfaces of MHD waves for v
A
> c
s
.
Let us now examine what happens as we approach the ion cyclotron frequency.
For the cold plasma we know that the intermediate wave disappears as the reso-
nance, which is at θ = π/2 for ω
i
, approaches θ = 0asω →
i
. To find
the resonances of the low frequency warm plasma waves we let k →∞in (6.107)
giving
ω
2
=
2
i
cos
2
θ(1 − c
2
ω
2
/v
2
A
ω
2
pe
cos
2
θ)
2
which, ignoring terms of order m
e
/m
i
, has the solutions
ω =
i
cos θ, ω =|
e
|cos θ (6.108)
6.4 Waves in warm plasmas 235
Now, writing (6.107) as
ω
k
6
−
ω
k
4
c
2
s
+ (v
2
A
/Q)(1 + cos
2
θ)
+
ω
k
2
(v
2
A
/Q) cos
2
θ
2c
2
s
+ (v
2
A
/Q)
1 −
ω
2
2
i
+
v
4
A
c
2
s
cos
2
θ
Q
2
2
i
(ω
2
−
2
i
cos
2
θ) = 0
we may neglect the last term in the neighbourhood of the resonance at ω =
i
cos θ
and solve the resulting bi-quadratic for the other two modes, obtaining
ω
2
k
2
≈ c
2
s
+ v
2
A
(1 + cos
2
θ) (6.109)
and
ω
2
k
2
≈
v
2
A
cos
2
θ[2c
2
s
+ v
2
A
(1 − ω
2
/
2
i
)]
c
2
s
+ v
2
A
(1 + cos
2
θ)
(6.110)
Here we have again put Q = 1 since c
2
k
2
/ω
2
pe
∼ Z
2
m
e
/m
i
1. We can identify
these modes by letting c
s
→ 0 in which case (6.109) reduces to (6.70) for the
compressional Alfv
´
en wave and (6.110) to (6.71) for the ion cyclotron wave. Thus,
(6.109) is the dispersion relation for the fast magnetoacoustic wave and (6.110) is
for the shear Alfv
´
en–ion cyclotron mode at ω ≈
i
cos θ. The interesting point
about (6.110) is that the resonance stays at θ = π/2asω →
i
and does not
migrate towards θ = 0. Consequently, there is no destructive transition at
i
and
the mode persists for ω>
i
. The sharp reduction in v
p
due to the vanishing
of the second term in the square bracket in (6.110) at ω =
i
gives rise to a
so-called pseudo-resonance, indicated by the GH section of the intermediate wave
dispersion curve in Fig. 6.13. The mode is called the first ion cyclotron wave in this
region (ω ≈
i
) to distinguish it from the slow wave, which has a true resonance
(ω ≈
i
cos θ for all k so v
p
→ 0ask →∞for all θ)atω =
i
, and is
called the second ion cyclotron wave. Thus, consideration of finite temperature has
(i) introduced the slow magnetoacoustic wave which then disappears at the ion
cyclotron resonance and (ii) demonstrated the continuation of the shear Alfv
´
en–
first ion cyclotron mode to frequencies above
i
.
To find approximate dispersion relations for the fast and intermediate modes
between the ion and electron resonances we may take
i
ω |
e
|. Since
ω/k ∼ c
s
or v
A
all terms in (6.107) are of similar magnitude except for the last one
which has the factor (ω/
i
)
2
. Thus, dropping all terms but this, one solution is
ω
2
= k
2
c
2
s
(6.111)
236 Waves in unbounded homogeneous plasmas
i.e. the ion acoustic wave. Then rewriting (6.107) in the form
ω
k
6
−
ω
k
4
[c
2
s
+ (v
2
A
/Q)(1 + cos
2
θ)] +
ω
k
2
(2c
2
s
+ v
2
A
/Q)(v
2
A
/Q) cos
2
θ − c
2
s
(v
4
A
/Q
2
) cos
4
θ +
ω
i
2
c
2
s
−
ω
k
2
(v
4
A
/Q
2
) cos
2
θ = 0
we may neglect the third and fourth terms compared with the final term and,
anticipating that the second solution for c
2
s
v
2
A
has ω/k v
A
, we may also
drop the second term and the c
2
s
in the final term leading to the result
ω ≈
k
2
v
2
A
cos θ
i
=
k
2
c
2
|
e
|cos θ
ω
2
pe
(6.112)
where we have again put Q = 1 since k
2
c
2
/ω
2
pe
∼ ω/|
e
|1. This is the general-
ization for non-zero θ of (6.55), the dispersion relation for the whistler wave. Thus,
between the resonances the intermediate wave emerges from the pseudo-resonance
and propagates at a reduced phase velocity as an ion acoustic wave while the fast
wave follows its cold plasma behaviour becoming a whistler.
As the electron cyclotron resonance at ω =|
e
|cos θ is approached the pat-
tern of behaviour seen at the ion cyclotron resonance is repeated. The slower
(intermediate) wave suffers the destructive transition, which in the cold plasma
was the fate of the fast wave, while the fast wave undergoes a pseudo-resonance
and survives to continue propagation above ω =|
e
|, but at the reduced phase
velocity ω/k = V
i
. Both of these occurrences can be attributed to the appearance
of the new, longitudinal, warm plasma mode discussed in Section 6.4.1; see (6.96).
The coupling of transverse and longitudinal waves that occurs for θ = 0 enables
the first ion cyclotron wave to emerge from the ion cyclotron resonance as the
ion acoustic wave (6.98). Likewise, the electron cyclotron wave emerges from the
electron cyclotron resonance as the ion plasma wave, the mode described by (6.99).
Longitudinal modes are not well described by (6.107) for the neglect of the dis-
placement current in its derivation implied k·j = 0, i.e. zero space charge. Stringer,
therefore, derived an electrostatic dispersion relation from which the approximate
results (shown in the tables) in the neighbourhood of these transitions are found.
For sufficiently low β plasmas ω
pe
< |
e
| and the high and low frequency
branches overlap. For such cases (6.107) becomes invalid at the overlap, i.e. for
ω>ω
L
∼ ω
2
pe
/|
e
|. An example is shown in Fig. 6.15 in which Stringer used the
Appleton–Hartree dispersion relation (6.74) to calculate the curve for the fast wave
for ω>ω
2
pe
/|
e
|.
