Бондаренко В.В. Основы теории цепей. Часть 2
Подождите немного. Документ загружается.

41
=
−
−
+
−
(5)
|
|
<|
|
(
0
)
=
−
−
+
−
=
=
−
(
−
)
(
−
)
= −
= −
б) Критический режим.
2
=
1
2
=
1
√
=
2
√
=2
=
кр
3)
св
−?
св
=
+
=
=
4)
=
пр
+
св
=0+
+
u
L
t
B
5
i(0)=0
–B
6
–U
42
=
=
(
+
+
)
=
0=
(
+
)
=
=−
=−
=
−
(2)
=
=
(
−
−
)
= −
= = −
=
= −
−
= −
( −1)
в)
2
<
1
= − ±
−
= − ±
−
= − ±
=
−
3)
св
=
sin
+
4)
=
пр
+
св
=0+
sin
+
=
=
(
−
)
sin
+ +
cos
+
= sin
0=
(
−
)
sin +
cos
sin =
cos
tg
=
(3)
43
=
arctg
(4)
=
sin
sin
(
+
)
(5)
а)
(
0
)
=
sin
sin =
б)
=
=
sin
(
−
)
sin
+ +
+
sin
cos(
+ )
=
= −
sin
sin
+ −
cos
+ =
= −
sin
+
sin(
+ + )
= −
= −
=
−
sin
sin
=
−
sin
(6)
i
t
I
m
i(0
–
)=i(0
+
)
u
c
t
U
–
U
T

44
=
sin
(7)
) ⊖
б)
=
=
−
sin
(8)
=
= −
(
−
)
sin
−
cos
=
=
sin
−
cos
=
=
+
sin
+ =
=
sin
− =
=
sin
sin
−
(9)
a)
(
0
)
=
sin
sin
(
−
)
= −
б)
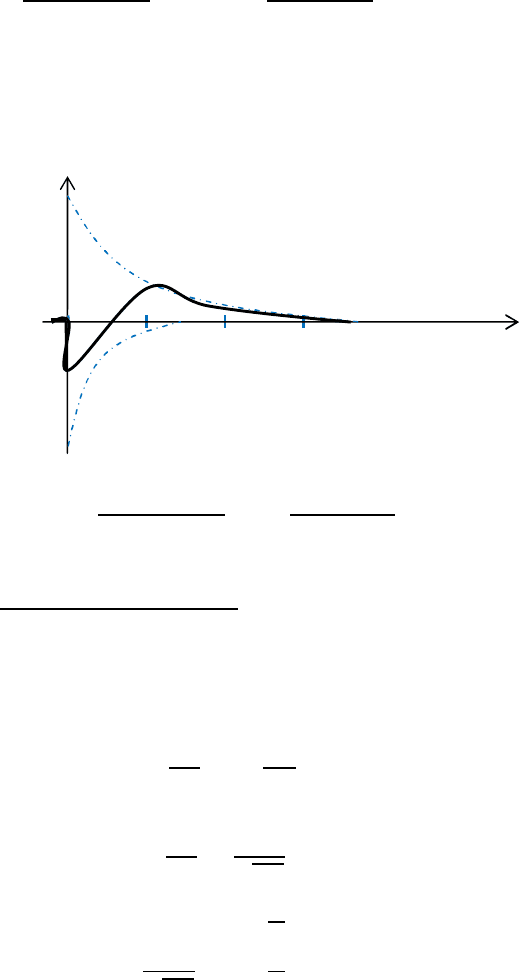
Видим для любого момента времени
+
+
=0.
u
L
t
U
T

45
Глава 2. Операторный метод
расчёта переходных процессов
§2.1. ОПЕРАТОРНЫЙ МЕТОД РАСЧЁТА ПЕРЕХОДНЫХ
ПРОЦЕССОВ
Сложность и трудоёмкость классического метода заключается в
пункте 4, в котором мы находим постоянные интегрирования. В
отличие от классического метода, в операторном методе нену-
левые начальные условия мы записываем в исходную цепь и
решаем одной системой уравнений.
1) Оригиналу соответствует изображение
(
)
≓ ( ), = + .
2) Задача решается в операторной форме. Находятся
(
)
,
(
)
,
( )…
3) Делается обратный переход
(
)
≓ ( ).
Если при <0
(
)
=0, а при t ≥ 0 выполняются условия Ди-
рихле, интеграл
(
)
=
∫
(
)
сходится. Это прямое пре-
образование Лапласа.
Обратное преобразование Лапласа:
(
)
=
∮
(
)
.
§2.2. ИЗОБРАЖЕНИЯ НЕКОТОРЫХ ФУНКЦИЙ
1)
(
)
= .
(
)
=
(
)
=
=
=
−
|
=
=
⋅
−1
|
=
≓
46
Например, =30 ≓
(
)
=30
⁄
.
2)
(
)
=
(
)
=
=
(
)
=
(
)
−
(
−
)
|
=
1
(
−
)
≓
1
−
≓
1
+
3)
(
)
= =
sin
(
+
)
(
)
→
(
)
(
)
=
̇
̇
=
( )
≓
(
)
=
̇
−
=
−
§2.3. СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
1) ⋅
(
)
≓ ⋅ ( )
2)
∑
( )
≓
∑
( )
Сумме оригиналов соответствует сумма их изображений.
3)
∑
(
)
≓
∑
(
)
Сумме оригиналов с коэффициентами
соответствует сумма
изображений с этими коэффициентами.
Всё это вытекает из свойства линейности преобразования Лап-
ласа.
4) Теорема запаздывания:
(
−
)
≓
(
)

47
§2.4. ИЗОБРАЖЕНИЯ ФУНКЦИЙ, СВЯЗАННЫХ С
ДИФФЕРЕНЦИРОВАНИЕМ И ИНТЕГРИРОВАНИЕМ
(
)
≓
(
)
−
(
0
)
(1)
=
≓
(
)
−
(
0
)
=
( )
(
)
=
(
)
⋅
−
(
0
)
(2)
Если начальные условия нулевые, нетрудно получить закон
Ома в операторной форме ( → ).
(
)
=
(
)
(3)
= +
Символический метод — частный случай операторного.
Другой пример.
=
≓
(
)
−
(
0
)
=
(
)
(
)
=
(
)
−
(
0
)
(4)
Если начальные условия нулевые
(
0
)
=0, то
(
)
=
(
)
1
→
1
=
(
)
≓
(
)
(5)
=
(
0
)
+
1
≓
(
0
)
+
1
(
)
=
(
)
48
(
)
=
(
)
+
(
0
)
(6)
=
(
0
)
+
1
≓
(
0
)
+
1
(
)
=
(
)
(
)
=
(
)
1
+
(
0
)
(7)
§2.5. ЗАКОН ОМА В ОПЕРАТОРНОЙ ФОРМЕ
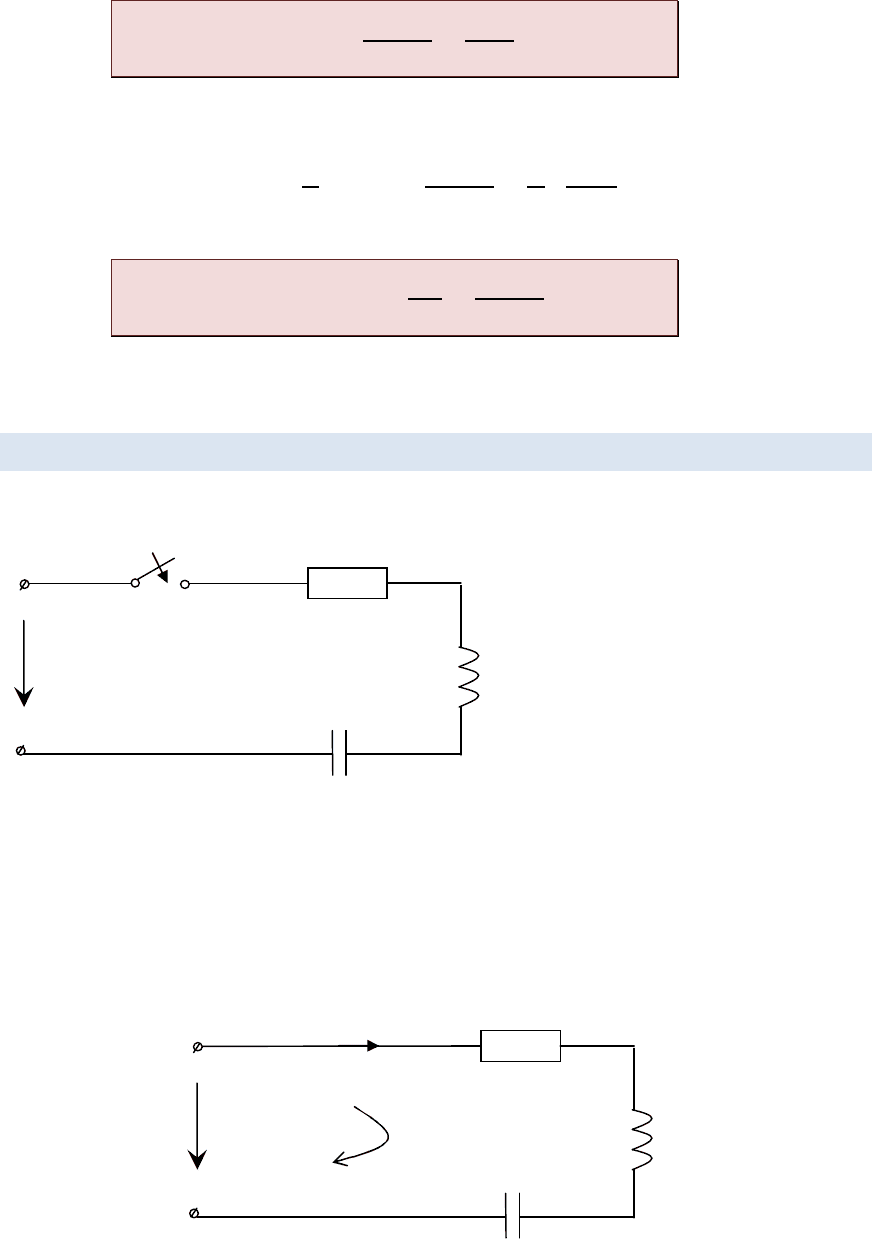
U, R, L, C
начальные условия —
нулевые
———————————
i
Для цепи после коммутации составим исходное уравнение по
второму закону Кирхгофа.
+
+
=
L
R
U
C
i
L
R
U
C
K
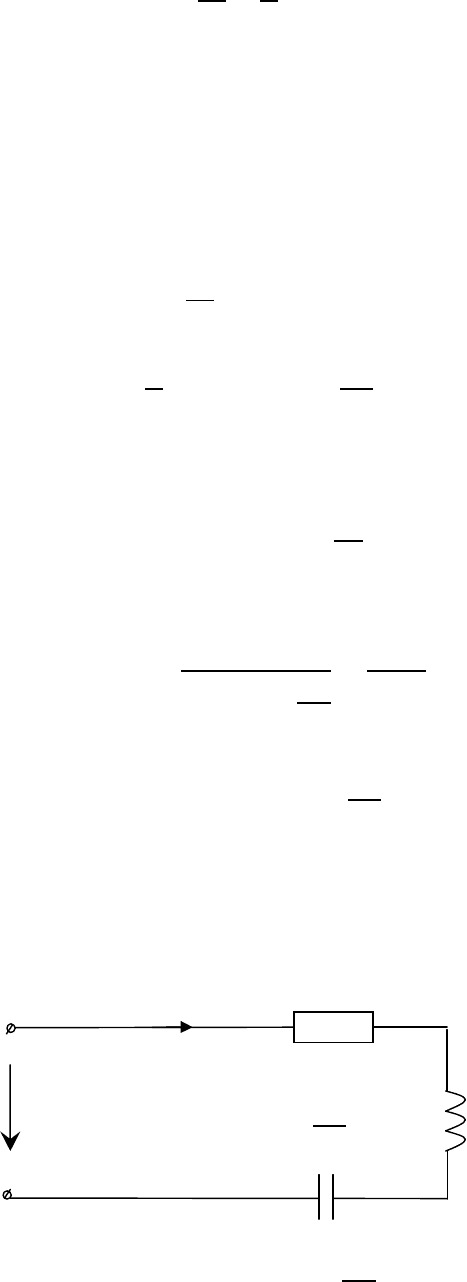
49
+
+
1
=
(1)
≓
(
)
≓
(
)
≓
(
)
≓
(
)
⋅
1
≓
(
)
⋅
1
Подставим в уравнение (1).
(
)
+
(
)
+
(
)
1
=
(
)
(3)
(
)
=
(
)
+
+
1
=
(
)
(
)
(4)
(
)
=
+
+
1
(5)
— полное сопротивление цепи в операторной форме.
Схема в операторной форме следует из уравнений (3) и (4):
→ , →
1
pL
R
U(p)
1
I(p)
50
→
(
)
→
(
)
→
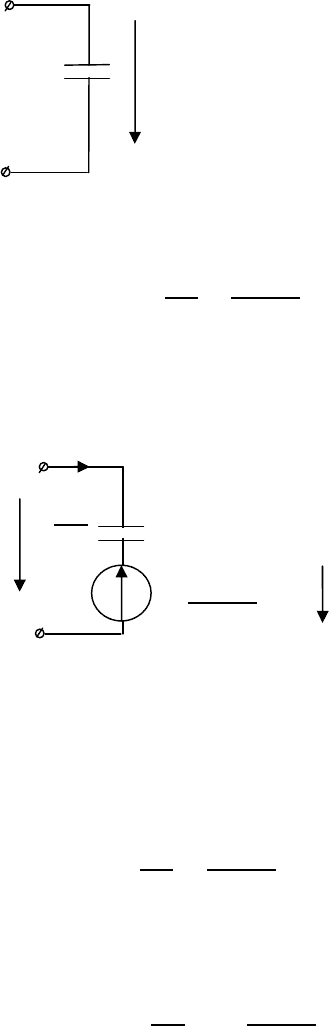
Ненулевые начальные условия
1. Конденсатор
Используем уравнение (7) предыдущего параграфа.
(
)
=
(
)
⋅
1
+
(
0
)
Этому уравнению будет соответствовать схема:
Полярность определяется полярностью исходного элемента.
Как источник напряжения:
−
(
)
+
(
)
1
+
(
0
)
=0
Как источник ЭДС:
−
(
)
+
(
)
1
= −
(
0
)
1
(
0
)
≠
0
(
)
+
–
C
(
0
)
≠
0
(
)
