Бондаренко В.В. Основы теории цепей. Часть 2
Подождите немного. Документ загружается.


31
В выражение (2) подставим 0.
(
0
)
= +
(
−
)
−
=0
=
=
−
−
−
=
=
−
−
−
(3)
|
|
=
|
|
Первый закон коммутации выполняется.
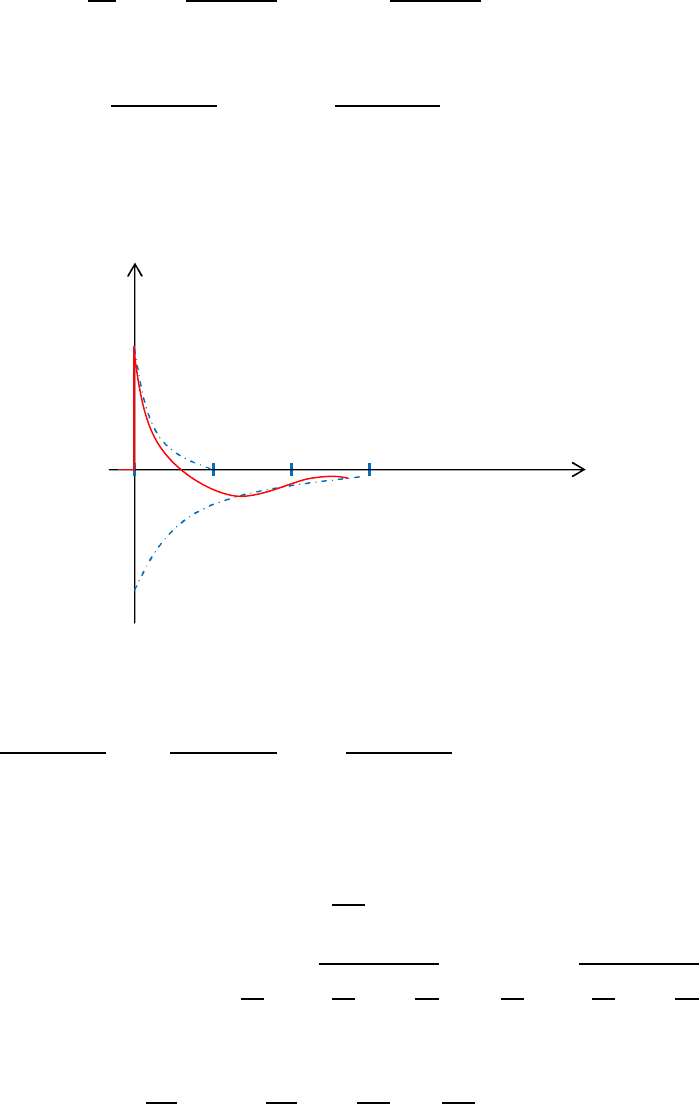
i
τ
–B
4
B
3
u
c
τ
U
–B
1
+B
2
32
=
(4)
=
=
−
−
−
=
=
−
−
−
(5)
|
|
<
|
|
Подставим ноль в выражение (5), то есть найдём
(0).
(
0
)
=
−
−
−
=
−
(
−
)
=
Покажем, что
=1.
=
1
Из уравнения (1)
= −
+
−
−
−
−
2
−
2
−
1
=
1
б) Критический режим.
u
L
τ
–B
5
B
6

33
=
−
2
±
2
−
1
(1)
2
=
1
=
2
√
=2
=
кр
св
=
+
4)
=
пр
+
св
= +
+
=
=
(
+
+
)
0= +
0=
(
+
)
=−
=−
=
=
−
+
(2)
=
=
(
−
+
+
)
=
= =
=
=
(
+
)
в) Колебательный режим работы цепи.
=
−
2
±
2
−
1
(1)
= − ±
−
= − ±
=
2
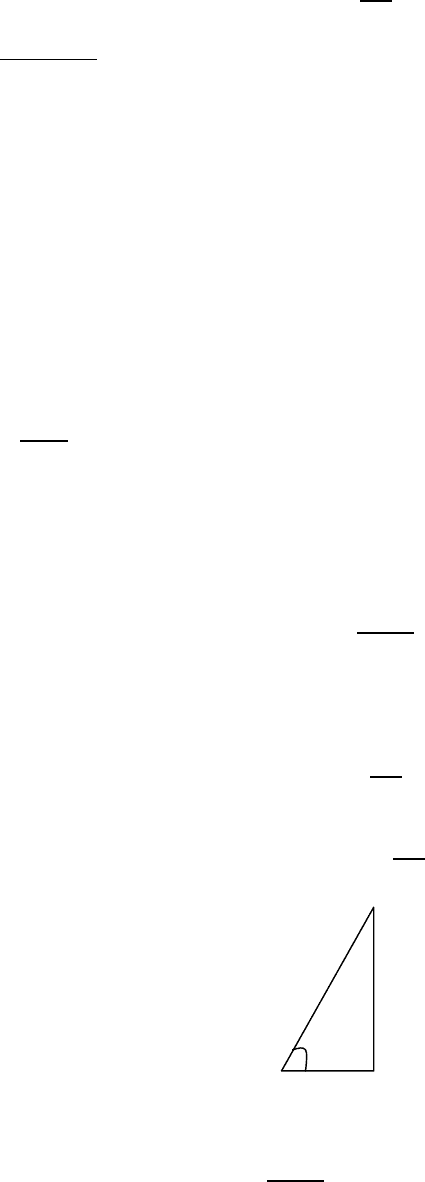
34
=
1
=
−
— частота затухающих колебаний контура.
3) В этом случае удобно искать свободную составляющую в
форме затухающего синуса:
св
=
sin(
+ )
4)
=
пр
+
св
= +
sin
+
=
=
(
−
)
sin
+ +
cos
+
0= + sin
0=
(
−
)
sin +
cos
=
−
sin
(2)
sin =
cos
tg
=
(3)
=
(4)
=
−
sin
sin
+
св
(5)
Построим уравнение (5).
ω
f
δ
ω
0
θ

35
а)
св
(
0
)
= −
sin
sin
(
)
= −
б)
в)
= +
св
Найдём ток
=
= −
sin
(
−
)
sin
+ −
−
sin
cos
+
=
=
sin
sin
+ −
cos
+ =
=
sin
+
sin(
+ + )
sin + cos = sin
(
+
)
=
+
; tg =
; =arctg
tg = −
=
sin
sin
=
sin
(6)
=
sin
(7)
u
c
t
–U
U
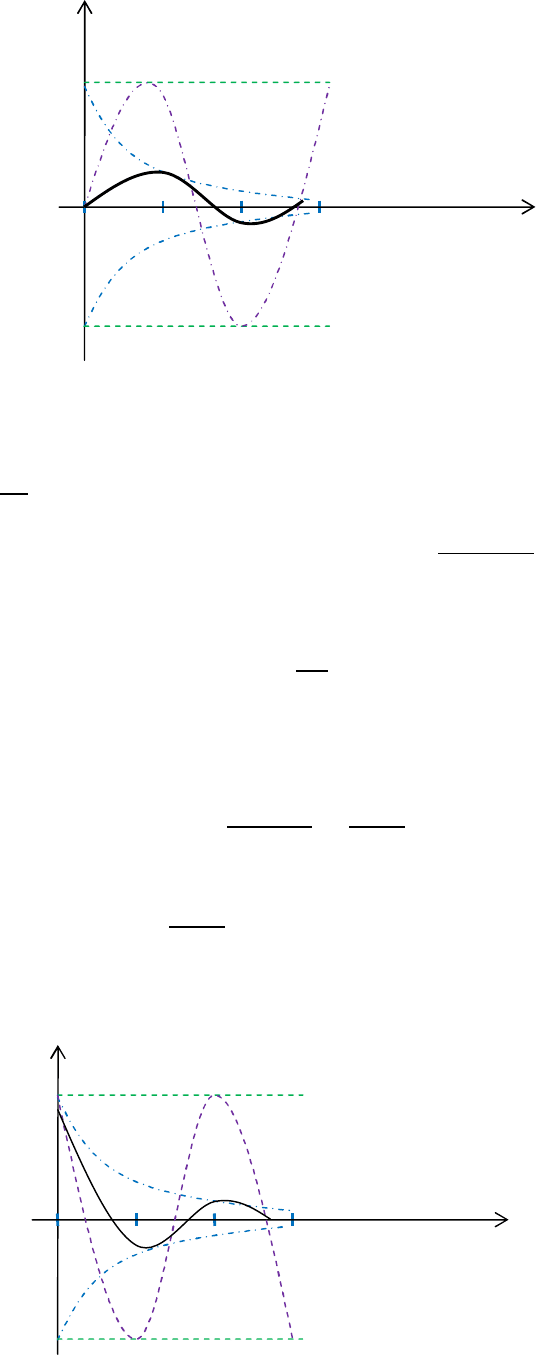
36
=
=
sin
(8)
=
=
(
−
)
sin
+
cos
=
= −
sin
−
cos
= −
+
sin
+
tg = −
= −
sin
−
=
sin
=
sin
=
−
sin
sin
−
(9)
u
L
t
U
i
t
i(0)=0

37
а)
(
0
)
= −
sin
sin
(
−
)
= .
б) Учтём затухающий множитель
.
Выводы.
1) Мы исходили из уравнения
+
+
= . Оно верно для
любого момента времени,
(0)
0
+
(0)
+
(0)
0
=
2) Δ =
=
( )
=
Δ — декремент затухания. Определяется как отношение двух
амплитуд через период.
3) Логарифмический декремент затухания:
lnΔ =
=
lnΔ
§1.13. КОРОТКОЕ ЗАМЫКАНИЕ RLC-ЦЕПИ
,
,
,
—————————
,
,
,
До коммутации:
(
0
)
=
(
0
)
=0
(
0
)
=
(
0
)
=
L
R
U
C

38
После коммутации:
+
+
=0
+
+
=0
=
+
+
=0
2)
=
пр
+
св
пр
=0
3)
св
= ?
св
+
св
+
св
=0
+ +1=0
+
+
1
=0
L
R
i
C
u
c
(0) ≠ 0
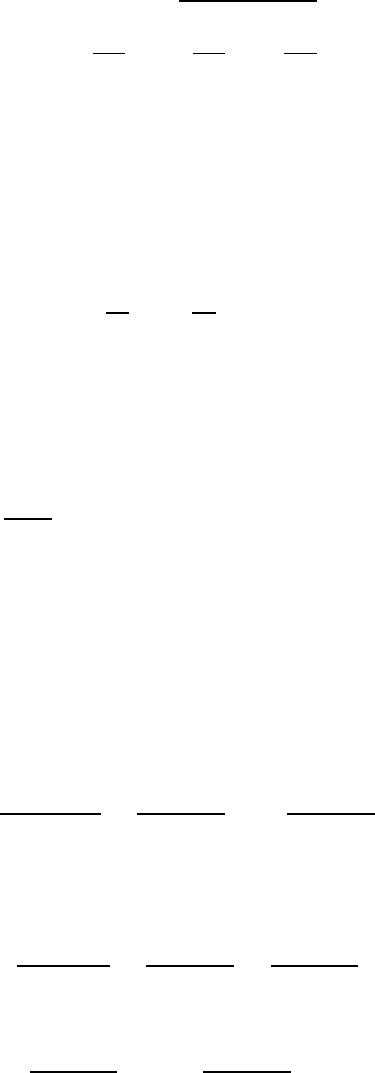
39
=
−
2
±
2
−
1
(1)
Если первое слагаемое под корнем больше второго — аперио-
дический режим. Если оба слагаемых одинаковы, корни крат-
ные — критический режим. Если первое слагаемое меньше
второго — колебательный режим.
а) Апериодический режим.
>
св
=
+
4)
=
пр
+
св
=0+
+
=
=
(
+
)
=
+
0=
(
+
)
+
=
+
=0
=
1
0
1 1
=
−
= −
−
=
1
0
−
=
−
−
=
−
=
−
−
+
−
=
(2)
=+
−
|
|
>
|
|
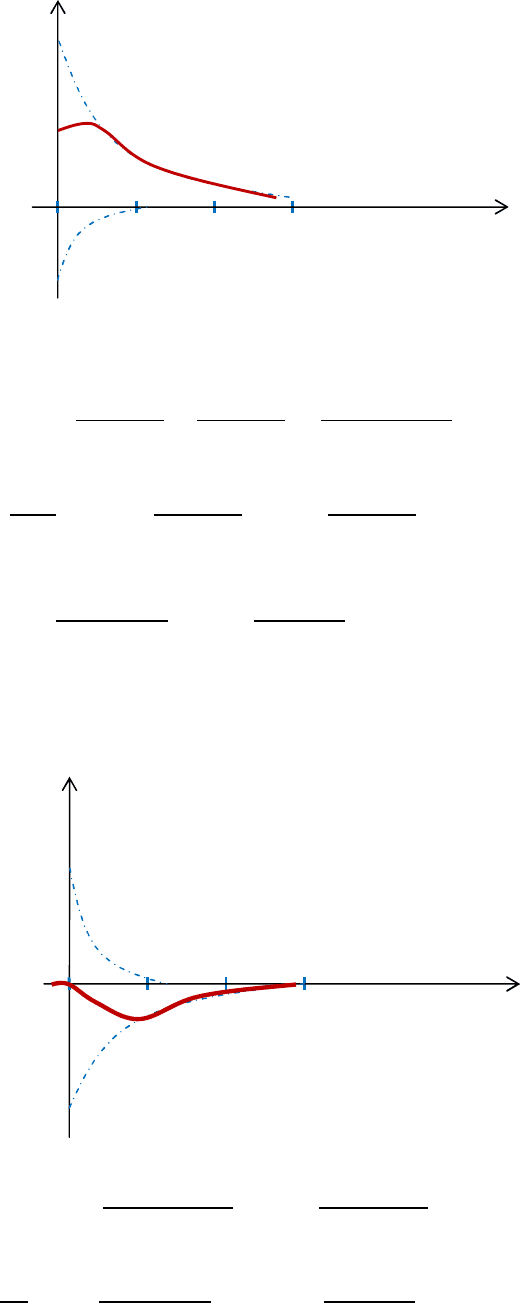
40
Докажем, что
(
0
)
= .
(
0
)
= −
−
+
−
=
(
−
)
−
=
=
= −
−
+
−
=
=
−
−
+
−
=
(3)
= −
+
= =
−
−
+
−
=
=
−
−
+
−
=
i
t
B
4
i(0)=0
u
c
t
B
1
–B
2
–B
3
