Boggs S. Principles of Sedimentology and Stratigraphy
Подождите немного. Документ загружается.


The grain size of particles in consolidated sedimentary rocks that cannot be
disaggregated must be measured by teciques other than sieving or sedimenta
tion analysis. e size and sorting of sand- and silt-size particles can be estimated
by using a reflected-light binocular microscope and a standard size-comparison
set, which consists of grains of specific sizes mounted on a card. More accurate
size determination can be made by measuring grains in thin sections of rock by
of a transmitted-light petrographic microscope fitted with an ocular microme
r or by the image analysis technique mentioned above. Both microscopic and
image analysis techniques tend to yield grain sizes that are smaller than the
maximum diameter of the grains because the plane of a thin section does not cut
exactly through the centers of most grains. Grain sizes measured by these meth
ods are commonly corrected mathematically in some way to make them agree
more closely with sieve data (Burger and Skala, 1976; Piazzola and Cavaroc, 1991).
Fine silt- and day-size grains in consolidated rocks may be studied by use of an
electron microscope, although the electron microscope is not commonly used for
grain-size measuments.
Graphical and Mathematical Treatment of Grain-Size Data
Measurement of grain size by the techniques described generates large quantities
of data that must be reduced to a more condensed form before ey can be used. Ta
bles
of data showing the weights of grains in various size classes must be simpli
ed to yield such average properties of grain populations as mean grain size and
sorting. Both graphical and mathematical data-reduction methods are in common
. Graphical plots are simple to construct and provide a readily understandable
visual representation of grain-size distributions. On the other hand, mathematical
methods, some of which are based on itial graphical treatment of data, yield sta
tistical grain-size parameters that may be useful in enviroental studies.
Gphical Plots
Figure 3.1 illustrates three common graphical methods for presting grain-size
data. Figure 3.1A shows typical grain-size data obtained by sieve analysis. Raw
sie ve weights are first converted to individual weight percents by dividing the
weit in each size class by the total weight. Cumulative weight percent may be
calculated by adding the weight of each succeeding size class to the total of the
preceding classes. Figure 3.1B shows how individual weight percent can be plot
d as a function of grain size to yield a grain-size histogram-a bar diagram in
which grain size is plotted along the abscissa of the graph and individual weight
percent along the ordinate. Histograms provide a quick, easy, pictorial method for
representing grain-size distributions because the approximate average grain size
and the sorting-the spread of grain-size values around the average size-can be
seen at a glance. Histograms have limited application, however, because the shape
of e histogram is affected by the sieve interval used. Also, they cannot be used to
obin mathematical values for statistical calculations.
A frequency curve (Figure 3.1B) is essentially a histogram in which a smooth
rve takes the place of a discontinuous bar graph. Connecting the midpoints of
ea
ch size class in a histogram with a smooth curve gives the approximate shape of
frequency curve. A frequency curve constructed in this manner does not, how
ever, accurately fix the position of the highest point on the curve; this point is im
portant for determining the modal size, to be described. A grain-size histogram
plotted fm data obtained by sieving at exceedingly small sieve intervals would
yield e approximate shape of a frequency curve, but such small sieve intervals
are not practical. Accurate frequency curves can be derived from cumulative
curves by special graphical methods described in detail by Folk (1974).
3.2 Grain Size
55

56
Chapter 3 I Sedimentary Textures
Figure 3.1
Common visual methods
of displaying grain-size
data. A. Grain-size data
table. B. Histogram and
frequency curve plotted
from data in A. C. Cumula-
tive cue with an arith-
metic ordinate scale. D.
Cumulative curve with a
probability ordinate scale.
A B
Raw
Individual
Cumulative
Size
weight (gm)
weight percent
weight percent
18
-1.0
0.43
0.5
0.5
c
-0.5
2.13
2.5
3.0
0.0
4.25
5.0
8.0
14
frequency
0.5
6.80
8.0
16.0
.
/
curve
1.0
9.35
11.0 27.0
10
1.5
12.75
15.0 42.0
�
2.0
13.58
16.0 58.0
2.5
12.75
15.0
73.0
6
3.0
9.35
11.0
84.0
·
3.5
6.80 8.0 92.0
2
4.0
4.25
5.0
97.0
5
4.5
2.13
2.5
99.5
-1
0 2
3
4
5
5.0
0.43
0.5
100.0
85.00
Size
c D
100 100
c
c
80
0
w
W
-
90
:�
- 0
60
��
"i
.
�
50
�
E
40
��
.:
10
- 0
�
-
s
-
E
20
E
0
0
-1
0
2 3
4
5
-1
0
2 3
4
5
Size Size
A grain-size cumulative curve is generated by plotting grain size against cu
mulative weight percent frequency. The cumulative curve is the most useful of the
grain-size plots. Although it does not give as good a pictorial representation of
the grain-size distribution as does a histogram or frequency curve, its shape is
virtually independent of the sieve interval used. Also, data that can be derived
from the cumulative curve allow calculation of several important grain-size sta
tistical parameters. A cumulative curve can be plotted on an arithmetic ordinate
scale (Fig. 3.1C) or on a log probability scale in which the arithmetic ordinate is re
placed by a log probability ordinate (Fig. 3.10). When phi-size data are plotted on
an arithmetic ordinate, the cumulative curve typically has the 5-shape shown
Figure 3.1C. The slope of the central part of this curve reflects the sorting of the
sample. A very steep slope indicates good sortg, and a very gentle slope poor
sorting. If the cumulative curve is plotted on log probability paper, the shape of
the curve will tend toward a straight line if the population of grains has a normal
distribution (actually log-normal, as illustrated in Figure 3.1D).ln a normal distri
bution, the values show an even distribution, or spread, about the average value.
conventional statistics, a normally distributed population of values yields a
perfect bell-shaped curve when plotted as a frequency curve. Deviations from
normality of a grain-size distribution can thus be easily detected on log probabili
ty plots by deviation of the cumulative curve from a straight line. Most natural
populations of grains in siliciclastic sediments or sedimentary rocks do not have a
normal (or log-normal) distribution; the nearly normal distribution shown in
Figure 3.1B is not typical of natural sediments. Some investigators believe that the
shape of the log probability curve reflects conditions of the sediment transport
process and thus can be used as a tool enviromnental terpretation. We shall
return to this point subsequently.

Graphical plots permit quick, visual inspection of the grain-size charac
teristics of a given sample; however, comparison of graphical plots becomes
cumbersome and inconvenient when large numbers of samples are involved.
Also, average grain-size and grain-sorting characteristics cannot be deter
mined
very accurately by visual inspection of grain-size curves. To overcome
these disadvantages, mathematical methods that permit statistical treatment
of grain-size data can be used to derive parameters that describe grain-size
distributions in mathematical language. These statistical measures allow both
the average size and the average sorting characteristics of grain populations to
be expressed mathematically. Mathematical values of size and sorting can be
used to prepare a variety of graphs and charts that facilitate evaluation of
grain-size data.
Mathematical Measures
Average Grain Se. ree mathematical measures of average grain size are com
mon use. The mode is the most frequently occurrg particle size in a population of
. e diameter of the modal size corresponds to the diameter of grains p
by the steepest pot (inflection point) on a cumulative curve or the ghest
point on a equency curve. Siliciclastic sediments and sedimentary rocks tend to
have a single modal size, but some sediments are bimodal, with one mode the
end of the se disibution and one in the fine end. Some are even poly
modal. The median size is e midpoint of the gra-size distribution. Half of the
ins by weit are larger than the median size, and half are smaller. The median
size corresponds to e 50 percentile diameter on the cumulative curve (Fig. 3.2).
e mean size is the aritetic average of all the particle sizes in a sample. The true
aritetic mean of most sediment samples cannot be determined because we can
not count the total number of grains a sample or measure each small gra. ap
pximaon of the arimetic mean can arrived at by pickg selected percentile
values om the cumulative curve and averagg these values. As shown in Figure
3.2 and Ta ble 3.3, the 16th, 50th, and 84th percenle values are coonly used for
calculation. The mode, medi, and mean sizes may or may not be the same, as
ssequeny discussed under the topic of skewness (e.g., Fig. 3.5).
ing. The sorting of a grain population is a measure of the range of grain sizes
present and the magnitude of the spread or scatter of these sizes around the mean
size. Sorting can be estimated the field or laboratory by use of a hand lens or
100
80
c
�
�g
ad1
>
�
40
E
0�
20
0
Figure 3.2
3.2 Grain Size
57
-1
0
2
Size
3
4
5
Method for calculating percentile values from the cumulative
curve.

58
Chapter 3 I Sedimentary Textures
Fire 3.3
ble 3.3 Foulas
for calating grainize
statiscalp
�
�
�
by apcal methods
·
Graphic mean
Inclusive graphic
standard deviation
Inclusive graphic skewness
Graphic kurtosis
g- t6
qs - s
• = -··--- ··
-··--
I
4
( <P9s - s)
�
-------------�
2.44( 7s 2sl
6.6
(1)
(2)
(3)
(4)
urce: fnlk, R. L1 nd W. C Ward, 1957, Br,zn: River bar: A �tudy in the significance ()f grain-::�ize parilmeters: Jour
Sc1f. Petrology, v. 27, p. 3-26.
microscope and reference to a visual estimation chart (Fig. 3.3). More accurate de
termination of sorting requires mathematical treatment of grain-size data. The
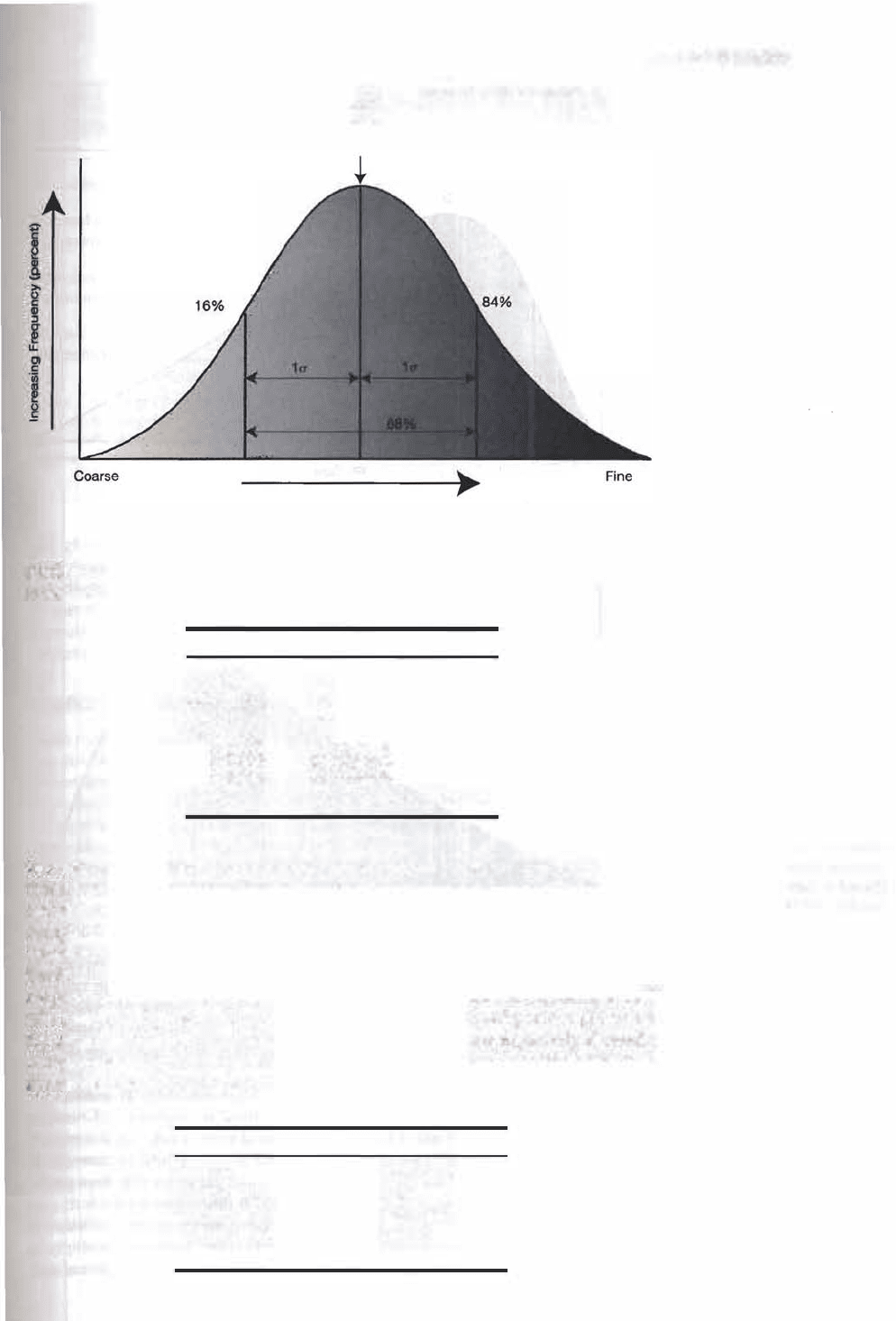
mathematical expression of sorting is standard deviation. In conventional statis
tics, one standard deviation encompasses the central 68 percent of the area under
the frequency curve (Fig. 3.4). That is, 68 percent of the grain-size values lie with
in plus or minus one standard deviation of the mean size. A formula for calculat
ing standard deviation by graphical-statistical methods is shown in Table 3.3.
Note that the standard deviation calculated by this formula is expressed in phi
( ) values and is called phi standard deviation. The symbol must a! ways be
Well Sorted (0.35 phi) Moderately Well Sorted (0.50 phi)
Visual images for estimating grain
size sorting. [After Harrell, j., 1984,
A visual comparator for degrees of
sorting in thin and plane sections:
jour.
Sed. Petrology, v. 54, Fig. 3,
4, 5, 6, p. 684, reproduced by per
mission of SEPM, Tulsa, Okla.]
Poorly Sorted (1.00 phi)
Verv Poorly Sorted (2.00 phi)
Mode,
Median,
Mean
Size
Decreasing Size
(Increasing Phi Values)
attached to the standard deviation value. Verbal terms for sorting corresponding
to various values of stdard deviation are as follows (after Folk, 1974):
Standard Deviation
<0.35
0.35-0.SO
0.50-0.7l
0.71-l.OO
1.00-2.¢
2.0-4.00
>4.00
very well sorted
well sorted
moderately well sorted
moderately sorted
poody sorted
very poorly sorted
extremely poorly sorted
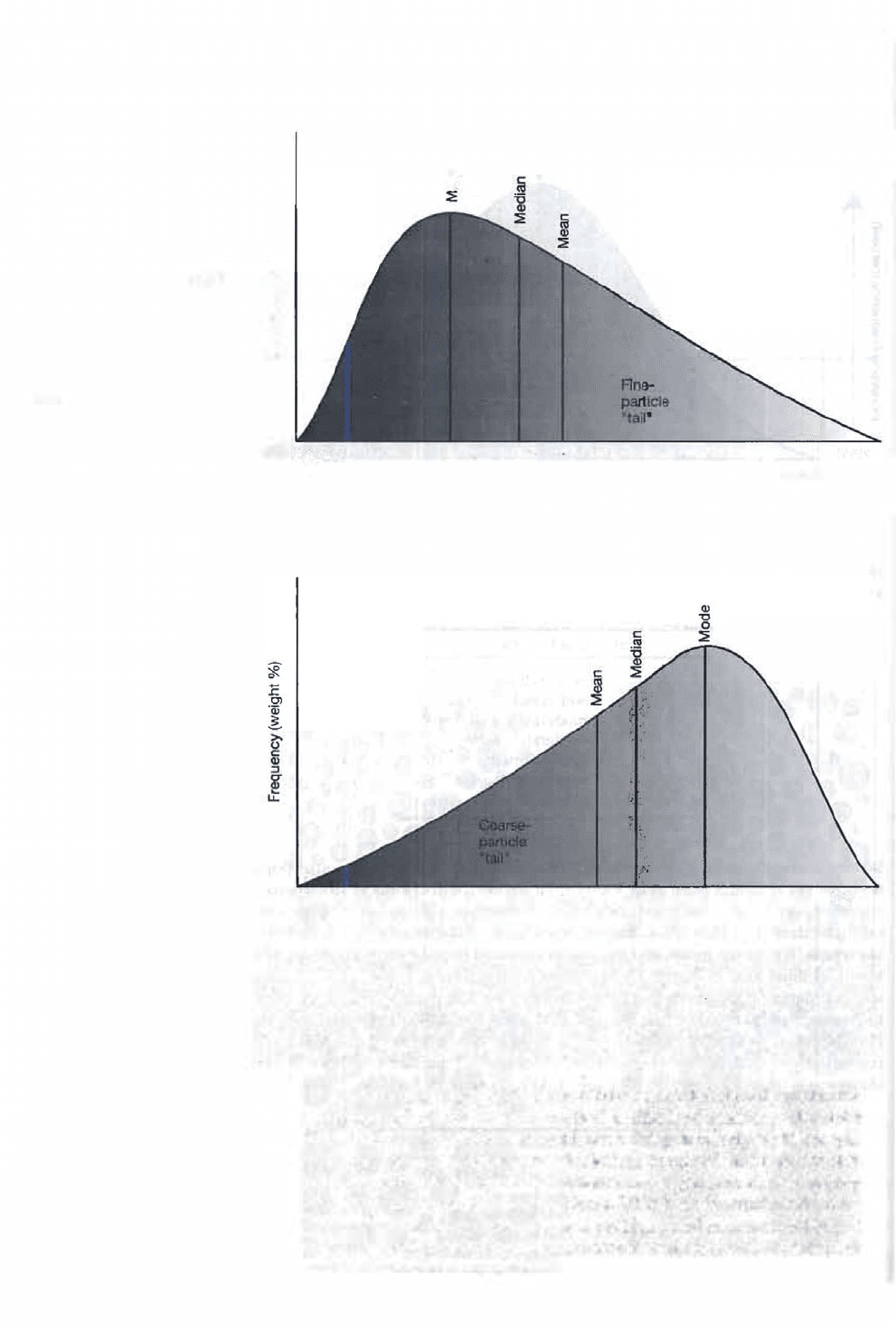
Skne and Kuosis. As mentioned, most natural sediment grain-size popula
o do not exhibit a normal or log-normal grain-size distribution. The frequency
cu of such nonnormal populations are not perfect bell-shaped curves, such as the
mple shown in Figure 3.4. Instead, they show some degree of asymmetry, or
skeess. The mode, me, and median in a skewed population of grai are all dif
fent, as iustrated in Figure 3.5. Skewness reflects sorting in the "tails" of a grain
se population. Populaons that have a tail of excess ne particles (Fig. 3.5A) are id
to be positiv�ly skewed or e skewed, that is, skewed toward positive phi values.
Populations with a of excess coarse particles (Fig. 3.5B) are negatively skewed or
se skewed. Graphic skewness can calculated by Equation 3 in Table 3.3. Verbal
skee is related to calculated values of skewness as follows (Folk, 1974):
>+0.30
+0.30 to +0.10
+0.10 to .10
-0.10 to .30
<-0.30
Skewness
strongly fine skewed
fine skewed
near symmetrical
coarse skewed
strongly coarse skewed
3.2 Grain Size
59
Figure 3.4
Grain-size frequency cue
for a normal distribution of
phi values, showing the rela
tionship of standard devia
tion to the mean, mode, and
median size. One standard
deviation ( la) on either side
of the mean size accounts for
68 percent of the area under
the frequency cue. [Based
in part on Friedman and
Sanders, 1978.]
60
Chapter 3 I Sedimentary Textures
A. Positively (fine) Skewed
0
�
�
:
"j
�
0
w
.
Coarse
Fine
Phi Size
B. Negatively (coarse) Skewed
Figure 3.5
Skewed grain-size frequency
curve, illustrating the difference
between positive (fine) and
negative (coarse) skewness.
Note the difference between
these skewed, asymmetrical
curves and the normal frequen
cy curve shown in Figure 3.4.
[Based in part on Friedman and
Sanders, 1 978.]
Coarse
Phi Size
Fine
Grain-size frequency curves can show various degrees of sharpness or
peakedness. The degree of peakedness is called kurtosis. A formula for calculat
ing kurtosis is shown in Ta ble 3.3. Although kurtosis is commonly calculated
along with other grain-size parameters, the geological significance of kurtosis is
unknown, and it appears to have little value in interpretative grain-size studies.
Moments. Grain size statistical parameters can be calculated diectly without ref
erence to graphical plots by the mathematkal method of moments (Krumbein
and Pettijo, 1938). The method had not en used extensively until compa ra
tively recently because of the laborious calculations invqlved and because if had
not been defitely proven that moment statistics are of greater value than graph
ical stastics application to geologic problems. With the advent of modem com
puters, lengthy calculations no longer pose a problem, and moment statistics are
now commonly used. The computations in moment statiscs involve multiplying
a weight (weight frequency in percent) by a distance (from the midpoint of each

n
Standard deviat ion
(d moment)
=
Skewness
f(m- )3
(3rd moment)
Sk
lOOa�
Kurtosis
f(m-
(4th moment)
K =
where
f
= weight percent (frequency)in each grain-size grade present
m
= midpoint of each grain-size grade in phi values
n
=
total number in sample; 100 when f is in percent
(
2
)
(
3)
(4)
size grade to the arbiary origin of the abscissa). Formulas for computing mo
ment
statistics are given in Table 3.4, and a sample computation form using 1/2
size classes is given in Table 3.5. Millimeter values can also be used in computing
moment statistics; that is, the size data need not be transformed to phi units. The
foulas shown in Table 3.3 can easily be programmed into a computer or pro
grammable calculator to calculate moment statistics from sieve data.
Application and Impoance of Grain-Size Data
Grain size is a fundamental physical property of sedimentary rocks and, as such,
is a useful descriptive property. Because grain size affects the related derived
properties of porosity and permeability, the grain size of potential reservoir rocks
is of considerable interest to petroleum geologists and hydrologists. For example,
coarse-grained, well-sorted sandstones are better reservoir rocks for oil than are
fine-grained, poorly sorted sandstones. Such well-sorted sandstones are also bet
aquifers for groundwater. Grain-size data are used in a variety of oer ways
(smarized by Syvitski, 1991):
1. To interpret coastal stratigraphy and sea-level fluctuations
2. To trace glacial sediment transport and the cycling of glacial sediments from
land to sea
3. By marine geochemists to understand the fluxes, cycles, budgets, sources, and
sinks of chemical elements in nature
4. To understand the mass physical (geotechnical) properties of seafloor sedi
ment, i.e., the degree to which these sediments are likely to undergo slumping,
sliding, or other deformation
Finally, because the size and sorting of sediment grains may reflect sedimentation
mechanisms and depositional conditions, grain-size data are assumed to be useful
for interpreting the depositial environments of ancient sedimentary rocks.
It is this assumption that grain-size characteristics reflect conditions of the
depositional environment that has sparked most of the interest in grain-size
alyses. Geologists have studied the grain-size properties of sediments and
dimentary rocks for more than a century; research eorts since the 1950s have
3.2 Grain Size
61

�
m
f
inteal
Midpoint
Weight
( )
()
%
Product
Deviation
squed
Product
cubed Product
quadrupled
Product
0.5
0.25
0.9
0.2
·2.13
4.54
4.09
-9.67
.70
20.60
18.54
0.5-1.0
0.75
2.9
2.2
-1.63
2.66
7.71
-4.34
-12.59
7.07
20.50
1.0-1.5
1.25
12.2
15.3
-1.13
1.28
15.62
-1.45
-17.69
1.63
19.89
1.2.0
1.75
13.7
24.0
�0.63
0.40
5.48
-.25
-3.43 0.16
2.19
2.0-2.5
2.25
23.7
53 3
-0.13
0.02 0.47
0.00
0.00
0.00
0.00
2.5-3.0
2.75
26.8
73.7
0.37
0.13
3.48
0.05
1.34
0.02
0.54
3.0-3.5
3.25
12.2
39.7
0.87
0.76
9.27
0.66 8.05
0.57
6.95
3.5.0
3.75
5.6
21.0
1.37
1.88
10.53
2.57
14.39
3.52
19.71
>4.0
4.25
2.0
8.5
1.87
3.50
7.00
6.55
13.10 12.25
24.50
Total
100.0
237.9
63.65
-5.53
112.82
Soue: McBride, E. , Mathematical treaent of si diStribution da. in R. E. Carver (cd.), Procedure.< in sedimentary petrolo.© 1971 by john Wiley & ns, Inc. Table 2, p. 119, repnted by permission of john
Wiley & s, Inc., New York.

focused particularly on statistical treatment of grain-size data. This prolonged pe
riod of grain-size research has generated hundreds of ]eaed papers in geological
jouals. Thus, it would be logical to assume that by now the relationship between
grai
n-size characteristics and depositional environments has been firmly estab
lished. Alas, that is not the case!
Many techniques for utilizing grain-size data to interpret depositional envi
ronm have been tried; however, little agreement exists regarding the reliability
of these methods. For example, Friedman (1967, 1979) used two-component grain
size variation diagrams, which one statistical parameter is plotted against an
other (e.g., skewness vs. standard deviation [sorting], or mean size vs. standard
deviation). This method putatively allows separation of the plots into major envi
roental fields such as beach environments and river environments (e.g., Fig.
3.6). Passega (1964, 1977) developed a graphical approach to interpreting grain
size data that makes use of what he calls C-M and L-M diagrams, in which grain
di ameter of the coarsest grains in the deposit (C) is plotted against either the me
dian grain diameter (M) or the percentile finer an 0.031 mm (L). Passega main
tains that most samples from a given environment will fall within a specific
environmental field in these diagrams. Visher (1969), Sagoe and Visher (1977}, and
Glaister and Nelson (1974) have all suggested that depositional environments can
interpreted on the basis of the shapes of grain-size cumulative curves plotted
on log probability paper. Cumulative curves plotted in this way commonly dis
play two or three straight-le segments rather than a single straight line (Fig. 3.7;
see Visher, 1969, for additional examples). Each segment of the curve is interpreted
to represent different subpopulations of grains that were transported simultane
ously but by different transport modes, that is , by suspension, saltation, and bed
load transport. Sediments from different environmen (dune, fluvial, beach, tidal,
nearshore, turbidite) can putatively be dierentiated on e basis of the general
sh apes of the curves, the slopes of the curve segments, and the positions of the
cation points (breaks in slope) between the straight-line segments (e.g., Visher,
1969). Although success using these various techniques has been reported by some
investigators, all of the techniques have been iticized for yielding incorrect results
an unacceptably high percentage of cases (e.g., Tucker and Va cher, 1980; Sedi
mentation Seminar, 1981; Vandenberghe, 1975; Reed, LeFever, and Moir, 1975),
More sophisticated multivariate statistical techniques, such as factor analysis
and discriminant function analysis (e.g., Chambers and Upchurch, 1979; Taira and
1.2
-
'
'
OA
'
o
\
\
-0.4
\
Mainly
c
river
j
-
\
sands
-1.2
-
Mainly
\
beach
I
sands
\
Figu 3.6
3.2 Grain Size
63
-2.0
-
-
-2,8
I
0
I
I
I
I
II
I I
0.4
0,8 1.2
Standard Deviation
I
Grain-size bivariate plot of moment skewness vs. moment standard de
viation showing the fields in which most beach and river sands plot.
[Redrawn from Friedman, G. M., 1967, Dynamic processes and statisti
cal parameters for size frequency distributions of beach and river sands:
]our. Sed. Petrology, v. 37, Fig. 5, p. 334, reproduced by permission of
SEPM, Tulsa, Okla.]

64
Chapter 3 I Sedimenta Textures
Figure 3.7
EXAMPLE SHOWING FOUR
TRUNCATED LOG NORMAL
POPULATIONS FROM LOWER
SWASH ZONE
SWASH-BACKWASH -
SEPARATION
WASH
LOAD
BREAK
SALTATION
POPULATION
SALTATION POPULATION
90
50
10
Relation of sediment transport dynam
ics to populations and truncation points
in a grain-size distribution as revealed
by plotting grain-size data as a cumula
tive curve on log probability paper.
[After Visher, G. 5., 1969, Grain size dis
tributions and depositional processes:
ZONE OF MI XING
Jour. Sed. Petrology, v. 39, Fig. 4, p.
1079, reprinted by permission of SEPM,
Tulsa, Okla.]
0
1
2
0.5
.250
3
4
PHI SCALE
.125 .067 MM SCALE
Scholle, 1979; Stokes, Nelson, and Healey, 1989) and the so-called log-hyperbolic
distribution (Bamdorff-Nielsen, 1977; Bagnold and Bamdor-Nielsen, 1980;
Bamdorff-Nielson et al., 1982), have also been used. These techniques have not yet
been widely applied, however, and some of the assumptions used in these statisti
cal methods have come under criticism (e.g., Forrest and Clark, 1989). Also, some
investigators (e.g., Fieller, Gilbertson, and Olbricht, 1984; Wyrwoll and Smith,
1985) report no better results with log-hyperbolic distributions than wh results
based on the normal probability function. Thus, it appears that after several
decades of intensive research to the techniques and significance of grain-size
analysis, during which the techniques for terpreting grain-size data have come
to demand creasingly sophisticated st atistical applications, there is little consen
sus as to their reliability for environmental analysis. Such is science!
Reasons why grain-size techniques for identifying depositional environments
of sediments fail to work consistently are probably related to variability in deposi
tional conditions within major environmental settings. e energy conditions and
sedimt supply with river systems, for example, can dier considerably from
one river to another and even within different parts of the same river system. Thus,
in some cases, the grain-size characteriscs of sediments may show as much vari
ability thin dferent parts of the same environmental setting as between differ
t environments. Grain-size disibutions reflect processes, not environments, and
sediment transport processes are not unique to a parcular environment. In any
case, grain-size data should be considered as oy one of the available tools for en
vironmental interpretation and should not be used alone for this purpose.
