Boggs S. Principles of Sedimentology and Stratigraphy
Подождите немного. Документ загружается.

2.2 Fundamentals of Fluid Flow
25
called the Reynolds number can be used to predict the boundary conditions sepa-
rating laminar and turbulent flow. Turbulent flow resists distortion to a much
greater degree than does laminar flow. Thus, a fluid undergoing turbulent flow
appears to have a higher viscosity than the same fluid dergoing laminar flow.
As mentioned, this apparent viscosity, which varies with the character of the tur-
bulence, is called eddy viscosity. Eddy viscosity results from turbulent momen-
tum, and it is the rate of exchange of fluid mass between adjacent water bodies. It
is necessary in dealing with uids undergoing turbulence to rewrite the equation
for shear stress to include a term for eddy viscosity. Thus, for laminar ow, shear
sess is given by the relation shown in Equation 2.1.1; however, for turbulent flow
the relationship becomes
d
u
T = (
+
)
d
y
(2.1)
where (eta) is eddy viscosity, which is commonly several orders of magnitude
higher than dynamic viscosity. For a more rigorous discussion of turbulence, see
Middleton and Wilcock (1994) and Williams (1996).
Reynolds Number
The fundamental differences in laminar and turbulent flow arise from the ratio of
inertial forces to viscous forces. Inertial forces, which are related to the scale and
velocity of uids in motion, tend to cause fluid turbulence. Viscous forces, which
crease with increasing viscosity of a fluid, resist deformation of a fluid and thus
tend to suppress turbulence. The relationship of inertial to viscous forces can be
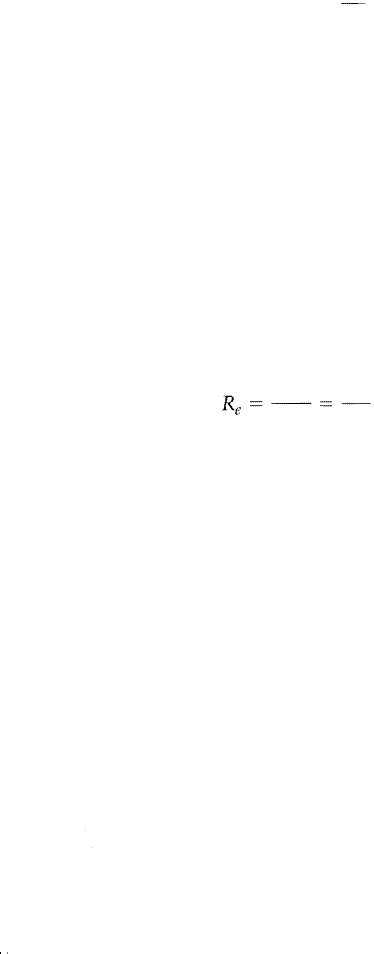
shown mathematically by a dimensionless value called the Reynolds number
(Re), which is expressed as
ULp
UL
v
(2.2)
where U is the mean velocity of flow, Lis some length (commonly water depth)
that characterizes the scale of ow, and v is kinematic viscosity. When viscous
forces dominate, as in highly concentrated mud flows, Reynolds numbers are
small and flow is laminar. Very low flow velocity or shallow depth also produces
low Reynolds numbers and laminar flow. When inertial forces dominate and flow
velocity increases, as in the aosphere and most flow in rivers, Reynolds num
bers are large and flow is turbulent. Thus, as mentioned, most ow under natural
conditions is turbulent. Note from Equation 2.2 that an crease in viscosity can
have the same effects as a decrease in flow velocity or flow depth. The transition
m laminar ow to turbulent flow takes place above a critical value of Reynolds
number, which commonly lies between 500 and 2000 and which depends upon
the boundary conditions such as channel depth and geometry. Thus, under a
g
iven set of boundary conditions, the Reynolds number can be used to predict
whether flow will be laminar or turbulent and to derive some idea of the magni
tude of turbulence. Because the Reynolds number is dimensionless, it is of partic
ular value when used to compare scaled-down models of flow systems with
natural flow systems, as in modeling natural systems.
Boundary Layers and Ve locity Profiles
When a fluid flows over a solid surface (boundary) such as a streambed, flow in
e immediate vicity of the boundary is retarded by the frictional resistance of
e boundary. This zone of retardation is called a boundary layer. The boundary
layer is the region of fluid flow next to the boundary across which the fluid velocity

26
Chapter 2 I Tr ansport and Deposition of Siliciclastic Sediment
grades from that of the boundary (commonly zero) to that of the unafcted part of
the ow (see velocity proles in Fig. 2.1). Boundary layers may be comparavely thin
or they may extend all the way to the e surface of a flow. Also, flow within bound
ary layers may be laminar or turbulent or may grade from laminar to turbulent.
Because of the greater shear stress required to maintain a particular velocity
gradient in turbulent flow, turbulent ow-velocity profiles, both vertically in the
flow and horizontally across the ow, have different shapes than do laminar ow
velocity profiles (Fig. 2.1). Owing to variations in flow velocity during tbulent
flow, the shape of the turbulent-flow vertical profile is determined by time-averaged
values of velity. Under conditions of turbulent flow, laminar or near-laminar flow
occurs only very near the bed. The exact shape of the turbulent profile depends
upon the nature of the bed over which the flow takes place. For smooth beds,
there is a thin layer close to the bed boundary where molecular viscous forces
dominate. Molecular adhesion causes the uid immediately at the boundary to
remain stationary. Successive overlying layers of uid slide relative to those be
neath at a rate dependent upon the fluid viscosity. Flow within this thin layer
tends toward laminar, although it is characterized by streaks of faster and slower
moving fluid and is not truly laminar. This layer is the viscous sublayer, or lam
inar sublayer.
If sediment particles on a streambed are so small (mud to fine-sand size) that
they lie within the viscous sublayer, the near-bed ow is dominated by viscous
forces and the flow is said to be hydraulically smooth. If the grains are so large
that they exceed the thickness of the viscous sublayer and thus protrude into the
turbulent part of the ow, the flow is hydraulically rough. Over a very rough or
irregular bed such as coarse sand or gravel, the viscous sublayer is destroyed by
these irregularities, which extend through the layer into the turbulent flow. The
ow
of uid over a boundary is thus affected by the roughness of the boundary.
Obstacles on the bed generate eddies at the boundary of a ow; the larger and
more abundant the obstacles, the more turbulence is generated.
Most sediment transport takes place within boundary layers; turbulent
boundary flow is much more effective in erodg and transporting sediment than
is laminar ow. The presence or absence of a viscous sublayer may be an impor
tant factor in initiating grain movement. That is, extremely small gras that lie en
tirely within the viscous sub layer may difficult to move.
Box 2.2 Boundary (Bed) Shear Stress
As a fluid flows across i bed, a stress that opposes the motion of the fluid ex
ists at the bed surface. This stress, called the boundary shear stress (To) to dif
ferentiate it from fluid shear stress ( T ), is defined as force per unit area parallel
to the bed, at is, the tangential force per unit area of surface (the mean shear
stress acting over the wetted perimeter). It is a function of the density of the
uid, slope of the bed, and water depth. Boundary shear stress is expressed
(Allen, 1994) as
To ypghs
(2.2.1)
where y is density of the fluid, pis uid density, g is gravitational acceleration,
h
is ow depth, and s is the slope of the parallel bed and water surface (gradi
ent). The boundary shear stress is also a nction of velocity of ow, a complex
mathematical relationship not shown here. It tends to increase as velocity in
creases, alough not in a direct way. e bed shear stress increases linearly
with dep and slope.
Because boundary shear stress is deteined by the force that a flow is able
to exert on e sediment bed and is related to flow velocity, it is an important

2.3 Particle Tra nsport by Fluids
27
variable in determing the erosion and transport of sediment on the bed below a
flow. Equation 2.2.1 indicates that bounda shear sess increases ectly with
increasing density of the moving fluid, increasing diameter and depth of the
stream channel, and increasing slope of the streambed. Other fa ctors being equal,
we would thus expect to see greater unda shear strs, and greater ability to erode and
transport sediment, in water ows than in air ows, in larger stream channels than in
smaller channels, and in high-gradient streams than in low-gradient streams.
Froude Number
addition to the effects of fluid viscosi and inertial forces, gravity also plays a
role in fluid flow because gravity influences the way in which a fluid transmits
surface waves. The velocity with wch small gravity waves move in shallow
water
is given by the expression , in which g is gravitational acceleration and
L water depth. The ratio between inertial and gravity forces is the Froude num
ber (F,), which is expressed as
F,
u
(2.3)
where U is again e mean velocity of ow and L is water depth, in the case of
water flowing in an open channel. The Froude number, like the Reynolds number,
a dimensionless value and thus is very useful in modeling studies.
When the Froude number is less an 1, the velocity at which waves move is
greater than flow velocity, and waves can travel upstream. That is, waves in a
stream move upstream in the direction opposite to current flow. For example, if
you threw a stone to a slow-moving stream having a Froude number less than 1,
waves created by impact of the stone could spread upstream. Flow under these
conditions is called tranquil, streaming, or subcritical. If the Froude number is
greater than 1, waves cannot be propagated upstream, and flow is said to be rapid,
shooting, or supercritical. Thus, the Froude number can be used to defe the crit
ical velocity of moving water at which ow at a given depth changes from tran
quil to rapid (such as change from tranquil ow in a stream channel wi a gentle
slope to rapid flow where the chael becomes steeper) or vice versa. The Froude
number also has a relationship to flow regimes, which are defined by characteris
tic bedforms, such as ripples, that develop during fluid flow over a sediment bed.
This relationship is discussed further in Chapter 4.
2.3 PA RTICLE TRANSPORT BY FLUIDS
Having established some of the fundamentals of fluid behavior during flow of flu
ids alone, we are now at a point where we can consider the more compcated
processes of transport of sediment by uid ow. Transport of sediment by fluid
flow involves two fundamental steps: (1) erosion and entrainment of sediment
om the bed and (2) subsequent, sustained downcurrent or downwind move
mt of sediment along or above the bed. The term entrainment refers to the
processes involved in lifting resting grains from the bed or otherwise putting
them into motion. More energy is commonly required to initiate particle move
ment than to keep particles in motion after entrainment. Thus, a great deal of ex
perimental and theoretical work has been directed toward study of the conditions
necessary for particle entrainment. Once particles are lifted from the sediment bed
into the overlying water or air column, the rate at which they fall back to e bed
(the settlg velocity) is an important factor in determining how far the particles

28
Chapter 2 I Transport and Deposition of Siliciclastic Sediment
travel downcurrent before they again come to rest on the sediment bed. Like par
ticle entrainment, the settling velocity of particles has been studied extensively.
We will now examine some of these fundamental aspects of particle transport by
fluids, beginning with a look at the factors involved in entrainment of sediments
by a moving body of fluid.
Paicle Entrainment by Currents
As the velocity and shear stress of a fluid moving over a sediment bed increase, a
critical point is reached at which grains begin to move downcurrent. Ty pically, the
smaller and lighter grains move first. As shear stress increases, larger grains are
put into motion until finally grain motion is common everywhere on the bed. This
critical threshold for grain movement is a direct function of several variables, in
cluding the boundary shear stress, fluid viscosity, and particle size, shape, and
density. Indirectly, it is also a function of the velocity of flow, which varies as the
logarithm of the distance above the bottom.
To understand the problems involved in lifting particles from the bed and
initiating motion, let us consider the opposing forces that come into play as a fluid
moves across its bed. As shown in Figure 2.2A, forces caused by gravity act down
ward to resist motion and hold particles against the bed. The gravity forces result
from the mass of the particles and are aided in resisting grain movement by fric
tional resistance between particles. Fine, clay-size particles have added resistance
to movement owing to cohesiveness that arises from electrochemical bonds be
tween these small grains. The motive forces that must be generated by fluid flow
to overcome the resistance to movement imposed by these retarding factors in
clude a drag force, which acts parallel to the bed and is related to the boundary
shear stress, and a lift force caused by the Bernoulli effect of fluid flow over
projecting grains. The drag force (F0) depends upon the boundary shear stress
A
Lift
Gravity Force
FG
Figure 2.2
I
pivot
STREAMLiNES AND PRESSURE FORCE VECTORS
(a)
VELOCITY VECTORS
(b)
A. Forces acting during fluid flow on a grain resting on a bed of similar grains. B. Flow
pattern of fluid moving over a grain, illustrating the lift forces generated owing to the
Bernoulli effect: (a) streamlines and the relative magnitude of pressure acting on the sur
face of the grain. (b) direction and relative velocity of velocity vectors; higher velocities
occur where streamlines are closer together. [A., after Middleton, G. V., and j. B. Southard,
1978, Mechanisms of sediment movement: Eastern Section, Soc. Econ. Paleontologists
and Mineralogists Short Course No. 3, Fig. 6.1, p. 6., reprinted by permisssion of SEPM,
Tulsa, Okla. B. Streamlines and velocity vectors, from Blatt, H., G. V. Middleton, and
R. Murray, 1980, Origin of sedimentary rocks, 2nd ed., Fig. 4.9, p. 107, reprinted by
permission of Prentice-Hall, Englewood Cliffs, N.j.]
2.3 Paicle Transport by Fluids
29
(r0} and the drag exerted on each grain exposed to this stress. The hydraulic lift
force (} known as the Beoulli effect is caused by the convergence of fluid
stamlines over a projecting grain. The Bernoulli effect results from an increase
flow velocity in the zone where the streamlines converge over the grain. This ve-
locity increase causes pressure to decrease above the grain. Hydrostatic pressure
om below then tends to push the grain up off the bed into is low-pressure zone
(Fig. 2.2B) for e same reason that lift is created when air flows over the curved
wing of an airple. The drag and lift forces combine to produce the total fluid
force, represented by the fluid-force vector (FF) in Figure 2.2A. For grain move-
ment to occur, the fluid force must be large enough to overcome the gravity and
ictional forces.
The preceding discussion is greatly simplified and generalized, and anum
ber of factors complicate caulation of crical thresholds of grain movement
under
natural conditions. These factors clude variations in shape, size, and sort
ing of grains; bed roughness, which controls the presence or absence of a viscous
sublayer; and cohesion of small particles. Because of these complicatg factors,
e critical conditions for particle entrainment cannot be calculated and must be
determined experimentally. The simplest plot that shows an experimentally de
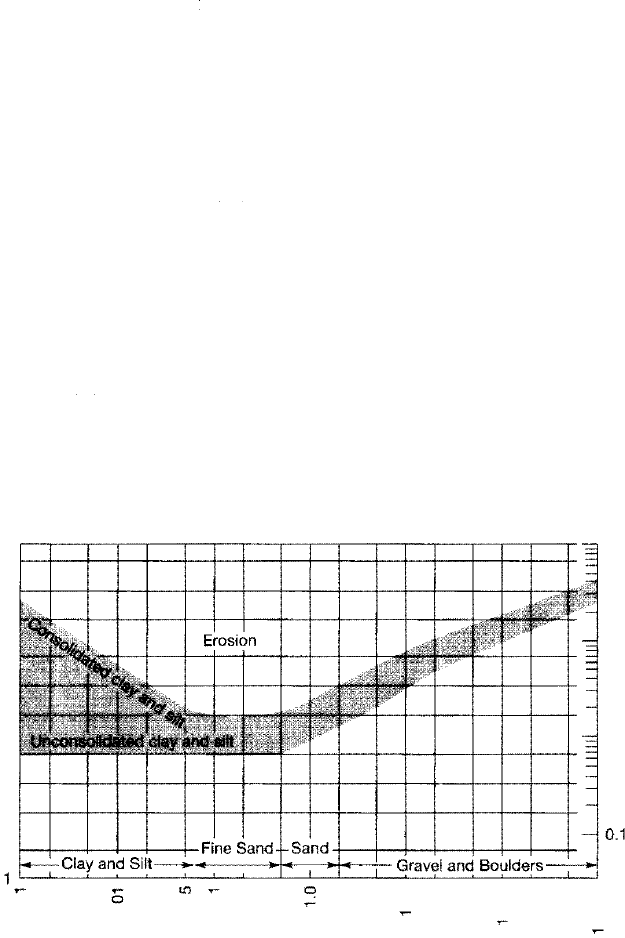
rived threshold graph for initiation of gra movement is the Hjulsom diagram.
In the Hjulstrom diagram (Fig. 2.3), the velocity at which grain movement
begins as ow velocity increases above the bed is plotted against mean grain size
(grain diameter). This diagram shows the critical velocity for movement of quartz
grains on a plane bed at a water depth of 1 m. The curve separates the graph into
two fields. Points above the graph indicate the conditions under which grains are
in motion, and points below indicate no motion. Note from this figure that critical
entrainment velocity for grains larger than about 0.5 mm increases gradually with
incasing mean grain size, whereas the entrainment velocity for consolidated
100.0
2000
1000
500
10.0
0
200
l
E
100
50
0
20
�
�
E
1.0
0
0
�
10
5
2
�
0
�
0
0 0 0
0
0 0 0 0
0
8
0 0 0
0
0
N
0 0
0 0
0
Grain size (mm)
2.3
The Hjulstrom diagram, as modified from Sundberg, showing the critical current velocity
required to move quartz grains on a plane bed at a water depth of 1 m. The shaded area
indicates the scatter of experimental data, and the increased width of this area in the finer
grain sizes shows the effect of sediment cohesion and consolidation on the critical velocity
required for sediment entrainment. [After Sundborg, A., 1956, The River Klarlven, a study
of fluvial processes: Geografiska Annaler, Ser A., v. 38, p. 197, reprinted by permission.]

30
Chapter 2 I Transport and Deposition of Siliciclastic Sediment
clay and silt grains smaller than 0.05 mm increases with decreasing grain size.
is seemingly anomalous behavior at smaller grain sizes is apparently due main
ly to increasing cohesion of ner size particles, making them more difficult to
erode than larger, noncohesive particles. Also, extremely small grains may lie
within the viscous sublayer, where little grain movement takes place.
Box 2.3 The Shields Diagram
The Hjulstrm diagram is somewhat limited in its application because it is sict
ly
valid only at a water depth of 1 m on a plane bed d only in water in which
fluid and grain densities and dynamic viscity are constant, as in freshwater
seams in a given season during average flow. The Shields diagram (Fig. 2.3.1) is
also a threshold aph for initiation of sediment grain movement that is widely
used by sedimentologists and is well established by experimental work. It has
more rigor than the Hjulstrom diagram and it has a more general applicaon.
For example, it can be used for wind as well as water and for a variety of con
ditions
in water. It is, however, more complex and difficult to understand than
is the Hjulstrom diagram because it involves two dimensionless relationships.
In Figure 2.3.1, dimensionless shear stress (,_) (called by some workers) is
used instead of flow velocity as a measure of ctical shear, and the mean grain
size parameter used in the Hjulstrom diagram is replaced by the grain
Reynolds number (Reg), another dimensionless quantity. The dimensionless
bed shear stress ( 01) is given by
(2.3.1)
where Tt is boundary shear stress, Ps is density of the parcles, p is density of
the uid, g is gravitational acceleration, and Dis particle diameter. The value of
dimensionless shear stress increases with increasing bed shear stress and in
creasing velocity; it decreases with increasing density and size of the particles.
Instead of velocity in Hjulstrom's diagram, the dimensionless shear stress thus
incorporates shear stress (velocity), grain size, and grain and fluid densities
into a single term, which plotted on the vertical axis of Shields' diagram. An
increase in dimensionless shear stress indicates either an increase in tlow veloc
ity and shear stress or a decrease in grain size or grain density.
10
°
0.6
0.4
,q
0.2
'
;
10�1
I'
06
�
04
02
10 2
Figure 2.3.1
Shields (1936)
10�1
R' u·o
v
Miller et al.
1977
\
The Shields diagram as modified by Miller. (After Miller, M.C., et al., 1977, Threshold
of sediment motion under unidirectional currents: Sedimentology v. 24, Fig. 2, p. 51 1,
reproduced by permission.)

2.3 Particle Transport by Fluids
31
e grain Reynolds number (
R
e
g
) differs from the ordinary Reynolds
number previously discussed. The length or water depth value (L) of the ordi
na Reynolds number is replaced by particle diameter (d) and the ow veloci
ty (U) by shear velocity (U*). The grain Reynolds number is a measure of
turbulence at the gra-fluid boundary. It is thus expressed as
U*d
R
e
g
=
v
(2.3.2)
The grain Reynolds number, plotted on the horizontal axis of Shields' diagram,
is clearly not the same tng as mean grain size; however, it can be seen from
Fi gure 2.3.1 that the grain Reynolds number increases with increasing grain
size if shear velocity and kinematic viscosity remain constant. Thus, an increase
in grain Reynolds number means an increase in grain size, an increase in shear
velity and turbulence, or a decrease in kinematic viscosity.
The Shields diagram is less intuitive than Hjulstrom's diagram in which
fluid velocity is plotted against grain size; however, points above the curve in
dicate that noncohesive grains on the bed are fully in motion and points below
indicate no motion, as in the Hjulstrom diagram. Beginning of motion is deter
mined by the dimensionless shear stress, which increases with increasing bed
sar stress under a given set of conditions for gra density, uid density, and
grain size. The critical dimensionless shear stress required to initiate grain
movement thus depends upon the gra Reynolds number, whi in turn is a
nction of grain size, kinematic viscosity, and turbulence. Note from the
Shields diagram in Figure 2.3.1 that the dimensionless bed shear stress increas
es
slightly vvh increasing grain
Reynolds number above about 5 to 10, al
though it remains maly between 0.03 and 0.05. At lower Reynolds numbers,
the value increases steadily up to a value of 0.1 or higher. This greater rate of in
crease
at lower Reynolds numbers is related to the presence of the viscous sub
layer. hen the bed is composed of small particles on the order of fine sand or
smaller, a smooth boundary and hydraulically smooth ow result; the particles
lie entirely within the viscous sublayer, where flow is essentially nonturbulent
and instantaneous velocity variations are less than in the lower part of the over
lying turbulent boundary layer. For coarser particles, the viscous sublayer is so
in that the grains project through the layer into the turbulent ow.
Several complicating factors not covered in the Hjulstrom and Shields dia
grams make prediction of the onset of grain movement difficult. Itantaneous
fluctuations in boundary shear stress may ase from local eddies or from wave ac
tion superimposed on current flow, and these fluctuations may cause some parti
cles to move before e general onset of grain movement. Fine muds and silts may
not erode to yield individ ual grains owing to the tendency of such cohesive mate
rials to be removed as chunks or aggregates of grains.
Many of the processes volved in sediment entrainment and transport can be
eecvely modeled by computer simulation. excellent book on this subject,
Simulating Clastic Sedimentation (Tetzlaff and Harbaugh, 1989), takes the ader throu
e computations and reasoning of erosion, ansportaon, and deposition of clasc
sediment. The book furer provides detailed insuctions on the teciques and
computer programs used to simulate clastic sedimtation. For further insight into
simulang sediment transport, see Slingerland, Harbaugh, and Furlong (1994).
Role of Paicle Settling Velocity in ansport
As soon as grains are lifted above the bed during the entrainment process, they
begin to fall back to the bed. The distance that they travel downcurrent before
again coming to rest on the bed depends upon the drag and lift forces exerted by

32
Chapter 2 I Transport and Deposition of Siliciclastic Sediment
the current, including turbulence, and the settling velocity of the particles. A par
ticle initially accelerates as it falls through a fluid, but acceleration gradually de
creases until a steady rate of fall, called the teinal fall velocity, is achieved. For
small particles, terminal fall velocity is reached very quickly. The rate at which
particles settle after reaching fall velocity is a function of the viscosity of the fluid
and the size, shape, and density of the particles. The settling rate is determined by
the interaction of upwardly directed forces-owing to buoyancy of the fluid and
viscous resistance (drag) to fall of the particles through the fluid-and down
wardly directed forces arising from gravity. The drag force exerted by the fluid on
a falling spherical grain is proportional to the density of the fluid (Pr ), the diame
ter (d) of the grains, and the fall velocity (V), as given by the relatio'ship
Drag force =
(2.4)
where Co is a drag coefficient that depends upon the grain Reynolds number and
e parcle shape. The upward force resulting from buoyancy of the uid given by
(2.5}
where P
f
is fluid density and g is gravitational acceleration. [Note: 4/3
7
T(d/2)3 is
the volume of a sphere.] The downward force owing to gravity is given by
4 (d)3
Fx = 3
7
T 2
p
(2.6)
where Ps is particle density.
As the particle stops accelerating and achieves
fall
velocity, the drag force of the liquid on the falling particle is equal to the down
ward force due to gravity minus the upward force resulting from buoyancy of the
liquid. Thus
(2.7)
Rearranging terms, we can explain this relationship in terms of fall velocity ( as
2
4gd
(
p
,-
v = ---
3C
o
P
f
(2.8)
For slow laminar flow at low concentrations of particles and low grain Reynolds
numbers (Re
x
' see Box 2.3), C0 has been determined to equal 24/ Re
g
(Rouse and
Howe, 1953, p. 182}. Substituting this value (24/U'd/ I P
f
) for Co yields
1 (
P
s
P
t
)gd2
V=--...
.
_
18
(2.9)
which is Stokes's Law of settling, with particle size expressed as diameter in cen
timeters. This law, formulated by Stokes in 1845, is often simplified to
V
= CD2 (incm/sec)
(2.10)
where C is a constant equaling
(
p
5-
p
f
}g /18 and D is the diameter of particles
(spheres) expressed in centimeters. Values of C have been calculated for a range of
common laboratory temperatures (e.g., Galehouse, 1971); thus, seting velocity
( can be determined quickly for any value of particle diameter (D). Note that the

2.3 Particle Transport by Fluids
33
Reynolds number is a distinguishing factor in grain settling behavior just as it is
laminar and turbulent flow.
Experimental determination of particle fall velocity shows that Stokes's Law
accurately predicts settling velocity of particles in water only for particles less
than about 0.1 to 0.2 mm in diameter. Larger particles have fall velocities lower
than those predicted by Stokes's Law, apparently owing to inertial (turbulent) ef
fec ts caused by the increased rates of fall of these larger grains. Thus, the Stokes
equation cannot be used for determining the settling velocity of sand, a very im
portant component of most sediment. The fall velocity is also decreased by de
case in temperature (which ncreases viscosity), decrease in particle density, and
decrease in the sphericity (the degree to which the shape of a particle approaches
the shape of a sphere of the particles. Most natural particles are not spheres, and
departure from spherical shape decreases fall velocity. Fall velocity is also de
creased by increasing concentration of suspended sediment in the fluid, which in
€reases the apparent viscosity and density of the fluid, and by turbulence.
ediment Loads and Transport Paths
Once sediment has been eroded and put into motion, the transport path that it
takes during further sustained downcurrent movement is a function of the settling
velocity of the particle and the magnitude of the current velocity and turbulence.
Under a given set of conditions, the sediment load may consist entirely of very
coarse particles, entirely of very fine particles, or of mixtures of coarse and fine
particles. Coarse sediment such as sand and gravel moves on or very close to the
bed
during transport and is considered to constitute the bed load (Fig. 2.4). Finer
material
carried higher up in the main flow above the bed makes up the
sus
p
ended load. If the shear velocity (U*) is greater than the settling velocity (,
material will remain in suspension.
Bed Load Tr ansport
Pa rticles larger than sand size are commonly transported as part of the bed load in
essentially continuous contact with the bed. This type of transport, called traction
transport, may include rolling of large or elongated grains, sliding of grains over
or past each other, and creep. Creep results from grains being pushed a short dis
tance along the bed in a downcurrent direction owing to impact of other moving
grains. Saltation is a type of bedload transport in which grains, particularly sand
size grains, tend to move in intermittent contact with the bed. Saltating grains
move by a series of jumps or hops, rising off the bed at a steep angle ( �45°) to a
height of a few grain diameters and then falling back along a shallow descent path
of about 10°. This asymmetric saltation path may be interrupted by turbulence or
t
it
t
t 8U
�
Col
lisi
o
n
eve
�
·
�
r
ntins
�
i
o
n
.
�
Figure 2.4
Schematic illustration of
grain paths during bedload,
suspension, and saltation
transport. [Based in part on
Leeder, M. R., 1979, Bed
load dynamics: Grain inter
actions in water flows: Earth
surface processes, v. 4,
Fig. 5, p. 237, john Wiley
& Sons.]
34
Chapter 2 I Transport and Deposition of Siliciclastic Sediment
by collision with another grain (Fig. 2.4). Saltation transport may be thought of as
intermediate between traction transport and suspension transport, but it is de
scribed here as part of bedload transport because most saltang grains remain rel
atively dose to the bed during movement.
Suspended Load Tr ansport
As the flow strength of a current increases, the intensity of turbulence increases
dose to the bed. Particle trajectories become longer, more irregular, and higher up
from the bed than the trajectories of saltating grains. Upward components of fluid
motion resulting from turbulence increase to the point that they balance down
ward gravitational forces on the particles, allowing the particles to stay suspended
above the bed far longer than could be predicted from their settling velocities in
nonturbulent water. If the lift forces arising from turbulence are erratic and do not
continuously maintain this balance, a common occurrence during transport of
fine-to-medium sand, the grains may drop back from time to time onto the bed.
This behavior is called intermittent suspension (Fig. 2.4). Intermittent suspension
differs from saltation because the suspended particles tend to be carried higher
above the bed and remain off the bed for longer periods of time. Smaller particles
have settling velocities that may be so low that they remain in nearly continuous
suspension and are carried along at almost the same velocity as the fluid flow.
Wash Load
Much of the sediment load undergoing continuous suspension transport is com
posed of fine, day-size particles with very low settling velocities. In rivers, ts
sediment is derived either from upstream source areas or by erosion of the bank,
rather than from the streambed, and is called the wash load. Rivers have the
capacity to ansport large wash loads even at very low velocities of flow. Because
the wash load travels in continuous suspension at about the same velocity as the
water, it is transported rapidly through river systems.
anspo by Wind
Wind can be considered a very low density, low viscosity "fluid" that is capable of
flowing and bringing about sediment transport. The principles involved in en
trainment and transport of particles by wind (eolian transport) are similar to those
for water; however, wind's low density and viscosity cause the threshold values for
wind entrainment and transport to be quite different (see discussion by Nickling,
1994). Entrainment of grains by wind action can be strongly aected by the impact
of moving grains hitting the bed. At a value of wind velocity below the critical ve
locity needed to initiate grain movement, grain motion can be started and propa
gated downwind by throwing grains onto the bed, a process referred to as seeding.
This lower threshold for grain movement is called the impact threshold.
Wind commonly transports parcles of fine-sand size and smaller only.
Sand-size particles move by traction (surface creep) and saltaon and dust-size
particles by suspension. Transport takes place at relatively high wind velocities,
and
the flow is commonly turbulent, characterized by eddies of various sizes
moving with different speeds and directions. Suspended loads carried by the
wind are called dustloads. Upward diffusion in unstable, buoyant air masses at an
advancing ont have been known to carry dust douds rapidly to heights of hun
dreds or even thousands of meters during volcanic eruptions. Material carried to
such great heights may remain in suspension for long periods of time and subse
quently be spread over a very broad area, including the ocean basins (Prospe,
1981). In fact, the very fine grained component of deep-sea pelagic sediments is
believed to be largely of windblown origin.
