Boggs S. Principles of Sedimentology and Stratigraphy
Подождите немного. Документ загружается.


2.4 Particle Transport by Sediment Gravity Flows
45
is similar to liquefied flow many respects and may, in fact, grade into these
ows . conast to liquefied ows, grain flow can occur under subaerial condi-
tions as well as subaqueous conditions.
Grain flow is common on the lee slopes of sand dunes. Flows of cohesionless
sd have also been observed and photographed in the ocean as they moved
down steep slopes in submarine canyons (Shepard, 1961; Dill, 1966; Shepard and
Dill, 1966). Gra flows over e floors of Norwegian ords are reported to be
sponsible for breaking submarine telephone cables. Grain flows may be of limited
geolcal significance because of the steep slopes required to initiate flow, al
ough it has been suggested at grain flow may accompany turbidity currents
on less steep slopes, moving beneath but independently of the turbidity currents.
position of grain-flow sediment occurs quickly and en masse by sudden " freez
g," primarily as a result of reduction of slope angle.
Grain-Flow Deposits
Grain-ow origin has been suggested by some workers for very ick, almost
massive sandstone beds; however, Lowe (1976) concluded that the deposits of a
single
gra flow in any environment cannot be icker than a few cenmeters for
sand-size grains. Reverse grading (that is, grading from fine size to coarse size
upward, which occurs some sandstones) has been attributed to grain-ow
pcses. Reverse grading is assumed to form during grain flow as a result of
aller particles filtering down through larger particles while they are in the dis
d state, a process called kinetic sieving.
Grain-flow deposits are massively bedded with little or no ternal lamina
and grading except possible reverse grading in the base (Fig. 2.7C). Deposits
of
a single grain ow are commonly less than about 5 em thick
bris Rows and Mud Rows
Subaerial debs flows occur under many cmatic conditions but are particularly
common in arid and semiarid gions where they are usually initiated after heavy
rainfalls. They are also common volcanic regions where volcanic debris become
water saturated during heavy rains that accompany eruptions or from melting ice
d snow that accumulate on volcanic cones between eruptions. Debris flows are
slur ke flows composed of highly concentrated, poorly sorted mixtures of sedi
ment and water that behave in a different manner than fluid flows.
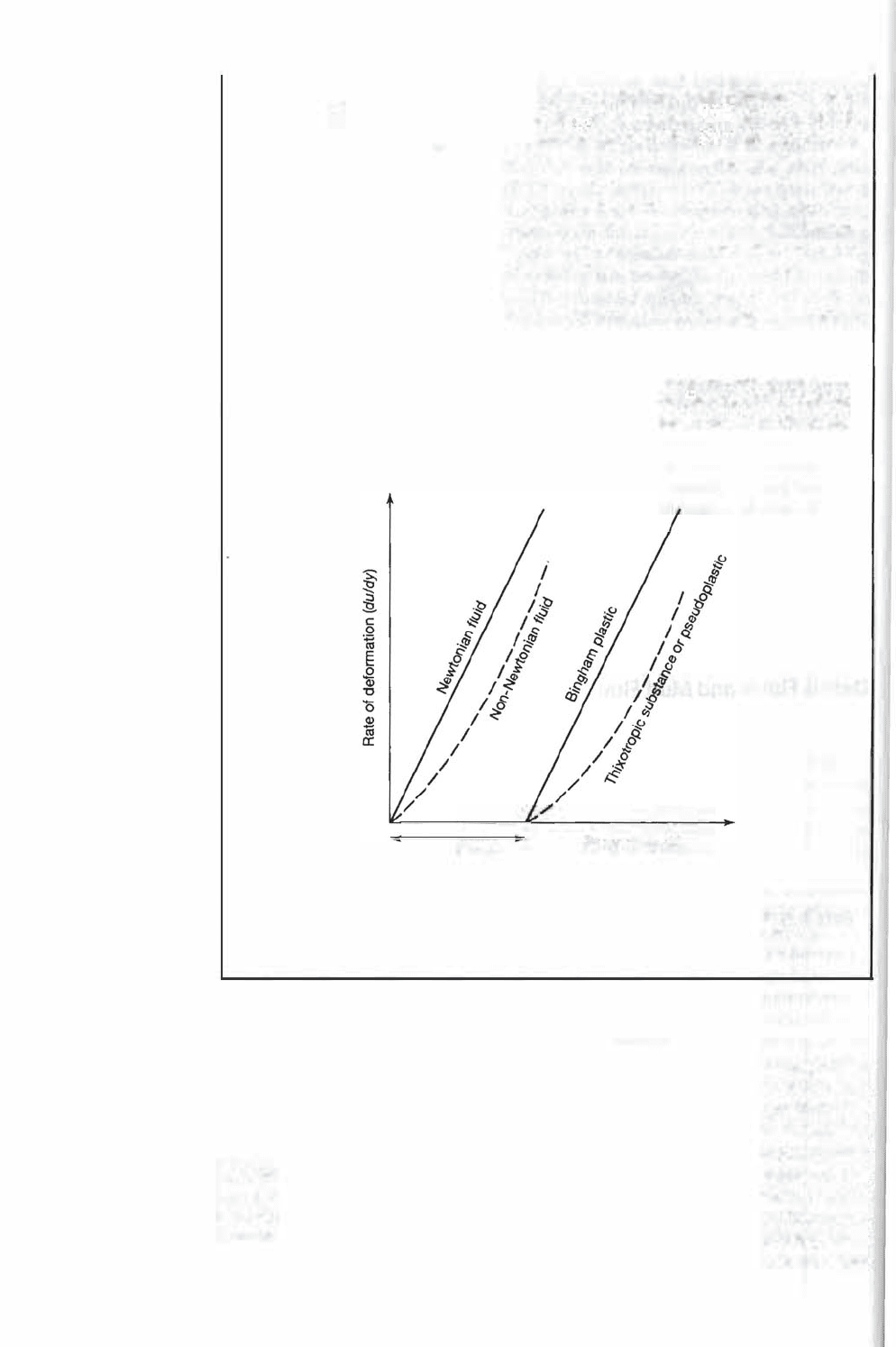
Box 2.5 pes of Fluids
pding upon the extent to which dynamic viscosity () changes with
shear or strain (deformation) rate, three general types of uids can be defined.
Ntian uids have no strength and do not undergo a change viscosity
e shear rate increases (Fig. 2.5.1). Thus, ordinary water, which does not
cnge viscosity as it is stred or agitated, is a Newtonian fluid. Non-Newtonian
fluids have no strength but show variable viscosity () with change in shear
or sain rate. Water that contains dispersions of sand in concentrations greater
about 30 percent by volume, or even lower concentrations of cohesive
cy, behaves as a non-Newtonian uid. Therefore, highly water-saturated,
c opacted muds may display non-Newtonian behavior. Such muds may
ow sluishly at low flow velocities but display less viscous flow at higher
velocities.
me extremely concentrated dispersions of sement may behave as
plasc substances, which have an initial strength that must be overcome before
46 Chapter 2 I Transport and Depositi
o
n of Siliciclastic Sediment
they yield. If the plasc material behaves a a substance with constant viscosi
ty after the yield stngth is exceeded, it is called a �ingh plastic. Obris
flows which large cobbles or boulders are supported a matix of tersti·
tial fluid and fine sediment are examples of natural substances that behave as
Bingham plastics. Water with dispersed sediment, and other plastic materi
als (such as ice), which behave as substances with variable viscosi after
yield strength is exceeded and they start to flow, are called pseudoplastics.
ixotropic substances, a special type of pseudoplastic, have stngth until
sheared. Shearing destroys their strength; the substances then behave like a
fluid (commonly non-Newtonian) until allowed to st a short while, after
which strength is regained. Freshly deposited muds commonly display
thotropic behavior. Shearing resulting from earthquake tremors, for exam
ple, can cause liquefaction and failure of such muds. Such momentary lique
faction may result in downslope movement of sediment that otherwise would
not dergo transport. Differences in behavior of Newtonian fluids, non-New
tonian fluids, and plastic substances in response to shear strs are illushated
schematically Figure 2.5.1.
Yleld stress
Shear stress (T)
Fire 2.5.1
Types of fluids: rates of deformation vs. shear stress for fluids and plastics. [After Blatt,
H., G. V. Middleton, and R. Murray, 1980, Origin of sedimenta rocks, 2nd ed., Fig.
5.26, p. 187. Reprinted by permission of Prentice-Hall, Englewood Cliffs, N.j.]
Debs-Flow Mechanisms
Debris flows behave as Bingham plastics; that is, they have a yield strength that
must be overcome before flow begins. The cohesive mud matrix debris flows
has enough strength to support large grains, but cohesiveness is not great enough
to prevent flow on an adequate slope. Debris flows are generally iniated on steep
slopes ( > 10°), but they can flow considerable distances on gentle slopes of 5° or
less; they occur both subaerial and subaqueous environments. They consist of
poorly sorted mixtures of particles, which may range to boulder-size, a fine
gravel, sand, or mud matrix. Those composed predominantly of mud-size grains
are mud flows and those with a lower but substantial mud fraction (>5 percent
by volume) are muddy debris flows (Middleton, 1991). The grains these

Further Reading
47
mud-bearing debris flows are supported in a matrix of mud and interstitial water
that has enough cohesive strength to prevent larger particles from settling but not
ou
g
h strength to prevent ow. Debris flows that have a matrix composed pre
dominantly of cohesionles sand and gravel are mud-free debris flows (Middle
ton, 1991). The support mechanism for tnes mud-free debris flows is poorly
understood.
After the yield strength of a debris flow has been overcome owing to water
saturation, and movement begis, the flow may continue to move over slopes as
low as 1°m 2° (Curray, 1966). Debris flows are believed to occur also in subaque
ous �nvironments, possibly as a result of miing at the downslope ends of sub
aqueous slumps. As subaqueous debris flows move rapidly downslope and ·are
diluted by lixing with more water, their strength is reduced, and they may pass
into turbidity currents. Deposition of the entire mass of debris flows and mud
ows occurs quickly. When the shear stress owing to gravity no longer exceeds
the yield strength of the base of the flow, the mass "freezes" and stops moving.
Debs-Flow Deposits
bris-flow deposits are thick, poorly sorted units that lack internalayering (Fig.
2.; Fig. 2.10). They typically consist of chaotic mixtures of particles that
may
range in size from clay to boulders. The large particles commonly show no pre
rred orientation. They are generally poorly graded, but if grading is present, it
ma
y
be either normal or reverse.
FURTHER READING
Figure 2.10
Poorly sorted debris-flow
deposits (Eocene), north
central Oregon. (Photo
graph courtesy of Abbas
Seyedolali)
Carling, P. A, and M. R. Dawson, 1996, Advances in iluvial
dynamics and strMigraphy: John Wiley & Sons, Chichester,
0 p.
Edwards, D. A., 1993, Turbidity currents: Dynamics, deposits
and reversals: Lecture Notes in EMth Sciences, Springer
Verlag, Berlin, 173 p.
Clifford, N., J. R. French, and J. Hrdisty (eds.), 1993, Turbulence:
Perspectives on ilow and sediment ansport; John Wiley &
ns, Chichester, 360 p.
Julien, P. Y, 1995, Erosion and sedimentation: Cambridge Uni
versity Press, Cambridge, 280 p.
48
Chapter 2 I Transport and Deposition of Siliciclastic Sediment
Leeder, M., 1999, Sedimentology and sedimentary basins: Black
well Science Ltd., Oxford, 592 p.
Middleton, G. , and J. B. Southard, 1984, Mechanics of sedi
ment movement: Soc. Econ. Paleontologists and Mineralo
gists Short Course Notes No. 3, 2nd ed., 401 p.
Middleton, G. V., and P. R. Wilcock, 1994, Mechanics in the earth
d environmental sciences: Cambridge University Press,
Cambridge, 459 p.
Pye, K., 1994, Sediment transport and depositional processes:
Blackwell Scientic Publications, Oxford, 397 p.
Yang, C. T., 1996, Sediment transport: Theory and practice: Mc
Graw-Hill Companies, Inc., New York, 396 p.

Physical Properties
of Sedimentary Rocks
Flute casts and groove
casts on the base of a tur
bidite sandstone bed
(Cretaceous), northern
Klamath Mountains,
California
49

50
T
he transport and depositional processes described in Chapter 2 generate a
wide variety of sedimentary rocks, each characterized by distinctive textur
al and structural properties. Sedimentary texture refers to the features of
sedimentary rocks that arise from the size, shape, and orientation of individual
sediment grains. Geologists have long assumed that the texture of sedimentary
rocks reflects the nature of ansport and depositional processes and that charac
terization of texture can aid in interpreting ancient environmental settings and
boundary conditions. An extensive literature has thus been published dealing
with various aspects of sediment texture, particularly methods of measuring and
expressing grain size and shape and interpretation of grain size and shape data.
The textures of siliciclastic sedimentary rocks are produced primarily by physical
processes of sedimentation and are considered to encompass grain size, shape
(form, roundness, surface texture), and fabric (grain orientation and grain-to
grain relations). The interrelationship of these primary textural properties con
trols other, derived, textural properties such as bulk density, porosity, and
permeability. The textures of some nonsiliciclastic sedimentary rocks such as cer
tain limestones and evaporites are also generated partly or wholly by physical
transport processes. The texture of others is principally caused by chemical or bio
chemical sedimentation processes. Extensive recrystallization or other diagenetic
changes may destroy the original textures of nonsiliciclastic sedimentary rocks
and produce crystalline textural fabrics that are largely of secondary origin. Obvi
ously, the textural features of chemically or biochemically formed sedimentary
rocks, and of rocks with strong diagenetic fabrics, have quite different genetic sig
nificance from those of unaltered siliciclastic sedimentary rocks.
Whereas the term "texture" applies mainly to the properties of individual
sediment grains, sedimentary structures, such as cross-bedding and ripple marks,
are features formed from aggregates of grains. These structures are generated by
a variety of sedimentary processes, including fluid flow, sediment gravity flow,
soft-sediment deformation, and biogenic activity. Because sedimentary structures
reflect environmental conditions that prevailed at or very shortly after the time of
deposition, they are of special interest to geologists as a tool for interpreting an
cient depositional environments. We can use sedimentary structures to help eval
uate such aspects of ancient sedimentary environments as sediment transport
mechanisms, paleocurrent flow directions, relative water depths, and relative cur
rent velocities. Some sedimentary structures are also used to identify the tops and
bottoms of beds and thus to determine if sedimentary successions are in deposi
tional stratigraphic order or have been overturned by tectonic forces. Sedimentary
structures are particularly abundant in coarse siliciclastic sedimentary rocks that
originate through traction transport or turbidity current transport. They occur
also in nonsilicidastic sedimentary rocks such as limestones and evaporites.

Sedimentary Textures
3.1 INTRODUCTION
T
his chapter focuses primarily on the physically produced textures of silici
clastic sedimentary rocks. Some of the special textural features that are im
portant to understandg the classification and genesis of limestones and
o nonsiliciclastic sedimentary rocks are discussed in Chapters 6 and 7. In this
chapter, we examine the characteristic textural properties of grain size and shape,
particle surface texture, and grain fabric and discuss the genetic significance of
ese properties. Although the study of sedimentary textures may not be the most
exciting aspect of sedimentology, it nonetheless an important field of
study. A
orough understanding of the nature and significance of sedimentary textures is
fundamental to interpretation of ancient depositional environments and transport
ntions, although much uncertainty still attends the genetic interpretation of
xtural data. Some long-standing ideas about the genetic significance of sediment
textural data are now being challenged, while new ideas and techniques for
studying and interpreting sediment texture continue to emerge. No textbook on
simentology would be complete without some discussion of sediment texture
d its genetic significance.
3.2 GIN SIZE
Grain size is a fundamental attribute of siliciclastic sedimentary rocks and thus
one of the important descriptive properties of such rocks. The sizes of particles in
a particuiar deposit reflect weathering and erosion processes, which generate par
ties of various sizes, and the nature of subsequent transport processes, as dis
sd in Chapter 2. Grains can range in se from day-size particles that require a
microscope for clear visualizaon to boulders several meters in diameter. dimen
los are particularly conceed with three aspects of particle size: (1) techques
for measurg grain size and expressing it in terms of some tpe of grain-size or
grade scale, (2) methods for summarizing large amounts of grain-size data and
psenting them in graphical or statistical form so that they can be mo easily
evaluated, and (3) the genetic (e.g., environmental) siificance of these data. We
wl now examine each of these conces.
51
52
Chapter 3 I Sedimenta Textures
Grain-Size scales
As mentioned, particles in sediments and sedimentary rocks range in size from a
few microns to a few meters. Because of this wide range of particle sizes, loga
rithmic or geometric scales are more useful for expressing size than are linear
scales. In a geomeic scale there is a succession of numbers such that a fixed ratio
exists between successive elements of the series. The grain-size scale used almost
universally by sedimentologists is the Udden-Wentworth scale. This scale, first
proposed by Udden in 1898 and modified and extended by Wentworth in 1922, is
a geometric scale in which each value in the scale is either twice as large as the
preceding value or one-half as large, depending upon the sense of direction
(Table 3.1). The scale extends from <1/256 mm (0.0039 mm) to >256 mm and is
divided into four major size categories (clay, silt, sand, and gravel), which can be
further subdivided (e.g., fine sand, medium sand, coarse sand). Blair and
McPherson (1999) suggest that the coarse end of the Udden-Wentworth scale be
divided into a greater number of subdivisions than those shown in Table 3.1 by
adding block (4.1-65.5 m), slab (65.5 m-1.0 km), monolith (1.0-33.6 km), and
megalith (>33.6 km).
A useful modification of the Udden-Wentworth scale is the logarithmic phi
scale, which allows grain-size data to be expressed in units of equal value for the
purpose of graphical plotting and statistical calculations. This scale, proposed by
Krumbein in 1934, is based on the following relationship:
= -log
2
d
(3.1)
where is phi size and d is the grain diameter in millimeters. For example, a grain
4 mm in diameter has a phi size of -2, which is the power required to raise the base
(2) of the logarithm to 4 (i.e., 2
2
). A grain 8 mm in size has a p value of -3 (the
base
2
3
). Some equivalent phi and millimeter sizes are shown in Table 3.1. Note
that the p scale yields both positive and negative numbers. The real size of par
ticles, expressed in millimeters, decreases with increasing positive phi values and
incases with decreasing negative values. Because sand-size and smaller grains
are the most abundant grains in sedimentary rocks, Krumbein chose the negative
logarithm of the grain size in millimeters so that grains of this size will have posi
tive phi values, avoiding the bother of constantly working with negative numbers.
This usage is also consistent with the common practice of plotting coarse sizes to
the left and fine sizes to the right in graphs.
Measuring Grain Size
The
size of siliciclastic grains can be measured by several techniques (Table 3.2).
e choice of methods is dictated by the purpose of the study, the range of grain
sizes to be measured, and the degree of consolidation of sedent or sedimentary
rock. Large particles (pebbles, cobbles, boulders) in either unconsolidated sedi
ment or liified sedimentary rock can be measured manually with a caliper or
tape. Grain size is commonly expressed in terms of eier the long dimension or
the intermediate dension of the particles. Granule- to silt-size particles un
consolidated sediments sedimentary rocks at can be disaggregated are com
monly
measured by sieving through a set of nested, wire-mesh screens (see
Ingram, 1971). The sieve numbers of U.S. Standard Sieves that correspond to vari
ous millimeter and phi sizes are shown in Table 3.1. Sieving techniques measure
the intermediate dimension of particles because e intermediate parcle size gen
eray determines whether or not a particle can go through a particular mesh.
Grain size of small, unconsolidated particles can also be measured by sedi
mentation techniques on the basis of the settling veloty of the particles. In these
techniques, grains are allowed to settle through a column of water at a specified

U.S. standard
Phi ()
sieve mesh
Millimeters
units
4096
-12
1024
-10
256
256
-8
-6
�
16
-4
�
5
4
4
-2
6
3.36
-1.75
7
2.83
-1.5
8
2.38
-1.25
10
2.00
2
-
1
.
0
12 1.68
.75
14
1.41
-o.s
16
1.19
-.25
18
1.00
1 0.0
20
0.84
0.25
25
0.71
0.5
30
0.59
0.75
35
0.50
%
1.0
a
0.42 1.25
z
45
0.35
1.5
50
0.30
1.75
�
60 0.25
1
/
4
2.0
70
0.210
2.25
80
0.177
2.5
100 0.149
2.75
120 0.125
%
3.0
140
0.105
3.25
170 0.088
3.5
200 0.074
3.75
230
0.0625
1/16
4.0
270 0.053
4.25
325
0.044
4.5
0.037
4.75
0.031
1
hz
5.0
0.0156
1
/
6.0
Q
0.0078
1
/
1
7.0
0
0.0039
1hs6
8.0
�
0.0020
9.0
0.00098
10.0
�
0.00049
11 .0
0.00024
12.0
u
0.00012
13.0
0.00006
14.0
t
e
mperature in a settling tube, and the time required for the grains to settle is mea
sured. For coarser particles (granules, sand, silt), the settling time of the particles is
reted empirically to a standard size-distribution curve (calibration curve) to ob
ta the equivalent millimeter or phi size (see, for example, Poppe, Eliason, and
Fredcks, 1985). As mentioned in Chapter 2, settling velocity of particles is affected
3.2 Grain Size
53
Wenorth size class
Boulder
Cobble
Pebble
Granule
Very coarse sand
Coarse sand
Medium sand
Fine sand
Very fine sand
Coarse silt
Medium silt
Fine silt
Very fine silt
Clay

54
Chapter 3 I Sedimentary Textures
Type of sample
Unconsolidated sediment
and disaggregated
sedimentary rock
Uthified sedimentary
rock
Sample grade
Boulders
Cobbles
Pebbles
Granules
Sand
Silt
Clay
Boulders
Cobbles
Pebbles
Granules
Sand
Silt
Clay
Method of analysis
Manual measurement of individual clasts
Sieving, settling-tube analysis, image
analysis
Pipette analysis, sedimentation balances,
photohydrometer, Sedigraph, laser-
diffractometer, electroresistance
(e.g., Coulter counter)
Manual measurement of individual clasts
Thin-section measument. image analysis
Electron microscope
by particle shape. Spherical parcles settle faster than nonspherical particles of the
same mass. Therefore, deteg the grain sizes of natural, nonspherical parti
cles by sedimentation techniques may not yield exactly the same values as those
determined by sieving.
The grain size of fine silt and clay particles can be determined by sedimenta
tion methods based on Stokes's Law (Chapter 2). The standard sedimentation
method for measuring the sizes of these small particles is pipette analysis (Gale
house, 1971). Pipette analysis is a laborious process because of e many opera
tions involved. To simplify these procedures, automatic-recording settling tubes
have now been developed that aow the sizes of both sand-size and clay-size sed
iment to be more easily and rapidly determined. Several other kinds of automated
particle-size analyzers are also available, each based on
a slightly different princi
ple. A photohydrometer is a settling tube that empirically relates changes in in
tensity of a beam of light passed through a column of suspended sediment to
particle settling velocities and thus to parcle size (Jordan, Fyer, and Hemmen,
1971). The Sedigraph determines particle size by measuring the attenuation of a
finely collated X-ray beam a nction of time and height in a settling suspen
sion (Stein, 1985; Jones, McCave, and Patel, 1988). A laser-diffracter size analyzer
operates on the principle that particles of a given size diffract light rough a
given angle, which increases with decreasing particle size (McCave et al., 1986).
Electroresistance size analyze, such as the Coulter count or Electrozone parti
cle counter, measure ain size on the basis of the principle that a particle passing
through an elecical field maintained in an electrolyte will displace its own vol
ume of the electrolyte and thus cause a change in the field. ese changes are
scaled and counted as voltage pulses; the magnitude of each pulse is proportional
to
particle volume (Swift, Schubert, and Sheldon, 1972; Muerdter, Dauphin, and
Steele, 1981). Semiautomated image analysis techniques use cameras to cap
ture and digitize grain images from which, with the aid of appropriate computer
software, grain-size diamers can be calculad (Kennedy and Mazzullo, 1991).
For a comparison of some of these analytical techniques, see Singer et al. (1988).
Additional information available in Principles, Methods, and Applications of Parti
cle Size Analysis, a monograph edited by Syvitski (1991).
