Blum W., Riegler W., Rolandi L. Particle Detection with Drift Chambers

Подождите немного. Документ загружается.

8.2 Quadratic Fit 299

8.2.4 Covariance Matrix at an Arbitrary Point Along the Track

Now we know the full covariance matrix of a, b and c at the centre of the chamber,

and we are curious to know the accuracy with which the measured track can be

extrapolated to some point x outside the centre. For this we must express the position

and the slope of the track as a function of the independent variable which deﬁnes

the distance from the track centre to the point in question:

a(x)=a

+ b

x +(c

/2)x

b(x)=b

+ c

x ,

c(x)=c

(8.27)

and c

represent the values of the coefﬁcients at the centre, for which the

covariance matrix was given in (8.23). The distance of the point x from the centre

of the chamber will be described by the ratio

r =

x −x

which has the same physical meaning as the r of (8.6) used in the linear ﬁt.

For example, to compute the covariance [a(x) c(x)],weform

[(a

+ b

x +(c

/2)x

) c

] ,

which is equal to [a

]+x[b

]+(x

/2)[c

]. In this way the full covariance matrix

is constructed, and the result is

(r)] =



+ r



−



+ r



N + 1

(r,N) ,

[a(r)b(r)] =





−



+ 2r



N + 1

(r,N) ,

(

(r)

)



+ 4r



N + 1

(r,N) ,

[a(r)c



−

+ 2r



N + 1

(r,N) ,

[b(r)c





N + 1

(r,N) ,

(

)





N + 1

(N) .

(8.28)

300 8 Geometrical Track Parameters and Their Errors

Apart from the dimensional factors in front of the square brackets, these covariances

depend only on r and N; they contain a common denominator N + 1, the number of

measurements. The remaining factors have been called B(r,N); they tend to a con-

stant as N → ∞, and they rapidly increase with r. The factors B

and B

belonging

to the diagonal elements [a

(r)] and [b

(r)] were calculated for some values of N

and r using (8.28) and (8.22). They are listed in Tables 8.3 and 8.4. The factor B

belonging to [c

] does not vary with r and was already contained in Table 8.2 in the

form of A

= B

(N)/(N + 1).

8.2.5 Comparison Between the Linear and Quadratic Fits

in Special Cases

Let us consider the extrapolation of a measured track to a vertex. The accuracy of

vertex determination is very different whether it happens inside a magnetic ﬁeld

with unknown track momentum or outside (or momentum known). We have a direct

comparison in Tables 8.1 and 8.3. It appears that a chamber whose front end is only

a quarter of its length away from the vertex (r = 0.75) extrapolates half as well

when inside a ﬁeld. This gets quickly worse when the vertex is further away – if the

factor of comparison is around 2.3 at r = 0.75, it is near 5 at r = 1.5. This depends

only weakly on the number of wires. It is obviously essential for a vertex chamber

that it be supported by a momentum measuring device with precision much better

than that of the vertex chamber alone.

The loss of accuracy owing to the presence of a magnetic ﬁeld is also important

for the measurement of direction. We want to compute the precision with which a

chamber can measure the direction of a track at the ﬁrst of N + 1 regularly spaced

wires. In the quadratic ﬁt we may use the third of equations (8.28) in conjunction

with Table 8.4 (last column), or we may evaluate the equation directly for r = 1/2,

which yields







12(2

+ 1)(8N −3)N

(N −1)(N + 1)(N + 2)(N + 3)

(quadratic ﬁt) . (8.29)

Table 8.3 Values of the factor B

(r, N) in (8.28) at various points along the track at distances r

from the centre of the chamber (in units of its length), for various numbers of N + 1 equally spaced

sense wires

Nr: 5 3 2 1.5 1 0.75 0.60 0.50

2 211 75.3 32.9 18.1 7.63 4.10 2.65 2.05

3 224 80.2 35.2 19.5 8.29 4.48 2.84 2.07

5 250 89.5 39.4 21.9 9.39 5.10 3.20 2.26

10 282 101 44.6 24.8 10.7 5.84 3.65 2.54

19 304 109 48.1 26.8 11.6 6.32 3.95 2.72

inﬁn. 335 120 53.0 29.5 12.8 7.00 4.37 3.00

8.2 Quadratic Fit 301

Table 8.4 Values of the factor B

(r, N) in (8.28) at various points along the track at distances r

from the centre of the chamber (in units of its length), for various numbers of N + 1 equally spaced

sense wires

Nr: 5 3 2 1.5 1 0.75 0.60 0.50

2 84.9 51.0 34.0 25.6 17.1 13.0 10.5 8.83

3 90.0 54.0 36.1 27.1 18.2 13.8 11.1 9.39

5 100 60.2 40.2 30.2 20.3 15.3 12.4 10.4

10 113 68.0 45.4 34.1 22.9 17.3 14.0 11.8

19 122 73.2 48.8 36.7 24.6 18.6 15.0 12.6

inﬁn. 134 80.6 53.8 40.4 27.1 20.4 16.5 13.9

In the linear ﬁt we use (8.8), where L was called x

−x

12N

(N + 1)(N + 2)

linear ﬁt . (8.30)

The ratio of the errors is

with bending

without bending



(2N + 1)(8N −3)

(N −1)(N + 3)



1/2

, (8.31)

which tends to 4 for inﬁnite N and is 3.60 for N = 2. This ratio is independent of

the magnetic ﬁeld and of the particle momentum as long as the curvature can be as

large as the uncertainty with which it is measured. If there is a priori knowledge that

the sagitta of the track is much smaller than the measurement error, the curvature

can be neglected, and (8.30) applies.

The fact that the directional error is dominated by the error in curvature is also

visible in their correlation coefﬁcient: with some algebra, we form the ratio

[b(

)c]

][b

(

)]

0.968

1−

(8.32)

and ﬁnd it almost equal to 1. This means the error in curvature produces almost

the entire error in direction. Figure 8.3 shows a picture of the case c = 0. Since

the sagitta is half as long as the corresponding distance between the chord and the

end-point tangent, we may estimate the directional error with

Fig. 8.3 Error

b in

direction, created by the

sagitta error

s. Case of zero

average curvature

302 8 Geometrical Track Parameters and Their Errors

b =

L/2

. (8.33)

Using (8.26),(8.24) and (8.29) one may verify that (8.33) is correct within 4% for

all N.

8.2.6 Optimal Spacing of Wires

With a given number N + 1 of wires and a given chamber length L the elements of

the covariance matrix can be minimized by varying the wire positions. Summarizing

Gluckstern [GLU 63] we mention that the optimal spacing is different for different

correlation coefﬁcients, and that for a minimal [c

] the best wire positions are ideally

the following:

(N + 1)/4 wires at x = 0, (N + 1)/2 wires at x = L/2 ,

(N + 1)/4 wires at x = L .

In practice the clustering of wires will use some of the chamber length. For the ideal

case this was set to zero, and he calculates at r = −1/2 that







N+1









= −

128

N+1

(

)

256

N+1

(8.34)

and this, at large N, is an important factor of 1.7 better in the momentum resolution

than (8.28).

8.3 A Chamber and One Additional Measuring

Point Outside

It happens quite often that tracks are measured not only in the main drift chamber

but in addition at some extra point which is located some distance away from the

main chamber. Typical examples are a miniature vertex detector near the beam pipe,

or a single layer of chambers surrounding the central main chamber. In an event with

tracks coming from the same vertex, the vertex constraint serves a similar purpose,

especially when the vertex position must be the same for many events. We suppose

that all the measurements happen inside a magnetic ﬁeld.

Since we have developed the covariance matrix of the variables a, b and c at an

arbitrary point r along the track, we have the tools to add the constraint of the one

additional space-coordinate measurement. The scheme to do this is the following.

8.3 A Chamber and One Additional Measuring Point Outside 303

Let the full covariance matrix at r (8.28) be abbreviated by

(r)=

⎛

⎜

⎝

(

(r)

)

[a(r)b(r)] [a(r)c]

[a(r)b(r)]

(

(r)

)

[b(r)c]

[a(r)c][b(r)c]

(

)

⎞

⎟

⎠

. (8.35)

This matrix has to be inverted to obtain the

matrix C

−1

(r). The corresponding

matrix D

−1

of the additional measuring point has only the one element that belongs

to the space-coordinate non-zero; let us call it 1/

(

is the accuracy of the addi-

tional measuring point):

−1

⎛

⎝

−2

000

⎞

⎠

. (8.36)

Now the covariance matrix E

of the total measurement, N + 1 regularly spaced

wires plus this one point, a distance rL away from their centre, is given by the

inverse of the sum of the inverses of the individual covariances:

)

−1

=(C

(r))

−1

+(D

)

−1

(8.37)

Now there is a theorem (e.g. [SEL 72]) which states that if the inverse of a ﬁrst

matrix is known, then the inverse of a second matrix, which differs from the ﬁrst in

only one element, can be calculated according to a simple formula. In our case the

ﬁrst matrix is C

−1

, and its known inverse is C; the second matrix, E

−1

, differs from

the ﬁrst only in the (1, 1) element which is larger by 1/

. The inverse of the second

matrix is given by

= C

−

. (8.38)

This means that our covariance matrix (8.28) changes by the addition of one point

at r according to the following scheme (we leave out the argument r):

(

)

→ [a

2

]=[a

] −

]

+[a

]

[ab] → [a



]=[ab] −

][ab]

+[a

]

(

)

→ [b

2

]=[b

] −

[ab

]

+[a

]

[ac] → [a



]=[ac] −

][ac]

+[a

]

[bc] → [b



]=[bc] −

[ab][ac]

+[a

]

(

)

→ [c

2

]=[c

] −

[ac]

+[a

]

(8.39)

304 8 Geometrical Track Parameters and Their Errors

8.3.1 Comparison of the Accuracy in the Curvature Measurement

We are particularly interested in the gain that can be obtained for the curvature

measurement. Introducing the ratio f

/[a

(r)] (how much better the extra mea-

surement is compared to the extrapolated point measuring accuracy of the chamber),

we write the gain factor as

( f ,r)=

] −

[a(r)c]

+[a

(r)]

]

= 1−

[a(r)c]

(1+ f

)[a

(r)][c

]

. (8.40)

Since the covariance matrix (8.28) is a function of r and N,

also depends on N.We

evaluate (8.40) in the limit of N → ∞. Table 8.5 contains the result.

It appears that considerable improvement is possible for the curvature, and hence

momentum, measurement of a large drift chamber when one extra point outside

can be measured with great precision. This is a consequence of the increase of the

lever arm. As an example we consider the geometry of the ALEPH TPC. For a

well measured track there are 21 measured points, equally spaced over L = 130cm;

each has

= 0.16mm, and therefore

√

(720/25) ×(0.16 ×10

−3

)/1.30

5.1 ×10

−4

−1

, according to (8.24). A silicon miniature vertex detector with

0.02mm,35cm in front of the ﬁrst measuring point (r = 0.77), would result in an

improvement factor of

= 0.40, according to Table 8.5. Here we have determined

√

(0.77)] = 7×0.16mm/

√

21 = 0.24mm, using the ﬁrst of (8.28) and Table 8.3;

therefore f = 0.02/0.24 = 0.08.

Such enormous improvement could only be converted into fact if all the system-

atic errors were tightly controlled at a level better than these 20

m. Also, for the

moment we have left out any deterioration caused by multiple scattering, to which

subject we will turn in Sect. 8.4.

8.3.2 Extrapolation to a Vertex

Since it is the ﬁrst purpose of a vertex detector to determine track coordinates at a

primary or secondary interaction vertex, we must carry our error calculation forward

Table 8.5 Factors

( f , r) of (8.40) by which the measurement of curvature becomes more accu-

rate when a single measuring point with accuracy

= f

√

(r)] is added to a large number of

regularly spaced wires at a distance rL from their centre

: 0 0.1 0.2 0.3 0.5 1.0 2.0

0.5 0.67 0.70 0.73 0.76 0.79 0.85 0.90

0.6 0.53 0.59 0.63 0.67 0.72 0.80 0.87

0.7 0.43 0.51 0.57 0.61 0.68 0.77 0.85

0.8 0.37 0.46 0.53 0.58 0.65 0.75 0.84

1.0 0.28 0.40 0.48 0.54 0.62 0.73 0.83

1.5 0.18 0.35 0.44 0.51 0.60 0.72 0.82

2.0 0.13 0.33 0.43 0.49 0.59 0.71 0.82

inﬁn. 0 0.30 0.41 0.48 0.58 0.71 0.82

8.3 A Chamber and One Additional Measuring Point Outside 305

Fig. 8.4 Extrapolation of the

quadratic ﬁt to a vertex

located a distance x in front of

a vertex detector with

accuracy ±

.TheN +1

wires of a chamber are

uniformly spaced over the

length L. The vertex detector

is a distance x

away from the

centre of the wires. In the

text, r = x

to the vertex. The situation is sketched in Fig. 8.4. The coordinate x represents the

distance of the detector to the vertex, and the extrapolation error

of the vertex

position is given by the covariance

=[y

]=[(a



(r)+b



(r)x + c



(r)x

/2)

]

=[a

2

]+2x[a



]+x

([b

2

]+[a



])

+ x



]+x

2

]/4 .

(8.41)

Here the [a

2

],[a



],... represent the elements of the covariance matrix E (8.39) at

the position r of the vertex detector.

The evaluation of (8.41) is too clumsy when done in full generality, and we will

consider the special case of a vertex detector that is much more accurate than the

drift chamber at r, as presented in Table 8.3:

 1

 [a

(r)] . (8.42)

The covariance matrix at r for the ensemble of chamber and vertex detector, in ﬁrst

order of

/[a

(r)], takes the form

E =

⎛

⎜

⎝

[ab]/[a

]

[ac]/[a

]

[ab]/[a

][b

] −[ab]

/[a

][bc] −[ab][ac]/[a

]

[ac]/[a

][bc] −[ab][ac]/[a

][c

] −[ac]

/[a

]

⎞

⎟

⎠

. (8.43)

The elements of E depend on N and r. We evaluate (8.43) in the limit of N →∞ and

for some special values of r.Forr = 1/2 (i.e. the vertex detector at the same place

as the last wire), using (8.41), (8.42), (8.28), (8.22), one ﬁnds that

N + 1



+ 120

+ 80





1+ 8.0

+ 6.7



306 8 Geometrical Track Parameters and Their Errors

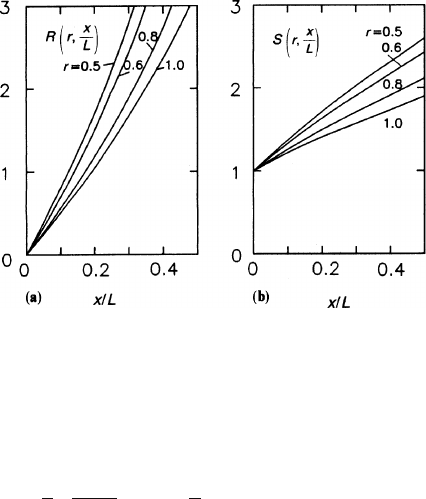
Fig. 8.5a,b Graph of the two

functions in (8.44) for four

positions r of the vertex

detector; (a) R(r, x/L),(b)

S(r, x/L)

Here we have counted x/L positive if x and x

point in the same direction. We see

that the vertex extrapolation accuracy deteriorates as x/L increases. There is one

term proportional to the accuracy squared of the vertex detector alone, and one term

proportional to the quantity

/(N +1), which characterizes the accuracy of the drift

chamber.

= R





N + 1

+ S





. (8.44)

Figure 8.5a,b contains graphs of R(r,x/L) and S(r,x/L) for four values of r in the

range of typical applications.

Taking again the geometry of the ALEPH experiment as a numerical example,

we read from Fig. 8.5a,b that for r = 0.77 and x

= 6.5cm the vertex extrapolation

accuracy can reach

√

(0.28

/21 + 1.14

). Using

= 160μm and

20μm one obtains

= 25μm in this particular case.

8.4 Limitations Due to Multiple Scattering

The achievable accuracy of a chamber may be reduced by multiple scattering of the

measured particle in some piece of the apparatus. There it suffers a displacement

and a change in direction, and we want to know the inﬂuence on the accuracy of

vertex reconstruction and of momentum measurement.

8.4.1 Basic Formulae

The theory of multiple scattering has been developed by Moliere, Snyder, Scott,

Bethe and others. Reviews exist from Rossi [ROS 52], Bethe [BET 53] and Scott

[SCO 63]. Our interest here must be limited to the basic notions.

8.4 Limitations Due to Multiple Scattering 307

After a particle has traversed a thickness x of some material, it has changed its

direction and position, and we want to know the two-dimensional probability distri-

bution P(x, y,

) of the angular and spatial variables

and y. Here we describe in a

Cartesian coordinate system the lateral position at a depth x by the coordinates y and

z. The corresponding angles are denoted by

(in the x–y plane) and

(in the x–z

plane). Because of the symmetry of the situation, the two distributions P(x,y,

) and

P(x,z,

) must be the same. In the simplest approximation they are given [ROS 52]

P(x,y,

)dy d

√

exp



−



−



, (8.45)

where the only parameter

is called the mean square scattering angle per unit

length. The angular distribution, irrespective of the lateral position, is given by the

integral

Q(x,

∞



−∞

P(x,y,

)dy =

√

exp



−



. (8.46)

We have for this projection a Gaussian distribution with a mean square width of



 =

x/2 . (8.47)

Since the basic process is the scattering with a single nucleus, we understand

that the variance of

must be proportional to the number of scatterings, and

hence x.

The corresponding spatial distribution, irrespective of the angle of deﬂection, is

given by the integral over the other variable:

S(x,y)=

∞



−∞

P(x,y,



√

exp



−



. (8.48)

This Gaussian distribution has a mean square width of

y

 =

/6 . (8.49)

For completeness we mention that the covariance is given by

y

 =



P(x,y,

)dy d

= Θ

/4 . (8.50)

The mean square scattering angle per unit length,

, depends on particle veloc-

ity

and momentum p as well as on the radiation length X

rad

of the material:





rad

. (8.51)

308 8 Geometrical Track Parameters and Their Errors

The constant E

, which has the dimension of energy, is given by the ﬁne-structure

constant

and the electron rest energy mc





1/2

= 21MeV . (8.52)

Using (8.52) and (8.51) in (8.50) and (8.49) we may express the projected r.m.s.

deﬂection and displacement as



 =

15MeV



rad

, (8.53)

y

 =



 . (8.54)

A short list of scattering lengths for some materials of interest in our context is given

in Table 8.6. It is extracted from [TSA 74]; see also [PAR 04].

In Moliere’s theory [MOL 48], which represents the measurements very well

(see BET 53), the Gaussian distribution of the scattering angle is only one term in a

series expansion. The effect of the additional terms is that the Gauss curve acquires

a tail for angles that are several times as large as the r.m.s. value. Although only at

the level of a few per cent compared to the maximum, they are many times larger

than the Gauss curve for these arguments. The tail is caused by the few rare events

where one or two single scatters reach a deﬂection several times as large as the r.m.s.

Table 8.6 Radiation lengths X

rad

and densities

of some materials relevant for drift chambers

Material

rad

Gases (N.T.P.) (g/l) (m) (g/cm

)

0.090 6800 61.28

He 0.178 5300 94.32

Ne 0.90 321.6 28.94

Ar 1.78 109.8 19.55

Xe 5.89 14.4 8.48

Air 1.29 284.2 36.66

1.977 183.1 36.2

0.717 648.5 46.5

Iso−C

2.67 169.3 45.2

Solids (g/cm

)(cm)(g/cm

)

Be 1.848 35.3 65.19

C 2.265 18.8 42.70

Al 2.70 8.9 24.01

Si 2.33 9.36 21.82

Fe 7.87 1.76 13.84

Pb 11.35 0.56 6.37

Polyethylene CH

0.92–0.95 ∼ 47.9 44.8

Mylar C

1.39 28.7 39.95