Blum W., Riegler W., Rolandi L. Particle Detection with Drift Chambers

Подождите немного. Документ загружается.

268 7 Coordinate Measurement and Fundamental Limits of Accuracy

This is the principal limit of the coordinate measuring accuracy using pads;

and

were deﬁned in Fig. 7.7. In the usual case of no declustering, the values of

eff

for argon can be taken from Fig. 1.22.

7.3.4 Consequences of (7.33) for the Construction of TPCs

The relative size of the three terms in (7.33) depends, ﬁrstly, on the diffusion of the

electrons during their drift. In the presence of a typical longitudinal magnetic ﬁeld,

the magnetic anisotropy of diffusion will make the ﬁrst term the smallest one on

average, for any practical choice of b and h.

In the usual case, a pad extends over several wires, and h is much larger than b;

therefore the third term will dominate even for a small

. The most critical coordi-

nate measurements are those for a determination of large track momenta on tracks

with a small curvature. The pad rows should therefore be oriented at right angles to

these critical tracks, so that, for them,

≈ 0. For this reason, the ALEPH and the

DELPHI TPCs have circular pad rows.

With the choice of h the designer of the TPC wants to take advantage of the

fact that N(h) increases in proportion to h and N

eff

(h) approximately in proportion

√

h. Also, the larger the collected amount of charge on a pad the less critical is

the noise of the electronic ampliﬁer. On the other hand the third term in (7.33) can

be kept small only within a range of

which becomes smaller and smaller as h

is increased. Even the modest magnetic bending of a high-momentum track may

exceed this range if h is made too large. It can be shown that the consequence is

a constant limiting relative-momentum-measuring accuracy

p/p rather than one

which decreases as p is reduced.

Problems of double-track resolution are discussed in Sect. 11.7.1

7.3.5 A Measurement of the Angular Variation of the Accuracy

The second term in (7.33) can be studied in detail by measuring

AV P

as a function

, keeping

ﬁxed at 0. This has been done by Blum et al. [BLU 86] using a small

TPC with rotatable wires in a beam of 50 GeV muons. Each track had its transverse

position measured at four points using the pulse heights on the pads (see Fig. 7.11).

The pad length h was 3 cm and the wire pitch b was 4 mm. The variance was deter-

mined for every track as one half the sum of the squared residuals of the straight-line

ﬁt. The result is

, the measured variance averaged over many tracks, as a function

of the angle

between the tracks and the normal to the wires. According to (7.33)

should vary as

12N

eff

(tan

−tan

)

cos

12N

eff

sin

(

−

)

cos

, (7.34)

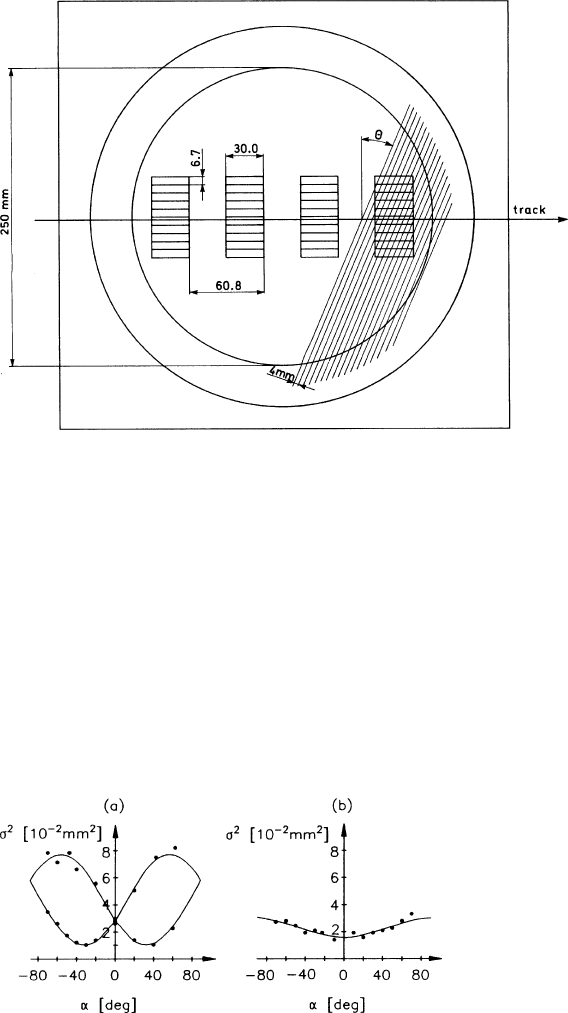
7.3 Accuracy in the Measurement of the Coordinate 269

Fig. 7.11 Layout of TPC with rotatable wires [BLU 86]

where

contains the effects of diffusion and, perhaps, of the electronics and any

remaining contribution of the angular pad effect.

The results are depicted in Fig. 7.12a,b. The curves represent ﬁts to (7.34) on ad-

justing the three free parameters

and N

eff

(h,

/b). A reversal of the magnetic

ﬁeld changes the sign of

so that two curves are seen in Fig. 7.12a,ba. The values

of the ﬁtted parameters are shown in Table 7.2.

Keeping in mind that a magnetic ﬁeld of 1.5 T reduces the transverse diffu-

sion coefﬁcient by a factor 50 (cf. Sect. 2.4.5) we expect for the mean square

width of the diffusion cloud after 4 cm of drift a value of 1.6mm

(B = 0) or

3.2×10

−2

(B = 1.5T). Since on a pad length of 3 cm the number of ionization

Fig. 7.12a,b The square of the measuring accuracy

determined by [BLU 86] as a function of

the track angle

,(a) in a magnetic ﬁeld of ±1.5T, (b) without magnetic ﬁeld. The continuous

lines were calculated using (7.34) with the ﬁtted parameters of Table 7.2

270 7 Coordinate Measurement and Fundamental Limits of Accuracy

Table 7.2 Parameters ﬁtted to the measured accuracy

according to (7.34) for two values of the

magnetic ﬁeld (gas: Ar (90%)+CH

(10%))

B(T)

(mm

) N

eff

(deg)

1.5 (1.08 ±0.03)10

−2

27.8±0.632.3±1.5

0 (1.58 ±0.06)10

−2

83±8 −1±2

electrons is approximately 300, the expected change in the uncertainty of the centre

is 0.5×10

−2

, equal to the measured difference in

appearing in Table 7.2.

The increase by a factor of three in the parameter N

eff

, connected with the re-

moval of the B ﬁeld, is attributed to the declustering effect: as the width of the

diffusion cloud increases it becomes comparable to b, more electrons from the same

cluster arrive on different wires, and N

eff

goes up. The increase does not occur when

the tracks are produced by a laser ray rather than a particle.

The angle

of electron drift near the wire was 32

◦

at 1.5 T in gas composed of

argon (90%) and methane (10%). This value depends strongly on the gas and on the

electric ﬁeld near the sense wires. The wire and ﬁeld conﬁguration employed here is

characteristic of TPCs and is described in the case studies in Sect 3.1.2. The tangent

is found to be roughly proportional to B.

7.4 Accuracy in the Measurement of the Coordinate

in the Drift Direction

In Sect. 7.2 we pointed out that there is a symmetry between the two situations sym-

bolized in Figs. 7.1 and 7.2, the coordinate measurement along the wire and along

the drift direction. The variances (7.5) and (7.9) of the single-electron coordinate

are basically the same if one employs the substitution rule (7.10); this holds under

the assumption that the time of arrival of the drifting electron at the entrance of the

wire region is the same, up to a constant, as that recorded by the electronics.

We must now complement this argument by the observation that for most drift

chambers this last approximation is too crude. Figure 7.2 shows that, owing to the

shape of the velocity ﬁeld lines in the wire region, even electrons produced by a

track at

= 0 have different paths before reaching the wire: electrons collected at

the edge of the cell have to drift more than those collected in the middle.

The isochronous lines in the wire region have almost a parabolic shape and can

be approximated by

z = z

−a

where a is a dimensionless constant of the order of unity, which depends on the

shape of the ﬁeld lines in this region. In the example of Fig. 7.2, a = 0.8.

The arrival time t on the wire of a single electron entering the wire region at y at

the time t is then

7.4 Accuracy in the Measurement of the Coordinate in the Drift Direction 271

t = t





+ a



. (7.35)

The average and variance of this last expression on the distribution (7.7) are

t =



+ a



, (7.36)

t

−t



tan

180



, (7.37)

where the last and new term is the contribution of the drift-path variations in the

wire region.

7.4.1 Inclusion of a Magnetic Field Parallel to the Wire Direction:

the Drift E×B Effect

Drift chambers with precise measurements of the track coordinates along the drift

direction are often operated with a magnetic ﬁeld perpendicular to the drift direction

and parallel to the wires. With this conﬁguration one can obtain a precise determi-

nation of the curvature induced on the particle trajectory by the magnetic ﬁeld, and

the momentum of the particle can be determined (see Chap. 8 for details).

If a magnetic ﬁeld perpendicular to the drift electric ﬁeld is present, the drifting

electrons have to move transverse to it. This produces an E ×B force according to

(2.6) and causes the electrons to drift under an effective angle

with respect to the

direction of the electric ﬁeld. The angle

is such that tan

ωτ

, where

is the

cyclotron frequency and

is the time between two collision suitably averaged.

Electrons produced by a track at

= 0 do not arrive simultaneously at the en-

trance to the wire region, but their arrival positions depend linearly on y with a slope

tan

The variance of the arrival time of a single electron depends now on the angle

t

−t



tan

(tan

−tan

)

180



, (7.38)

where the diffusion parameter

refers to the new drift direction, and

to the

direction perpendicular to it and to the magnetic ﬁeld. The two parameters are not

necessary equal, owing to the electric anisotropy of diffusion (cf. Sect. 2.2.5), but

for simplicity we will replace them below by a common value.

Up to now we have dealt with the drift-time variations of a single electron. When

a measurement is performed, the whole swarm arrives. There are various ways to

extract the time information. In terms of electronics, one may either employ discrim-

inators of various types in order to trigger on the ﬁrst electrons, or on the centroid

of the pulse or on some other value based on a threshold-crossing time. Or one may

apply a very fast sampling technique in order to obtain a numerical representation of

272 7 Coordinate Measurement and Fundamental Limits of Accuracy

the pulse shape, which may be used to derive a suitable estimator. We discuss here

two estimators of the arrival time of the swarm: the average and the Mth electron,

assuming for simplicity

= 0.

7.4.2 Average Arrival Time of Many Electrons

When we average over the arrival times of all the electrons, the statistical reduction

of the different terms of (7.38) is not the same because of the correlation between

electrons produced in the same cluster. Following the lines of Sect. 7.2 we can write

the variance of the average arrival time as

TAV



cos

eff



tan

180



, (7.39)

where N represents the total ionization collected by the wire, and N

eff

is the effective

number of independent electrons.

The contribution of the drift-path variation of the variance of the average is al-

ways present, even for tracks in good geometry (

= 0) and close to the wire

(

≈0). It is quite large and increases with b more than linearly, since N

eff

increases

with the track length more slowly than in proportion.

Obviously the average over all arrival times ﬂuctuates so badly because of the

late-arriving electrons, those that have to take the longest path when they approach

the wire. If one derives the time signal from the few electrons that arrive ﬁrst, the

latecomers do not contribute. In fact, a discriminator with a low threshold will do

this automatically.

7.4.3 Arrival Time of the Mth Electron

Let the time signal be deﬁned by the moment that the Mth electron arrives. Here M

can either be a ﬁxed number (this is the case when a ﬁxed-threshold discriminator

is used) or a given fraction of the total number of electrons contributing (this is the

case of a constant-fraction discriminator).

The probability p(t) of one electron arriving before the time t is calculable using

(7.7) and (7.35):

p(t)=



−∞

f (



+∞

−∞

f (

, (7.40)

where

f (

+b/2



−b/2

dyf

(

−(z

+ ay

/b)/u,y)d

. (7.41)

Next we have to write out the probability R(t) that the Mth electron out of a

group of N arrives in the interval dt. It is equal to the probability that any one of

7.4 Accuracy in the Measurement of the Coordinate in the Drift Direction 273

the N electrons arrives precisely in dt (equal to N (dp/dt)orN dp) multiplied by the

probability that any of (M −1) out of the (N −1) remaining ones arrives before t

and the rest after t + dt:

R(t)dt = N



N −1

M −1



M−1

(1−p)

N−M

= M





M−1

(1−p)

N−M

dp = P(p)dp. (7.42)

In the last expression we have deﬁned a probability density P(p) for the variable p.

It is easy to show that

+∞



−∞

R(t)dt =



P(p)dp = 1 .

Here and in the following steps we make use of the well-known expression for

the deﬁnite integral



(1−x)

dx =

j!k!

( j + k + 1)!

The variance of the arrival time of the Mth electron is given by

= t

−t

with

t

 =

+∞



−∞

R(t)dt =



(p)P(p)dp

and

t =

+∞



−∞

tR(t)dt =



t(p)P(p)dp . (7.43)

The function t(p) is obtained by inverting (7.40).

We consider now separately the two contributions of the difference of the drift

paths and of the diffusion and study the particular case of a track perpendicular to

the drift velocity direction (

= 0).

7.4.4 Variance of the Arrival Time of the Mth Electron:

Contribution of the Drift-Path Variations

In order to study the effect of the drift-path variation alone we go to the limit

→ 0,

→ 0 of (7.41) at

= 0, and obtain

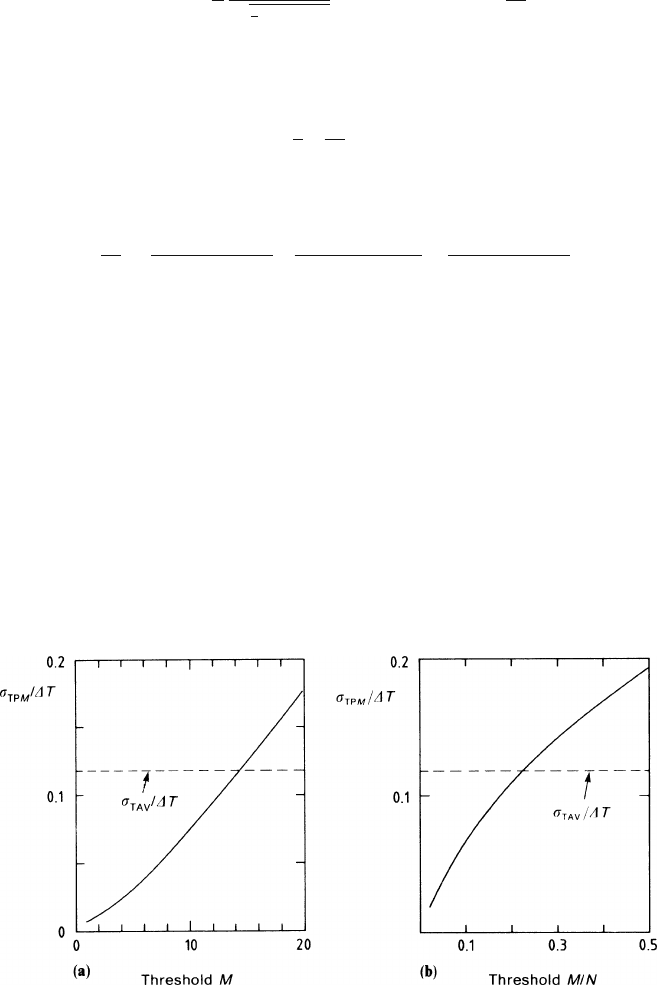
274 7 Coordinate Measurement and Fundamental Limits of Accuracy

f (t)dt =



(tu−z

)

dt, 0 ≤ (tu−z

) ≤

(7.44)

and f (t)=0 outside of this time interval. Using this expression we can evaluate

p(t) from (7.40) and invert it:

t(p)=



+ z



. (7.45)

Now we compute the integrals (7.43) and use this expression for t(p):

TPM





M(M + 1)

(N + 1)(N + 2)



(M + 2)(M + 3)

(N + 3)(N + 4)

−

M(M + 1)

(N + 1)(N + 2)



. (7.46)

This is the variance in the arrival time of the Mth electron among N independent

ones when only the drift-path variation is taken into account.

If we want to apply this formula to a practical case we have to use for N the

number of clusters, and we realize that because of the cluster-size ﬂuctuations it

describes correctly only the case M = 1, since the threshold can only be set at a

certain number of electrons and not of clusters.

In order to take into account the cluster-size ﬂuctuations we have to use a Monte

Carlo program. Figure 7.13a,b shows the result of a simulation of the distribution of

the arrival times, assuming the conditions valid for 1 cm of argon gas at NTP (and

27 clusters/cm). In both parts of the ﬁgure the r.m.s. of the arrival time is normalized

to the width of the collection time interval:

T = ab/4u .

Fig. 7.13a,b R.m.s. variation of the arrival time of the Mth electron in 1 cm of argon, caused by

differences in drift-path length, (a) as a function of M,(b)whenM is a ﬁxed fraction of the total

number of electrons N. The r.m.s. of the average time is also shown. (See text for explanations.)

7.4 Accuracy in the Measurement of the Coordinate in the Drift Direction 275

Also visible is the r.m.s. of the average (7.39), evaluated for

= 0,

= 0, N

eff

= 6

and normalized to the same quantity. We observe that the limit of the accuracy due

to the drift-path variation can be made very small by lowering the threshold. For

example,

comes down to 30% of

TAV

when triggering on a value of M equal

to 5% of N. But by gaining on the drift-path variations, one loses on the diffusion

term.

7.4.5 Variance of the Arrival Time of the Mth Electron:

Contribution of the Diffusion

Next we study the contribution of diffusion. The probability density f (t) of (7.41)

with a = 0 and

= 0 takes the form

f (t)dt =

exp



−

(

t−

)



√

πσ

dt , (7.47)

and the function p(t) of (7.40) is the function E:

p(t)=E



t −z



t−z



−∞

exp(−q

/2)

√

. (7.48)

To compute the variance of the arrival time of the Mth electron we should solve

the integrals (7.43) using the function t(p) deﬁned by the inverse of (7.40).

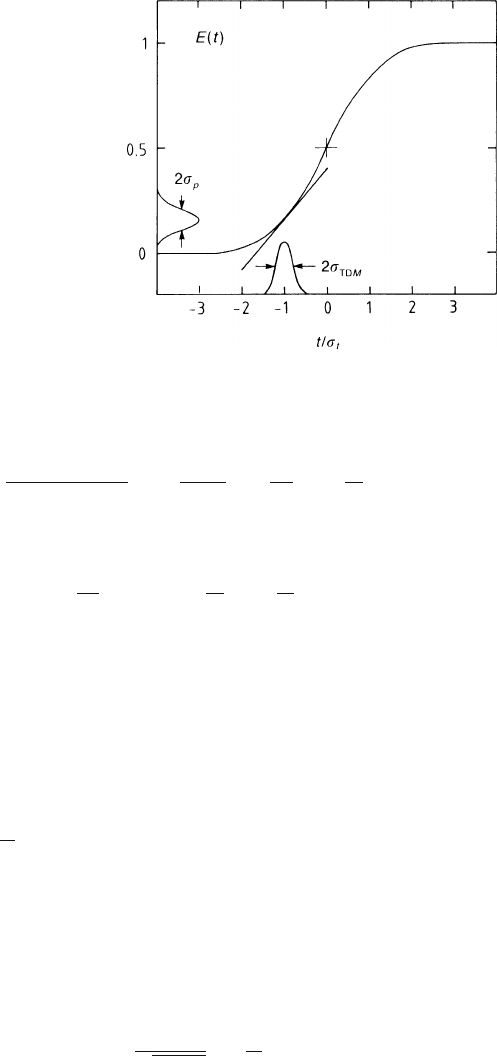
Since we cannot invert the expression (7.48) analytically, we linearize it in the

vicinity of the average value of the function P(p) of (7.42). This procedure is justi-

ﬁed by the fact that the variance of the function P(p) is small when M is small and N

large. It is illustrated in Fig. 7.14. The variance of the arrival time is the variance of

p on the probability distribution P(p) projected onto the t axis using the derivative

dE(q)

√

exp



q



evaluated at q deﬁned by p = E(q).

The variance of p is given by

p

 =



P(p)dp =

N + 1

and

p

 =



P(p)dp =

M(M + 1)

(N + 1)(N + 2)

276 7 Coordinate Measurement and Fundamental Limits of Accuracy

Fig. 7.14 Illustration of

(7.50): the variance of p is

projected onto the time axis

using the tangent to the error

function erf(t) in order to

obtain

TDM

from which we obtain

p

−p

(N + 1)(N + 2)



1−

N + 1



≈



1−



. (7.49)

Projecting now this variance onto the time axis (see Fig. 7.14) we obtain

TDM

≈

exp(q

)



1−



, (7.50)

where q is the normalized average arrival time, given by the condition that the

corresponding integral probability p takes on the value M/(N + 1), or in good ap-

proximation, M/N. In other words, q is given by the inverse of the function E at

its argument M/N :

q = E

−1

(M/N) . (7.51)

Expression (7.50) with (7.51) represents the answer to the question how much the

arrival time of the Mth electron ﬂuctuates when each single electron has a Gaussian

distribution with a width

;

TDM

goes down with the total number N of electrons

and is equal to

√

N times a factor which depends only on M/N. The factor de-

scribes the loss of accuracy when the arrival-time measurement is based on the Mth

electron rather than on the average of all N. (The variance

TAV

of the average ar-

rival time caused by diffusion alone was

/N as implied by (7.39).) The loss factor

is plotted in Fig. 7.15 and is seen to be always larger than 1. For example the loss is

a factor 2 if one triggers on the ﬁrst 5% of the swarm.

An often-quoted formula according to which

TDM

√

2logN

∞

∑

r=M

(7.52)

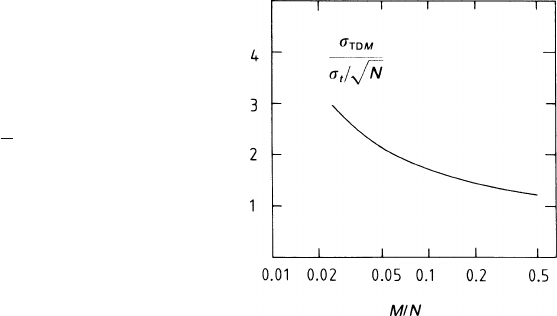
7.5 Accuracy Limitation Owing to Wire Vibrations 277

Fig. 7.15 Errors of time

measurement caused by

diffusion: r.m.s. variation

TDM

of the arrival time of

the Mth electron, in units of

the r.m.s. variation of the

average arrival time of N

electrons,

√

N, plotted as

a function of M/N

instead of (7.50) has been discussed by Cramer [CRA 51]. The right-hand side of

(7.52) is the ﬁrst term of a power series in 1/logN. It turns out that for M = 1 (7.52)

is more accurate than (7.50), but it cannot reproduce the variation of

TDM

with M.

We conclude this section with a comment on the various ways to estimate the

time of arrival of the electron swarm. It is clear from the previous pages that this is

a question of the relative importance of the two main contributions to the measure-

ment accuracy. Where the drift-path variations are relatively large, one gains a lot

by triggering on a low threshold. Where the diffusion is relatively large, one gains,

but not so much, by using the average. The contribution from the angular effect and

from the effect of the drift-path variations quickly increase as the angle

increases.

Since the diffusion increases with the drift length, the relative importance of the two

contributions changes through their dependence on

and N

eff

, and the best estima-

tor is a function of the drift length. Depending on how far one wants to go in the

optimization, the fast sampling technique offers the greatest freedom.

7.5 Accuracy Limitation Owing to Wire Vibrations

Up to this point we have had two phenomena which, in functioning together, pro-

duce fundamental limitations on the accuracy of coordinate measurement: diffusion

and ionization ﬂuctuation. As we have seen in this chapter, these limitations are fun-

damental in the sense that they are inherent in the measuring process and cannot be

overcome by removing technical imperfections.

After the appearance of the ﬁrst edition of this book, a new phenomenon was de-

scribed which also limits the accuracy of coordinate measurement in a fundamental

way: wire vibrations caused by the avalanches on the sense wire [BOY 95]. Every

avalanche exerts a repulsive force onto the wire as long as the positive ions are on

their way to the cathode. Upon their arrival at the cathode they have conveyed a

tiny bit of momentum to the wire. In an environment of heavy background radiation