Blum W., Riegler W., Rolandi L. Particle Detection with Drift Chambers

Подождите немного. Документ загружается.

258 7 Coordinate Measurement and Fundamental Limits of Accuracy

diffusion are collected by the wire:

∑

j=1

= N . (7.11)

In general not all the electrons produced in the same cluster are collected by the

wire because of the random diffusion along the drift path.

The variance of X

is by deﬁnition

−





, (7.12)

where the average is taken over the probability distribution f





∑

x



b/2



−b/2

+∞



−∞

(x,y)dx = x

(7.13)

and

∑

x

 . (7.14)

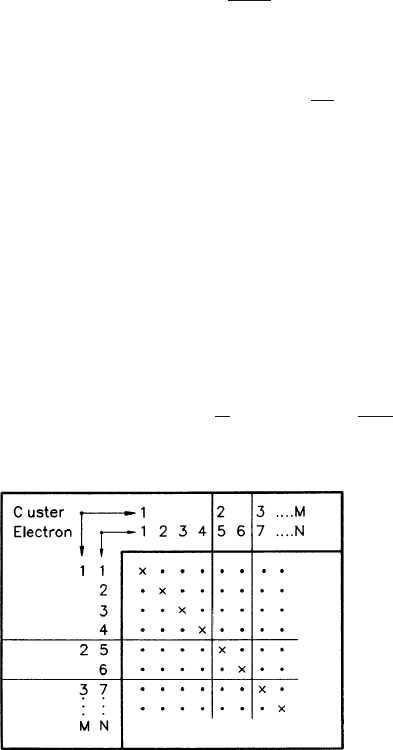
The sum in the last equation contains three different kinds of terms; refer to

Table 7.1 for a graphical representation. When i = j then x

 = x

. There are

N terms of this kind; they are marked by crosses in the table. When i = j and the

electrons do not belong to the same cluster, then x

= x

, because two different

ionization processes are not correlated. There are N

−

∑

terms of this kind, they

are represented by the dots in the rectangular boxes of the table. When i = j and the

electrons do belong to the same cluster (the dots in the square boxes), then x

and x

are correlated. We deﬁne the average x

= xx. There are

∑

−N terms of this

kind.

Using (7.12–7.14) one ﬁnds that the variance is equal to

(x

−xx)+

∑

(xx−x

) . (7.15)

Table 7.1 Classiﬁcation of the pairs of all electrons from a track that were collected on one wire

7.2 Basic Formulae for a Single Wire 259

In the absence of diffusion, xxis equal to x

and the ﬁrst term of (7.15) is zero,

so we obtain the result derived in Sect. 1.2, where the quantity

∑

was deﬁned

as 1/N

eff

. If all the clusters consisted of one electron, the term

∑

there became

equal to 1/N and we obtained the standard formula of the variance of the mean.

We may therefore distinguish the following limiting cases of (7.15):

• Limit of no diffusion, using (7.5):

→

eff

(x

−x

eff

tan

. (7.16)

• Limit of no clustering, using (7.5) and

→

(x

−x



cos

tan



. (7.17)

• Limit

= 0, in the presence of clustering:

→

. (7.18)

In (7.16–7.18), N

eff

is the effective number and N is the total number of elec-

trons on the track segment delimited by the cell width; their values are

-dependent

through the length of the track segment.

An analytical expression of the covariance xx in (7.15) is derived under certain

assumptions in the appendix to this chapter, resulting in formula (7.81) for

This can be rewritten in the form

→



cos



eff

tan

. (7.19)

where the quantities N



and N



eff

depend on

as well as on

and b.

Let us ﬁrst deal with the term proportional to (b

/12)tan

. We may regard N



eff

as the effective number of electrons that would cause the same ﬂuctuation as the

combined action of ionization plus diffusion, thus extending the original meaning

of N

eff

deﬁned in Sect. 1.2 and used in (7.16).

The quantity N



eff

, for which an analytic expression is given in the

appendix to this chapter, can also be calculated with a numerical simulation of the

ionization and diffusion process. In order to compute it as a function of the diffusion

parameter

we evaluate the variance V

of the average of the coordinates along

the track direction of those electrons that, after diffusion

along the track direction,

are contained in a track segment of length l. We write



eff

(

)

(

)

. (7.20)

Figure 7.3 shows how N

eff

(

) varies with diffusion. We have plotted on the ver-

tical axis the quantity

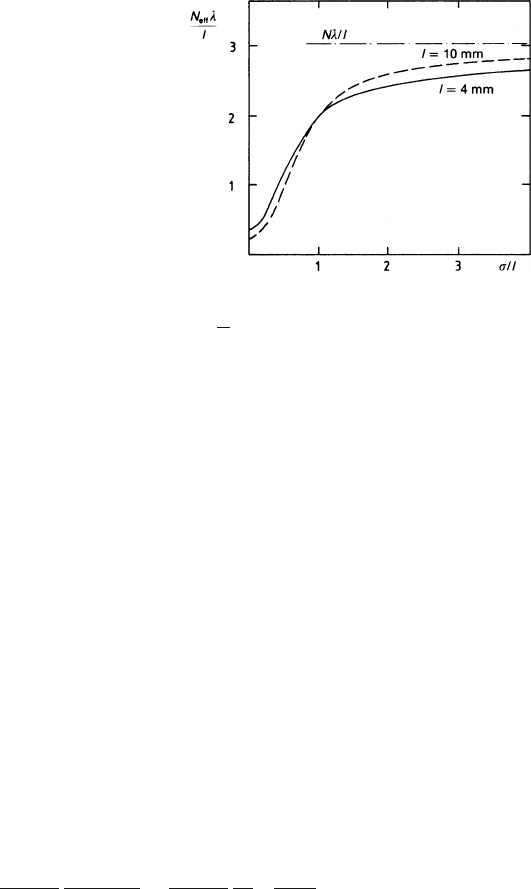
260 7 Coordinate Measurement and Fundamental Limits of Accuracy

Fig. 7.3 Declustering

through diffusion: effective

number of electrons divided

by the total number of

clusters, as a function of

/l,

for two values of l.Inthe

Monte Carlo calculation the

cluster-size distribution of

Fig. 1.7 and a value of

= 2.7 clusters/mm were

used

eff

(

)

where the ratio

/l is equal to the average number of clusters on the track segment

l (

was deﬁned in Sect. 1.1.1 as the mean distance between two clusters). There-

fore N

eff

(

)

/l is the ratio of the effective number of electrons over the number of

clusters in the track length l.

On the horizontal scale we have the diffusion expressed in units of the length

of the track segment

/l. This is suggested by (7.81) and is a very natural choice

because the change of N

eff

(

) is caused by electrons that have diffused so much

that they cross over from one track segment to the neighbouring one, thus breaking

the cluster correlation. It can therefore be expected that N

eff

(

) goes up when

ex-

ceeds some distance comparable to the length of the track segment, i.e. the distance

between the wires. And this is in fact what we see.

The curves in Fig. 7.3 where computed using the argon cluster-size distribution

of Fig. 1.7. At zero diffusion N

eff

(0) is only 0.3(l = 0.4cm) or 0.2 (l = 1cm) of

the number of clusters. We know from Fig. 1.19 that this number must go down

with increasing l. Now we switch on the diffusion, and before

has reached half

the length l of the segment, N

eff

(

) is as large as the number of clusters. For very

large

/l all the clustering is destroyed by the diffusion, and N

eff

(

) approaches the

total number N of electrons. The increase of N

eff

(

) with

/l was ﬁrst observed in

a TPC and termed declustering through diffusion [BLU 86].

We notice that the wire angular term in (7.19) can be written in the following

way:

eff

(

)

(btan

)

eff

(

)



cos



sin

. (7.21)

It represents the variance of the average of the position along the track direction of

the electrons sampled by the wire, projected onto the wire direction. The ﬁrst term

is the variance of a ﬂat distribution of width b/cos

, which is the length of the track

segment sampled by the wire. The factor sin

projects this variance onto the wire

direction.

After this discussion of N



eff

as contained in the second term of (7.19), we deal

now with the ﬁrst term. The simple form into which we have cast the terms directly

7.3 Accuracy in the Measurement of the Coordinate 261

proportional to

(cf. (7.81)) hides the complications in the symbol N



. Although it

is true that in the limiting cases of (7.17) and (7.18) N



is exactly equal to N, the total

number of electrons on the track segment delimited by the cell width, N



changes

as a function of

and b so as to make the variance

larger. The physical

cause of this is the rare larger clusters outside the cell that send some electrons via

diffusion to the edge of the cell, and more so when

is large. We have two reasons

not to go into these details here. When we omit the primes in (7.19) the omissions

amount to less than 25% in the quantity

(except in extreme cases). The omitted

parts, which pull measurements to one side in our cell, have a tendency to pull the

corresponding measurement in the neighbouring cell to the opposite side. Therefore

it is better to leave them out when combining several cells. The contributions of

several wires are discussed in Sects. 7.3 and 7.4.

In conclusion we simplify (7.19) to read

cos

eff

tan

. (7.22)

It represents the square of the accuracy with which a track coordinate X

(7.10)

can be measured along a single wire in the absence of a magnetic ﬁeld.

7.3 Accuracy in the Measurement of the Coordinate

in or near the Wire Direction

7.3.1 Inclusion of a Magnetic Field Perpendicular to the Wire

Direction: the Wire E ×

× B Effect

Drift chambers with precise measurements of the track coordinates along the wire

direction are often operated with a magnetic ﬁeld perpendicular to the direction of

the wires. With this conﬁguration one can obtain a precise determination of the cur-

vature induced on the particle trajectory by the magnetic ﬁeld, and the momentum

of the particle can be determined (see Chap. 8 for details).

The presence of a magnetic ﬁeld perpendicular to the wire direction modiﬁes the

angular wire term of the variance of the arrival position of the electrons (7.5). It

becomes asymmetric and, on average, larger because the track segment is projected

onto the wire in a more complicated way. The electrons that after their drift are

collected in the cylindrical ﬁeld of the wire have to move transverse to the magnetic

ﬁeld (Fig. 7.4). This produces an E ×B force according to (2.6) and causes the

electrons to drift under an effective angle

toward the wire. The angle

is such

that tan

ωτ

, where

is the cyclotron frequency and

is the time between two

electron collisions suitably averaged. Details have been treated in Sect. 2.1.

The arrival position x

of an electron entering the region close to the wire

with coordinates x and y is x

= x −ytan

; the variance of x

on the frequency

distribution (7.3) is

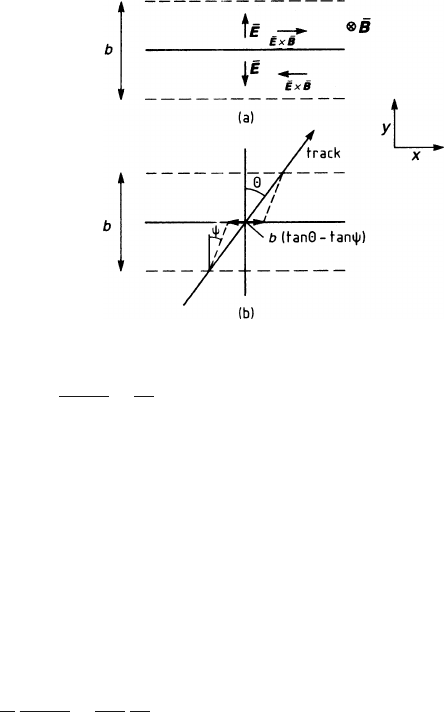
262 7 Coordinate Measurement and Fundamental Limits of Accuracy

Fig. 7.4 (a) Directions of the

electric and magnetic ﬁelds in

the region close to the sense

wire. The magnetic ﬁeld

points into the page. (b)

Direction of the drift velocity

of the electrons in this region

projected onto the x–y plane

x

−x



cos

(tan

−tan

)

. (7.23)

The electrons produced by a track at

= 0 are spread over a region btan

, and

those of a track at an arbitrary angle are smeared over a distance b(tan

−tan

The width of the charge distribution on the wire has a minimum at

and not at

= 0.

This effect was discovered with the TRIUMF-TPC [HAR 84] and is typically the

most important limitation of the measuring accuracy in all TPC-like detectors using

a gas with high values of

ωτ

. In the TRIUMF-TPC the angle

was 29

◦

, and 32

◦

the ALEPH TPC in standard running conditions. The broadening of the avalanche

width has been systematically studied in [BLU 86].

Using (7.23) we can rewrite (7.22) to include this effect:

cos

eff

(tan

−tan

)

. (7.24)

Equation (7.24) is the general expression for the accuracy

with which a

track segment can be measured on one wire along the wire direction. Summa-

rizing our ﬁndings up to here, we see that this accuracy depends on the pro-

jected angle

the track has with respect to the normal to the wire direction as

well as on the angle

of the wire E ×B effect. N

eff

is roughly 6 for 1 cm of

argon NTP and is more accurately obtained in Figs. 7.3 and 1.19. The diffu-

sion term is characterized by the width

of the single-electron diffusion trans-

verse to the drift and the total number N of electrons, typically 100/cm in argon

NTP.

The size and relative importance of the two terms in (7.24) depend on the electron

drift length L, because

is proportional to L and N

eff

depends on L through the

declustering effect (Fig. 7.3). Also the angle

has some inﬂuence on N and N

eff

the length of the track segment varies with

. If one wants to be more speciﬁc, one

has to take into account the details of a particular chamber.

7.3 Accuracy in the Measurement of the Coordinate 263

7.3.2 Case Study of the Explicit Dependence of the Resolution

on L and θ

Writing (7.24) in the form



bcos

(tan

tan

)

cos

g(L)



(7.25)

we have introduced the L dependence of the diffusion and of N

eff

= C

L , (7.26)

eff

= Ng(L) , (7.27)

as well as the

dependence of N:

N = n

b/cos

. (7.28)

Here n

is the number of collected electrons per unit track length. (We recall

that g(L) is not a universal function but depends to some extent on N, b

and

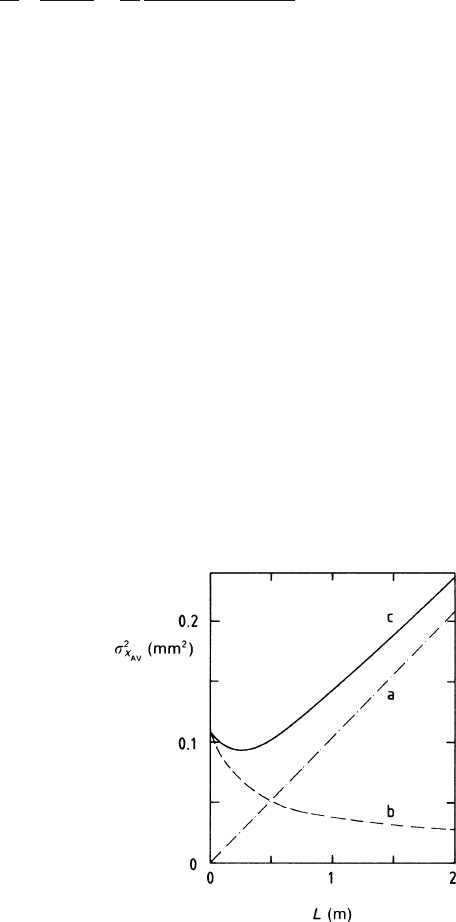
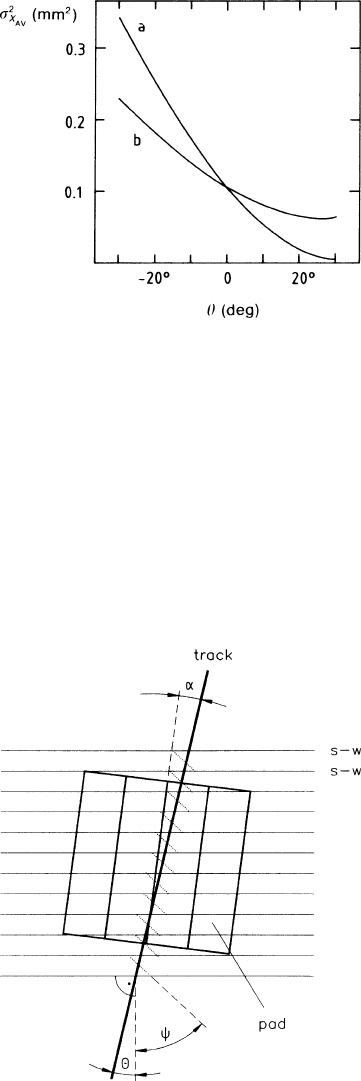
Figure 7.5a-c shows

calculated as a function of L at

= 0forC

= 3.4 ×

−3

mm,

= 32

◦

(corresponding to a gas mixture of 80% argon and 20% methane

in a ﬁeld of 0.85 T), b = 4mm, n

= 8.1electrons/mm. We notice that the resolu-

tion goes through a shallow minimum at small L and is dominated by diffusion at

large L.

Figure 7.6 shows

as a function of the angle

for two different values of L

and for the same choice of the other parameters.

Fig. 7.5a-c Variance of the

average arrival position as a

function of the drift length at

= 0 – the special case

described in the text. (a)

Contribution of the diffusion;

(b) contribution of the

angular wire effect; (c) sum

of the two

264 7 Coordinate Measurement and Fundamental Limits of Accuracy

Fig. 7.6 Variance of the

average arrival position of the

electrons as a function of the

angle

– the special case

described in the text.

(a)L = 0, (b)L = 50cm

7.3.3 The General Situation – Contributions of Several Wires,

and the Angular Pad Effect

The most general situation is the one where the coordinate direction along the pad

row is inclined with respect to the wire direction, and several wires are located op-

posite the same cathode strips, as seen in Fig. 7.7. Apart from

, the angle between

the track and the wire normal, and

, the effective angle of approach caused by the

wire E ×B effect, we also have

, the angle between the normal to the direction of

the pad row and the track; all angles are measured in the wire plane. The angles

and

are the same when the pad row follows the wire direction.

Fig. 7.7 Scheme of a

chamber with cathode-strip

readout. The bold lines

indicate the arrival positions

of the electrons on the wire;

the dotted lines indicate the

direction of the drift velocity

in the region close to the

sense wires

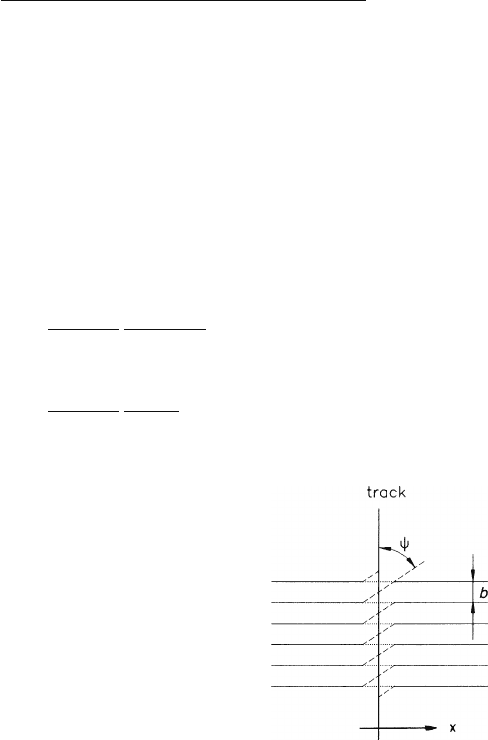
7.3 Accuracy in the Measurement of the Coordinate 265

The signals induced in a cathode strip are from k wires, where

k = pad length h/wire pitch b.

These signals are added in the measuring process. We want to compute the achiev-

able accuracy. As the situation is quite complicated we wish to start with a simple

case. The basic statistical relation will be derived for the special geometry given by

= 0,

= 0; also we will assume

= 0. Later on we will generalize our ﬁndings

step by step.

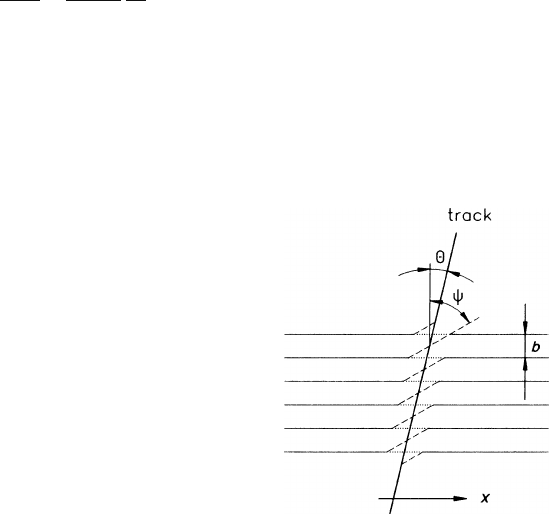
The simpliﬁed geometry is sketched in Fig. 7.8. The ionization clusters along the

track are redistributed onto the sense wires, where they occupy sections of length

btan

. The situation is quite similar to the one in Sect. 1.2.6, where we treated the

problem of charge localization along a track. The coordinate to be determined by

the pads in one measurement is

AV P

∑

i=1

∑

i=m

+ ...+

∑

i=m

k−1

∑

i=1

, (7.29)

where each x

is the position of a cluster with n

electrons; there are m

clusters

on the ﬁrst, and m

−m

j−1

on the jth sense wire ( j = 1,...,k). Averaging over the

positions x

– which are distributed between −(b/2)tan

and +(b/2)tan

–we

ﬁnd for the average and the variance

X

AV P

 = 0

and

AV P

−X

AV P



tan

∑

i=1

∑

i=1

(7.30)

AV P

tan

eff

(h)

(

= 0) .

Fig. 7.8 Track and sense

wires for (7.30)

266 7 Coordinate Measurement and Fundamental Limits of Accuracy

Here we have denoted by 1/N

eff

(h) the statistical factor which is equal to the sum

of the squared cluster size divided by the square of the summed cluster sizes, taken

over all the clusters on the piece of track that is delimited by the pad length h. Let us

repeat (cf. Sect. 1.2.9 that the effective number N

eff

is a measure of ﬂuctuation which

is smaller than the number of clusters because of the ﬂuctuations of the cluster size.

It is not proportional to h; for argon it scales according to Fig. 1.22. Comparing

eff

(b), the corresponding number that belongs to a wire cell, we have for that case

eff

(h) ∼N

eff

(b)(h/b)

0.54

For this reason the achievable accuracy of pads does not improve with the square

root but (for argon) more with the fourth root of the pad length.

In the next step we let

and

be different from zero, but keep

b and

= 0.

The geometry is sketched in Fig. 7.9. The angle

the track makes with the wire nor-

mal has two consequences: it changes the length on the wire occupied by charges,

from b tan

to b(tan

−tan

), and it introduces the projection factor cos

be-

tween this length and the coordinate direction. The diffusion, ﬁnally, contributes to

the variance the same term as in (7.22) but with two changes. Firstly, the projection

factor onto the coordinate direction is 1 in the present case. Secondly, N now repre-

sents the total number of electrons from the track segment delimited by h; we write

N(h), which is of course proportional to h. The variance of X

AV P

therefore assumes

the form

AV P

N(h)

eff

(h)

(tan

−tan

)

cos

(

= 0,

 b). (7.31)

Next we let

assume a non-zero value. This has the consequence that the two

projection factors must be referred to the new coordinate direction, that is the dif-

fusion term receives in its denominator the factor cos

, and the projection factor

of the angular term changes into cos

(

−

). The variance (7.31) of X

AV P

receives

another contribution, which describes the ﬂuctuation of the position of the centre of

Fig. 7.9 Track and sense

wires for (7.31)

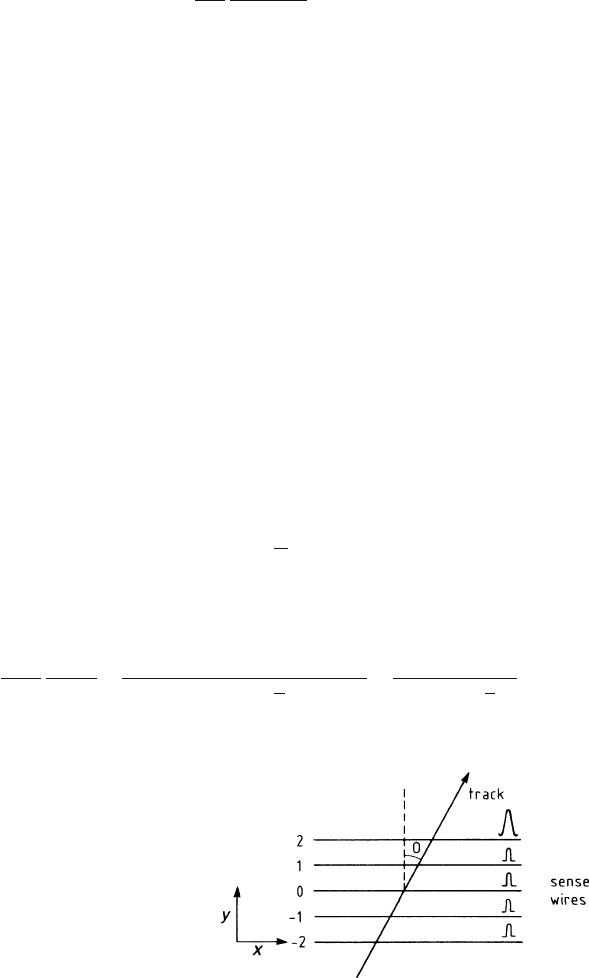
7.3 Accuracy in the Measurement of the Coordinate 267

charge along the track segment, because a non-zero angle

projects this ﬂuctuation

onto the coordinate direction. The size of this term is proportional to the squared

length of the pad,

eff

(htan

)

. (7.32)

This is the angular pad effect. We recognize the similarity with the corresponding

angular wire term in (7.22); in (7.32) the ﬂuctuation is controlled by the effective

number of electrons on the track segment deﬁned by the pad.

This contribution to the variance can be suppressed if the pulse height on the

relevant wires is recorded, because one way of looking at this ﬂuctuation is that it

is caused by the differences in the charge deposited on the wires (see Fig. 7.10).

It has been demonstrated in practice [AME 83, BAR 82], that the measured track

position can be corrected using the wire pulse heights, leaving only a small residual

error.

Finally we have to lift the restriction that

should be small compared to b

In order for declustering to occur, the diffusion must reach the value of a length

parameter which reorganizes the charges in such a way that the cluster correlation is

broken, thus making N

eff

larger. For the angular terms in (7.22) and (7.24) it was b

that set the scale whereas in the angular pad term (7.32) it is h that sets the scale. (It

is irrelevant on which wire the charge is collected – only new charges from outside

the pad region improve the cluster statistics.)

Although the declustering effect often does not play a decisive role in practical

drift chambers – because the diffusion is not large enough – we want to be speciﬁc

in distinguishing the respective scales of the declustering.

For this purpose we denote by

eff





the effective number of electrons on the track segment delimited by h and declus-

tered by diffusion on the scale b. In this sense the variance of X

AV P

takes the form

AV P

N(h)

cos

(tan

−tan

)

cos

(

−

)

12N

eff

−b

)tan

12N

eff

. (7.33)

Fig. 7.10 Displacement of

the measured coordinate

owing to charge ﬂuctuations

between the sense wires that

contribute to a pad signal.

The large pulse height

collected by wire 2 moves the

centroid towards positive x