Blum W., Riegler W., Rolandi L. Particle Detection with Drift Chambers

Подождите немного. Документ загружается.

6.3 Noise and Optimum Filters 217

Z(s)

(s)

V(s)

Z(s)

V(s)

= Z(s)I(s)

(s)V(s)

Linear

Active

Network

Fig. 6.30 Illustration of Thevenin’s and Norton’s theorems

calculated by the well known network rules. The voltage V

(s) and current I

(s)

are related by V

(s)=Z(s)I

(s). As an example we use the circuit of Fig. 6.29.

By shorting the voltage source and opening the current source, the impedance

of the entire network becomes Z(s)=Z

(s)Z

(s)/(Z

(s)+Z

(s)). The Thevenin

equivalent voltage is given by V

(s) from Eq. (6.85) and the current is therefore

(s)=V (s)/Z(s)=I(s)+V(s)/Z(s). The same is true for noise sources: the entire

network can again be represented by a single impedance Z(s) with a series volt-

age noise power spectrum w

( f ) or a parallel current noise power spectrum w

( f )

(Fig. 6.31), and the two are related by

( f )=|Z(i2

f )|

( f ) . (6.87)

Thus we can represent the wire chamber electrode connected to an ampliﬁer

input by a single impedance element Z(s) with a parallel current source representing

the chamber signal and a parallel current noise power spectrum representing all

electrode noise sources (Fig. 6.32).

In this way we can evaluate the relative magnitudes of signal and noise at the

ampliﬁer input, which allows us to choose the ampliﬁer transfer function in order to

optimize the signal-to-noise ratio at the ampliﬁer output.

6.3.2 Noise Sources

Having the vocabulary and the tools for noise analysis at hand we can now discuss

the different noise sources in a wire chamber setup. We consider only the noise in-

herent in the detector and the ampliﬁer and not external ‘man-made’ noise that may

originate in various electrical devices outside of the detector. Of course, any such

interference noise has to be eliminated before approaching the inherent ‘irreducible’

detector and ampliﬁer noise.

Z(s)

(f)

Z(s)

(f)=

(f)

Linear

Network

with noise

sources

(f)

|Z(i2πf)|

(f)

Fig. 6.31 Thevenin’s and Norton’s theorems applied to the noise power spectra

218 6 Electronics for Drift Chambers

Z(s) w

(f) I(s)

Fig. 6.32 Representation of the wire chamber elements, noise sources, and the chamber signal by

a single impedance Z(s) with a single current source and a single noise power spectrum

There are many physical processes that create noise in electric circuits. The three

most important ones for particle detection are shot noise, thermal (Johnson) noise,

and ﬂicker (1/ f ) noise.

Shot Noise

This electrical noise is based on the random arrival of the smallest quantized units

of electric charge. The name derives from an analogy with the pellets of a shotgun.

If the random sequence is governed by the arrival probability p per unit of time

alone (no correlations) one easily calculates the mean number

m of particles in an

observation time T as well as the variance,

−m

m = pT (6.88)

The actual integer number m is distributed around this mean according to the Pois-

son probability distribution

m,m)=

−m

. (6.89)

The expectation value of m

is therefore

∞

∑

m=0

−m

= m+ m

. (6.90)

It follows that the variance is equal to the mean, a famous property of the Poisson

distribution. A power spectrum for this kind of noise exists once an electrical pulse

f (t) is associated with each noise particle carrying the elementary charge e

.We

have a random sequence of identical current pulses coming at a mean frequency

Campbell’s theorem applies [RIC 44]. It states that under these circumstances the

average current

I and its variance

are given by

I =



∞

−∞

f (t)dt



∞

−∞

f (t)

dt. (6.91)

Applying Parseval’s theorem we can transform the expression for

into

= 2



∞

|F(i

df. (6.92)

6.3 Noise and Optimum Filters 219

This can be identiﬁed with the noise power spectrum, which has the following form:

w( f )=2

|F(i

. (6.93)

We note that the power spectrum of shot noise depends on the size of the elementary

charge. For a given current

the ﬂuctuation increases with the size of e

If we imagine f (t) to be a

-function

(t) we have F(i

)=1 and the noise

power spectrum becomes white:

w( f )=2

= 2e

I. (6.94)

This means that we can imagine white noise to be a random sequence of delta current

pulses.

Thermal or Johnson Noise

In 1906 Einstein predicted that Brownian motion of the charge carriers would lead

to a ﬂuctuating potential between the ends of any resistance in thermal equilibrium.

The effect was ﬁrst observed by Johnson [JOH 28] and its power spectrum was

calculated by Nyquist [NYQ 28].

One way to establish the voltage and current ﬂuctuations at the ends of the con-

ductor is to sum up the contributions of the electrons that move about in thermal

equilibrium with the constituents of the conductor. Every electron moving with a

velocity u

down the conductor contributes a small current e

; this is related to

the mean energy per degree of freedom, proportional to the absolute temperature

and the resistance of the conductor. Such a microscopic derivation can be found in

[KIT 58].

A more general derivation of the noise power spectrum follows. It is based on

the insight that the electric and magnetic ﬁelds created by the movements of the

electrons themselves possess degrees of freedom of the system which are in thermal

equilibrium with their surroundings and therefore must carry the average energy

of kT/2 per degree of freedom or kT per mode of the electromagnetic ﬁeld (k =

Boltzmann constant, T = absolute temperature).

In order to ﬁnd the noise power spectrum, all that remains to be done is to prop-

erly count the modes of the electric and magnetic ﬁelds. This was achieved by

Nyquist [NYQ 28] in a paper immediately following the paper in which Johnson

[JOH 28] ﬁrst described thermal noise. One considers two equal resistors R

= R connected by an ideal lossless transmission line as indicated in Fig. 6.33.

The transmission line is given an impedance equal to R, the resistors are in ther-

mal equilibrium at the absolute temperature T . The voltage ﬂuctuations at R

are

accompanied by current ﬂuctuations so that some electrical power P

is ﬂowing

into the line at R

and is being absorbed in R

. There are no reﬂections because

the line is properly terminated. An equal amount of power ﬂows from R

through

the transmission line into R

. The amount of P

can be connected to the vibrational

modes of the transmission line in the following way: Let L be its length and c the

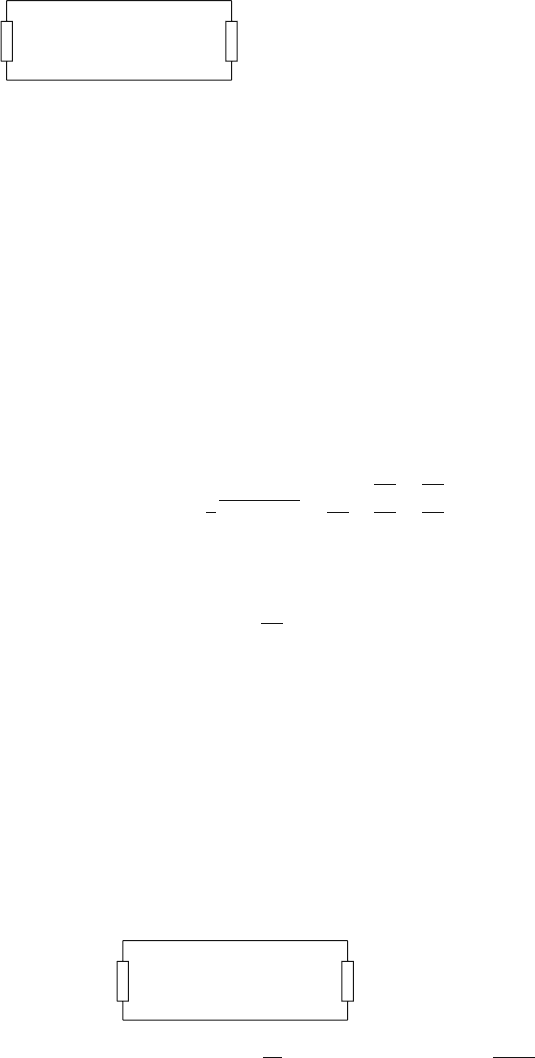
220 6 Electronics for Drift Chambers

Fig. 6.33 Nyquist’s idealized arrangement of two resistors in thermal equilibrium, connected by a

lossless transmission line that has no thermal properties

velocity of propagation of the electrical signals on the line. Let the line suddenly be

isolated from the resistors by short-circuiting both ends so that the electromagnetic

waves are trapped and their modes can be counted. The nth mode has a wavelength

= 2L/n and a frequency f

= nc/2

, so in the frequency interval df there are

2L/cdf modes (n 1), each of which carries an average energy kT.

One half of this energy is the power emitted from R

during the time interval L/c,

so this power is equal to

kT d f (6.95)

in the frequency interval df. It is remarkable that the power density is independent

of f , R

, and the nature of the resistance.

If one wants to express the emitted power P

of one resistor in terms of the ﬂuc-

tuation of the voltage V

(t), one may calculate the total power dissipated in the two

resistors as

2P =

)I =





(6.96)

using I(t)=1/2(V

(t)+V

(t)/2R plus the fact that V

and V

ﬂuctuate incoherently.

Therefore, using Eq. (6.96), we ﬁnd that the voltage ﬂuctuations per frequency unit

across a resistor is

= 4kTR. (6.97)

One says that the voltage noise power spectrum is

w( f )df = 4kTRd f , (6.98)

where w( f ) is expressed in V

/Hz [cf. Eq. (6.79)]. As it is independent of f it is

‘white’ noise.

Next we have to consider the temperature noise originating from a passive net-

work described by a complex impedance. Let the resistance R be connected to such

a network with impedance Z( f )=R( f )+iX( f ), according to Fig. 6.34 By reason-

ing according to Nyquist, as above, we know that the power transferred from the

Z(iω) = R(ω) + iX(ω)

Fig. 6.34 Resistance R and network with impedance R( f )+iX( f ) on the same temperature,

connected to each other. The noise at R is

; the noise from the network is V( f )

6.3 Noise and Optimum Filters 221

resistance to the network is equal to that transferred in the opposite direction. The

former is seen by simple circuit theory to be equal to

R( f )

(R + R( f ))

+ X( f )

df (6.99)

and the latter is simply equal to

V( f )

(R + R( f ))

+ X( f )

df. (6.100)

We therefore have to conclude that the voltage power spectrum of any passive net-

work is

( f )df = 4R( f )kTd f = 4kT Re[Z(i

)]df. (6.101)

The equivalent parallel current noise spectrum is

( f )df =

( f )

|Z(i

= 4kT Re[1/Z(i

)]df. (6.102)

Following upon Planck’s work, we see that Eq. (6.95 ff) are only valid as long as

the average energy of one mode of the electromagnetic ﬁeld is much higher than the

quantum energy hf at frequency f (where h is Planck’s constant). This is actually

the case for all our electronics applications. Under quantum conditions, i.e., for

temperatures and frequencies where kT becomes comparable to hf, instead of (6.95)

the average energy becomes

exp(hf/kT) −1

per mode of the electromagnetic ﬁeld (6.103)

which approaches kT when kT  hf.

Flicker or 1/f Noise

There is a third category characterized by increasing noise with decreasing fre-

quency. It is not one single well-deﬁned process that causes it but rather a whole

collection, sometimes not completely understood. This ‘ﬂicker noise’ typically oc-

curs in non-equilibrium situations in devices subjected to applied bias voltage to

which it is often proportional. Examples are the contact resistance ﬂuctuations in

carbon microphones and carbon resistors or leakage currents in the dielectric of ca-

pacitors. It occurs in ﬁeld effect transistors and in many other places discussed in

the literature [ROB 74].

The frequency dependence of the power spectrum is often near 1/ f and may

extend to very low f (on the order of 10

−2

Hz or less). It is well known that a single

relaxation process (one governed by an exponential decrease in the time response)

cannot account for the observations, but perhaps a superposition of several would

222 6 Electronics for Drift Chambers

serve. One way to parametrize the power spectrum w( f ) is to specify the frequency

at which the ﬂicker noise is equal to the white temperature noise power w

( f )=

4kRT d f. The total power spectrum is then

tot

( f )=w

( f )(1+ f

/ f ) . (6.104)

The value of f

has been seen to differ from as low as 10

−2

Hz to as high as

100 MHz, but it is usually in the region of a few kHz [ROB 74]. For practical

purposes active electronic circuit components often carry a speciﬁcation from the

manufacturer.

Ampliﬁer Noise

When dealing with signals it is sufﬁcient to represent the ampliﬁer only by its

transfer function W (s) and input impedance Z

(s), without referring to the spe-

ciﬁc realization. However, the noise output signal of an ampliﬁer depends on the

speciﬁc components of the ampliﬁer circuit and the noise analysis is generally quite

a complex task.

It is possible to represent the effect of all the noise sources inside an ampliﬁer

by two noise generators at the input of the device, which is treated as a noise-free

black box [MOT 93]. If the noise generators are correlated there is in addition a

complex correlation coefﬁcient; this we may neglect here because the noise sources

are typically quite independent.

Figure 6.35 shows this model, where a voltage noise generator w

( f ) and a

current noise generator w

( f ) are placed at the input of the noiseless ampliﬁer. Tra-

ditionally the voltage and current noise power spectra of the ampliﬁer are called

( f )=e

( f ) and w

( f )=i

( f ). We call e

( f ) the series noise power spectrum

and i

( f ) the parallel noise power spectrum of the ampliﬁer. This provides a com-

plete representation of all the internal ampliﬁer noise sources. The voltage and

the current noise generators must be dealt with separately because their relative

importance depends on the impedance of the signal source. Once this in known

they may be contracted in a single noise generator. This is our procedure in what

follows.

(f) = e

(f)

(s)w

(f) = i

(f)

Fig. 6.35 Ampliﬁer noise model, where the noise is formulated by a pair of noise sources at the

input of a noiseless device. The voltage noise generator w

( f )=e

( f ) and current noise generator

( f )=i

( f ) provide a complete representation of the numerous noise sources inside the real

ampliﬁer

6.3 Noise and Optimum Filters 223

In order to calculate the noise power spectra e

( f ) and i

( f ) one must of

course analyze the entire ampliﬁer circuit. Although the numerous elements of the

ampliﬁer all contribute to the noise, it is typically only the ﬁrst element of the circuit

(ﬁrst transistor or feedback resistor) that dominates the noise. The thermal noise,

shot noise, and 1/ f noise of this ﬁrst element deﬁnes the noise performance of the

ampliﬁer. Bipolar transistors or ﬁeld effect transistors are the classical basic build-

ing blocks for detector readout electronics. In semiconductor devices incorporating

a p-n junction, the charge carriers interact with ﬁelds due to applied external volt-

ages only in the depletion layer at the junction, which is a region that is distinct

from the region where their statistical properties are established. Bipolar transistors

are therefore typical shot-noise-limited devices. The noise power spectra are then

given combinations of 2e

,2e

, and 2e

where I

are the collector, base,

and emitter currents.

If the interaction region with the external ﬁelds coincides with the region where

the carrier ﬂuctuations are generated and the carriers remain approximately in ther-

mal equilibrium during their interaction, the thermal (Johnson) noise will dominate.

Field effect transistors, where the ﬂuctuations are established in the channel, are

typical thermal-noise-limited devices [ROB 74]. The 1/ f noises of bipolar and ﬁeld

effect transistors show characteristic differences which have to be considered in the

choice of electronics technology.

However, the purpose of our discussion is not the design of the ampliﬁer but

rather it is the other way around. By comparing the wire chamber signal and

the noise due to the passive components of the wire chamber with the ampliﬁer

noise at the input of the ampliﬁer we can deﬁne the acceptable magnitudes of the

ampliﬁer noise. This procedure results in a speciﬁcation for acceptable ampliﬁer

noise.

Because the shot noise and thermal noise are white noise sources we can deﬁne

an equivalent noise resistance R, where w

= 4kTR at T = 295K gives a power

spectrum equal to the one from the input transistor. Although the parallel noise i

and series noise i

can both show 1/ f noise, we limit ourselves to the following

ampliﬁer noise spectra:

( f )

= 4kTR

+ B/(2

f ) i

( f )=4kT/R

. (6.105)

The series noise resistance R

, the parallel noise resistance R

, and ﬂicker noise

coefﬁcient B specify the noise behaviour of the ampliﬁer at a given working point.

Noise in a Readout Channel, Electrode+

+Ampliﬁer

We now have all the ingredients necessary to calculate the noise levels for a readout

channel of a wire chamber. We connect the detector model from Fig. 6.32 to the

ampliﬁer model from Fig. 6.35 and perform one ﬁnal simpliﬁcation: The voltage

noise source e

can be transformed into a current noise source by using Eq. (6.87),

and the resulting current noise sources can be contracted into one; the resulting

power spectrum assumes the form

224 6 Electronics for Drift Chambers

(f)

Z(s) Z(s)

(s)

gH(s)

I(s) w(f)I(s)

(s)

Fig. 6.36 All noise sources collected into a single current noise source at the ampliﬁer input. This

is our universal model for the ensemble of chamber signal source plus ampliﬁer

w( f )=w

( f )+i

( f )+

( f )

|Z(i

. (6.106)

The current noise spectrum w( f ) is called equivalent input noise. We thus have

represented the entire readout channel by the chamber impedance Z(s), the par-

allel current noise density w( f ), the ampliﬁer input impedance Z

(s), and the

chamber signal I(s) (cf. Fig. 6.36). Note that w( f ) is independent of the ampli-

ﬁer’s gain and its input impedance. It is this property that makes the equivalent

input noise the most useful index upon which to compare the noise characteris-

tics of various ampliﬁers and devices. Summarizing the previous section, we note

that the noise components of Eq. (6.106) are as follows: The thermal chamber

noise w

( f ) is caused by the dissipative elements in the wire chamber through

(

)=4kT Re[1/Z(i

)]. The ampliﬁer noise is represented by the parallel noise

resistance R

, the series noise resistance R

, and the coefﬁcient for the 1/ f

noise:

)=4kTRe



Z(i

)



4kT

4kTR

+ B/

|Z(i

. (6.107)

The ampliﬁer input impedance Z

(s) enters when we calculate the signal and

noise at the output of the ampliﬁer. The fraction of current ﬂowing into the ampliﬁer

is Z/(Z + Z

), so the chamber current signal and the noise current ﬂowing into the

ampliﬁer are

(s)=

Z(s)

Z(s)+Z

(s)

I(s) w

( f )=

|Z(i

)+Z

w( f ). (6.108)

Finally, the ampliﬁer output signal V (s) and the variance of the ampliﬁer output

noise

are

V(s)=gH(s)I

(s)



∞

(

|H(i

. (6.109)

In the following we use these results to discuss the three most important elec-

trode conﬁgurations: cathode readout, wire readout, and a terminated transmission

line channel. We want to see their behaviour for both a bipolar and a unipolar

shaper.

6.3 Noise and Optimum Filters 225

6.3.3 Noise in Wire Chambers

Cathode Channel

This case is relatively simple because Z(s) is given only by the chamber capacitance

, and the parameters of the universal model are

Z(s)=

I(s)=I

ind

(s) w

(

)=4kTRe[1/Z(i

)] = 0. (6.110)

The capacitor C

is not a source of noise because it contains no dissipative elements.

The equivalent input noise deﬁned in Eq. (6.107) is therefore given by

w( f )=

4kT

+ 4kTR

+ B

. (6.111)

For the readout electronics we take the unipolar and bipolar shapers H

uni

(s) and

bip

(s) from Sect. 6.2 and an ampliﬁer input impedance Z

= R

that is neg-

ligible compared to the detector impedance Z. We thus assume that |Z(i

)| =

 R

. This is a good approximation for f  1/2

, which for a

typical ampliﬁer input resistance of 50

and a detector capacitance of 20 pF eval-

uates to f  200MHz. We set Z

= 0 for Eq. (6.108) and have I

(s)=I(s) and

(

)=w(

Now we can calculate the ampliﬁer output noise according to Eq. (6.109). We

ﬁrst need the expression |H(i

for the unipolar and the bipolar shapers. H(i

) is

the Fourier transform of the normalized delta response; it was speciﬁed in Eq. (6.37)

and depends on the number of stages that make up the shaping circuit (cf. Fig. 6.13);

is the peaking time of both the unipolar and the bipolar shaper. We obtain

uni

n!)

)

]

n+1

bip

n!)

)

]

n+1

, (6.112)

where r = n −

√

n as the peaking times are the same. The integration over all fre-

quencies for

leads to integrals of the form



/(a

+ b

)

n+1

, which can be

written in closed form as



∞

+ b

)

n+1

dx =

2n−2k+1

2k+1

n!4

(2k)!

(2n −2k)!

(n −k)!



∞

2k+1

+ b

)

n+1

dx =

2n−2k

2k+2

k!(n −k −1)!

(6.113)

The variance of the ampliﬁer output noise is then



∞



4kT

+ 4kTR

+ B



|gH(i

, (6.114)

226 6 Electronics for Drift Chambers

(f)

Z(s)

(s)

gH(s)

ind

(s) w(f)I(s)

(s)

Fig. 6.37 Cathode pad connected to to an ampliﬁer and the universal model of the readout channel

which ﬁnally evaluates to



4kT



4kTR

= ENC

. (6.115)

and K

are dimensionless parameters given by

Unipolar Bipolar





(2n −1)!

(2r)

r(2n −2)!





(2n −2)!

(2r)

(n −1)(2n −4)!





n!(n −1)!

(n −1)!(n −2)!

(6.116)

These parameters are of the order of unity and they are shown in Fig. 6.38. The

noise r.m.s. is written as

= gENC, where ENC is the so-called equivalent noise

charge.

We saw earlier that injecting a delta current Q

(t) into an ampliﬁer of sensitivity

g results in an ampliﬁer output pulse height of V = gQ. Therefore, injecting a delta

signal with charge Q = ENC into the ampliﬁer results in an output pulse height

equal to the r.m.s of the ampliﬁer output noise. The ENC characterizes the noise

level independently of the ampliﬁer sensitivity g and is the most useful quantity for

comparing the noise behaviour of different ampliﬁers.

Fig. 6.38 The parameters K

,andK

for the unipolar

and the bipolar shaper

represented as continuous

functions of n, the number of

stages. For n = 4theylie

between 0.5 and 1.5

3 4 5 6 7 8

0.5

1.5

2.5

(bip)

(unip)