Blake A.J.(ed.) Crystal Structure Analysis

Подождите немного. Документ загружается.

202 Analysis of extended inorganic structures

1.45

1.46

1.47

1.48

1.49

1.50

1.51

1.52

1.53

1.54

1.55

1.56

1.57

1.58

1.59

1.60

1.61

1.62

1.63

1.64

1.65

P-O Distance (Å)

Number of distances

1.55

1.59

1.63

1.67

1.71

1.75

1.79

1.83

1.87

1.91

1.95

1.99

2.03

2.07

2.11

2.15

2.19

2.23

2.27

2.31

2.35

Mo-O Distance (Å)

Number of distances

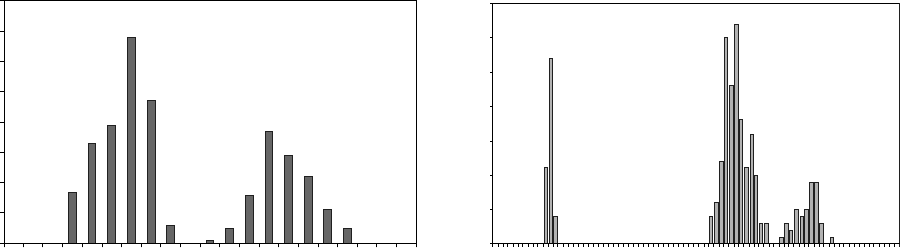
Fig. 14.11 Histograms of bond lengths for PO

tetrahedra and MoO

octahedra.

within expected ranges [minimum, maximum and average values for

the 3 atom types were: 42×Mo 0.0051–0.0062, average =0.0056 Å

;

84×P 0.0049–0.0068, average = 0.0058 Å

; 315 × O 0.0069–0.0170, aver-

age =0.0097 Å

]. Bond valence sums for the 42 MoO

octahedra and

84 PO

tetrahedra deviated by < 0.15 units (3%) from expected values.

With 42 MoO

octahedra in the structure one would expect 42 ‘short’

Mo–O bonds, 168 ‘medium’ Mo–O bonds and 42 ‘long’ Mo–O bonds.

For the 84 PO

tetrahedra that link to form P

units one would expect

210 short P–O bonds and 126 longer P–O–P bonds. The histograms in

Fig. 14.11 show exactly this distribution!

References

Allen, F. H. (2002). Acta Crystallogr. A58, 380–388.

Attﬁeld, J. P., Kharlanov, A. L. and McAllister, J. A. (1998). Nature 394,

157–159.

Brese, N. E. and O’Keeffe, M. (1991). Acta Crystallogr. B47, 192–197.

Brown, I. D. and Altermatt, D. (1985). Acta Crystallogr. B41, 245–247.

Costentin, G., Leclaire, A., Borel, M. M., Grandin, A. and Raveau, B.

(1992). Z. Kristallogr. 201, 53–58.

Egami, T. and Billinge, S. (2003). Underneath the Bragg peaks: structural

analysis and complex materials. Pergamon Press, Oxford, UK.

Huang, H. F. and Sleight, A. W. (1992). J. Solid State Chem. 100, 170–178.

Neder, B. and Proffen, T. (2008). Diffuse scatter and defect structure

simulations. Oxford University Press, Oxford, UK.

Proffen, T., Neder, R. B. and Billinge, S. J. L. (2001). J. Appl. Crystallogr.

34, 767–770.

Radosavljevic, I. and Sleight, A. W. (2000). J. Solid State Chem. 149,

143–148.

Shannon, R. D. (1976). Acta Crystallogr. A32, 751–767.

Exercises 203

Exercises

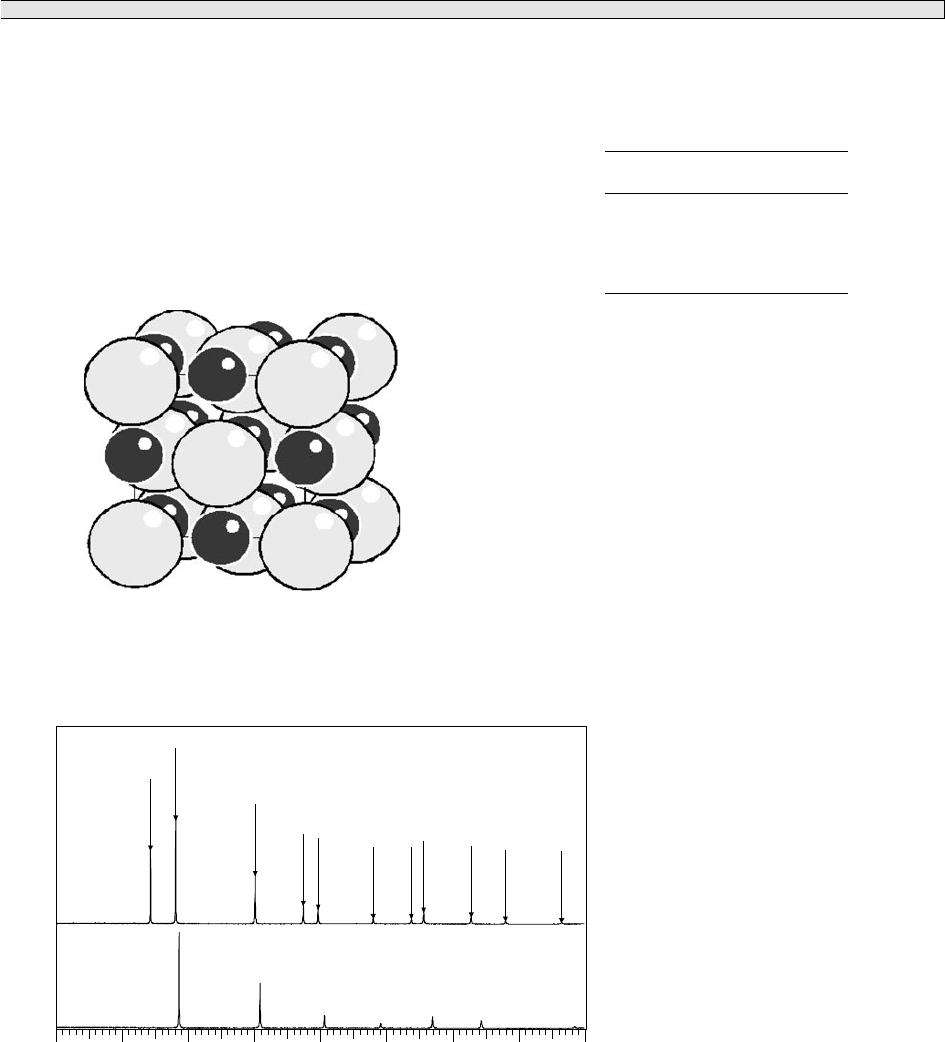
1. As partof anundergraduatepracticalclass astudent was

asked to record powder diffraction patterns of the com-

pounds BaS and SrSe, both of which have the rock salt

structure (Fig. 14.12). Ionic radii (Å) are Ba 1.49, Sr 1.32,

S 1.70, Se 1.84. Unfortunately the student has forgotten

to label the patterns (which are shown in Fig. 14.13). Can

you help?

Fig. 14.12 Rock salt structure.

Table 14.3 Literature coordinates

of MnRe

xyz

Mn1 0 0 0

Re1

3 0.2891

O1 0.135 0.349 0.206

3 0.57

2. The structure of MnRe

has been described in space

group P

3 with unit cell parameters a = b = 5.8579,

c = 6.0665 Å and fractional co-ordinates as shown

in Table 14.3. Draw a plan view of the structure and

determine the co-ordination environment of Mn and Re

atoms. Given bond distances of 2.179 Å for Mn1–O1,

1.704 Å for both Re1–O1 and Re1–O2 and R

values

of 1.79 and 1.97 Å for Mn

/Re

VII

, determine bond

valence sums for Mn and Re. Do you think this struc-

ture is correct? What error could have been made when

solving/reﬁning the structure?

3. As described incase history 2, the structure of Mo

was originally described using an incorrect unit cell with

a = 8.3065, b = 6.5154, c = 10.7102 Å , β = 106.695

◦

V = 555.20Å

.Fromtheinformation belowcalculate the

Intensity

2-theta

10 20 30 40 50 60 70 80 90

d = 3.67 084

d = 3.17920

d = 2.24856

d = 1.91752

d = 1.8355 8

d = 1.58954

d = 1.4588 9

d = 1.4219 0

d = 1.29799

d = 1.22 397

d = 1.12414

Fig. 14.13 Powder diffraction patterns of BaS and SrSe.

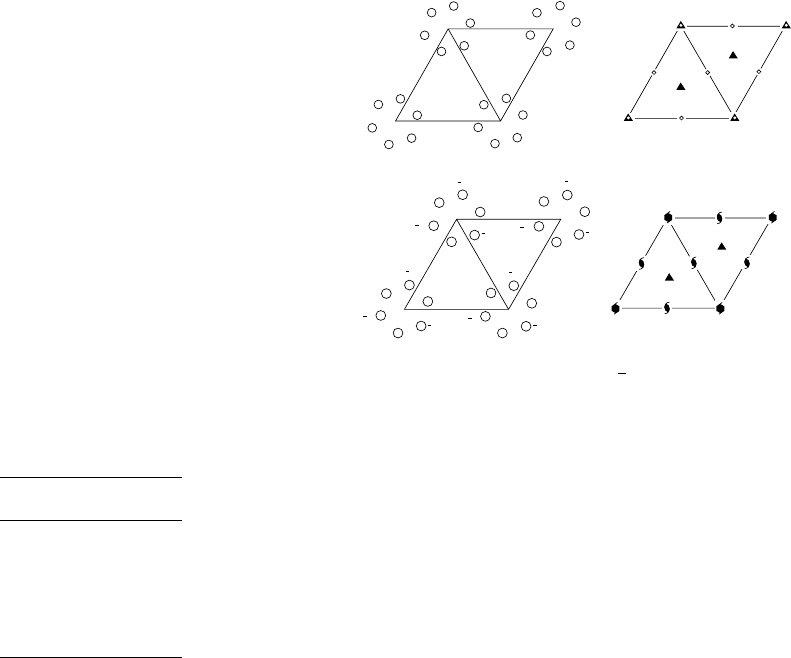
204 Analysis of extended inorganic structures

transformation matrix required to convert to the correct

cell. Calculate the volume of the true cell.

Strong Supercell Reflections

-3 -3 1 d = 5.0378 2-th = 17.5904 I = 352.05 sigI = 7.90

-2 3 -4 d = 4.0281 2-th = 22.0493 I = 965.51 sigI = 28.70

4 6 -6 d = 2.4436 2-th = 36.7491 I = 152.14 sigI = 4.46

Selected Subcell Reflections

0 0 2 d = 5.1294 2-th = 17.2739 I = 154.96 sigI = 6.38

-1 -1 0 d = 5.0531 2-th = 17.5367 I = 2356.06 sigI = 15.64

-1 0 2 d = 5.0172 2-th = 17.6633 I = 392.77 sigI = 2.91

-2 0 1 d = 4.1308 2-th = 21.4946 I = 1.98 sigI = 0.25

0 1 -2 d = 4.0365 2-th = 22.0030 I = 6739.94 sigI = 17.90

-1 1 2 d = 3.9811 2-th = 22.3129 I = 1233.35 sigI = 5.97

-3 0 3 d = 2.4669 2-th = 36.3908 I = 0.55 sigI = 0.30

3 1 0 d = 2.4580 2-th = 36.5273 I = 1989.42 sigI = 11.78

2 2 -2 d = 2.4507 2-th = 36.6401 I = 1048.92 sigI = 9.43

3 0 1 d = 2.4059 2-th = 37.3473 I = 0.11 sigI = 0.29

4. A layered form of SiP

containing corner-linked SiO

octahedra and P

tetrahedra has been described in

space group P6

with a = 4.7158, c = 11.917 Å and

fractional co-ordinates as shown in Table 14.4. Sketch

Table 14.4 Literature co-

ordinates of SiP

xyz

Si1 0 0 0

3 0.394

3 0.133

O1 0.859 0.178 0.100

3 0.261

O3 0.93 0.261 0.422

–

Fig. 14.14 Symmetry elements for P3 (top) and P6

(bottom).

Reproduced from International Tables for Crystallography, Vol. A,

with permission of the International Union of Crystallography.

the structure. Bond distances are 3×Si–O1 1.768 Å,

3×Si–O2 1.701 Å, 3×P2–O1 1.476 Å, P2–O2 1.525 Å,

P1–O2 1.585 Å and 3×P1–O3 1.481 Å. Do you think

this structure is correct? See Fig. 14.14 for space group

symmetry.

5. RbMn[Cr(CN)

].xH

O is a framework material related

to the Prussian Blues. What methods would you use to

probe its structure? What are the potential problems of

each approach?

The derivation of results

Simon Parsons and William Clegg

15.1 Introduction

The parameters obtained from the least-squares reﬁnement are a set

of co-ordinates and displacement parameters for each atom, and from

these we are able to calculate geometrical parameters of interest: bond

lengths, bond angles, torsion angles, least-squares planes with angles

between them, intermolecular and other non-bonded distances. We can

analyze the movement of the atoms and, perhaps, make some correc-

tions to the apparent geometrical values we have calculated. To every

derived result we can attach a standard uncertainty as a measure of its

precision or reliability.

We must begin to interpret the results, to detect patterns, common

features, signiﬁcant differences and variations, and to make deductions

on the basis of the observed geometry. We shall need to compare fea-

tures within the structure, and also compare them with other related

structures.

15.2 Geometry calculations

So now we have a converged reﬁnement with which we are satisﬁed.

The primary results include three co-ordinates for each atom. The sec-

ondary results, generally of greater interest, are parameters describing

the molecular geometry.

15.2.1 Fractional and Cartesian co-ordinates

The positions of atoms in least-squares reﬁnement are (almost) always

expressed as fractional atomic co-ordinates. Familiar formulae for the

calculation of distances, angles, etc., assume, however, that the co-

ordinates are referred to Cartesian axes. One approach to calculating

geometric parameters from crystallographic data is to transform the

fractional coordinates into Cartesian co-ordinates. In order to do this the

Cartesian frame (deﬁned by vectors X, Y and Z) must be deﬁned in terms

of the crystallographic unit cell axes (a, b and c). There are an inﬁnite

number of ways in which this can be done, but one common deﬁnition

is to allow the Cartesian X-axis to lie along the crystallographic a-axis

205

206 The derivation of results

and the Cartesian Y-axis to lie in the crystallographic ab-plane, perpen-

dicular to X. The Cartesian Z-axis is then parallel to c* (more generally it

is given by the vector product X × Y). The matrix relationship between

these two sets of axes is

⎛

⎝

⎞

⎠

⎛

⎜

⎝

−1

a tan γ

b sin γ

∗

cos β

∗

cos α

∗

⎞

⎟

⎠

⎛

⎝

⎞

⎠

= M

⎛

⎝

⎞

⎠

. (15.1)

Note that −1/a tan γ = 0ifγ = 90

◦

. The inverse operation is

⎛

⎝

⎞

⎠

⎛

⎜

⎝

a 00

b cos γ b sin γ 0

c cos β

−c(cos β cos γ − cos α)

sin γ

c∗

⎞

⎟

⎠

⎛

⎝

⎞

⎠

= M

−1

⎛

⎝

⎞

⎠

(15.2)

For transformation of co-ordinates between Cartesian and fractional

systems the following apply (T indicates the transpose of a matrix):

⎛

⎝

cart

⎞

⎠

= (M

−1

)

⎛

⎝

frac

⎞

⎠

(15.3)

⎛

⎝

frac

⎞

⎠

= M

⎛

⎝

cart

⎞

⎠

. (15.4)

The following relationships are included for reference (V = volume):

∗

bc sin α

∗

ac sin β

∗

ab sin γ

cos α

∗

cos β cos γ − cos α

sin β sin γ

cos β

∗

cos α cos γ − cos β

sin α sin γ

cos γ

∗

cos α cos β −cos γ

sin α sin β

V = abc(1 −cos

α − cos

β − cos

β + 2 cos α cos β cos γ)

∗

(15.5)

15.2 Geometry calculations 207

Once a set of Cartesian co-ordinates has been derived ordinary Carte-

sian geometry can be applied to calculations of distances, angles and

so on. Cartesian co-ordinates are also useful when making comparisons

of structures, or as a common co-ordinate framework for superposition

calculations.

15.2.2 Bond distance and angle calculations

An alternative method for calculating geometric parameters, which is

frequently more computationally convenient, is to apply vector meth-

ods directly to fractional co-ordinates themselves. Suppose we have

two atoms with fractional co-ordinates [x

, y

, z

] and [x

, y

, z

]; the

interatomic vector will be:

r =[(x

− x

)a + (y

− y

)b + (z

− z

)c]. (15.6)

The length (magnitude) of this vector can be evaluated from its dot

product with itself:

|r|

= r.r =[(x

− x

)a + (y

− y

)b + (z

− z

)c]

. [(x

− x

)a + (y

− y

)b + (z

− z

)c]

= (ax)

+ (by)

+ (cz)

+ 2bc cos αyz

+ 2ac cos βxz + 2ab cos γxy. (15.7)

Bond angles, θ , can also be evaluated from dot products: if two

interaction vectors u and v are represented as in (15.6), then

u.v =|u||v|cos θ . (15.8)

Alternatively, for three atoms A–B–C the angle θ is also given by the

‘cosine rule’

cos θ =

+ r

− r

. (15.9)

Torsion angles measure the conformational twist about a series of four

atoms bonded together in sequence in a chain A–B–C–D. The torsion

angle is deﬁned as the rotation about the B–C bond that is required

to bring B–A into coincidence with C–D when viewed from B to C. The

generally accepted sign convention is that a positive torsion angle corre-

sponds to a clockwise rotation. Regrettably, this convention is opposite

to that used to deﬁne positive rotations elsewhere in geometry. Note

that (i) the torsion angle D–C–B–A is identical in magnitude and sign to

the torsion angle A–B–C–D, so there is no ambiguity in the description

of the angle; (ii) the torsion angles for equivalent sets of atoms in a pair

of enantiomers have equal magnitudes but opposite signs, so that all

torsion angles change sign if a structure is inverted. Formulae for the

calculation of torsion angles are given by Dunitz (1979).

208 The derivation of results

15.2.3 Dot products

The dot product r.r in (15.7) is conveniently expressed in matrix

format as:



x y z



⎛

⎝

a.aa.ba.c

b.ab.bb.c

c.ac.bc.c

⎞

⎠

⎛

⎝

x

y

z

⎞

⎠



x y z



⎛

⎝

x

y

z

⎞

⎠

. (15.10)

Note that G is symmetric because b.c = c.b, and that it can be evaluated

from the cell dimensions because b.c = bc cos α, etc. The matrix G is

called the metric tensor, and is extremely important. An equivalent recip-

rocal metric tensor can be deﬁned using the reciprocallattice basis vectors,

and this is usually given the symbol G

∗

. The following relationships are

often useful:

−1

= G

∗

(15.11)

V =|G|

1/2

(15.12)

∗

=|G

∗

1/2

. (15.13)

The metric tensors transform between direct and reciprocal space:

⎛

⎝

∗

⎞

⎠

= G

∗

⎛

⎝

⎞

⎠

⎛

⎝

⎞

⎠

= G

⎛

⎝

∗

⎞

⎠

(15.14)

The above formulae are very useful in computer programs, and pro-

vide a much more memorable means for evaluation of volumes and

reciprocal lattice constants than the explicit formulae presented in (15.5).

15.2.4 Transforming co-ordinates

Fractional co-ordinates (x, y, z) correspond to vectors of the form

r = xa + yb + zc,

which can be written in matrix format as



abc



⎛

⎝

⎞

⎠

= A

x. (15.15)

15.2 Geometry calculations 209

Suppose we wish to transform our unit cell using a 3 ×3 matrix R from

the A-basis to another basis, B, where

B = RA.

This may be because we wish to model the structure in a different space

group, or to compare one structure with another. It will be clear that we

also need to transform our co-ordinates, x, to another set, y.

The same vector r can now be expressed in two ways:

r = A

r = B

so that

x = B

But B = RA, and so

x = (RA)

Recalling that (AB)

= B

x = A

x = R





−1

x = y,

(15.16)

which is the desired relationship: if a unit cell is transformed with a

matrix R, the co-ordinates should be transformed with(R

)

−1

= (R

−1

)

Thisexplains why the transformations used in(15.1)and(15.2) arediffer-

ent from those used in (15.3) and (15.4). The same matrix R used to trans-

form the direct cell axes can also be used to transform reﬂection indices.

15.2.5 Standard uncertainties

Although the occasional distance or angle can be calculated by hand

(for example, where a non-bonded distance is required, but is not listed

automatically by the reﬁnement program because it is too long), these

derivations are tedious, and are best left to automatic computer pro-

grams. Even more to the point, the correct calculation of s.u.s for the

molecular geometry parameters requires inclusion of covariance terms

(see Chapter 16), because atomic co-ordinates are not uncorrelated; the

necessary covariances, produced automatically by a full-matrix least-

squares reﬁnement (note: reﬁnements not based on a full matrix do not

give all the covariances, and also tend to underestimate variances), are

210 The derivation of results

not normally preserved and output after the reﬁnement, so only approx-

imate s.u.s can be calculated using parameter s.u.s alone. The approxi-

mationwill be a particularlypoorone when symmetry-equivalent atoms

are involved, e.g. for a bond across an inversion centre, or an angle at

an atom on a mirror plane.

Note that any parameter that is varied in the least-squares reﬁne-

ment will have an associated s.u., and any parameter that is held ﬁxed

will not. Usually, the three co-ordinates and six anisotropic U

(or one

isotropic U) for each atom are reﬁned, and each has an s.u. Symmetry

may, however, require that some parameters are ﬁxed, because atoms

lie on rotation axes, mirror planes or inversion centres; in this case, the

s.u. of such a ﬁxed parameter must be zero. This has an effect on the

s.u.s of bond lengths and other geometry involving these atoms, which

will tend to be smaller than they would be for reﬁned parameters. If

a co-ordinate of an atom has been ﬁxed in order to deﬁne a ﬂoating

origin in a space group with a polar axis (better methods are used in

most modern programs), the effect will be to produce artiﬁcially better

precision for the geometry around this atom.

Parameters that are equal by symmetry must have equal s.u.s. This

applies both to the primary reﬁned parameters (for example, atoms in

certain special positions in high-symmetry space groups have two or

more equal co-ordinates and relationships among some of the U

com-

ponents), and also to the geometrical parameters calculated from them.

A good test of the correctness of the calculation of geometry s.u.s by

a program is to compare the bond lengths and their s.u.s for atoms in

special positions in trigonal and hexagonal space groups!

If a bond length (or other geometrical feature) has been constrained

during reﬁnement, the s.u. of this bond length must necessarily be zero,

even though the two atoms concerned will, in general, have non-zero

s.u.s for their co-ordinates; this is a consequence of correlation: the

covariance terms exactly cancel the variance terms in calculating the

bond length s.u. from the co-ordinate s.u.s. A good example of such a

situation is the ‘riding model’ for reﬁnement of hydrogen atoms, where

theC–H bond is held constant in length and direction during reﬁnement.

The C and H atoms have the same s.u.s for their co-ordinates (because

they are completely correlated), and the C–H bond length has a zero s.u.

By contrast, restrained bond lengths do have an s.u., because the restraint

is treated as an extra observation and the two atoms are actually reﬁned

normally. It is instructive to compare the calculated bond length and its

s.u. with the imposed restraint value and its weight, to see how valid

the restraint is in the light of the diffraction data.

For a group of atoms reﬁned as a ‘rigid group’, all internal geometrical

parameters will have zero s.u.s. The actually reﬁned parameters are the

threeco-ordinates for some deﬁned point in the group (usually one atom

or the centroid) and three rotations for the group as a whole. Thus, dif-

ferent atoms in the group should have different co-ordinate s.u.s (this

is not the case with some reﬁnement programs, which do not calcu-

late these s.u.s correctly), and, once again, the effects of correlation and

15.3 Least-squares planes and dihedral angles 211

covariance are such as to give the required zero s.u.s for the geometry

of the group.

It is often overlooked that molecular geometry depends not only on

the atomic co-ordinates, but also on the unit cell parameters, and they

too are subject to uncertainties. Some reﬁnement programs make no

allowance for the uncertainties in the cell parameters, and the results

can be ridiculous, especially for the geometry around heavy atoms.

These usually have very low co-ordinate s.u. values, so bond lengths

and angles calculated without regard to cell parameter uncertainties

may have s.u.s proportionately very much smaller than the cell edge

s.u.s! If explicit treatment of this effect is not included in your geometry

calculation program, a simple hand adjustment can be made, by increas-

ing s.u.s by an amount depending on the ratio of the cell edges to their

s.u.s [σ(a)/a, σ(b)/b and σ(c)/c]; this usually affects only the heaviest

atoms in a structure of contrasting atomic scattering powers.

15.2.6 Assessing signiﬁcant differences

In crystallography we quote the standard uncertainty in parentheses,

for example 1.520(4) Å, for a bond length. The ﬁgure in parentheses

refers to the last quoted decimal place, and in this example the standard

uncertainty on our measurement of 1.520 Å is 0.004 Å; a measurement

of 1.52(4) Å is ten times less precise. See also Chapter 16 for further

discussion.

Application of arguments based on the normal distribution allows us

toconclude that twoparameterscan beconsideredsigniﬁcantlydifferent

if their difference () is more than 3 times the standard uncertainty of

the difference, i.e.





+ σ

≥ 3, (15.17)

whereσ

isthe s.u. on the ﬁrst parameter. This is called the ‘3σ rule’, but it

is important to recognize that the s.u.s from crystal-structure reﬁnement

are often thought to be underestimated by a factor of 1.5 to 2, and so

perhaps a 5σ rule is safer to use in practice.

15.3 Least-squares planes and

dihedral angles

It is sometimes desirable to assess whether a number of atoms are actu-

ally all in one plane and, if not, how much they deviate from coplanarity;

this is particularly the case for cyclic groups of atoms and for selected

atoms co-ordinating a central metal atom. When more than one exact

or approximate plane can be deﬁned in a structure, the angles between

pairs of planes may also be of interest.