Blake A.J.(ed.) Crystal Structure Analysis

Подождите немного. Документ загружается.

222 Random and systematic errors

At this stage we should also distinguish carefully between precision

and accuracy. The accuracy of an experiment is a measure of how close

the result is to its true value. The precision is a measure of the repro-

ducibility of a result and therefore of how conﬁdently the result can be

deﬁned. Truly random errors affect the precision but not the accuracy of

measurements and results. Depending on their exact nature, systematic

errors may or may not affect precision, but they do affect accuracy, and

so high precision is not of itself an indication of a ‘good’ result.

The precision of a measured quantity can be expressed by its standard

uncertainty, s.u. (alsocalled its standarddeviation or estimated standard

deviation, e.s.d.). In crystallography we quote the standard uncertainty

in parentheses, for example 1.520(4) Å for a bond length. The ﬁgure in

parentheses refers to the last quoted decimal place, and in this example

the standard uncertainty on our measurement of 1.520 Å is 0.004 Å; a

measurement of 1.52(4) Å is ten times less precise. Instead of 1.520(4) we

might have written 1.520 ± 0.004 Å, but this is an unfortunate notation

as it appears to specify a strict range for the bond length. While this

is what engineers do mean by this notation, the correct interpretation

in crystallography, and the physical sciences generally, is rather more

subtle.

Randomerrorscanbe treatedbystatistical analysis of howtheseerrors

aredistributed about zero,and this is why probability distributions have

assumed such importance in crystallography. Systematic errors can not

be treated by such a general theory, and each source of error must be

identiﬁed and its effect modelled by consideration of its physical nature.

16.2 Random errors and distributions

16.2.1 Measurement errors

The existence of random error means that whenever we make a

measurement of a quantity, x, what we actually measure is

= x

true

+ ε

where, in the absence of systematic errors, x

true

is the true, accurate,

value of x, andε

is a random measurementerror. If we were to measure x

again, our measurement would be slightly differentbecause the random

error ε

would not be the same as when we made our ﬁrst measurement.

We can never know x

true

, but we can estimate its value, and obtain

some idea of the quality of our estimate. We do this by making multiple

measurements of x, and applying statistics.

16.2.2 Describing data

Consider the data below, which are the F

values measured for equiv-

alents of the 114 reﬂection of N

taken directly from an hkl data ﬁle

16.2 Random errors and distributions 223

after application of an absorption correction. N

is is cubic (space

group Im

3), and the redundancy is unusually high (N = 67).

INTENSITIES OF THE 114 REFLECTION. N=67

1684.78 1787.27 1794.81 1807.33 1819.65 1825.30 1853.30

1743.72 1788.16 1796.12 1807.53 1819.81 1826.18 1854.28

1756.32 1788.23 1798.56 1807.54 1819.88 1827.00 1856.05

1761.98 1788.50 1801.34 1808.86 1820.28 1830.38 1867.75

1767.55 1789.60 1802.79 1812.50 1821.31 1830.85 1872.35

1767.86 1789.69 1804.08 1813.05 1821.57 1832.63 1881.82

1772.06 1793.45 1804.38 1813.05 1822.44 1834.59 1902.13

1772.38 1793.93 1804.49 1813.54 1823.11 1836.25 1784.30

1794.50 1804.54 1814.43 1823.32 1837.49 1784.60 1794.52

1804.75 1819.36 1823.51 1841.55

A histogram illustrating these data is given in Fig. 16.1. Notice that,

although the range of F

is 1684 to 1902, most measurements clump

together in the middle of the range, with relatively few at the extremes.

This is a description of the distribution of the data.

In some distributions the individual data can take only certain values:

forexample,the number of photons counted by a detector, or the number

of people in a particular age group, must be integral. A case where the

values that can be taken by members of the distribution are only certain

discrete ones gives rise to a discrete distribution. By contrast, the data that

make up the elements of the distribution in Fig. 16.1 can adopt any value

(e.g. 1684.78 or 1787.27), and this yields a continuous distribution.

1680

Frequency

1720 1760 1800

|F**2| of 114

1840 1880

Fig. 16.1 Histogram showing intensities of the 114 reﬂection, superimposed on a curve

of the corresponding ideal normal distribution (see Section 16.2.3).

224 Random and systematic errors

If we measured all the x

that it is possible to measure, which may

mean making an inﬁnite number of measurements, then we could spec-

ify exactly the form of a distribution. This is called the parent distribution.

In general this is not possible, and the best we can do is to measure a

sample distribution.

The two most important quantities that characterize a distribution are

the mean

x and the variance σ

(the square of the standard deviation). The

mean is what we loosely call the ‘average’ value of the variable, x

, taken

from N different measurements:

x =



i=1

. (16.1)

The symbol μ is also often used for the mean, but it is best to distinguish

between μ for the true (unkown) mean of the complete parent distribu-

tion and

x for the sample mean. In the distribution shown in Fig. 16.1 x

are the individual values of F

, and N(= 67) is the number of reﬂections

in the data set. The variance of the sample distribution is deﬁned as

N −1



i=1

− x)

, (16.2)

and is a measure of the width or spread of the distribution over the

different values of x. The variance is the square of the standard deviation

σ, and σ is often called the sample standard deviation. Equations (16.1) and

(16.2) give our best estimates of the true mean and standard deviation

of a parent distribution based on data taken from a sample distribution.

The term N − 1 appears in (16.2) because calculation of the mean

has removed one degree of freedom from the calculation. It is sometimes

replaced simply by N, though this is strictly correct only for com-

plete distributions and not for sample distributions; on calculators these

alternatives may be designated σ

N−1

and σ

, respectively. Press et al.

(1991) say that if this distinction ever matters to you, then you are prob-

ably up to no good…trying to substantiate a questionable hypothesis with

marginal data.

All observations in a set of repeated measurements will contribute

equally to the mean and standard deviations given in (16.1) and (16.2).

However, it is often the case that individual observations will have some

measure of their precision; for example, values of σ(F

) are available

from counting statistics or proﬁle ﬁtting for each reﬂection in a dataset,

while a set of bond lengths to be averaged will also have a standard

uncertainty calculated after least-squares reﬁnement. In these cases it

may be appropriate to weight the calculation of the mean:



. (16.3)

16.2 Random errors and distributions 225

The standard deviation can be calculated using either:



, (16.4)

N −1



− x)



. (16.5)

The ﬁrst is more common, but in the crystallographic intensity data-

merging program SORTAV, for example, where these quantities are

referred to as σ

ext

and σ

int

, both are calculated and the larger of the

two taken (Blessing, 1997). Choice of weights, w

, has become some-

thing of a subdiscipline of statistics (see Section 16.4), but a common

choice when averaging a set of measurements x

with precision σ(x

) is

to use w

= 1/σ

Other quantities that may be quoted are the median, mode, skewness

and kurtosis (or curtosis) of the data. The median of a sample of data

values is the middle value of the data set when the values are placed in

ascending order. If the sample size is even, then the median is deﬁned as

being half-way between the two middle values. The median is impor-

tant because it is less sensitive to large outliers than the mean. As an

illustration, suppose the set of measurements was made for a particular

quantity: 0.9, 1.1, 1.2, 1.5, 10.0. The value 10.0 is obviously an outlier (a

mistake). The outlier strongly affects the value of the mean: 2.94 with

the outlier, 1.18 without. The median, by contrast is affected much less:

1.2 with the outlier, 1.15 without. This property is called robustness.

Table 16.1. Statistical

descriptors for the intensities

of the 114 reﬂection.

Mean, x 1809.9

Sample standard 32.8

deviation, σ

Median 1808.9

Skew −0.39

Kurtosis 3.02

Number of data 67

The mode is the most common value in a set of data, corresponding

to the maximum in a histogram. The sample skewness is a measure of

the symmetry of a distribution, and the kurtosis measures its peakiness.

Formulae are given in statistics text books [e.g. Barlow (1997), p.14].

Values of the mean, sample standard deviation, median, skewness and

kurtosisfor the datainFig. 16.1 aregiven inTable16.1.The negative skew

means that the data tail off to the left; the kurtosis value is interpreted

below.

The mode, skewness and kurtosis seem to be encountered rather

rarely in crystallography. Indeed Barlow (1997) says: Kurtosis is not used

much by physicists, chemists, or indeed anyone else. It is a really obscure and

arcane quantity whose main use is inspiring awe in demonstrators, professors

or anyone else you are trying to impress.

16.2.3 Theoretical distributions

The shape of the histogram in Fig 16.1 can be described using a math-

ematical function called a probability distribution function,orpdf. There

are many such functions, some familiar ones being the binomial, Pois-

son, normal, and uniform distributions. By far the most important in

226 Random and systematic errors

crystallography (indeed in the physical sciences generally) is the normal

distribution, which is also called the Gaussian distribution.

The mathematical expression for this very important distribution is

P(x; μ, σ) =

√

2π

exp



−

(x − μ)

2σ



, (16.6)

where μ and σ

are the mean and variance, respectively. P(x; μ, σ

) is

the probability of measuring a particular value x given the mean and

variance. The distribution is said to be indexed on the mean and variance.

The distribution is symmetrical about its mean, and the function calcu-

lated with μ = 1809.9 and σ = 32.8 is superimposed on the histogram in

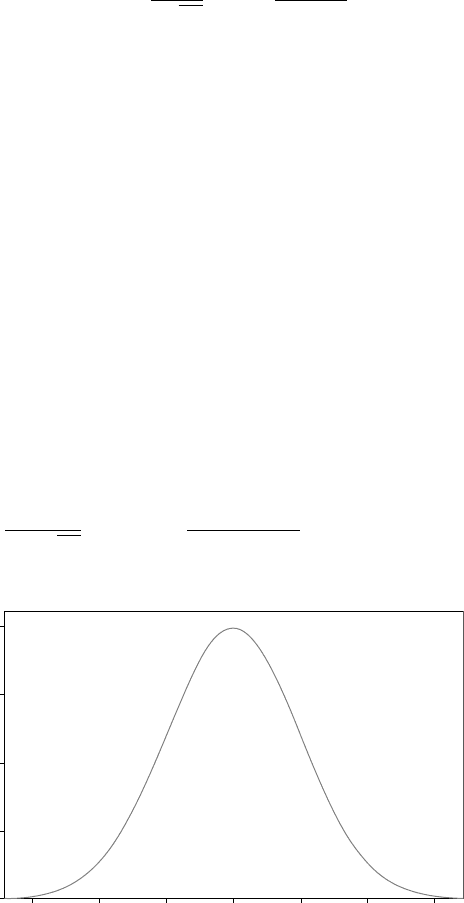
Fig. 16.1. The main characteristics of a normal distribution are shown in

Fig. 16.2. The values of the skew and kurtosis for a normal distribution

are both 0. The fact that the data in Fig. 16.1 have a positive kurtosis

(Table 16.1) means that the data are more sharply peaked than a normal

distribution: they are leptokurtic as opposed to platykurtic.

Equation (16.6) can be used to evaluate the probability of measuring

to be 1801 (say): it is only 0.012. This seems odd at ﬁrst sight, since

from the appearance of the histogram 1801 looks quite likely. But it is

important to recall that we are dealing with a continuous distribution,

and it is more meaningful to evaluate the probability that x lies in a

speciﬁed range x

to x

; this is



P(x)dx. The probability of measuring

between 1798 and 1804 is:

32.8

√

2π

1804



1798

exp



−

(x − 1809.9)

2 × 32.8



dx = 0.070,

–3

0.4

0.3

0.2

0.1

Normal P(X; mu = 0, sigma = 1)

0.0

–2 –1 0 1 2 3

Sigma from mean

Fig. 16.2 The normal distribution calculated with a mean of 0 and a standard deviation

of 1. 68.3% of a normal distribution lies within ±1σ of the mean, and the interval ±3σ

encloses 99.7% of the total distribution.

16.2 Random errors and distributions 227

or 7% [if we measured 100 equivalents we would expect 7 of them to

lie between 1798 and 1804]. Statistics books (e.g. Barlow, 1997, p. 38)

tabulate integrals of the normal distribution within ±(x −μ)/σ from the

mean. 1801 is (1809.9 − 1801)/32.8 = 0.27σ from the mean, and tables

give the probability of measuring a value within 0.27σ of the mean to

be 21.28%. 68.27% of the area under the curve lies between ±1σ, and

99.73% between ±3σ (this forms the basis for the ‘3σ rule’ for assessing

signiﬁcant differences, see Section 15.2.6). Note that the total probability

for all possible values of x is 1:

∞



−∞

P(x)dx = 1. (16.7)

The normal distribution is particularly important because of an effect

expressed by the Central Limit Theorem. Suppose we have a set of N

independent variables x

; each variable belongs to its own population

with mean μ

and variance σ

. The function

y =



i=1

(16.8)

has a distribution that, as N becomes very large, approaches a normal

distribution with mean and variance



i=1

and σ



i=1

, (16.9)

whether the individual variables x have normal distributions or not.

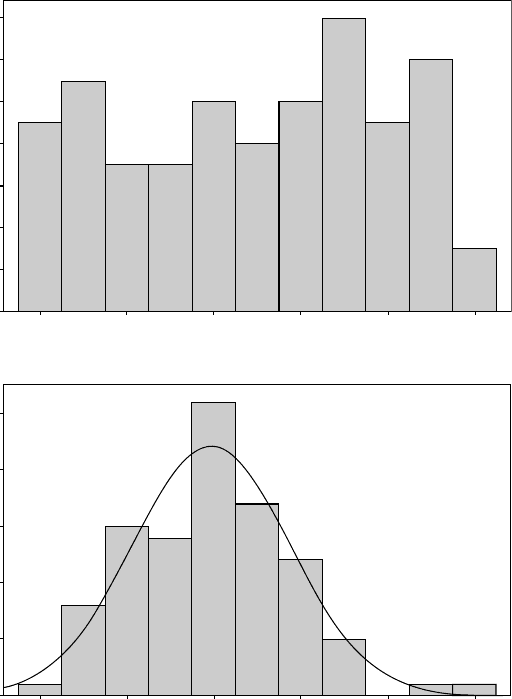
Figure 16.3 shows the central limit theorem in action: the top ﬁgure is a

histogram of 100 random numbers taken from a uniform distribution,

the lower ﬁgure is a histogram of the sum of 10 such sets of random

numbers.Although each of the 10 setsof random numbershas a uniform

distribution their sum has a normal distribution.

It is generally assumed that the experimental determination of the

value of a particular quantity is subject to a large number of independent

sources of small errors. All of these contributing errors are summed

to form the ε

in some measured quantity. Because of the central limit

theorem, the ε

values are normally distributed.

16.2.4 Expectation values

The expectation value, f(x), of any function f(x) can be calculated

provided its pdf, P(x), is known:

f(x)=

∞



−∞

f(x)P(x)dx. (16.10)

228 Random and systematic errors

345

Sum of 10 random numbers

678

0.0 0.2 0.4 0.6 0.8 1.0

Random number (uniform distribution)

FrequencyFrequency

Fig. 16.3 The central limit theorem in action.

The mean of a distribution is the expectation value of x:

x=

∞



−∞

xP(x)dx, (16.11)

and this is equal to μ for a normal distribution. The variance is the

expectation value of (x − μ)

; this is σ

for a normal distribution. The

quantity



∞

−∞

P(x)dx is called the rth moment of a pdf.

Another illustrative example of the use of expectation values is in

the calculation of E-statistics in ideal intensity distributions. For a cen-

trosymmetric structure, Wilson (1948) showed that the values of |E|

16.3 Taking averages 229

follow a normal distribution:

−1

(|E|) =



exp



−|E|



Therefore

|E

− 1| =



∞



− 1|exp



−|E|



dE = 2



exp



−1



= 0.968.

For a non-centrosymmetric structure

(|E|) = 2|E|exp



−|E|



and

|E

− 1| = 2

∞



− 1||E|exp



−|E|



dE =

= 0.736.

Note that the integration limits here are 0 and ∞ as this is the

range of |E|.

16.2.5 The standard error on the mean

Suppose we make N separate measurements of a quantity x. The mea-

sured values x

…x

are a sample from all the possible measurements

we could make, which follow some unknown distribution P(x). For suf-

ﬁciently large N, a consequence of the central limit theorem is that the

mean

x of our N sample values is normally distributed with the same

mean μ as the parent population (all possible measurements) and with

variance

(x) =

. (16.12)

By ‘variance ofthe mean

x’ weunderstand the variance we would obtain

by taking many such samples, calculating the mean

x for each separate

sample, and then looking at the distribution (mean and variance) of

these individual sample means. The factor N in (16.12) means that the

standard error on the mean can become very small for large numbers of

observations, and it is extremely important to question thevalidity of the

assumption that the data are drawn from the same parent distribution.

16.3 Taking averages

The mean and standard deviation can always be calculated from a set of

numbers, such as a set of bond distances, and it is very tempting to do

230 Random and systematic errors

this. Two questions arise: (i) is it better to use (16.1) or (16.3) to calculate

the mean, and (ii) is such an average meaningful?

Taylor and Kennard (1983) showed that a weighted mean (16.3) is

appropriate if the variation in the values to be averaged is mainly due

to experimental random errors, so that the observed values are nor-

mally distributed about their mean. They illustrated their analysis using

twelve C=N bond distances taken from a number of different crystal

structures of adenine derivatives. The distance data were as listed in

Table 16.2.

The weighted mean calculated using (16.3), (16.4) and (16.12) and

= 1/σ

) is 1.314(2) Å. In order to assess whether this is valid we

need to test for normality in the bond-distance data in Table 16.2.

Table 16.2. Bond-distance

data (in Å) for weighted

mean calculation. Taken

from Taylor and Kennard

(1983).

1.315(3) 1.378(29)

1.311(3) 1.325(30)

1.322(12) 1.314(30)

1.329(12) 1.333(32)

1.347(21) 1.294(45)

1.301(23) 1.315(45)

16.3.1 Testing for normality using a histogram

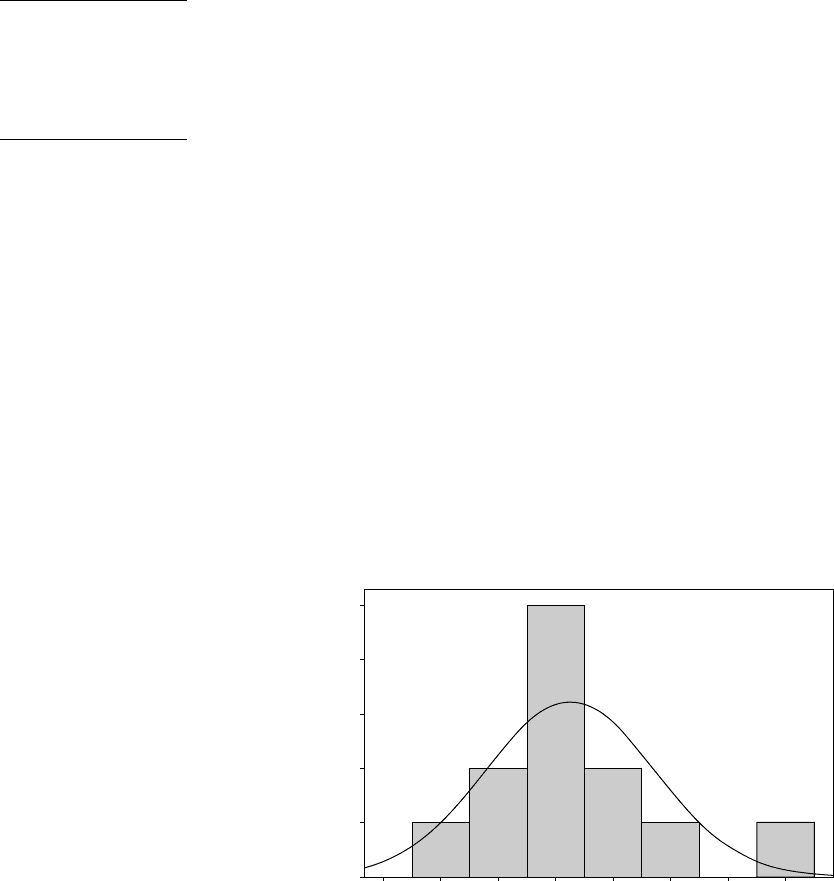
One obvious test for normality is to plot the data and see if the resulting

histogram looks like a normal distribution. Figure 16.4 shows this for

the data in Table 16.2.

There are only 12 data here, but the histogram is highest in the middle

and there is only one maximum, which is what we would expect for

normally distributed data. A more quantitative test is described below.

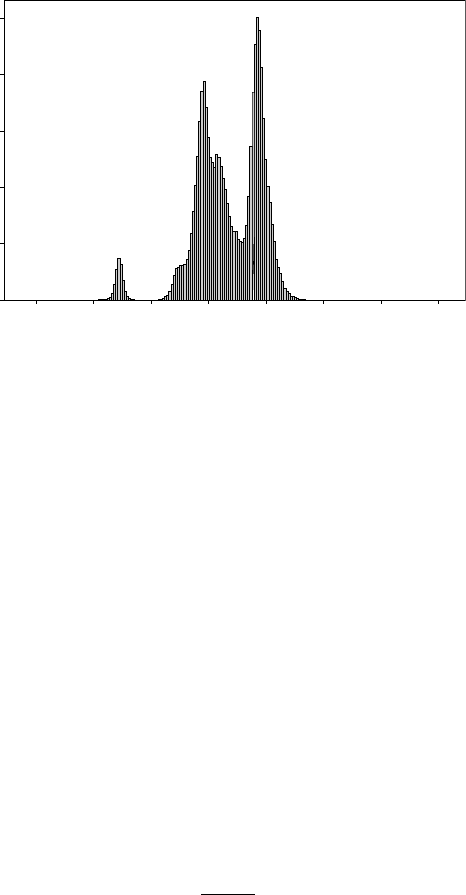
Often, histograms can be multimodal (i.e. have two or more maxima):

in such cases it is meaningless to calculate an average. An extreme exam-

ple is shown in Fig. 16.5, a histogram of all the CN distances in organic

molecules in the Cambridge Structural Database (Allen, 2002). We could

calculate the average of these data to be 1.3967 Å, with a standard error

on the mean of 0.0002 Å. This appears very precise because there are a

lot of CN distances in the CSD (212 914), and so a large number goes

into the denominator of (16.12). This is utterly meaningless because the

1.275

Frequency

1.290 1.305 1.320 1.335

CN Bond length (Å)

1.350 1.365 1.380

Fig. 16.4 Histogram of the data in Table 16.2; a normal distribution pdf has been

superimposed.

16.3 Taking averages 231

0.945

10000

8000

6000

Frequency

4000

2000

1.085 1.215 1.350 1.485 1.620 1.755 1.890

CN distance (Å)

Fig. 16.5 Histogram of CN distances in the CSD.

histogram actually contains data on CN single, double, triple and delo-

calized bonds. It is as though we had an apple and a banana and tried to

determine the average fruit. Just because we can do a calculation does

not guarantee that the result is meaningful.

16.3.2 The χ

test for normality

A more quantitative test for normality is to calculate the value of χ



−

)

, (16.13)

where w

are the weights used to calculate the weighted mean.

The expectation value of χ

is N −P where N is the number of obser-

vations and P is the number of parameters that needed to be determined

from the set of numbers before χ

could be calculated. N −P is referred

to as the number of degrees of freedom, and in the case of determining a

mean, only one parameter, the mean, has hadto be determined, so P = 1.

It is convenient to deﬁne a reduced χ

red

N −P

, (16.14)

which has an expectation value of 1.

For Taylor and Kennard’sdata the value of χ

is 11.66, and the number

of degrees of freedom 12 − 1 = 11, therefore χ

red

= 1.06. The fact that

this is near 1 means that we can conclude that the errors in the data are

normally distributed. In fact we can assign a probability to the previous

statement, and this is discussed in specialist text books on statistics (e.g.

Barlow, 1997; page 150).

The normality of a distribution can also be tested with a normal

probability plot, and this is discussed below in Section 16.4.3.