Blake A.J.(ed.) Crystal Structure Analysis

Подождите немного. Документ загружается.

232 Random and systematic errors

16.3.3 Averaging data when χ

red

 1

When the variation in a sample is mainly due to environmental effects,

such as crystal-packing effects on bond distances, the mean should be

calculated using (16.1). The standard deviation, σ(sample), should be

calculated using (16.2), i.e. the sample standard deviation should be

quoted, not the standard deviation on the mean. Taylor and Kennard

(1983) argue that, if each measurement has its own standard deviation,

it is better to estimate the standard deviation using

= σ

(sample) −

_______

), (16.15)

though the second term (the average variance of the measurements) is

usually so much smaller than the ﬁrst that it makes little difference.

The C=N bond distances in adenine derivatives, for example, appear

to be rather insensitive to crystal-packing forces, and this may be

described as a ‘hard’ geometrical parameter. Other parameters, such as

metal–metal bond lengths in clusters, bond angles, torsion angles, and

intermolecular contact distances, are much more variable and subject to

environmental effects. Such parameters may be described as ‘soft’. It is

important to remember that an average value is meaningless for a set

of parameters that are not really equivalent (i.e. they do not belong to

the same normal distribution). Even for bonds that appear to be chemi-

cally similar, statistical equivalence may not be found. In such cases, it

is better to quote a range of values, but if you feel driven to calculate

an average anyway, use (16.1) for the mean, and σ (sample) (16.2) for its

standard deviation.

16.4 Weighting schemes

Weighting schemes occur throughout crystallographic calculations,

such as merging of data, least-squares reﬁnement, and analysis of

results. In the following section we will discuss the use of weighting

schemes in reﬁnement.

It may seem odd to start discussing least-squares reﬁnement in a

chapter on statistics and errors. However, least squares is one form of

estimation, a technical term used in statistics to refer to the derivation of

numerical quantites from a sample set of data. The mean and standard

deviation are two estimators, and when, for example, intensity data are

merged using (16.3), we are deriving an estimate (using the word in its

technical sense) of the intensity of a reﬂection given a sample set of data.

Least squares is the most important estimation procedure in physical

science.In least squareswe estimate numerical values of parameters from

a dataset, including co-ordinates, displacement parameters, standard

uncertainties etc.). We minimize a quantity



− Y

)



w

, (16.16)

16.4 Weighting schemes 233

where Y = F

or F. Comparison of (16.16) with (16.13) should convince

you of the link that exists between reﬁnement and statistics.

We have already seen that it is important to be sure that data belong

to the same parent distribution before averaging them and calculating

a standard error on the mean. It can also be shown that use of least-

squares formulae implicitly assumes that the measurement errors in Y

are normally distributed (compare (16.16) with the exponent in (16.6)).

This is a fair assumption, because intensity measurements are subject

to many small sources of error, and so the central limit theorem will

make overall errors follow a normal distribution, as required. However,

the central limit theorem works better at the centre of a distribution

than in the tails, and it is common in real datasets to ﬁnd data further

away from the mean than would be expected if real measurement errors

were truly normally distributed. This means that although the w

are

conventionally chosen to be 1/σ

) in data merging and reﬁnement,

the σ

) may not in fact be the best estimates for the errors in our

measurements.

16.4.1 Weights used in least-squares reﬁnement with

single-crystal diffraction data

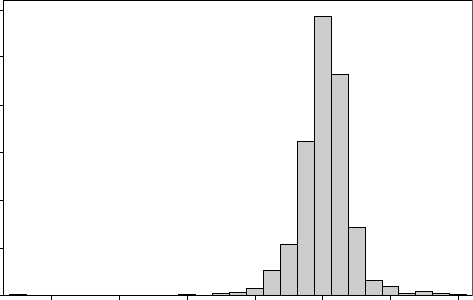
Figure 16.6 shows a histogram of values of (F

− F

)/σ(F

) calculated

after reﬁnement of the crystal structure of serine hydrate. According to

the theory of the normal distribution, if our σs really are a good estimate

of our measurement errors, there should be essentially no data with

|(F

−F

)/σ(F

)| > 3, but in fact there are lots, including some enormous

outliers.

Extraerrorscancome fromuncorrectedsystematicerrors(particularly

absorption and extinction) that are turned into apparent random errors

–32

300

250

200

150

Frequency

100

–24 –16 –8 0 8 16

(Fobs**2–Fcalc**2)/sigma

Fig. 16.6 The variation of (F

−F

)/σ(F

) taken fromthereﬁnementofthecrystal structure

of the amino acid serine hydrate.

234 Random and systematic errors

after merging. Conventional crystallographic models are also incapable

of fully reproducing observed diffraction patterns because of the use

of spherical atom scattering factors and harmonic approximations for

thermal motion (see Section 16.7). If our measurement errors were really

normal we could just weight on σ

). Since they are not, to put no ﬁner

point on it, we ﬁddle the σs!

Oneway to modify the σs isto recognize that the biggest errors(extinc-

tion and absorption) are associated with the strong data, and to increase

the σ

) according to

) + aF

, (16.17)

where a is chosen in such a way as to produce a more satisfactory plot

than that shown in Fig. 16.6 (a is often between 0.1 and 0.01). Crystal-

lographers used to do this until Wilson (1976) showed that using F

like this induced bias in the reﬁned parameters. Use of F

instead also

induced bias but only about half as much and in the opposite sense. To

take account of this, σ

) is changed to σ

) + a(F

+2F

)/3. This is

the basis of the weighting scheme devised by Sheldrick (2008) for use

in SHELXL:

) + (aP)

+ bP

, (16.18)

whereP = (F

+2F

)/3 and a and b are chosen tomake χ

red

constant over

bins of data grouped according to intensity or resolution (a so-called ﬂat

analysis of variance; see Section 16.4.3).

A completely different approach (Carruthers and Watkin, 1979) is to

throw away the σs altogether, and to ﬁt a graph of (Y

− Y

)

versus

to some function. The inverted function then becomes the weighting

scheme, so guaranteeing a ﬂat analysis of variance.

16.4.2 Robust-resistant weighting schemes

and outliers

Although most data in a set of measurements usually have errors that

follow a normal distribution, some data will be poorly measured, and

should be thrown away. Such data appear on their own well away from

the centre of a distribution, and they are referred to as outliers. An exam-

ple of such an outlier is the intensity measurement of 1684 in Fig. 16.1.

We saw above that aberrant data points can affect the value mean.

They can also seriously affect parameter estimates in least-squares

reﬁnement. The mean and least-squares calculations are said not to be

robust, and it is important therefore to remove outliers from crystallo-

graphic procedures such as merging and reﬁnement.

One method for identifying outliers is by application of Chauvenet’s

criterion (Bevington and Robinson, 2003), which states that, provided

the data follow a normal distribution, we should eliminate a data point

if we expect less than half an event to be further from the mean than the

16.4 Weighting schemes 235

Table 16.3. Comparison of normal and

robust-resistant weight-modiﬁer functions.

Taken from Blessing (1997).

z exp(−z

/2) [1 − min(1, (z

/6)

)]

01 1

1 0.5625 0.945

2 0.135 0.790

3 0.011 0.5625

4 3.3 × 10

−4

0.309

5 3.7 × 10

−6

0.093

6 1.5 × 10

−8

7 2.3 × 10

−11

suspect point. The most extreme point in the 114 data set is at 1684.87,

or 3.81σ from the mean. How many data would we expect beyond this

point? Tables that list values of the integral

√

2π



−z

exp

−

dx (16.19)

are available in most statistical text books. This corresponds to the area

underneath a normal pdf within μ ± zσ, that is the probability that a

measurementwill fall into this range. Tables give the value of the integral

forz = 3.81as0.99985530.In67 measurementsofthis intensity we expect

67 × (1 − 0.99985530) = 0.01 measurements this far from the mean. As

this is 0.5 we should delete this point.

An alternative, more ﬂexible, procedure that can also account for the

long tails in experimentally derived distributions is to down-weight

data by multiplying conventionally derived weights by a modiﬁer func-

tion. A frequently used choice is the robust-resistant or Tukey scheme

(Prince, 1994; Price and Nicolson, 1983; Press et al., 1992):



= w

1 −





, (16.20)

if z

< 6, and w



= 0 otherwise. Table 16.3 (Blessing, 1997) compares the

weights that would be obtainedfor normal and robust-resistantschemes

and it can be seen how the robust-resistant scheme can accommodate the

long tails of experimentally observed distributions (compare the values

in Table 16.3 for a point 4σ from the mean), but also identify serious

outliers.

16.4.3 Assessing weighting schemes

The most widely used test to determine whether weights are on the cor-

rect scale is the χ

test described above. In crystallographic reﬁnements

we tend to calculate the value of S =



red

, the goodness of ﬁt, instead.

236 Random and systematic errors

A value near 1.0 implies that the weights are on the correct scale. In

practice, the value of S can be manipulated to be near unity by dividing

all the w

by χ

red

, and so, unless the σs derived from data process-

ing are being used without modiﬁcation in the weighting scheme, this

parameter has little value.

A more useful procedure, also mentioned above, is to examine how

the values of w

vary when the data are arranged in some systematic

way, and this is referred to as an analysis of variance. In the merging pro-

cedure in SORTAV (Blessing, 1997) this analysis is based on resolution

and intensity to derive more realistic estimates of the standard devia-

tions of the merged intensities. In structure reﬁnement, when S or χ

red

plotted against F

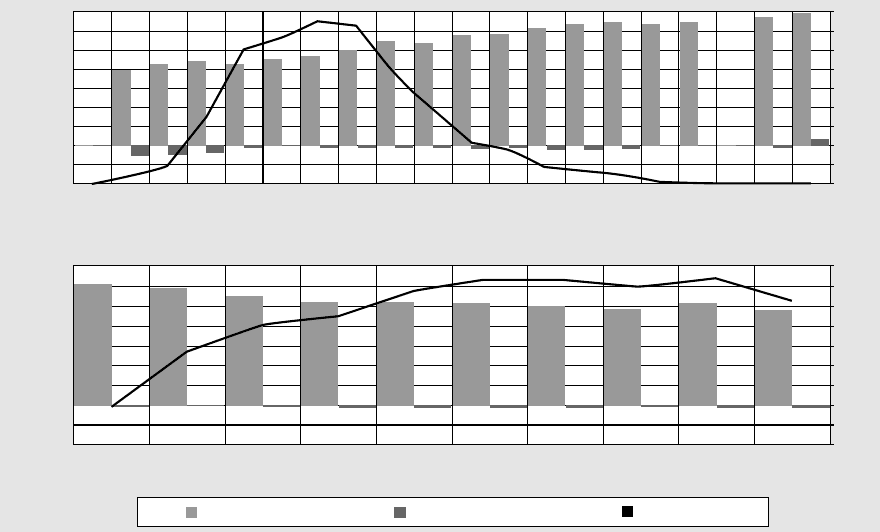
,orsinθ/λ, or index, the line should be ﬂat (Fig. 16.7).

Trends in the values of residuals across different groups (especially

different ranges of resolution and of structure-factor amplitude) reveal

the presence of systematic errors in the model (e.g. neglect of hydrogen

atoms or of extinction effects) or imperfections in the weighting scheme.

Indeed, empirical adjustments to the weighting scheme can be made on

the basis of such an analysis; the weights thus obtained are supposed to

reﬂect not only uncertainties in the data, but also shortcomings of the

structural model.

0.01

0.000

<Fo–Fc>**2 <Fo–Fc>**2

0. 1. 3. 7. 13. 20. 28. 39. 51. 64. 79. 96. 114. 134. 155. 178. 202. 228. 256. 285.

0.040 0.080 0.120

<- Low angle Sin(theta)/lambda High angle ->

<- Weak Fc Range Strong ->

0.160 0.200 0.240 0.280 0.320 0.360

0.1

100

1000

10000

100000

1e+006

1e+007

0.01

Key:

0.1

100

1000

10000

100000

1e+006

1e+007

350

450

350

Number of Reflection Number of Reflection

300

250

200

150

100

400

300

250

200

150

100

<[ |Fo| - |Fc| ]**2>

<w* [ |Fo| - |Fc| ]**2>

Number of Reflections

Fig. 16.7 Analysis of variance based on intensity (top) and resolution (bottom). Notice that the values of w 

(bars) show a ﬂat distri-

bution. Data calculated using CRYSTALS (Betteridge et al., 2003). Bars representing weighted residuals are very close to 1 and not easy

to see.

16.4 Weighting schemes 237

Another method of assessing the validity of a weighting scheme is

through a normal probability plot (Abrahams and Keve, 1971). The ﬁrst

stage of this analysis is to order the j observations in terms of w

.If

the errors in the data follow a normal distribution (and we hope that

this is being reﬂected in our weighting scheme), then the ith data point

should have a w

 value of z, where z is given by the equation

j − 2i + 1

√

2π



−z

exp



−x



dx = erf



√



. (16.21)

The values of z and w

 can be plotted against each other (usually with

the ideal z values on the x-axis), with +z for i > j/2 and −z for i < j/2.

For example, after ordering 192 w

-values, the 37th had a value of

 =−0.95. 192 − 74 + 1/192 = 0.62, and consulting a table of the

integral of a normal distribution (e.g. on p. 38 in Barlow), gives z for

this to be 0.88. The value to be used in the normal probability analysis

is −0.88 since 37 < 192/2, and so the point to be plotted is (−0.88,

−0.95). In practice, of course, these calculations are accomplished using

computer programs: such a facility exists in some reﬁnement programs

(e.g.CRYSTALS) and statistics packages such as MINITAB have facilities

for calculating so-called normal scores.

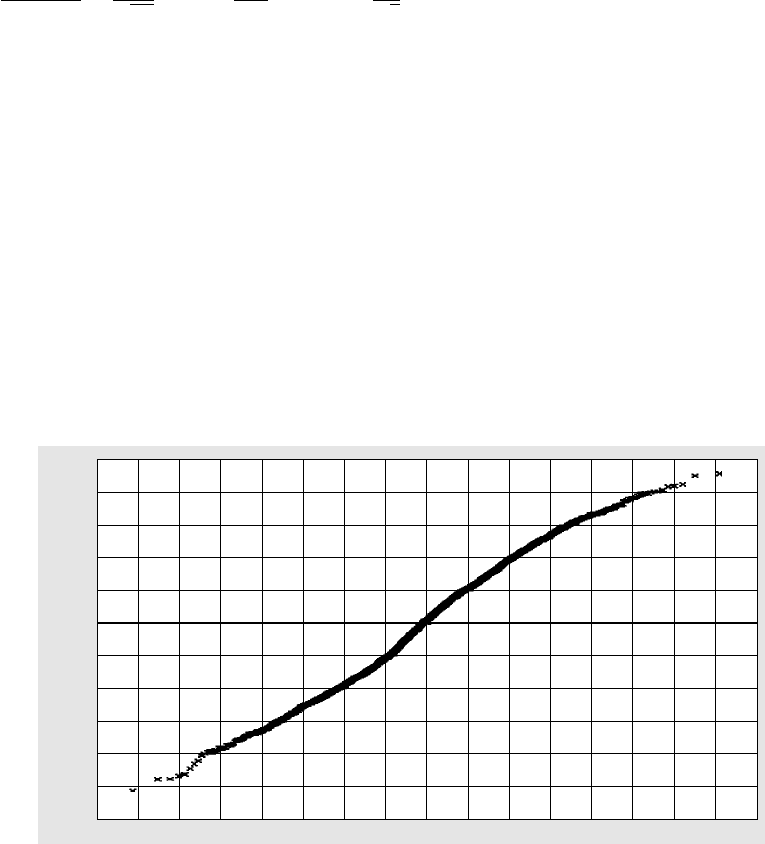
Anormal probabilityplot should be linear, pass throughtheorigin and

have a gradient of 1. An example is given in Fig. 16.8. Non-linear plots

indicate some systematic error of the kind that can not be absorbed by

2.5

1.5

0.5

–0.5

w^.5(Fo-F

)

–1

–1.5

–2

–2.5

–3

–4 –3.5 –3 –2.5 –2 –1.5 –1 –0.5 0 0.5 1 1.5 2 2.5 3 3.5 4

Fig. 16.8 Normal probability plot calculated after a reﬁnement of data collected using a high-pressure cell. The weighting scheme

used here was w

= 1/σ

) with a robust-resistant modiﬁer. The overall gradient is near 1, indicating that the scale of the weights

is reasonable. The slight non-linearity suggests that there are still some systematic errors present in the data, most likely uncorrected

cell-absorption errors. Data calculated using CRYSTALS (Betteridge et al., 2003).

238 Random and systematic errors

the model; a gradient of less than 1.0 would indicate that the weights are

too small (or the σs are too large if these are being used in the weighting

scheme). If the intercept of the plot is not zero, this may indicate a scaling

problem.

Such plots are useful, not only in assessing weighting schemes and

the agreement between observed and calculated set of data, but in any

comparison of two sets of quantities (e.g. two independently measured

datasets for the same structure, or two sets of parameters reﬁned from

them). For the comparison of two independent sets of measured data,

for example, we would use

1,i

− F

2,i

1,i

) + σ

2,i

)

, (16.22)

and then sort the deviations δ

into order of increasing value from the

most negative to the most positive. Probability plots can also be adapted

for testing any probability distribution function.

16.5 Analysis of the agreement between

observed and calculated data

16.5.1 R factors

Before we are able to calculate the desired geometrical information from

the reﬁned atomic parameters, reﬁnement must reach convergence. But

is this convergence the best that can be achieved for our structure? At

several stages during a typical structure determination, reﬁnement con-

verges, but the introduction of more parameters (a change in the model

being reﬁned) allows further reﬁnement to take place, giving conver-

gence again, this time (we hope) to an even better agreement with the

observed data. Such developments of the model are, for example, the

replacement of isotropic by anisotropic atomic displacement parame-

ters, and the inclusion of hydrogen atoms. Other changes that can be

made are the reﬁnement of parameters for effects such as extinction

or absorption, the addition of models of disorder, and changes to the

weighting scheme. Any change in the model will produce a different

set of reﬁned parameters. How do we assess the agreement with the

observed data and choose the ‘best’ model?

Overall ‘residuals’ (single-value measures of the agreement) com-

monly used and quoted are:

R =







wR =









o,i



(16.23)

R is long established as the traditional ‘R factor’, accorded a general

reverence far in excess of its real signiﬁcance. The ‘generalized R factor’,

16.6 Analysis of the agreement between observed and calculated data 239

called wR here in accordance with current Acta Crystallographica usage,

is variously referred to as RG, R



and R

as well.

All of these residuals can be manipulated and massaged in various

ways to produce an apparently better ﬁt to the data. Both R and wR

can be reduced dramatically by omitting some reﬂections, especially

the weak ones and a few that give particularly poor agreement between

| and |F

| (perhaps on grounds such as ‘they are strongly affected

by extinction’). A much better assessment of the ﬁt of observed and

calculated data comes from an analysis of varianceor normal probability

plots as described above.

16.5.2 Signiﬁcance testing

Increasing the number of reﬁned parameters will always (given suitable

weights) reduce the residuals and produce a better ﬁt to the observed

data. It does not follow that any such reduction is signiﬁcant and

meaningful.

The standard test for assessing statistically the improvement in ﬁt

when the model is changed is by analysis of χ

values from the different

models. Ratios of pairs of χ

values follow a so-called F-distribution, but

Hamilton (1971) adapted this for ratios of the wR residuals:

=

wR(1)

wR(2)

(16.24)

for comparison with tabulated values. The tables are constructed for dif-

ferent ‘dimensions’ (the difference in number of parameters for models

1 and 2) and ‘degrees of freedom’ (N − P for model 2) and according to

various ‘levels of signiﬁcance’ α. Thus, if the value of  is greater than a

tabulated value appropriate to the degrees of freedom and dimension of

the test, this means that the probability that this apparent improvement

couldarise by chance fromtwo equally goodmodelsis less than α; model

2 is said to be better than model 1 at the α signiﬁcance level (α is often

expressed as a percentage). So a signiﬁcance level of α = 0.01 (1%), for

example, indicates that there is a 1% risk of accepting the second model

as better when it actually is not.

Interpolation is often necessary between tabulated values, because

the available tables do not cover exactly the dimension and degrees of

freedom required. In practice, it is rare for these tests to indicate that

improvement is not signiﬁcant, and there are some doubts as to their

true statistical validity.

Note that the s.u.s of the reﬁned parameters do not necessarily

decrease when the residuals decrease. Although they do depend on the

minimization function





, they also depend inversely on the excess

of data to parameters, N − P. A very simple assessment of the signiﬁ-

cance of the improvement of a model on introducing extra parameters

is, then, to see whether the parameter s.u. values are reduced.

240 Random and systematic errors

16.6 Estimated standard deviations and

standard uncertainties of structural

parameters

In crystal-structure determinations we do not usually determine a

structure several times in order to obtain mean values of the atomic

parameters and estimates of the variance of these parameters. Instead

we obtain ‘estimated standard deviations’ (e.s.d.s or s.u.s) from a single

experiment. This is possible because our experimentally measured data

(diffraction intensities) greatly outnumber the parameters to be derived:

the problem is said to be over-determined. The value obtained for the

parameter is our best estimate of the true value. The s.u. is a measure of

the precision or statistical reliability of this value; it is our best estimate

of the variation we would expect to ﬁnd for this parameter if we were

to repeat the whole experiment many times. The s.u. we obtain from

reﬁnement is analogous to the standard error on the mean deﬁned in

(16.12).

In structure reﬁnement by least squares, a number of parameters

are determined from a larger number of observed data. The quantity

minimized is



i=1



, (16.25)

where

is usually either |F

−|F

or F

o,i

−F

c,i

and each of the N reﬂec-

tions has a weight w

. The s.u. values of the reﬁned parameters depend

on (i) the minimized function; (ii) the numbers of data and parameters;

(iii) the diagonal elements of the inverse least-squares matrix A

−1

σ(p

) =



−1

)



i=1



N −P



, (16.26)

where p

is the jth of the P parameters (16.26). Note that low s.u. values

(high precision) are achieved with a combination of good agreement

between observed and calculated data (small numerator) and a large

excess of data over parameters (large denominator).

16.6.1 Correlation and covariance

The parameters describing a crystal structure are not independent.

When we derive further results from a combination of several param-

eters (such as calculating a bond length from the six co-ordinates of

two atoms), it is important to recognize this interrelationship in order

to calculate the correct s.u.s for the secondary results.

When variables are not statistically independent, they are said to

be correlated. Just as individual variables have variances, so correlated

16.6 Estimated standard deviations and standard uncertainties of structural parameters 241

variables have covariances. For a discrete distribution of two correlated

variables x and y, the covariance is deﬁned as

cov(x, y) =

N −1



i=1

− x)(y

− y), (16.27)

which should be compared with the variances

(x) =

N −1



i=1

− x)

and σ

(y) =

N −1



i=1

− y)

(16.28)

thus, cov(x, x) = σ

(x) by deﬁnition. For a continuous distribution,

similarly

cov(x, y) =



(x − x)(y − y)P(x, y)dxdy



P(x, y)dxdy,

(16.29)

where c and d are the lower and upper limits of the variable y.

In both cases, the correlation coefﬁcient of x and y is

r(x, y) =

cov(x, y)

σ(x)σ(y)

, (16.30)

and this must lie in the range ±1. A correlation coefﬁcient of exactly

+1or−1 means that x and y are perfectly correlated – each is an exact

linear function of the other, and only one variable is actually required to

describe them both. If x and y are completely independent, their covari-

ance and correlation coefﬁcient are both zero, though the converse is not

necessarilytrue(a covariance of zerodoes not have to mean independent

variables).

Covariances (and hence correlation coefﬁcients) of all pairs of reﬁned

parameters for a crystal structure are obtained together with the

variances from the inverse matrix:

cov(p

, p

) = (A

−1

)



i=1



N −P

. (16.31)

Once we have all the variances and covariances of a set of quantities

(such as the reﬁned atomic parameters), we can calculate the variances

and covariances of any functions of these quantities (such as molecular

geometry parameters).