Blake A.J.(ed.) Crystal Structure Analysis

Подождите немного. Документ загружается.

192 Analysis of extended inorganic structures

20000

40000

60000

80000

100000

120000

140000

30 35 40 45 50 55 60 65 70

2-theta

Intensity

(a)

(c)

(b)

(d)

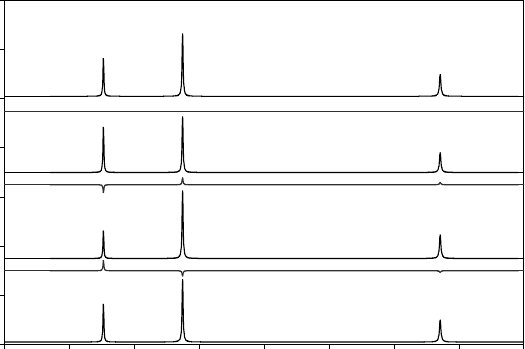
Fig. 14.2 Calculated diffraction patterns for (a) TiO, (b) Ti

0.8

O, (c) TiO

0.8

and (d) Ti

0.8

Thelineunderneatheachcalculatedpatternshowsthediscrepanciesobtained when trying

to ﬁt the structure of stoichiometric TiO to the data, reﬁning only an overall scale factor.

Data for Ti

0.8

are indistinguishable from those for TiO.

What if there are vacancies on both the metal and oxygen sites? As

can be seen in Fig. 14.2, for δ = ε the diffraction pattern of a disordered

1−δ

1−ε

materialisidentical to that of MO. This might seem an ‘exotic’

issue to worry about, but even a material as simple as ‘stoichiometric’

TiO actually contains around

6 vacancies on both the metal and oxy-

gen sites. For complex disorder problems the use of other techniques

(chemical analysis, density measurements, oxidation-state determina-

tion by other techniques, electron microscopy, solid-state NMR, etc.)

can therefore be vital.

14.2.2 Positional disorder

A second type of disorder frequently encountered is positional disorder

where an atom, or a group of atoms, can occupy one of two or more

sites in a structure. In some cases this is a genuine phenomenon and

can be tackled by introducing partial occupancy on several sites, often

coupled with suitable constraints or restraints. In other cases, however,

apparent disorder could arise due to the wrong choice of space group

or twinning. It should not be forgotten that site and occupational order

may be connected. If one had amaterial with a solid solution of La

(r =

1.30 Å) and Bi

(r = 1.31 Å) on the same site one might not be surprised

if the active lone-pair cation Bi

adopted a slightly different position to

. How does one deal with this during reﬁnement? How does one

relate adps for the two cations? Ingenuity and a critical viewpoint are

required!

14.2 Disorder 193

14.2.3 Limits of Bragg diffraction

It should be remembered that Bragg diffraction can only ever tell you

about the average long-range structure of a material and that this can

potentially hide signiﬁcant features of its structure. Consider the two

structures in Fig. 14.3. Both represent a simple material in which 30%

of the available sites are vacant. The two structures can be readily dis-

tinguished visually: in one the vacancies are randomly distributed; in

the second they are clustered – if one site is vacant the adjacent site is

more likely to be vacant. Clearly, real-world examples of such mate-

rials could have drastically different properties. Bragg scattering is,

however, completely blind to these differences and the diffracted inten-

sities of hkl reﬂections of the two materials are identical (Fig. 14.3). The

difference in the structures is revealed only by looking at the diffuse

scattering between Bragg peaks. In a single-crystal experiment this is

seen as streaks between hkl reﬂections; in a powder experiment it is one

contribution (of several) to the background scattering. The examples in

Fig. 14.3 were kindly supplied by Thomas Proffen. There is an excellent

website that explores these ideas further and allows on-line simulations

Intensity (*10

)

12345

[h 2 0]

Intensity (*10

)

123 45

[h 2 0]

12 34 5

h [r.l.u.]

k [r.l.u.]

12 34 5

h [r.l.u.]

k [r.l.u.]

Fig. 14.3 Cross-sections of a 50 × 50 atom structure containing 30% vacancies (drawn as light dots). Bragg scattering (centre plot is of

h, 2, 0 reﬂections) for a randomly disordered and a clustered model is identical. Differences can be seen only in the pattern of diffuse

intensity (right).

194 Analysis of extended inorganic structures

at www.totalscattering.org/teaching (Proffen et al., 2001; see also Neder

and Proffen, 2008; Egami and Billinge, 2003).

Fig. 14.4 The ideal structure of WO

14.3 Phase transitions

Phase transitions are a feature of much of the structural chemistry of

extended materials. WO

is an apparently simple structure made up of

corner-sharing WO

octahedra (Fig. 14.4). As such, one might expect it

to have a simple ∼4 Å cubic unit cell and space group Pm

3m. In reality,

however, its structural chemistry is far more complex. Phase transitions

can occur that involve coupled tiltings of the WO

octahedra, and/or in

which W atoms move from the centres of octahedra in different direc-

tions. WO

is said to show more phase transitions than any other oxide

and it is only recently that controversy over the true structures of some

of the phases appears to have been resolved.

Part of the difﬁculty caused by phase transitions (particularly dis-

placive phase transitions) is that they often lead to only subtle changes

in diffraction patterns, with the relative intensities of reﬂections related

by symmetry in the high-symmetry form showing only slight changes.

Powder diffraction, in which the splitting of, e.g., a cubic 200 reﬂection

into the 200, 020 and 002 reﬂections of an orthorhombic system as the

cell metric changes from a = b = c to a ∼ b ∼ c can sometimes be directly

observed, is often a powerful tool – particularly as it avoids the prob-

lems of twinning in single-crystal samples. Phase transitions will often

lead to the formation of superstructures in which the dimensions of one

or more cell edges are doubled or tripled relative to the high-symmetry

structure. If the atoms that move most in the phase transition make only

a small contribution to diffraction (e.g., the movement of oxygen atoms

in a metal oxide), such effects can again be easily missed.

Finally, phase transitions can also lead to incommensurately modu-

lated structures that present further structural complexity. Consider the

simple structure in Fig. 14.5 that represents a one-dimensional chain of

atoms with a repeat distance a. If a structural change occurs in which

each atom is displaced laterally according to the magnitude of a sine

λ=3a

λ~3a

Fig. 14.5 Schematic representation of the formation of (left) a commensurate superstructure with a = 3a

sub

and (right) an

incommensurate superstructure.

14.4 Structure validation 195

wave with λ = 3a, then this can easily be seen to cause a tripling of the

a-axis. In a diffraction pattern one would expect extra reﬂections to be

observed at points in reciprocal space between the original reﬂections

(withindicesnh/3, k, l comparedtotheoriginal subcell reﬂections).What

if the sine wave describing the structural displacements is not exactly

λ = 3a but λ ∼ 3a? The basic structure of the material produced(Fig. 14.5

right) is clearly very similar to that in Fig. 14.5 left. However, the unit

cell of the material is no longer a simple multiple of the original subcell.

One would again expect to see extra superstructure reﬂections, but they

would no longer appear at simple rational positions between the subcell

reﬂections. It might be that one can approximate the system by choosing

a very large supercell. For example, in Fig. 14.5 one could approximate

the superstructure using a

sup

= 10a

sub

. However, this is clearly a rather

inelegant approach as one now has a large unit cell requiring a large

number of atoms in the asymmetric unit. There is a more natural lan-

guage to describe such systems – that of ‘incommensurately modulated

structures’ – which can be used to describe either positional or com-

positional ﬂuctuations in materials. This language views the periodic

superstructure merelyas aspecialcase of the moregeneral phenomenon.

More detailed information can be found in a number of places, but is

beyond the scope of this text.

14.4 Structure validation

Assuming that one has successfully solved the structure of an inorganic

material, how can one be sure it is correct? For small-molecule work an

experienced crystallographer will know that a C–C bond length should

be about 1.54 Å, and C=C 1.34 Å; for more exotic distances one can eas-

ily consult the Cambridge Structural Database (Allen, 2002). Distances

signiﬁcantly different from those expected would immediately cause

concern about the structural model. For inorganic materials such com-

parisons are harder. Co-ordination environments are far less regular,

the range of possible environments is larger, different oxidation states

of elements have different geometric preferences, and there is no direct

equivalent of the CSD to consult.

†

Whilst simple structural considera-

†

There are inorganic databases available

such as the ICSD, PDF-4 and Pauling ﬁle,

but they are not as readily interrogated as

the CSD. Inorganic structures can be read

into CSD software to provide searchable

databases but one should always be aware

of bias in the data. How does one take

account of the fact that, e.g., TiO

appears

113 times in the database when trying to

decide an average Ti–O distance for a range

of materials?

tions using ionic radii (the sets derived from those initially published

by Shannon and Prewitt in 1969 are the the most widely used; see, for

example, Shannon, 1976) are possible, they are often not desperately

informative.

One relatively straightforward approach is to make use of the bond-

valence concept popularized by Brown and Altermatt (1985), which

builds on ideas originally applied to metals and intermetallics by Paul-

ing in 1947. The basis of the approach is that each bond from atom i to

atom j is assigned a valence v

such that the sum of valences for bonds

from a given atom equals its total valence, V (=v

). The most widely

used expression for the dependence of bond valence on bond length is:

= exp[(R

− d

)/b]. (14.1)

196 Analysis of extended inorganic structures

Table 14.1. Bond distances and bond valence sums for BiMg

(see case history 1).

values taken from Brese and O’Keeffe (1991) of Bi 2.094, Mg 1.693 and V 1.803

were used.

O1 O1 O1 O1 O2 O3 O3 O4 Sum

Bi1 d/Å 2.199 2.199 2.236 2.236

0.75 0.75 0.68 0.68 2.87

Mg1 d/Å 2.066 2.066 1.980 2.038 2.038

0.36 0.36 0.46 0.39 0.39 1.98

Mg2 d/Å 2.066 2.066 2.042 2.042 1.995

0.36 0.36 0.39 0.39 0.44 1.95

V1 d/Å 1.688 1.733 1.733 1.684

1.36 1.21 1.21 1.38 5.16

Sum (2 × Bi1) 2.16 1.82 1.99 1.82

In this expression d

is the bond length, R

the so-called ‘bond-valence

parameter’ and b a constant usually taken to be 0.37 Å. Whilst the-

oretical justiﬁcations of this method have been published, it is usual

to treat the expression as an empirical but effective tool. Brese and

O’Keeffe (1991) have taken this approach and published bond-valence

parameters R

for most common cation–anion combinations using over

1000 carefully chosen crystal structures. These values can be found

on a number of websites including http://www.ccp14.ac.uk/ccp/web-

mirrors/i_d_brown/.

Bond-valence parameters can be used in a number of ways. The most

obvious is to check the validity of a structural model. If a crystal struc-

ture is correct, then one would expect the bond-valence sum for each

element to be close to its formal valency. Values for a typical inorganic

structure (BiMg

of case history 1) are shown in Table 14.1. Typ-

ically, one would expect valence sums to be within a few per cent of

formal valencies. Values outside this range could suggest an incorrect

model, that one has used valence parameters for the wrong oxidation

state of the element, that the material is highly strained, or that part of

the structure is missing. In this latter context bond-valence sums are par-

ticularly useful for identifying missing H atoms in inorganic structures.

Bond-valence parameters can also be used (via (14.1)) for calculating

expected radii for a given element/anion conﬁguration, or as a criterion

for determining co-ordination numbers (for example, how important is

an oxygen anion at 3.1 Å to the co-ordination environment of a Bi

cation? Answer: it contributes <2% of the valence sum, so not very!).

14.5 Case history 1 – BiMg

Bismuth magnesium vanadate is a material whose structure was ﬁrst

reported in orthorhombic space group Cmcm by Huang and Sleight

(1992). Materials of this type have been investigated for catalytic and

14.5 Case history 1 – BiMg

197

non-linear optical (NLO) properties. With a material of this formula

one might anticipate problems due to pseudo-symmetry (because of

the heavy Bi atom) and signiﬁcant absorption.

To illustrate both these potential pitfalls data have recently been col-

lected on this material using a Bruker SMART 6000 diffractometer using

Mo-Kα radiation. Afull sphere of data was collected with a frame width

of 0.3

◦

and a counting time of 20 s per frame. Using a default set of

thresholding parameters the same cell and space group were found as in

the published structure (though we actually chose a non-standard space

groupsetting Bbmm rather than Cmcm for analysis). The structure would

solve and reﬁne without any difﬁculties. Final agreements of R = 2.10%,

wR = 5.64% were obtained for 552 reﬂections after anisotropic reﬁne-

ment and application of an optimal weighting scheme in the Oxford

CRYSTALS suite of software. Bond distances and angles were all close

to expected values and the co-ordinates were essentially as published.

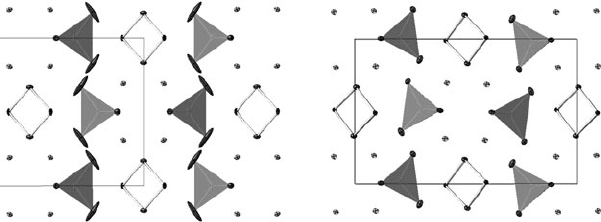
However, it can be seen from Fig. 14.6 that, whilst the adps on most

atoms are what one might expect for a material of this type, one oxygen

atom has an adp that is physically unreasonable and might suggest that

this oxygen site should be split. In fact, careful examination of the raw

frames shows that additional weak reﬂections are present that violate

the cell centring and show that the true space group of this material

is Pnma. Reﬁnement in this lower-symmetry space group proceeded

smoothly, giving ﬁnal R-factors for the 1054 observed reﬂections of

R = 2.13%,wR = 5.27%, with all atoms now showing physically sensi-

ble adps. It can be seen from Fig. 14.6 that the structure is only subtly

different from the Bbmm model. Note that in this case the correct struc-

ture has an R factor that is slightly higher than the incorrect structure

due to the larger number of reﬂections.

In fact, since the original publication this material has been shown

to undergo a displacive phase transition on warming above ∼300 K

from the primitive to the centred structure (Radosavljevic and Sleight,

2000). In the high-temperature structure the oxygen atoms of the VO

Fig. 14.6 Reﬁnements of BiMg

in Bbmm (left) and Pnma (right); both structures are

viewed down the b-axis with a running to the right. The structure contains VO

tetrahedra

(shaded), Bi

chains and 5-coordinate Mg (here shown without bonds for clarity). Adps

have been drawn at the 50% probability level.

198 Analysis of extended inorganic structures

tetrahedra again show extended adps, which this time are indicative of

dynamic disorder (Fig. 14.7).

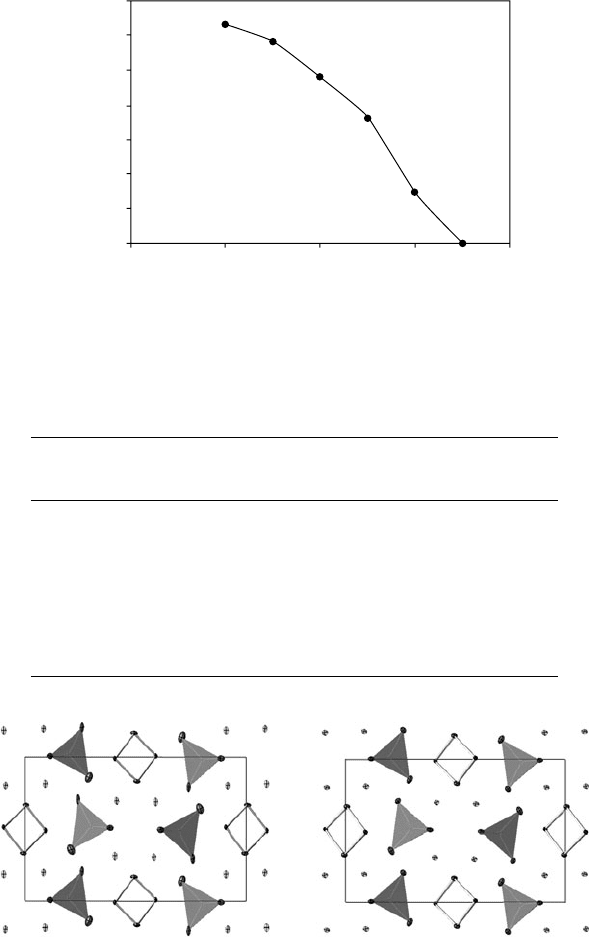
The importance of an adequate absorption correction when working

with materials of this type can be seen from Table 14.2 and Fig. 14.8.

0 100

0.14

0.12

0.10

0.08

0.06

0.04

0.02

0.00

P/A Intensity ratio

200 300 400

Temperature (K)

Fig. 14.7 Relative summed intensities of reﬂections allowed only in Pnma (‘P’ reﬂections)

and those allowed in both space groups (‘A’ reﬂections) as a function of temperature.

Table 14.2. R factors for processing and reﬁnement of BiMg

data.

* failed to converge fully. ** one non-positive-deﬁnite adp.

Untreated

Face

indexed SADABS

FI +

SADABS

int

(%) 25.8 12.8 5.2 2.9

No. reﬂections 8983 8983 7680 8955

R/wR (%), isotropic 7.20/17.53 3.80/10.14 5.44/11.85 2.43/6.36

reﬁnement

R/wR (%), anisotropic 6.70/16.16 3.19/8.47 3.82/8.77* 2.21/6.03

reﬁnement

R/wR(%), aniso ref + 6.75/10.85 3.14/7.05 4.05/7.79** 2.13/5.27

optimal weights

Fig. 14.8 Reﬁnements of BiMg

usingraw(left)andabsorption-corrected data(right);

both structures are viewed down the b-axis with a running to the right. Key as for Fig. 14.6.

14.6 Case history2–Mo

199

The crystal used for these experiments was an elongated prism of

dimensions 0.02 × 0.03 × 0.27 mm. Without any absorption correction

a merging R factor of 25.8% was obtained. On full anisotropic reﬁne-

ment ﬁnal agreement factors of R = 6.75, wR = 10.85% were achieved.

The best model could be obtained by application of a combined face-

indexedandSADABS-typeabsorptioncorrection,resultingin a merging

R factor of 2.9% and ﬁnal agreement factors of 2.13/5.27%. Signiﬁcant

improvements in the shape of adps were observed (Fig. 14.6).

14.6 Case history2–Mo

From its formula Mo

would appear to be a relatively simple

inorganic material and one might therefore expect it to have a simple

structure. In fact, the structure of the material was reported by Costentin

et al. (1992) in space group P2

/c with unit cell parameters a = 8.3065,

b = 6.5154, c = 10.7102 Å, β = 106.695

◦

, V = 555.20Å

. The cell thus

contains a total of 2 formula units and can be described using 11 atoms in

the asymmetric unit. The structure contains MoO

octahedra that share

5 of their 6 corners with PO

tetrahedra. The PO

tetrahedra themselves

share corners to give P

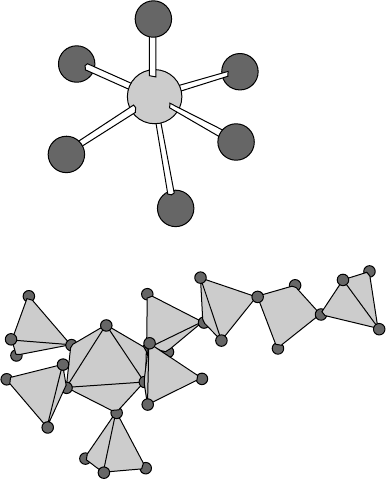
groups (Fig. 14.9). However, despite the

structure being chemically plausible and having an R factor of 3.6%,

there were certain features that were puzzling, including (see Fig. 14.10)

rather large adps on certain atoms.

2.03

2.04

1.65

2.01

2.09

2.15

Fig. 14.9 Local MoO

and P

environments in the structure of Mo

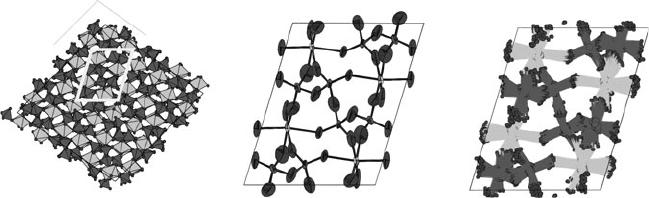
200 Analysis of extended inorganic structures

Fig. 14.10 Left: a polyhedral view of the true superstructure of Mo

; the incorrect small unit cell is also shown. Middle: adps

(drawn at the 70% probability level) derived from 120 K data using the incorrect subcell model. Right: true atomic positions mapped

back onto the incorrect subcell. Notice the similarity between the incorrect adps and the true static displacements of atoms.

When we re-collected data on this material using a Bruker SMART

6000 it became clear that the true unit cell of this material was consid-

erably more complex than had been initially realized. The actual cell

volume was some 21 times larger than that originally reported, the true

room-temperature cell parameters being a = 24.133(2), b = 19.579(2),

c = 25.109(2) Å, β = 99.962(3)

◦

, V = 11685.13 Å

. The unit cell must

then contain some 42 formula units. Automated data processing using

the Bruker XPREP software suggested that the space group was P2

/n.

However,carefulmanualinspection of thereﬂectionlistingrevealedthat

reﬂections forbidden by the 2

axis were in fact present, albeit weak [the

strongest 0k0 reﬂection observed with k = 2n was 070 with I = 1.54(3);

this ranked 13 352nd of the observed reﬂections ordered by intensity;

by comparison the strongest reﬂection observed had I = 9300(120)],

meaning that the true space group was Pn. This in turn implies that the

asymmetric unit of the material must contain 441 independent atoms –

some 430 more than originally thought!

Solving a structure of this complexity that displays severe pseudo-

symmetry is clearly challenging. We took the approach of ﬁrst solving

the substructure using the unit cell originally published. Using 120 K

data we could reﬁne the substructure to R = 9.5%, though again adps

on certain atoms were rather large. By comparing the indices hkl of

certain reﬂections based on the (wrong) small unit cell with those of

the correct larger cell we could obtain a transformation matrix to relate

the two structures (see Exercise 3 at the end of this chapter). We could

then transform the subcell co-ordinates to give a starting model for the

high-temperature structure.

Despite now having a chemically plausible starting model, least-

squares reﬁnement is not straightforward. As described in Chapter 13,

if one tries to directly reﬁne a high-symmetry structure in a lower-

symmetry space group the least-squares will invariably diverge. How

then does one move forward? In this case we know a great deal of useful

information about the structure: we know that it contains MoO

octahe-

dra that share corners with PO

tetrahedra; we know from the literature

that MoO

octahedra typically contain 4 Mo–O bonds around 2.05 Å,

14.6 Case history2–Mo

201

1 short M=O around 1.65 Å and 1 longer M–O around 2.20 Å; we know

that P–O bonds of PO

tetrahedra are typically around 1.5 Å; and we

know that P–O bonds in P–O–P linkages are typically slightly longer,

around 1.60 Å. Given this information it is possible to generate a set

of distance restraints to describe the structure and to reﬁne the struc-

tural model, not against a set of diffraction data but directly against the

restraints. The quantity minimized is then the sum of the squared dif-

ferences between prescribed distances and the distances in the model.

Atoms are moved until these differences are minimized. This is called

distance least squares or DLS reﬁnement and has been used to great

effect for many inorganic systems and particularly zeolite frameworks

(see publications by Baerlocher and co-workers). By performing DLS

reﬁnement it is possible to produce plausible structural models, which

can be tested against the data.

In this example it proved relatively straightforward to solve the struc-

ture by simultaneously reﬁning against both the data and the DLS

restraints (252 in total to describe Mo–O distances; 336 to describe P–O

distances; 630/504, respectively, for MoO

/PO

bond angles; Mo–O

restraints were set up in such a way that each octahedron could have a

range of distances to allow for the expected mixture of short and long

bonds). We used a simulated annealing approach in which we started

reﬁnement from the subcell co-ordinates and then reﬁned the structure

against data and restraints simultaneously to convergence. At conver-

gence, co-ordinates were automatically reset to their initial values ± a

small random displacement and the reﬁnement repeated. This process

was performed on a relatively small 2θ range of data for speed, but

rapidly resulted in a solution with a low R factor. This solution was

then reﬁned against the whole dataset without any restraints to give

R = 3.49% and wR = 5.99% for 43783 reﬂections with I > 3σ(I).It

is perhaps worth noting that new charge ﬂipping methods can solve

pseudo-symmetry problems such as this far more easily.

The true structure of Mo

is necessarily complicated! Fig. 14.10

shows the structure in polyhedral representation. The ﬁgure also shows

a comparison of the incorrect literature model with the true structure

‘folded back’ into the small unit cell (this can be done by applying the

reverse of the transformation matrix used to generate the initial super-

structure model). Here, each of the atomic positions in the true supercell

becomes one of several closely separated positions in the subcell. It is

instructive to note that the shape of the adps obtained using the incorrect

small cell are closely related to the true static displacements of atoms in

the larger cell.

How can one judge the quality of a structural model for an inor-

ganic crystal structure such as this? Normally one would compare bond

distances and angles with expected values or calculate bond valence

sums for the various atoms in the structure. With a structure this com-

plex (it contains 42 different MoO

octahedra and 84 PO

tetrahedra),

the structure can be checked for internal self-consistency – it acts as

its own database. Isotropic displacement parameters for all atoms lay