Blake A.J.(ed.) Crystal Structure Analysis

Подождите немного. Документ загружается.

162 Least-squares ﬁtting of parameters

smaller system of equations than we had before. The original variables

x are then obtained from (12.19).

To illustrate this using the angles of a triangle, we can express γ in

terms of α and β by the constraint γ = 180 − α − β. We will call the

reduced set of unknowns u and v such that

⎛

⎝

⎞

⎠

⎛

⎝

−1 −1

⎞

⎠





⎛

⎝

180

⎞

⎠

, (12.21)

and substituting for α, β, γ in the observational equations gives

⎛

⎝

−1 −1

⎞

⎠





⎛

⎝

−125

⎞

⎠

. (12.22)

The normal equations of least squares are









198

171



, (12.23)

which give u = 75, v = 48,

that α = 75, β = 48 and γ = 57. No

weights were used in this illustration, so all angles are shifted by the

same amount and their sum is exactly 180

◦

12.3 Non-linear least squares

At this point we discover that someone else in the surveyor’s ofﬁce has

also measured the ﬁeld, except he obtained the lengths of the three sides.

These are a = 21 m, b = 16 m, c = 19 m. We can now do even better than

before, because additional information is at hand. The sides are related

to the angles using the sine rule. That is:

sin α

sin β

sin γ

, (12.24)

which gives additional equations that can be added to our set. The difﬁ-

culty is that the new equations are non-linear and, in general, there is no

direct way of solving them to obtain values of the parameters. However,

we need to be able to deal with these as well, since the equations for the

reﬁnement of crystal structures are also non-linear.

Let us use the new equations ﬁrst of all as restraints. That is, they are

simply added to the observational equations with appropriate weights.

12.3 Non-linear least squares 163

Our unweighted observational equations could now be:

2α = 146

◦

β = 46

◦

γ = 55

◦

a = 21 m

b = 16 m

c = 19 m

a sin β − b sin α = 0m

b sin γ − c sin β = 0m

α + β +γ = 180

◦

(12.25)

i.e. nine equations in six unknowns. However, four of the equations

give the value of an angle, while the remaining ﬁve give a length.

How can you compare length measurements with angle measurements?

Does it matter whether you express the angles in terms of degrees or

radians? This can all be taken care of in the weights assigned to the

equations. A proper weighting scheme will make the expected variance

of each weighted equation numerically the same and make sure that

the expected errors in the parameters all have the same effect upon the

equations. However, it is unnecessary to go into such details here. The

same problem arises in the reﬁnement of crystal structures where, for

example, atomic displacement parameters are determined along with

atomic positional parameters. Surprisingly, not every crystallographic

least-squares program does this properly.

Using the current values of the sides and angles of the triangle will

not satisfy the last three equations in (12.25). Our aim is to minimize

the sum of the squares of the residuals of all the equations by adjusting

the values of a, b, c, α, β, γ , thus giving the least-squares solution. Now

let us see how this least-squares solution may be obtained. Let the ith

non-linear equation be f

, x

, ..., x

) = 0 whose jth parameter is x

The derivative of f

with respect to x

is ∂f

/∂x

. We can set up a matrix,

A, of such derivatives so the element a

is ∂f

/∂x

. There will be as many

rows in the matrix as observational equations and as many columns as

parameters. We can also calculate the residual, ε

, of each equation using

the current parameter values. The shifts x to the parameters can then

be calculated from the equations Ax =−ε, where ε is the vector of

residuals. When there are more equations than unknowns, least-squares

values are obtained by solving

A)x =−A

ε. (12.26)

The shifts to the parameters are then applied to give new values

new

= x

old

+ x, (12.27)

164 Least-squares ﬁtting of parameters

which should satisfy the observational equations better than the old

values.

However, this recipe is strictly valid only for inﬁnitesimally small

shifts and is an approximation for parameter shifts of realistic size. This

means the new parameter values are still only approximate and further

shifts need to be calculated. A process of iteration is therefore set up, in

which the latest parameter values are used to obtain new shifts and the

operation is repeated until the calculated shifts are negligible.

Applying the recipe to the triangle example gives the matrix of

derivatives

⎛

⎜

⎝

100000

010000

001000

000100

000010

000001

−b cos α a cos β 0 sin β −sin α 0

0 −c cos β b cos γ 0 sin γ −sin β

111000

⎞

⎟

⎠

, (12.28)

which is used to set up the equations for the parameter shifts.

Note that, in order to apply this method of ﬁtting the parameters to

the experimental measurements, we need to begin with approximate

values that are then adjusted to improve the ﬁt with the experimental

data. There is generally no way of determining these values directly

from the non-linear equations.

12.4 Ill-conditioning

You are probably very familiar with the general rule that if anything can

go wrong, it will. There are many traps for the unwary in least-squares

reﬁnement, but one that everyone must know about is ill-conditioning.

Consider the innocent-looking pair of equations:

23.3x + 37.7y = 14.4

8.9x + 14.4y = 5.5.

(12.29)

The exact solution is easily conﬁrmed to be x =−1, y = 1. However,

in the equations we normally deal with, the coefﬁcients are subject to

error – either experimental errors or errors in the model. Let us simulate

a very small error in (12.29) by changing the right-hand side of the ﬁrst

equation from 14.4 to 14.39. Solving the equations this time yields the

resultx = 13.4, y =−7.9. The equations are,in fact, ill-conditioned and a

very small change in the right-hand side has made the solution unrecog-

nisably different. The computer will also introduce its own errors into

the calculation, because it works to a limited precision. How can we

12.5 Computing time 165

trust the solution of a system of equations ever again? We clearly need

to recognize ill-conditioning when we see it.

Acommon way of recognizing an ill-conditioned system of equations

is to calculate the determinant of the left-hand-side matrix. In this case

it is −0.01. An ill-conditioned matrix always has a determinant whose

value is small compared with the general size of its elements. Another,

related, symptom is that the inverse matrix has very large elements. In

this case, the inverse is



−1440 3770

890 −2330



. (12.30)

Since the inverse matrix features in the formula (12.9) for calculat-

ing the variance–covariance matrix, an ill-conditioned normal matrix of

least squares automatically leads to very large variances for the derived

parameters.

In an extreme case, the determinant of the left-hand-side matrix may

be zero. The matrix is then said to be singular and the equations no

longer have a unique solution. They may have an inﬁnite number of

solutions or no solution at all. Physically, this means the equations do

not contain the information required to evaluate the parameters. If the

information is not there, there is no way of getting it from the equations.

To make progress, it is necessary either to remove the parameters that

are not deﬁned by the observations, or to add new equations to the

system so that all the parameters are deﬁned. There are a number of

ways of producing a singular matrix in crystallographic least-squares

reﬁnement. Easy ways are to reﬁne parameters that should be ﬁxed by

symmetry, or to reﬁne all atomic positional parameters in a polar space

group: the symmetry does not deﬁne the origin along the polar axis, so

the atomic positions in this direction can have only relative values.

12.5 Computing time

Most computing time in X-ray crystallography is spent on the least-

squares reﬁnement of the crystal structure. An appreciation of where

this time goes may help crystallographers usetheir computing resources

more efﬁciently.

The observational equations are mainly the structure-factor

equations, e.g.





j=1

exp[2πi(hx

+ ky

+ lz

)]



(hkl)

, (12.31)

which contain the atomic positional parameters for N atoms, and will

usually also contain the atomic displacement parameters in addition to

occupancy factors, scale factors etc. There will be as many equations as

166 Least-squares ﬁtting of parameters

observed structure factors; let this be n, with p parameters describing the

structure. If the calculation proceeds by setting up the normal equations

of least squares, this will be the most time-consuming part of the whole

process. The matrix multiplication alone (to form A

A) will require

about np

/2 multiplication operations. With p equal to a few hundred

and n equal to a few thousand, np

/2 will typically be a few tens of

millions (∼10

). Efﬁcient computer algorithms can reduce this to a few

times np operations, i.e. of the order of 10

, but it is still large.

The amount of work required to solve the normal equations is about

/3 multiplications, while it takes about p

multiplications to invert

the matrix. Note that it is unnecessary to invert the matrix to solve the

equations and so the matrix inverse should only be calculated when it is

needed for the estimation of variances. Again, computer times may be

reduced by using efﬁcient algorithms, but matrix inversion will always

take a lot less time than that required to set up the normal equations.

Exercises 167

Exercises

1. Show how (12.13) was derived and verify the least-

squares solution.

2. Determine the slope and intercept of the line of linear

regression through the points (1, 2), (3, 3), (5, 7), giving

equal weight to each point.

3. Using data from Exercise 12.2, invert the normal matrix

and, from this, calculate the correlation coefﬁcient μ

between the slope m and intercept c.

4. In the triangle problem, let the expected errors in α, β, γ

be in the ratio 1:2:1.

a) Set up the weighted observational equations for

α, β, γ and include the restraint α + β + γ = 180

◦

at half the weight of the equation α = 73

◦

b) Set up the normal equations of least squares from

the observational and restraint equations.

c) Conﬁrm that the solution of the normal equations

is α = 73.6

◦

, β = 48.4

◦

, γ = 55.6

◦

5. In the triangle problem, let the observational equations

be α = 73

◦

, β = 46

◦

, γ = 55

◦

, a = 21 m, b = 16 m,

c = 19 m, and use the two restraint equations a

+ c

+ 2bc cos α and α + β + γ = 180

◦

. Set up the

matrix of derivatives needed to calculate shifts to the

parameters.

This page intentionally left blank

Reﬁnement of crystal

structures

David Watkin

This chapter is intended to supplement the introduction to the theory

of least squares given in Chapter 12, and provide crystallographic illus-

trations. Fourier methods (Chapter 8) provide a crucial reﬁnement tool,

especially if trial stuctures remain intransigent.

If direct methods are a black box, then reﬁnement is a black art. There

is no recipe book to deal with all situations. Difﬁcult reﬁnements, that

is, ones where the R-factor does not fall as expected, or the results look

anomalous, can be dealt with only by inventing strategies and trying

them. An understanding of the background mathematics and physics,

together with a knowledge of the literature, may enable you to use the

tools provided in your software to overcome the problem.

There is a massive literature, but some selected references are

given here.

Reﬁnement on weak or problematic small molecule data using SHELXL97

(Blake, 2004).

Crystal Structure Analysis: Principles and Practice (Clegg et al., 2001).

Fundamentals of Crystallography (Giacovazzo et al., 2002).

Crystal Structure Reﬁnement: A Crystallographer’s Guide to SHELXL

(Müller et al., 2006).

The Control of Difﬁcult Reﬁnements (Watkin, 1994).

Current Methods and Optimisation Algorithms for the Reﬁnement of X-ray

Crystal Structures (van der Maelen, 1999).

Introduction to Macromolecular Reﬁnement (Tronrud, 2004).

13.1 Equations

Crystal-structure analysis is built on four equations. In order to under-

stand what is happening during reﬁnement, and to enable you to

invent ways of solving problems, it is important to understand these

basics.

169

170 Reﬁnement of crystal structures

13.1.1 Bragg’s law

4 sin

θ/λ

= h

∗2

...+ 2klb

∗

cos α

∗

. (13.1)

Bragg’s law in three dimensions. This tells us that the positions of the

diffraction data in reciprocal space depend only upon the dimensions

and symmetry of the unit cell. If the sample contains domains sufﬁ-

ciently large to cause diffraction, but randomly orientated with respect

to each other, the sample is a polycrystalline powder, and the diffrac-

tion pattern will consist of randomly overlaid reciprocal lattices giving

diffraction ‘rings’. If the domains have simple geometric relationships

between then, the sample is a twin or polytwin, and will give interpen-

etrating but related diffraction patterns for each component. There is

generally systematic overlapping of the lattice points. If adjacent unit

cells differ slightly, but the difference is periodic, the sample is modu-

lated. Correct interpretation of the reciprocal lattice is a pre-requisite for

all analyses.

13.1.2 Structure factors from the continuous

electron density

hkl



xyz

2πi(hx+ky+lz)

∂x . ∂y.∂z. (13.2)

The intensity and phase of each ‘reﬂection’ in a diffraction pattern

depend upon the interaction of the incident wavefront with the con-

tinuous periodic electron density throughout a mosaic block. A mosaic

block is a fragment of crystal in which the alignment of the constituent

unit cells is sufﬁciently accurate to enable interference to occur. Because

diffraction is an interference phenomenon, the resulting diffracted

beams have both an amplitude and a phase. Beams diffracted from adja-

centmosaic blocks (or twin domains)haveno rational phase relationship

between them, so that the resulting intensity is just the sum of the con-

stituent intensities. In general, the intensities can be easily measured

but not the phases; their measurement requires interferometry exper-

iments. Every point in the continuous electron density contributes to

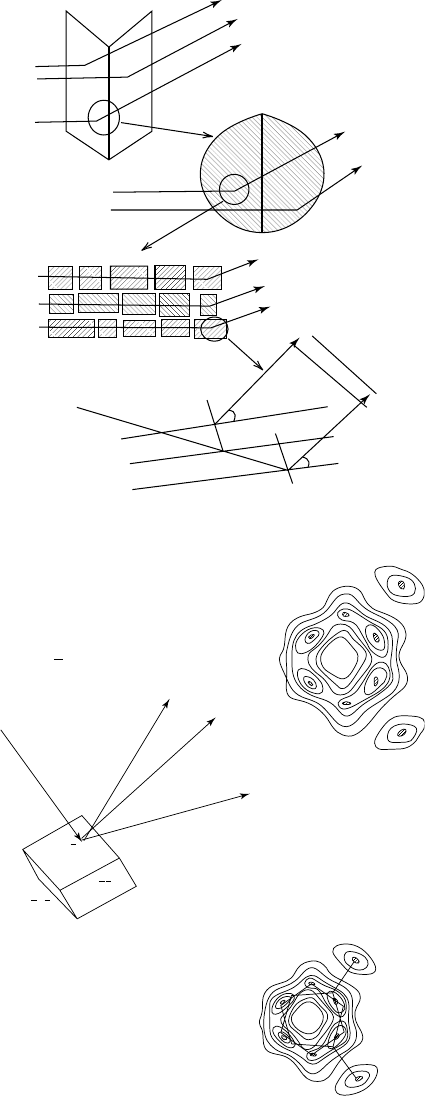
each diffracted beam (Fig. 13.1).

13.1.3 Electron density from the structure amplitude

and phase

xyz



|F|

hkl

−2πi(hx+ky+lz−α

hkl

)

. (13.3)

If the intensity and phase of all the diffracted beams could be measured,

then the electron density at any point in the unit cell could be computed

(Fig. 13.2). Note that every reﬂection contributes to each point in the

unit cell.

13.1 Equations 171

twin

= I

+ I

= I

+ I

F = A +

Fig. 13.1 Diffraction from crystal domains.

10 10

11 30

10 26

4101035

11 39

14 16 16 11

32 26 11

67 47 26 44

65 65 2 10 44 24 10

10 10 11 11

26 26 24

24 24 26 12

18 16 10

25 30 37 37 37 45 40 46 24 22 10

26 25 25 24 30 39 39 60 91 90 40 24 10

31 31 54 54 9 2 2 40 49 40 45 4545

14 45 35 4 2 20 33 32 42 39

xyz



hkl

–2p

(hx + ky + lz – a

hkl

)

1011

hkl

 f

·e

2pi(hxj + kyj + lzj)

hkl



xyz

2pi(hx + ky + lz)

−x.−y.−z

40 20 3 9 34 54 57 21

61 52 52 6 2 20 31 37 12 39

71 20 56 24 4 3 13 8 29 10 14 1512

27 27 27 64 10 19 19 61 61 60 60 26 10

55 65 38 57 50 50 55 51 26 28 27 10

10 34 35 36 37 37 14 27 10

35 32 26 26 17

26 1132

16 15 14

1816 10

15 1228 25

2626 27

11 11

1101

0111

Fig. 13.2 The calculation of electron density from (13.3).