Благовещенский С.Н., Холодилин А.Н. Справочник по статике и динамике корабля. Статика корабля. Том 1
Подождите немного. Документ загружается.


торой сомнительна. При операциях с большими числами такой способ записи, кроме
того, сокращает общее количество выписываемых
цифр.
Пусть, например, в приближенном числе 12 730 000 цифра.3 является сомнитель-
ной;
следовательно, абсолютная погрешность этого числа равна е = 10 000. В соот-
ветствии с указанным правилом его
следует
записать в виде
1,273-10'.
Точно так же, чтобы показать, что число 57 приближенное и ошибка начинается
с пятого знака, надо его писать-так:
57,000
или
5,7000-10»
Если же его написать 5,7 • 10
1
, то это
будет
показывать, что цифра 7 сомнительная.
Наконец,
если число 57 абсолютно точное, например 57 человек, то его
следует
писать 57, не ставя запятой .и не прибавляя нулей.
При
совершении арифметических действий с приближенными числами
следует
руководствоваться следующими указаниями.
При
сложении в том случае, когда слагаемые приблизительно одинаковой вели-
чины
(отношение наибольшего к наименьшему менее 10), надо все их писать с одним
и
тем же количеством знаков после запятой; столько же знаков нужно удерживать
и
в сумме.
Если же приходится складывать числа, хотя и известные с одинаковой степенью
точности, но сильно разнящиеся по величине,
тогда
без ущерба для точности оконча-
тельного
результата
следует
упрощать действия.
Пусть, например, надо сложить имеющие приблизительно одинаковую относи-
тельную погрешность пятизначные числа
52,374;
2,8235;
0,014253;
0,52181.
Сложение
следует
производить так:
52,374
2,824
0,522
0,014
.55,734
т. е., написав наибольшее слагаемое, удерживать в остальных лишь столько цифр
после-запятой, сколько их у наибольшего числа.
При
сложении большого количества слагаемых
следует
учитывать возможность
взаимной
компенсации погрешностей и вместо наибольшей возможной погрешности яб
вводить вероятную погрешность б У^п, где б — абсолютная погрешность, ал — число
слагаемых.
При
умножении ряда сомножителей в произведении
следует
удерживать столько .
цифр,
сколько их в наименее точном из сомножителей. Это же правило распростра-
няется
и на деление, т. е. в частном нужно удерживать столько знаков, сколько их
в
делимом или в делителе, смотря по
тому,
что является менее точным.
При
возведении в степень относительная погрешность
результата
будет
равна
погрешности числа, умноженного на показатель степени. Так, относительная по-
грешность куба числа равна утроенной относительной погрешности этого числа.
Правило
это распространяется и на дробные показатели.
Во многих вычислениях приходится составлять для заданной кривой суммы
.квадратов и кубов ординат, которые снимаются с чертежа. Если ордината известна
с точностью до четвертого знака,'т. е. три значащих цифры верны, а четвертая не-
верна или сомнительна, то и в квадрате, и в
кубе
ее
будут
только первые две верные
цифры,
третья уже может быть сомнительной, а все дальнейшие
будут
неверны.
Поэтому, выписывая из обычных таблиц значения квадратов и кубов ординат,
необходимо эти значения соответствующим образом округлять, увеличивая на еди-
ницу
оставляемую сомнительную цифру, если отбрасывается пять или более единиц
следующего
разряда. - •
При
вычитании
следует
избегать^вычисления малой разности больших величин,
так
как относительная погрешность такого вычисления весьма велика. Поэтому при
вычислениях надо стремиться так преобразовывать формулы, чтобы малые разности
двух
величин можно было вычислять непосредственно, не вычисляя самих величин.
При
пользовании логарифмами
следует
§рать их с таким числом знаков, сколько
всех
их в подлежащих вычислению числах, поэтому в теории корабля вполне доста-
точно четырехзначных таблиц, а в большинстве
случаев
и трехзначных. Взамен
трех-
61

значных таблиц проще пользоваться 25-сантиметровой логарифмической линейкой,
50-сантиметровая- же линейка
даст
почти
такую
же точность, как четырехзначные
логарифмы.
При
выполнении приближенных вычислений
следует
руководствоваться сле-
дующими правилами, разработанными А. Н. Крыловым.
1. Точность данных и точность
результата
должны быть сообразованы с той прак-
тической потребностью, для которой вычисление производится.
2. При вычислениях, с приближенными числами надо в каждом из них удержи-
вать то число значащих
цифр,
которое необходимо для получения
результата
требуе-
мой
точности, помня, что всякая лишняя цифра лишь влечет бесполезную затрату
труда
и времени.
3. При вычислении по приближенным формулам величины площадей, объемов
и
т. д. надо брать такое число ординат, при котором точность формулы
соответствует
точности данных и требуемой точности результатов.
4. Малые изменения надо вычислять непосредственно, не вычисляя значений
самой величины. При вычислении ряда близких значений величины надо, вычислив
одно из них, для получения остальных вычислять к нему поправки.
5. Для всякого вычисления, в особенности когда тому же ряду действий должен
быть подвергнут целый ряд чисел, надо составить
схему,
располагая ее так, чтобы
сложение и вычитание производились ранее умножения, которое предшествовало бы
делению, и чтобы однообразный процесс действий не прерывался другим. При вы-
числении
в каждом частном
результате
надо удерживать лишь то число значащих
цифр,
которое требуется для окончательного
результата.
При
расчетах на вычислительных машинах результаты вычислений
следует
округлять, сообразуясь с практически требуемой точностью и с точностью исходных
данных.
Для оценки точности формул приближенного интегрирования приводятся
табл. 1.32 и 1.33, содержащие результаты выполненного В. Г. Власовым исследо-
вания
сравнительной точности различных правил. Названия правил даны в этих
таблицах сокращенно таким образом, что стоящая впереди цифра указывает коли-
чество ординат, следующая за ней буква является первой начальной буквой пра-
вила (Т — трапеций, Ч — Чебышева и С — Симпсона), значок
«штрих»
вверху
цифры,
означающей число ординат, указывает на замену крайней ординаты приведенной,
подстрочный индекс при цифре числа ординат указывает на количество добавочных
ординат.
Например,
наименование в табл. 1.32 правила 21'гТ для интегрирования по длине
соответствует
правилу трапеций с 21-й ординатой, причем две крайние ординаты за-
менены
приведенными и в каждой оконечности взяты две промежуточные ординаты
посередине крайних промежутков. Наименование 17
4
Т для интегрирования по длине
соответствует
правилу трапеций с 17-ю основными ординатами и четырьмя проме-
жуточными посередине
двух
крайних промежутков в каждой оконечности.
Наименование
124 для интегрирования по длине
соответствует
правилу Чебы-
шева с 12-ю ординатами, шестью носовыми и шестью кормовыми. Наименование 11
2
G
в
табл. 1.33 для интегрирования по высоте
соответствует
правилу Симпсона с 11-ю ос-
новными
ординатами и двумя добавочными в нижней части и т. д.
В табл. 1.32 и 1.33 приведены наибольшие погрешности, полученные в резуль-
тате
применения правил приближенного интегрирования для ряда кривых, выра-
жаемых уравнениями и похожих по своей форме на судостроительные кривые. Так
как
погрешность правила не зависит от масштаба кривой, а только от ее формы, то
главные размеры О
А
и ОВ изображенной на рис. 1.30 кривой могли быть приняты
равными единице. В таком
случае
"площадь кривой ОАВ численно равна ее
коэффи-
циенту полноты, а координаты центра тяжести ее и момента инерции являются от-
носительными координатами и относительными моментами инерции. В таблицах они
обозначены соответственно s, Xj, yf, i
x
, i
y
.
В табл. 1.32 приведены наибольшие относительные погрешности в процентах при
интегрировании по длине для величин s, 1>и i
y
и умноженные на 100 абсолютные по-
грешности относительных координат центра тяжести Xf и у/. Приведенные в послед-
нем
столбце таблицы суммы
всех
пяти погрешностей
могут
служить условной харак-
теристикой точности соответствующих правил. Поэтому правила в табл. 1.32 распо-
ложены в порядке возрастания этих сумм.
62

,
Таблица
1.32
Погрешности правил приближенного интегрирования (по длине)
пп
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27'
Наимено-
вание
правил
184
21
4
С
144
' 17
4
С
21
2
"Т
124
21 "Т
17
2
"Т
13
4
С
17"Т
21
4
Т
21С
21
2
Т
104
17
4
Т
17С
17
2
Т
13
2
"Т
13"Т
13
4
Т
13С
13
2
Т
21Т
94
17Т
74
13Т
S
0,1
0,2
0,2
0,2
0,2
0,2
0,3
0,3
0,4
0,4
0,5
0,5
0,6
0,4
0,7
0,7
0,8
0,5
0,6
1
1
i,'o'
1,2
1,2
0,3
1,6
0,7
2,5
Наибольшая
0
—н^-юо
0,0
0,1
0,1
0,1
0,1
0,2
0,0
0,2
0,1
0,0
. 0,2
0,1-
0,2
0,5
0,3
0,1
0,4
0,3
0,1
0,6
0,4
0,6
0,0
2,7
0,1
5,2
0,1
относительная
1
У
0,5
0,7
0,8
0,9
0,8
0,9
1,2
1,2
1,5
1,7
1,6
1,9
1,9
1,9
2,1
2,7
2,5
1,9
2,9
3,0
4,2
3,6
4,6
1,6
6,4
3,6
9,7
погрешность
&Xf 100
0,1
0,1
0,1
о!г
0,1
0,3
0,3
0,2
0,4
0,3
0,3
0,4
0,3
0,5
0,4 •
0,5
0,6
0,7
0,7
0,6
0,8
0,8
2,1
1,1
0,5
1,7
b.y
f
100
0,1
0,1
0,1
0,1
0,1
0,2
0,1
0,1
0,1
0,1
0,1
0,2
0,1
0,3
0,2
0,3
0,2
0,2
0,2
0,2
0,4
0,3
0,4
0,3
0,5
0,7
0,8
Сумма
погреш-
ностей
0,8
1,2
1,3
1,4
1,4
1,6
1,9
2,1
2,3
2,6
2,7
3,0
3,2
3,4
3,8
4,2
4,4
3,5
4,5
5,6
6,6
6,5
7,0
7,0
9,7
10,7
14,8
Первые шесть правил В. Г. Власов рекомендует в качестве пригодных для окон-
чательных расчетов, правила 7—17 рекомендуются им для предварительных расчетов
и
правила
18—27
совсем не рекомендуются, как не гарантирующие необходимой точ-
ности.
В
группу
нерекомендуемых
входит
также особенно распространенное правило
4ебышева с 9-ю ординатами, неточное в
отношении
момента инерции i
x
и коор-
динат Xf.
В табл. 1.33 приведены наибольшие
относительные погрешности при интегри-
ровании
по высоте для величин s и абсо-
лютные погрешности для величин Xf и yf.
Приведенные в последнем столбце суммы
погрешностей рассматриваются как услов-
ные характеристики точности соответ-
ствующих правил. Последовательность
расположения правил в табл. 1.33 соот-
ветствует
возрастанию этих сумм.
В качестве правила, пригодного для окончательных вычислений, В. Г. Власов
рекомендует первое, правила 2—9 рекомендуются им для предварительных расчетов,
а правила
10—25
совсем не рекомендуются.
Указанное разделение правил приближенного интегрирования по их пригод-
ности к расчетам является условным и предполагает, что ошибки не должны пре-
63
Рис.
1.30.

Таблица
1.33
Погрешность
правил приближённого интегрирования (по высоте)
№
ПП
1
2
3
4
6
'•
6
7
8
9
10
11
'
12
13
14
15
16
17
18
19
20
21
22
23
24
25
Наименова-
ние правил
1VT
И'Т
9!'Т
94
9'Т
•
74
64
64
11
а
С
7х'Т
7'Т
"
9
2
С
п
2
т
7
2
С
9
2
Т
9
Х
Т
ПС
9С
7
2
Т
7
а
Т
11Т
7С
9Т
7Т
Наибольшая
0,2
0,3
0,3
0,4
0,4
0,5
0,6
0,6
1,0
0,5
0,6
1,4
1,8
1,8
2,0
2,4
2,4
2,5
3,3
3,3
3,3
4,1
4,6
5,3
7,4
относительная
&x
f
100
0,2
0,3
0,3
0,2
0,4
0,3
0,3
0,3
0,5
0,6
0,7
0,7
0,9
0,9
1,0
1,2
1.2
1,3
1,7
1,8
1,8
2,2
2,5
2,9
4,0
погрешность
-
by
f
100
0,1
0,1
0,1
0,1
0,1
0,1
е,2
0,3
0,2
0,2
<
0,2
0,2
0,2
0,2
0.2
0,2
0,2
0,3
0,3
0,3
0,3
0,4
'
0,4
0,5
0,8
Сумма
погрешностей
0,5
0,7
0,7
0,7
0,9
0,9
1,1
1,2
1,7
1,3
1,5
2,3
2,9
2,9
3,2
3,8
3,8
4,1
5,3
5,4
5,4
6,7
7,5
8,7
12,2
. •
. I •
вышать установленные пределы
для
всех
исследованных кривых
и в с е х
элемен-
тов
их. В тех
случаях,
когда
на
практике
не
требуется вычисления всех-элементов,
или
если Понижены требования
к
точности расчета, суждение
о
пригодности правил
может изменяться.
В практических расчетах обычно применяется правило трапеций
с 21
равноот-
стоящим шпангоутом,
что
обеспечивает достаточную точность расчетов-
для
многих
типов
худов.
Однако
в
пределах этого правила возможны значительные колебания
в
величине допущенной погрешности
в
зависимости
от
способов применения приве-
денных ординат, степень использования которых должна быть различна
для
разных
типов судов.
~
1
Для
легких быстроходных
судов
или,
судов
с
ограниченной осадкой, строящихся
с соблюдением жесткой весовой дисциплины,
а
также
для
малоостойчивых
судов
точность расчетов должна быть выше,
и
применение приведенных ординат должно
быть проведено более тщательно
и
широко.
Для вспомогательных
и
грузовых
тихоходных
судов, имеющих большие запасы
остойчивости
без
ограничения осадки, точность расчета может быть уменьшена,
и
приведенные ординаты
могут
применяться
в
минимальной степени.
Большая
часть ручных расчетов может производиться
с
помощью 25-сантиметро-
вой логарифмической линейки, обеспечивающей достаточную
для
практических целей
точность.
При
проведении расчетов недопустимо округлять числа
и
необходимо
удер-
живать
все
значащие цифры, которые
могут
быть получены
на
логарифмической
ли-
нейке,
при
вычислении таких величин, которые
в
дальнейшем
входят
в
виде постоян-
ных множителей
в
расчет,
как,
например, величины
AL, Д7\
(Д7
1
)
2
и т. п.
64

§ 21.
ПРИМЕНЕНИЕ
ЭЛЕКТРОННЫХ
ВЫЧИСЛИТЕЛЬНЫХ
МАШИН
В
РАСЧЕТАХ
ПО
СТАТИКЕ
КОРАБЛЯ
Применение
электронных цифровых вычислительных машин (ЭЦВМ) создает
практически
неограниченные возможности быстрого и точного решения самых слож-
ных задач статики корабля. Использование этих возможностей связано с созданием
специальных «машинных» методе* вычисления элементов статики корабля, поскольку
разработанные ранее методы и практические приемы были созданы специально для
расчетов вручную.
Сложность и громоздкость расчетов статики корабля./особенно расчетов остой-
чивости и непотопляемости, привели к
тому,
что при создании традиционных руч-
ных методов вычислений принимались все возможные меры для упрощения рае-
четных схем, широко применялись промежуточные графические построения. Пре-
имущество уточненных ручных методов расчета вследствие возрастания их слож-
ности
нередко сводилось к нулю в связи с увеличением вероятности субъективных
ошибок
исполнителей.
Использование
ЭЦВМ не только создает условия Для применения более точ-
ных и совершенных расчетных схем, но и упрощает контроль полученных резуль-
татов, так как он практически сводится лишь к проверке правильности вводимо-
го в ЭЦВМ исходного материала.
Основные требования, предъявляемые к методам расчетов по статике ко-
рабля на ЭЦВМ,
могут
быть сформулированы следующим образом:
обеспечение необходимой точности расчетов;
по
возможности наименьшее количество необходимых для выполнения расчетов
исходных данных, которые должны быть общими для всего комплекса расчетов по
статике корабля;
практически
приемлемая и по возможности минимальная продолжительность вы-
полнения
расчетов на ЭЦВМ;
удобство
программирования, состоящее, в частности, в возможно большем одно-
образии расчетных зависимостей и в исключении необходимости применения проме-
жуточных графических построений в используемых методах расчетов;
исключение необходимости вмешательства операторов в работу ЭЦВМ во время
расчета, которое
ведет
к нерациональной потере машинного времени и увеличивает
возможность возникновения ошибок.
Из
этих требований, очевидно, главным
следует
считать первое, а осталь-
ные
должны выполняться при условии, что они не вступают в противоречие
с первым.
Вполне понятно, что
могут
быть разработаны различные вычислительные алго-
ритмы и программы для решения задач статики корабля. Поэтому в настоящем пара-
графе рассматриваются лишь основные вопросы, связанные с применяемыми в на-
стоящее время методами вычислений на ЭЦВМ. В связи с тем, что нельзя отдать
предпочтение какому-то одному типу ЭЦВМ или одному из алгоритмических языков,
тексты конкретных программ приводить здесь нецелесообразно. Описание ряда про-
грамм расчетов по статике корабля и вычислительных алгоритмов на языке
АЛГОЛ-60
можно найти в книге В. И. Брегмана «Решение задач статики корабля на ЭВМ».
Л., «Судостроение», 1966.
Выполнение любых расчетов по статике корабля на ЭЦВМ связано с определе-
нием
элементов погруженного объема и элементов действующей ватерлинии. Для
этого необходимо подготовить и ввести в память ЭЦВМ исходную информацию о форме
корпуса судна. Объем исходной информации должен быть достаточен для обеспече-
ния
необходимой точности расчетов и по возможности минимальным, так как машин-
ное
время, необходимое для выполнения расчетов, в той или иной степени пропор-
ционально
количеству исходных данных. Кроме того, исходная информация подго-
товляется вручную, и сокращение ее объема экономит время подготовки данных и
уменьшает вероятность появления субъективных ошибок исполнителя.
Основной
объем исходных данных о форме корпуса составляет информация
о
форме шпангоутных сечений. Контур сечения задается произвольно расположен-
ными
на нем точками, при назначении которых
следует
иметь в
виду,
что в дальнейшем
истинный
контур сечения
будет
заменен отрезками прямых
линий,
соединяющих
3 С. Н. Благовещенский, А. Н. Холодилин 65
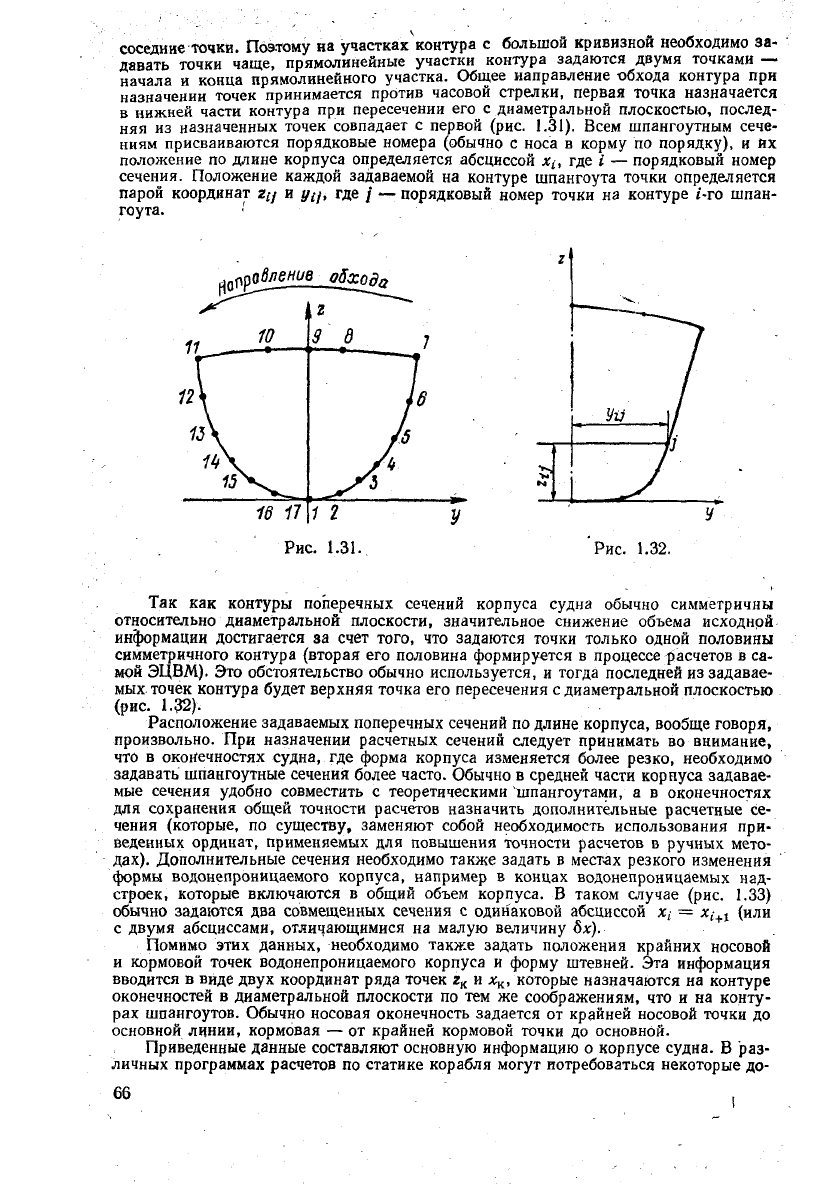
соседние точки. Поэтому на
участках
контура с большой кривизной необходимо за-
давать точки чаще, прямолинейные участки контура задаются двумя точками —
начала и конца прямолинейного участка. Общее направление
обхода
контура при
назначении
точек принимается против часовой стрелки, первая точка назначается
в
нижней части контура при пересечении его с диаметральной плоскостью, послед-
няя
из назначенных точек совпадает с первой (рис.
1.31).
Всем шпангоутным сече-
ниям
присваиваются порядковые номера (обычно с носа в корму по порядку), и их
положение по длине корпуса определяется абсциссой *,, где i — порядковый номер
сечения.
Положение каждой задаваемой на контуре шпангоута точки определяется
парой
координат гц и уц, где / — порядковый номер точки на контуре /-го шпан-
гоута.
•'
16 17 1 2
Рис.
1.31.
Рис.
1.32.
Так
как контуры поперечных сечений корпуса судна обычно симметричны
относительно диаметральной плоскости, значительное снижение объема исходной
информации
достигается за счет того, что задаются точки только одной половины
симметричного контура (вторая его половина формируется в процессе расчетов в са-
мой
ЭЦВМ). Это обстоятельство обычно используется, и
тогда
последней из задавае-
мых точек контура
будет
верхняя точка его пересечения с диаметральной плоскостью
(рис.
1.32).
Расположение задаваемых поперечных сечений по длине корпуса, вообще говоря,
произвольно.
При назначении расчетных сечений
следует
принимать во внимание,
что в оконечностях судна, где форма корпуса изменяется более резко, необходимо
задавать шпангоутные сечения более часто. Обычно в средней части корпуса задавае-
мые сечения удобно совместить с теоретическими шпангоутами, а в оконечностях
для сохранения общей точности расчетов назначить дополнительные расчетные се-
чения
(которые, по
существу,
заменяют собой необходимость использования при-
веденных ординат, применяемых для повышения точности расчетов в ручных мето-
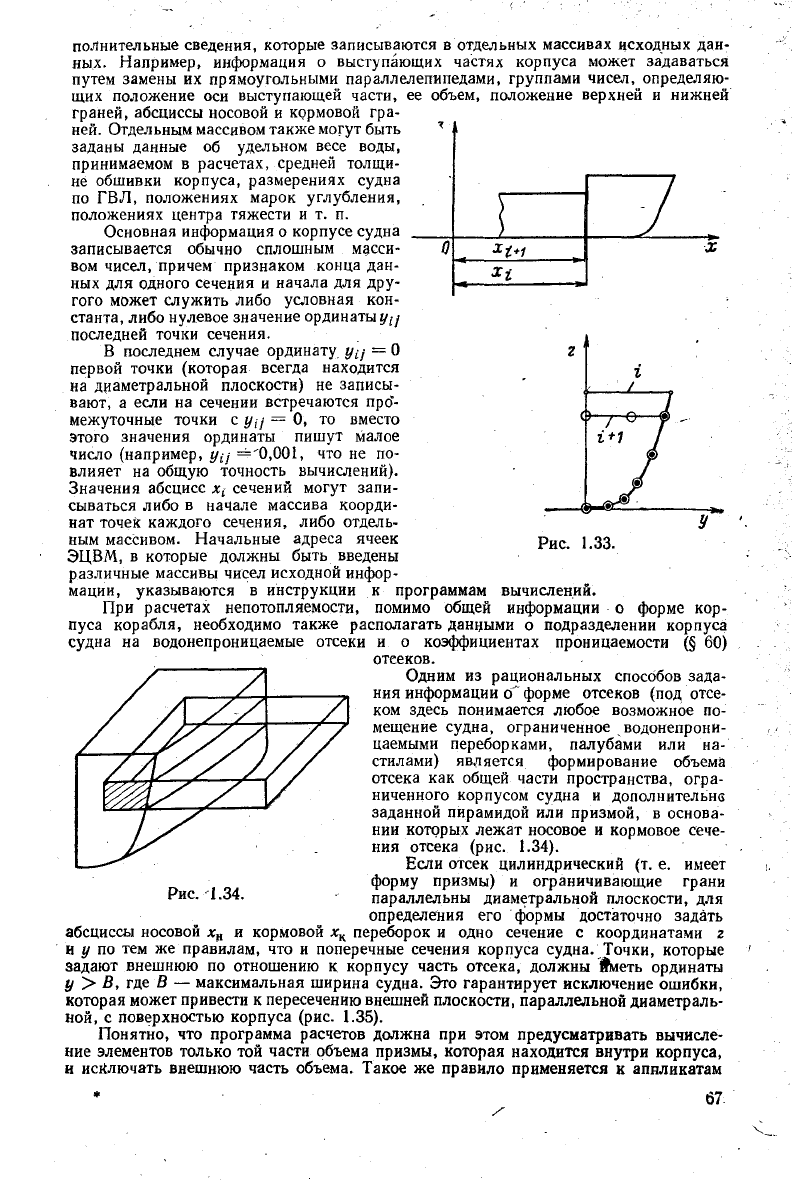
дах). Дополнительные сечения необходимо также задать в местах резкого изменения
формы
водонепроницаемого корпуса, например в концах водонепроницаемых над-
строек, которые включаются в общий объем корпуса. В таком
случае
(рис. 1.33)
обычно задаются два совмещенных сечения с одинаковой абсциссой x
t
= х,
+1
(или
с двумя абсциссами, отличающимися на
малую
величину 6х).
Помимо
этих данных, необходимо также задать положения крайних носовой
и
кормовой точек водонепроницаемого корпуса и форму штевней. Эта информация
вводится в виде
двух
координат ряда точек г
к
и х
к
, которые назначаются на контуре
оконечностей в диаметральной плоскости по тем же соображениям, что и на конту-
рах шпангоутов. Обычно носовая оконечность задается от крайней носовой точки до
основной
линии, кормовая — от крайней кормовой точки до основной.
Приведенные данные составляют основную информацию о корпусе судна. В раз-
личных программах расчетов по статике корабля
могут
потребоваться некоторые до-
66
Xi
J
Рис.
1.33.
поЛнительные сведения, которые записываются
в
отдельных массивах исходных
дан-
ных. Например, информация
о
выступающих частях корпуса может задаваться
путем замены
их
прямоугольными параллелепипедами, группами чисел, определяю-
щих положение
оси
выступающей части,
ее
объем, положение верхней
и
нижней
граней, абсциссы носовой
и
кормовой
гра-
ней.
Отдельным массивом также
могут
быть
заданы данные
об
удельном весе воды,
принимаемом
в
расчетах,
средней толщи-
не
обшивки корпуса, размерениях судна
по
ГВЛ,
положениях марок углубления,
положениях центра тяжести
и т. п.
Основная
информация
о
корпусе судна
записывается обычно сплошным масси-
вом чисел, причем признаком конца
дан-
ных
для
одного сечения
и
начала
для дру-
гого может служить либо условная
кон-
станта, либо нулевое значение ординаты
уц
последней точки сечения.
В последнем
случае
ординату
уц =
О
первой точки (которая
всегда
находится
на
диаметральной плоскости)
не
записы-
вают,
а
если
на
сечении встречаются про*-
межуточные точки
с уц = 0, то
вместо
этого значения ординаты пишут малое
число (например,
уц
='0,001,
что не по-
влияет
на
общую точность вычислений).
Значения
абсцисс
jt,
сечений
могут
запи-
сываться либо
в
начале массива коорди-
нат точек каждого сечения, либо отдель-
ным
массивом. Начальные адреса ячеек
ЭЦВМ,
в
которые должны быть введены
различные массивы чисел исходной инфор-
мации,
указываются
в
инструкции
к
программам вычислений.
При
расчетах непотопляемости, помимо общей информации
о
форме
кор-
пуса корабля, необходимо также располагать данными
о
подразделении корпуса
судна
на
водонепроницаемые отсеки
и о
коэффициентах проницаемости
(§ 60)
отсеков.
Одним
из
рациональных способов зада-
ния
информации
о~~
форме отсеков
(под
отсе-
ком
здесь понимается любое возможное
по-
мещение судна, ограниченное водонепрони-
цаемыми переборками, палубами
или на-
стилами) является формирование объема
отсека
как
общей части пространства, огра-
ниченного
корпусом судна
и
дополнительно
заданной пирамидой
или
призмой,
в
основа-
нии
которых лежат носовое
и
кормовое сече-
ния
отсека
(рис.
1.34).
Если отсек цилиндрический
(т. е.
имеет
форму призмы)
и
ограничивающие грани
параллельны диаметральной плоскости,
для
определения
его
формы достаточно задать
абсциссы носовой
х„ и
кормовой
х
к
переборок
и
одно сечение
с
координатами
г
и
у по тем же
правилам,
что и
поперечные сечения корпуса судна. Точки, которые
задают внешнюю
по
отношению
к
корпусу часть отсека, должны Иметь ординаты
у
> В, где В —
максимальная ширина судна.
Это
гарантирует исключение ошибки,
которая может привести
к
пересечению внешней плоскости, параллельной диаметраль-
ной,
с
поверхностью корпуса (рис.
1.35).
Понятно,
что
программа расчетов должна
при
этом
предусматривать вычисле-
ние элементов только
той
части объема призмы, которая
находится внутри корпуса,
и исключать внешнюю часть объема. Такое
же правило применяется к аппликатам
*
67
Рис.
1.34.
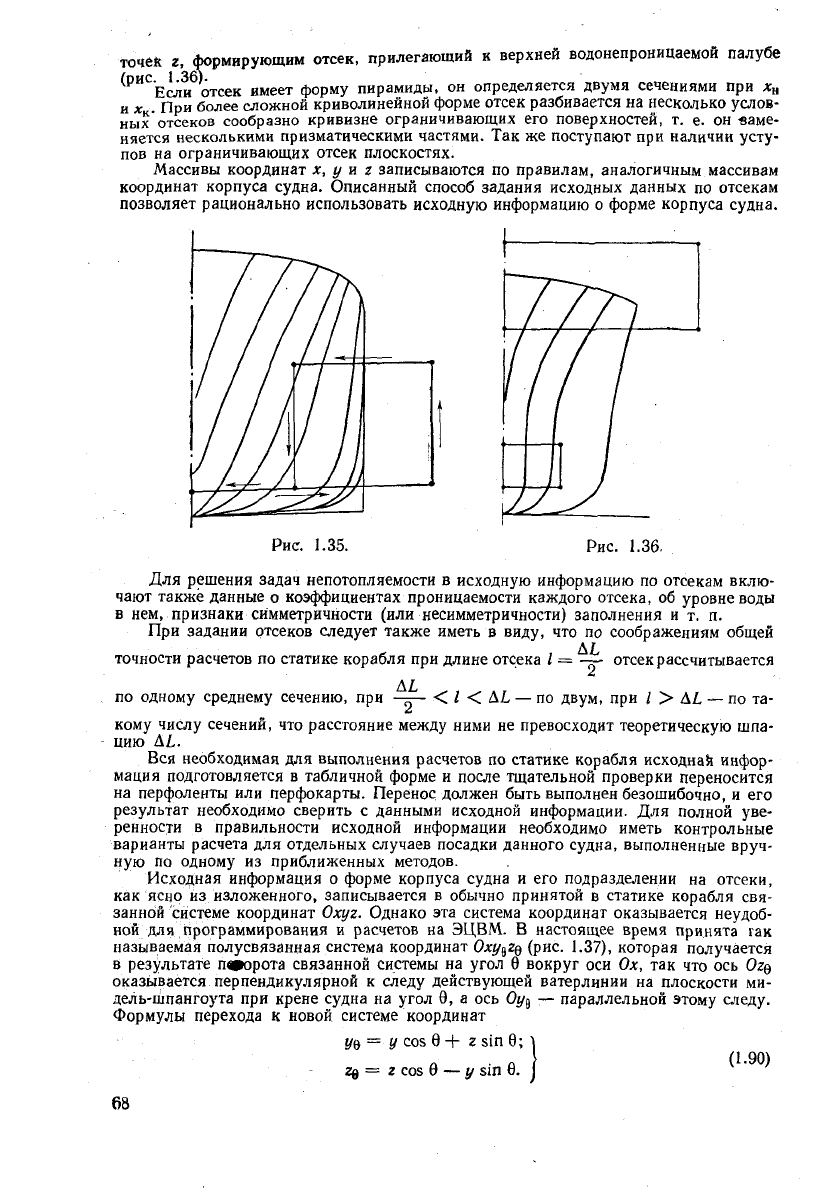
точек г, формирующим отсек, прилегающий к верхней водонепроницаемой
палубе
Если отсек имеет форму пирамиды, он определяется двумя сечениями при х
н
и
х При более сложной криволинейной форме отсек разбивается на несколько услов-
ных отсеков сообразно кривизне ограничивающих его поверхностей, т. е. он заме-
няется
несколькими призматическими частями. Так же поступают при наличии
усту-
пов
на ограничивающих отсек плоскостях.
Массивы координат х, у и г записываются по правилам, аналогичным массивам
координат корпуса судна. Описанный способ задания исходных данных по отсекам
позволяет рационально использовать исходную информацию о форме корпуса судна.
Рис.
1.35.
Рис.
1.36.
Для решения задач непотопляемости в исходную информацию по отсекам вклю-
чают
также данные о коэффициентах проницаемости каждого отсека, об уровне воды
в
нем, признаки симметричности (или несимметричности) заполнения и т. п.
При
задании отсеков
следует
также иметь в
виду,
что по соображениям общей
точности расчетов по статике корабля при длине отсека / = -—- отсек рассчитывается
по
одному среднему сечению, при -=— < I < AL — по
двум,
при / > AL — по та-
кому числу сечений, что расстояние
между
ними не превосходит теоретическую шпа-
цию AL.
Вся необходимая для выполнения расчетов по статике корабля исходная инфор-
мация
подготовляется в табличной форме и после тщательной проверки переносится
на
перфоленты или перфокарты. Перенос должен быть выполнен безошибочно, и его
результат
необходимо сверить с данными исходной информации. Для полной уве-
ренности в правильности исходной информации необходимо иметь контрольные
варианты расчета для отдельных
случаев
посадки данного судна, выполненные
вруч-
ную по одному из приближенных методов.
Исходная информация о форме корпуса судна и его подразделении на отсеки,
как
ясно из изложенного, записывается в обычно принятой в статике корабля свя-
занной
системе координат
Oxyz.
Однако эта система координат оказывается неудоб-
ной
для программирования и расчетов на ЭЦВМ. В настоящее время принята гак
называемая полусвязанная система координат
Оху^г^
(рис.
1.37),
которая получается
в
результате
пвюрота связанной системы на
угол
9 вокруг оси Ох, так что ось
OZQ
оказывается перпендикулярной к
следу
действующей ватерлинии на плоскости ми-
дель-шпангоута при крене судна на
угол
9, а ось 0у
9 :
— параллельной этому
следу.
Формулы перехода к новой системе координат
i/e = у cos 9 + г sin f
г%
= г cos 9 — у sin б. '
68

В системе координат
Охуг
посадка судна определяется тремя параметрами, пред-
ложенными В. Г. Власовым (§ 2). Связь
между
параметрами посадки в новой полу-
связанной
системе координат с прежними определится следующими простыми за-
висимостями:
Г
е
= Т cos в;
cos
(1.91)
Параметр в остается тем же (§ 2).
Переход к новой, «машинной» системе координат осуществляется в самой ЭЦВМ,
и
на подготовку исходной информации для расчетов это обстоятельство не влияет.
Вычисления же проводятся в новой си-
стеме, и поэтому расчетные зависимо- •
сти
будут
иметь несколько иной вид.
Так,
объем подводной части судна при
посадке его по произвольную ватерли-
нию
(§ 2 или 17) вычисляется по
формуле
V =
J
Ji/
e
n&e^-J
J y^ <fa
e
Лс.
(1.92)
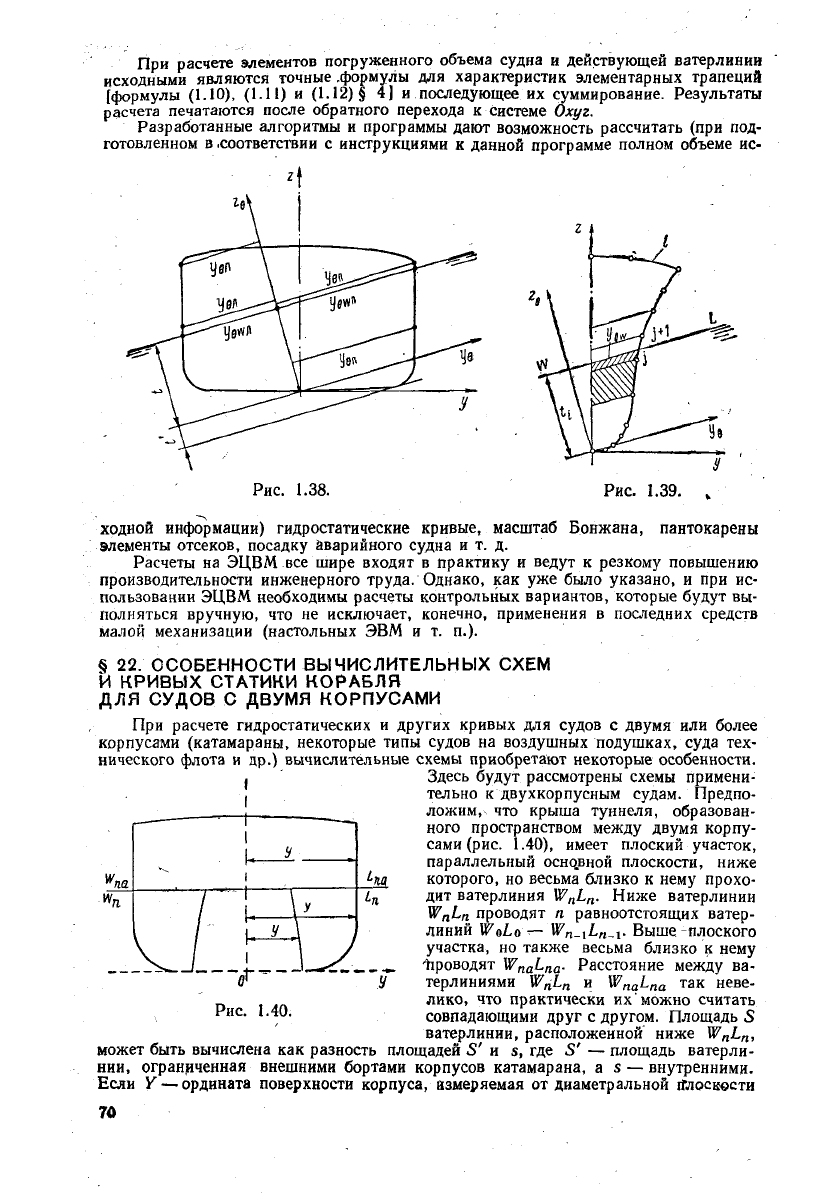
где ординаты i/g
n
и (/
вл
определяются
в
соответствии с обозначениями
рис.
1.38. При интегрировании попе-
речные сечения корпуса разбиваются на ряд элементарных трапеций отрезками
прямых, проходящими через заданные на контуре сечения точки. Ординаты дей-
ствующей ватерлинии y$
w
находятся интерполяцией при
tt = Tf,+ x
t
tg яре-
(1.93)
Для определения площади действующей ватерлинии
тогда
имеем
=
J
t/ешп dx —
j
у
ви)л
dx.
• (1.94)
Положение любой элементарной трапеции относительно ватерлинии (три случая
на
рис. 1.39) определяется с
учетом
величины t[ — цц и знаков разностей t{ —
2
flt
/
и
ti —
Z
9i/+i"
так
>
для
трапеции, находящейся целиком под действующей ватер-
линией,
выполняются условия
sign
(ti — z
uj
) =
sign
(ti — z
ei/+1
);
U
—
гвИ
^ °-
(1.95)
Для трапеции, находящейся над ватерлинией, второе условие
(1.95)
изменится на
ti-z
w
<Q.
(1.96)
Для пересекаемой ватерлинией трапеции выполняется одно неравенство
sign
(t
t
— z
e
,y) ф
sign
(t
t
— z
e
,7
+1
).
(1.97)
Знак
sign
здесь обозначает единицу со знаком величины, находящейся в скобках.
Если выполняется последнее из написанных условий, т. е. условие (1.97), то в рас-
чете
учитываются элементы погруженной части трапеции, образованной отрезками
ординат у
в
ц- и </е
1Ш
, причем
(1.98)
69
При
расчете элементов погруженного объема судна и действующей ватерлинии
исходными являются точные .формулы для характеристик элементарных трапеций
[формулы (1.10),
(1.11)
и
(1.12)
§ 4] и последующее их суммирование. Результаты
расчета печатаются после обратного перехода к системе
Охуг.
Разработанные алгоритмы и программы
дают
возможность рассчитать (при под-
готовленном в .соответствии с инструкциями к данной программе полном объеме ис-
Рис.
1.38.
Рис.
1.39.
ходной информации) гидростатические кривые, масштаб Бонжана, пантокарены
элементы отсеков, посадку аварийного судна и т. д.
Расчеты на ЭЦВМ все шире
входят
в практику и
ведут
к резкому повышению
производительности инженерного
труда.
Однако, как уже было указано, и при ис-
пользовании ЭЦВМ необходимы расчеты контрольных вариантов, которые
будут
вы-
полняться
вручную, что не исключает, конечно, применения в последних средств
малой механизации (настольных ЭВМ и т. п.).
§ 22. ОСОБЕННОСТИ ВЫЧИСЛИТЕЛЬНЫХ СХЕМ
И КРИВЫХ СТАТИКИ КОРАБЛЯ
ДЛЯ
СУДОВ С ДВУМЯ КОРПУСАМИ
При
расчете гидростатических и
других
кривых для
судов
с двумя или более
корпусами (катамараны, некоторые типы
судов
на воздушных подушках,
суда
тех-
нического флота и др.) вычислительные схемы приобретают некоторые особенности.
Здесь
будут
рассмотрены схемы примени-
тельно к двухкорпусным
судам.
Предпо-
ложим,, что крыша туннеля, образован-
ного пространством
между
двумя корпу-
сами (рис.
1.40),
имеет плоский участок,
параллельный основной плоскости, ниже
которого, но весьма близко к нему прохо-
дит ватерлиния W
n
L
n
. Ниже ватерлинии
W
n
Ln
проводят п равноотстоящих ватер-
линий
WoLo'r—
W
n
_
l
L
n
_
l
. Выше-плоского
участка, но также весьма близко к нему
Проводят W
na
L
na
. Расстояние
между
ва-
терлиниями
W
n
L
n
и W
n
qL
na
так неве-
лико,
что практически их можно считать
совпадающими
друг
с
другом.
Площадь S
ватерлинии, расположенной" ниже W
n
L
n
,
может быть вычислена как разность площадей S' и s, где S' — площадь ватерли-
нии,
ограниченная внешними бортами корпусов катамарана, as — внутренними.
Если К —ордината поверхности корпуса, измеряемая от диаметральной гГлосвости
70
Рис.
1.40.
