Благовещенский С.Н., Холодилин А.Н. Справочник по статике и динамике корабля. Динамика корабля. Том 2

Подождите немного. Документ загружается.

глава

БОКОВАЯ КАЧКА СУДНА

ОБЩИЙ

СЛУЧАЙ КАЧКИ СУДНА,

РАСПОЛОЖЕННОГО

ЛАГОМ К ВОЛНЕ

Примем

систему координат в соответствии с ряс. 3.1. Систему дифференциаль-

ных уравнений движения запишем в виде

+ hi) 9 + bj + DM +

+ 6

T]g

где D — водоизмещение судна; S — площадь ГВЛ; h — поперечная метацентриче-

ская

высота; ^ и b

j — присоединенные массы и коэффициенты сопротивления;

— поправочные коэффициенты. •

В системе (3.1) уравнение вертикальной »^^ /

качки

независимо от остальных

двух.

'^""""-^

В дальнейшем,

следуя

С. Н. Благове-

щенскому, положим _^

В соответствии с рекомендациями А. В. Гера-

симова, примем

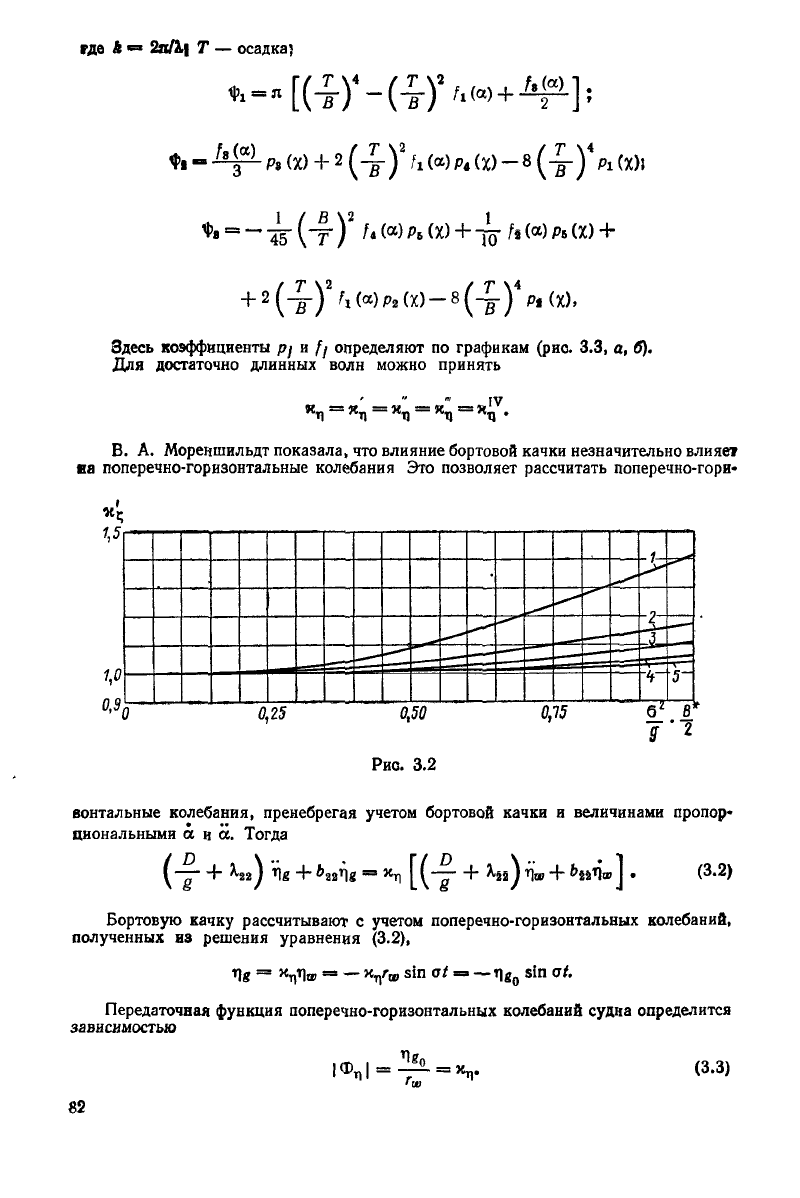
Согласно рекомендации В А Мор'еншильдт

Kj =* xZ, а х^ определяется по графику

(рис

3.2) в функции коэффициента kB*l2,

где k — волновое число, а В* = (В

1о

+ В

)/3. Здесь В

, В

и В

1ъ

ширина

судна на 5, 10 и 15 теоретических шпангоутах соответственно. С Н. Благове-

щенский

рекомендует применять зависимость х^ = Xg = щ_.

Редукционные коэффициенты Xj. х^ н х-_ определяются в соответствии с реко-

мендациями

§ 7.

В. В. Луговский предлагает принимать

Рис.

3.1

где ft •=» 2яА| Г — осадка;

Р» (X) + 2

(-J)

(«) Р« (X) -8 (^-

- ^ (-?" )

h («) Р» (X) + -jj /i («) Рб (X)

(

Т \2

Здесь коэффициенты р/ и /у определяют по графикам (рис. 3.3, а, б).

Для достаточно длинных волн можно принять

[у

В. А. Мореншильдт показала, что влияние бортовой качки незначительно влияет

ва поперечно-горизонтальные колебания Это позволяет рассчитать поперечно-гори-

1,0

0,8,

0,25

0,50

Рис.

3.2

0,75

*—-

^-*

••' ^

——

.——--

— '—

.—"

•

-7-

-2-

=i-

з^:

"*-

——

1— —

-т—

В*

7'"*

вонтальные колебания, пренебрегая

учетом

бортовой качки и величинами пропор-

циональными

а и а. Тогда

(3.2)

Бортовую качку рассчитывают с

учетом

поперечно-горизонтальных колебаний,

полученных из решения уравнения (3.2),

t]g =

x^Tia,

= — Х-Гц, sin ot ^

"~~Лйп

*^'*

Передаточная функция поперечно-горизонтальных колебаний судна определится

зависимостью

|Ф«|

= ^

- = х

,. (3.3)

При

сделанных допущениях поперечно-горизонтальные колебания центра

тяжести

судна

происходят в одной фазе с горизонтальными колебаниями частиц

воды с амплитудой v^

Расчеты, выполненные В. А. Мореншильдт, показывают, что вычисления по

формуле (3.2) приводят к завышению амплитуды примерно на 15% и к ошибкам по

фазе до 10°, что вполне допустимо при

инженерных

расчетах

качки

судна.

^ $

Под

действием достаточно длинных

волн поперечно-горизонтальные колебания

центра тяжести

судна

близки к горизон-

тальным составляющим движения частиц

волны,

так что приближенно можно

считать, что

0.В

0,6

Практически

это приводит к равенству

коэффициентов

0,2

Oft 0,9 %

о,

o,s

ол

0,1

а>

Рис.

3.3

Движение центра тяжести

судна,

рас-

положенного лагом к волне, описывается

системой уравнений вертикальной качки и поперечно-горизонтальных колебаний

(3-4)

влв в приведенном виде после деления уравнения (3.4) на коэффициент вря второй

вроизводной

g'g +

+ at%

= r

{xj- (®l — ?У) cos at —

xj.2v

sin at), (3.5)

где

"83

Решение

уравнения (3.5) имеет вид

где

- <7

) -xj (m

- о

)]

ej =

arctg

Квадрат передаточной функции вертикальной качки

(3.7)

Систему уравнений движения центра тяжести запишем в виде

—х^гд,

sin o<;

"с

(

с —

Для длинной волны к -* оо, eg

->•

0 система уравнений переходит в уравнение

окружности с центром в центре тяжести судна и радиусом r

(в этом

случае

все ре-

дукционные коэффициенты стремятся к единице). Этот случай

соответствует

случаю

малого поплавка на длинной волне, когда кажущиеся силы веса все время направ-

лены нормально к волне. На подошве волны кажущийся вес больше, а на вершине —

меньше веса поплавка. На более коротких волнах, вблизи резонанса, траектория

центра тяжести судна приобретает форму овала, вытянутого по вертикали.

Ф.

Тасаи предложил учитывать при качке судна, расположенного лагом к вол-

иению,

рыскание.

результате

имеет место система дифференциальных уравнений бортовой

качки,

поперечно-горизонтальных колебании и рыскания. Система, предложен-

ная

Ф. Тасаи, имеет вид

Ыг + *w)

Vx + Я.

) в + b

$ +

DhQ

+ К

щ + 6

^ +

А,

4в

4вФ

= М

где Dig — масса судна; J

— момент инерции судна относительно вертикальной оси

(рыскания);

— момент инерции судна относительно продольной оси (бортовая

качка).

Гидродинамические коэффициенты определяются по гипотезе плоских сечений

равны

^•22

I ^22 dx; ...; Xgf, = I A

6(i

dx;

L L

Ьц

= J

622

dx;

...; b

= J b'

dx,

L L

где

cWt) t?_ dm'

dm'

"'•ti

4- • -L [

Nn {

0,G)

)

где

К, = Ч К (/„ -

- х,о А

{„'(/,,

где о — скорость судна; т' — двухразмерная присоединенная масса для поперечно-

горизонтальных колебаний; Л^ — двухразмерный коэффициент демпфирования для

поперечно-горизонтальных колебаний; /,, — плечо момента инерции около оси х,

проходящей через точку О

, в результате поперечно-горизонтальных колебаний;

— то же демпфирующих сил; 1'

— двухразмерный присоединенный момент

инерции

относительно оси х, проходящей через центр тяжести судна; а

— кажу-

щаяся

частота; О

ч- точка пересечения плоскости окрашенной ватерлинии и

вер»

тикальной

прямой, проходящей через центр тяжести судна, на тихой воде; O

G —

вертикальное расстояние между G и О

Для вычисления коэффициента демпфирования бортовой качки с учетом ско-

рости движения судна Ф. Тасаи предложил следующую формулу:

*и = *к И + 0,8 (1 -

10Fr

)

(ш

/а

)

где

=VDh/(J

)

;

cog — собственная частота бортовых колебаний;

= aVg = 2я/К;

— коэффициенты, определяемые по кривой "затухающих колебаний;

— амплитуда волны; 9

— амплитуда бортовой качки судна; J

+ к

—

эффек-

тивный

момент инерции относительно оси, проходящей через G.

§ 9. ЛИНЕЙНАЯ

БОРТОВАЯ

КАЧКА

СУДНА

НА РЕГУЛЯРНОМ ВОЛНЕНИИ

Полное

уравнение бортовой качки на регулярном волнении в абсолютных коор-

динатах имеет вид

(У, + Я«) 9 + b

b + DhQ = D

Уравнение в относительных координатах, если понимать под относительным

углом крена

угол

крена относительно действующего уровня воды ф = 9 — а, гдш

а —

угол

волнового склона, имеет вид

(Jx + V) О + bj> +

Dhb=

— Jx^a.

В инженерных расчетах бортовой качки часто применяется укороченное урав-

нение

бортовой качки (без

учета

гидродинамических компонентов)

В приведенном виде эти уравнения запишем в следующей форме!

+ 2v

6 +

а>1&

= а

[(ш£ - ^а

) sin at + 2v

a cos at]; (3.8)

= a-

-^— a

sin at; (3.9)

+ ш^е = a

a>Q sin at,

(3.10)

где 2va =

-=—**г

линейный коэффициент сопротивления бортовой качки;

*°e

"7—п квадрат свободной частоты бортовых колебаний судна; оа =

• * "Г

4«

А.

—;—р^т относительный коэффициент присоединенного момента инерции;

•>Х

-Г

т —

о — приведенная амплитуда волнового склона, a = a

sin at.

Общий интеграл этих уравнений можно написать как

сумму

общего решения

однородного дифференциального уравнения (правая часть равна нулю) и частного

решения.

Общее решение для

всех

трех

уравнений одинаково

= е~

(cj cos n

t+ с

sin л

0 + 6,

где в — частное решение; га

=|^а>§

— vg; с

и с

— постоянные интегрирования,

определяемые начальными условиями.

Общее решение однородного уравнения описывает свободные колебания судна,

которые происходят с частотой ng на тихой воде и вследствие наличия сопротивле-

ния

(vg> 0) интенсивно

затухают.

Частное решение определяет вынужденные ко-

лебания.

Как показывают наблюдения, на нерегулярном волнении свободные коле-

бания

также интенсивно погашаются (нерегулярное волнение рассматривается кан

случайный стационарный процесс), поэтому при рассмотрении качки судна на вол-

нении

достаточно ограничиться вычислением только вынужденных колебаний судна

можно не рассматривать свободные колебания.

Частное решение'укороченного уравнения бортовой качки

(3.10)

6 = 6

sin (at — е

где

m°>e

(ш§

—

)

4vga

(3.11)

Частное решение дифференциального уравнения бортовой качки в абсолютных

координатах (3.8)

6 = 6

sin (at + о

— е

где

" " *~"

(3.12)

) — S

= arctg

arctg -~-

Частное решение уравнения в относительных координатах (3.9)

•&„,

sin (at — e

где

tge

= arctg

2ve

Здесь ж = a/coe; 2ц

= 2v

/a>

— безразмерный коэффициент гашения качки.

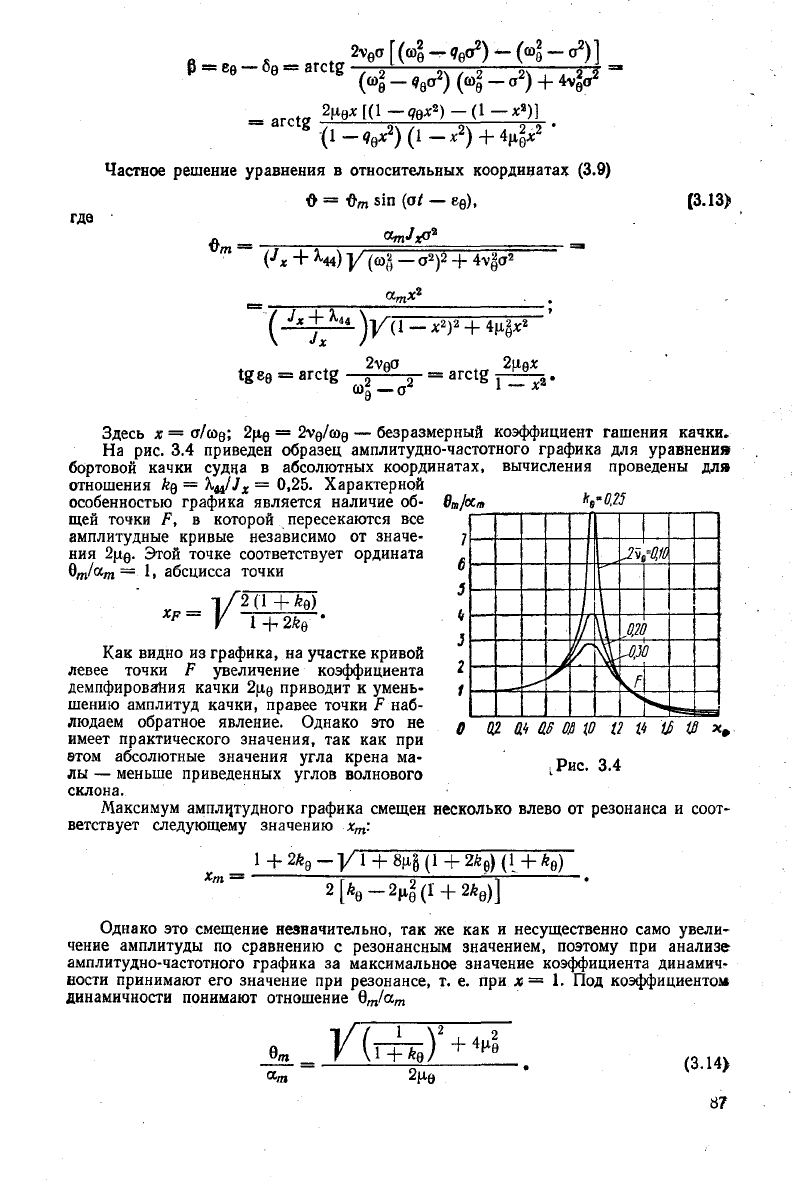
На

рис. 3.4 приведен образец амплитудно-частотного графика для уравнение

бортовой качки судна в абсолютных координатах, вычисления проведены для

отношения

= ^u/J

— 0,25. Характерной

особенностью графика является наличие об-

ft»/oc

ffl

*,-##

щей

точки F, в которой пересекаются все

амплитудные кривые независимо от значе-

ния

2[*0. Этой точке

соответствует

ордината

§т!

— 1. абсцисса точки

2 (1 + fee)

2% '

к\

«а

Как

видно из графика, на участке кривой

левее точки F увеличение коэффициента

демпфирования

качки 2[г

приводит к умень-

шению амплитуд качки, правее точки F наб-

людаем обратное явление. Однако это не

имеет практического значения, так как при

этом абсолютные значения

угла

крена ма-

лы — меньше приведенных

углов

волнового

склона.

Максимум амплцтудного графика смещен несколько влево от резонанса и соот-

ветствует

следующему

значению х

а*

ее

он

ю и и w ш

PHC.

3.4

2Ц (1

[*9-

Однако это смещение незначительно, так же как и несущественно само увели-

чение амплитуды по сравнению с резонансным значением, поэтому при анализе

амплитудно-частотного графика за максимальное значение коэффициента динамич-

ности принимают его значение при резонансе, т. е. при х = 1. Под коэффициентом

динамичности понимают отношение

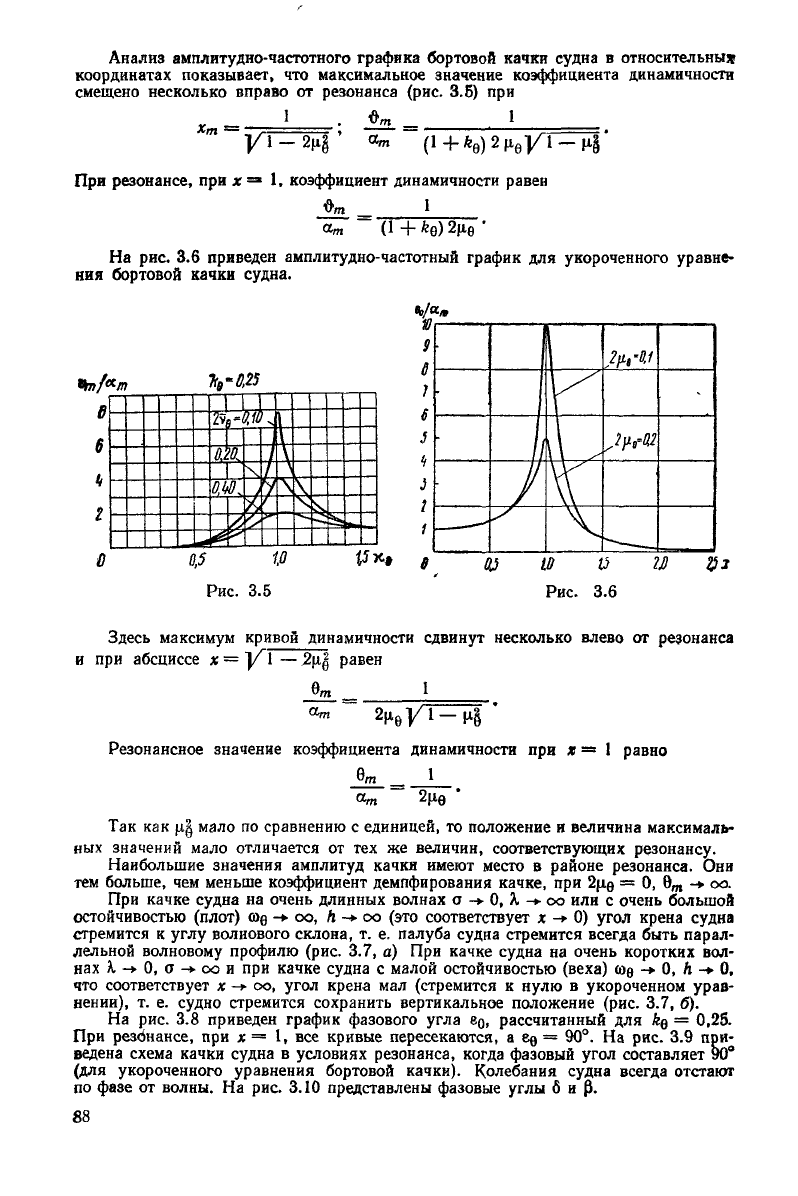
Анализ амплитудно-частотного графика бортовой качки судна в относительны»

координатах показывает, что максимальное значение коэффициента динамичности

смещено несколько вправо от резонанса (рис. 3.5) при

yi-2|lg

«m (1+ft,

При

резонансе, при х = 1, коэффициент динамичности равен

«т (1

На

рис. 3.6 приведен амплитудно-частотный график для укороченного уравне-

ния

бортовой качки судна.

,«

дед

ч,

г"

0,5 W

Рис.

3.5

•

"~-——

10 У

Рис.

3.6

Здесь максимум кривой динамичности сдвинут несколько влево от резонанса

при абсциссе * = |Л1 — 2ц| равен

8т

«m

2ц

у1-1

Резонансное

значение коэффициента динамичности при х = 1 равно

Так

как (х| мало по сравнению с единицей, то положение и величина максималь-

ных значений мало отличается от тех же величин, соответствующих резонансу.

Наибольшие значения амплитуд качки имеют место в районе резонанса. Они

тем больше, чем меньше коэффициент демпфирования качке, при 2це = 0, 9

-*• оо.

При

качке судна на очень длинных волнах а -»• О, Я

-»•

со или с очень большой

ОСТОЙЧИВОСТЬЮ (ПЛОТ)

сое -*

ОО,

->• ОО (ЭТО

соответствует

д:

->•

угол

крена судна

стремится к

углу

волнового склона, т. е. палуба судна стремится

всегда

быть парал-

лельной волновому профилю (рис. 3.7, а) При качке судна на очень коротких вол-

нах к -* 0, а

-»•

оо и при качке судна с малой остойчивостью

(веха)

cog -> О, А -• О,

что

соответствует

х -* оо,

угол

крена мал (стремится к нулю в укороченном урав-

нении),

т. е. судно стремится сохранить вертикальное положение (рис. 3.7, б).

На

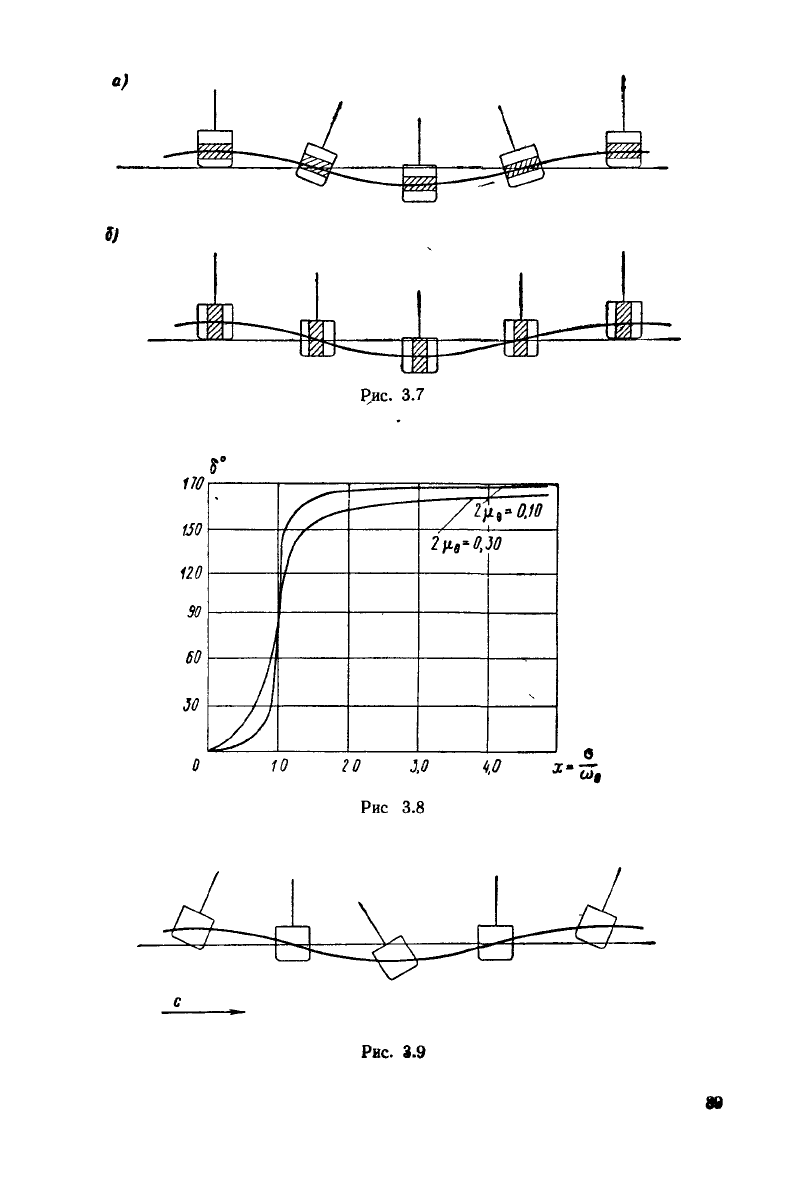
рис. 3.8 приведен график фазового

угла

во, рассчитанный для к$ = 0,25.

При

резбнансе, при х = 1, все кривые пересекаются, а 89 = 90°. На рис. 3.9 при-

ведена

схема

качки судна в условиях резонанса, когда фазовый

угол

составляет 90°

(для укороченного уравнения бортовой качки). Колебания судна

всегда

отстают

по

фазе от волны. На рис. 3.10 представлены фазовые

углы

6 и р\

110

150

120

—

/£)i

*OJO

2flg'-0,,

10 20 3,0

Рис

3.8

U),

Рис.

3.9

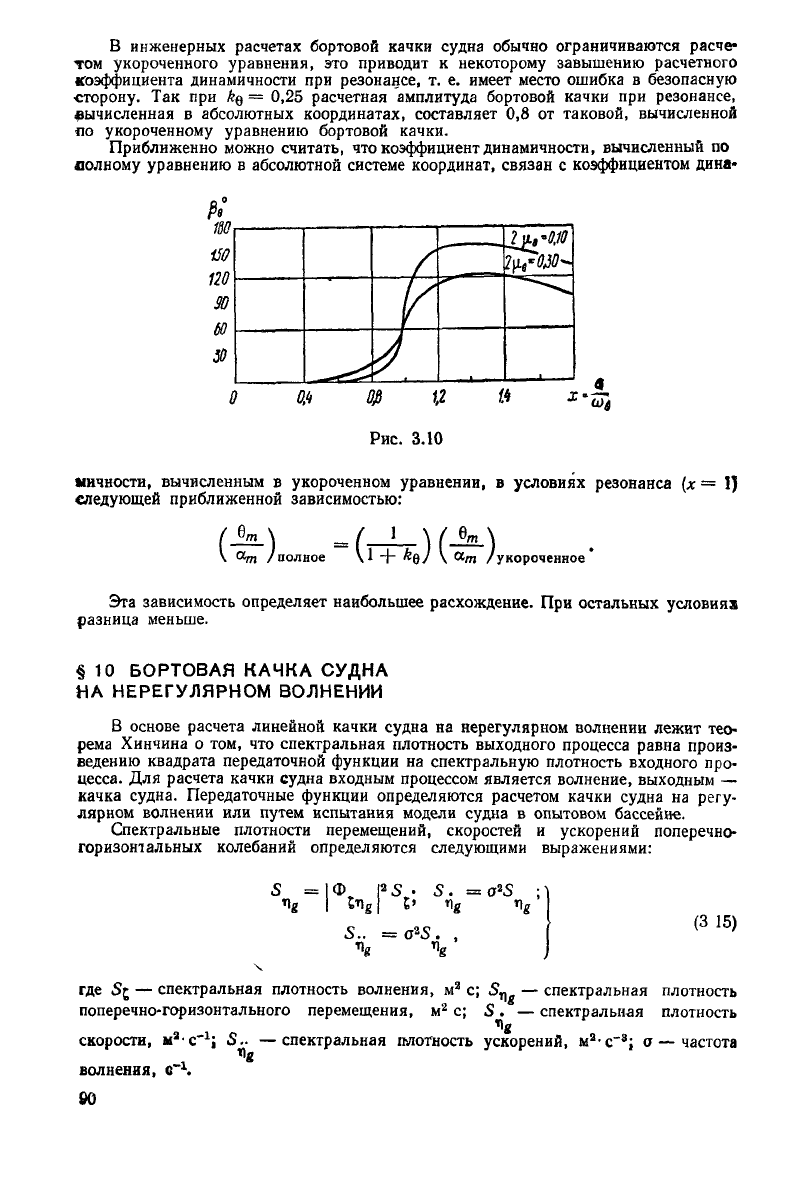
В инженерных расчетах бортовой качки судна обычно ограничиваются расче-

том укороченного уравнения, это приводит к некоторому завышению расчетного

коэффициента

динамичности при резонансе, т. е. имеет место ошибка в безопасную

•сторону. Так при k$ = 0,25 расчетная амплитуда бортовой качки при резонансе,

вычисленная в абсолютных координатах, составляет 0,8 от таковой, вычисленной

по

укороченному уравнению бортовой качки.

Приближенно

можно считать, что

коэффициент

динамичности, вычисленный по

полному уравнению в абсолютной системе координат, связан с коэффициентом дина-

ISO

150

ПО

Jjh'OJO

2^-OJO-

Рис.

3.10

мичности,

вычисленным в укороченном уравнении, в условиях резонанса (х = V)

следующей приближенной зависимостью:

полное \ 1 + HQ) \ a

/укороченное '

Эта зависимость определяет наибольшее расхождение. При остальных условиях

разница

меньше.

§ 10 БОРТОВАЯ КАЧКА СУДНА

НА НЕРЕГУЛЯРНОМ ВОЛНЕНИИ

В основе расчета линейной качки судна на нерегулярном волнении лежит тео-

рема Хинчина о том, что спектральная плотность выходного процесса равна произ-

ведению квадрата передаточной функции на спектральную плотность входного про-

цесса. Для расчета качки судна входным процессом является волнение, выходным —

качка

судна. Передаточные функции определяются расчетом качки судна на

регу-

лярном

волнении или путем испытания модели судна в опытовом бассейне.

Спектральные плотности перемещений, скоростей и ускорений поперечно-

горизонтальных колебаний определяются следующими выражениями:

S..

р 5

•

I E

15)

где Sj — спектральная плотность волнения, м

с; S^ — спектральная плотность

поперечно-горизонтального перемещения, м

с; S. — спектральная плотность

скорости,

м^с"

; S.. —спектральная плотность ускорений, м

-с"

; а—частота

волнения,

с'