Благовещенский С.Н., Холодилин А.Н. Справочник по статике и динамике корабля. Динамика корабля. Том 2
Подождите немного. Документ загружается.

1,0
0,8
0,6
ОМ
по
0
П4
1
V
л
2
.
,1
N
Л
,11
т
/,
N
\\
NV
1,0
0,8
0.6
ОА
ОЛ
О
-03
1
s
2
VS
S
v
s
\
3
,11
/
\
,\
\\
\
\
v
\
Hv.
W
0.S
as
Ofi
0,2
О
^^
\ \
\
J
J
VS
N
s
\ ^
л
г%
X
к
\
ч
ч
hv.
l,t>
о?
tie
0,1
ох
\
л
II
<s
.
SxS
\S
s
ш
Ч
чЧ
1
2
3
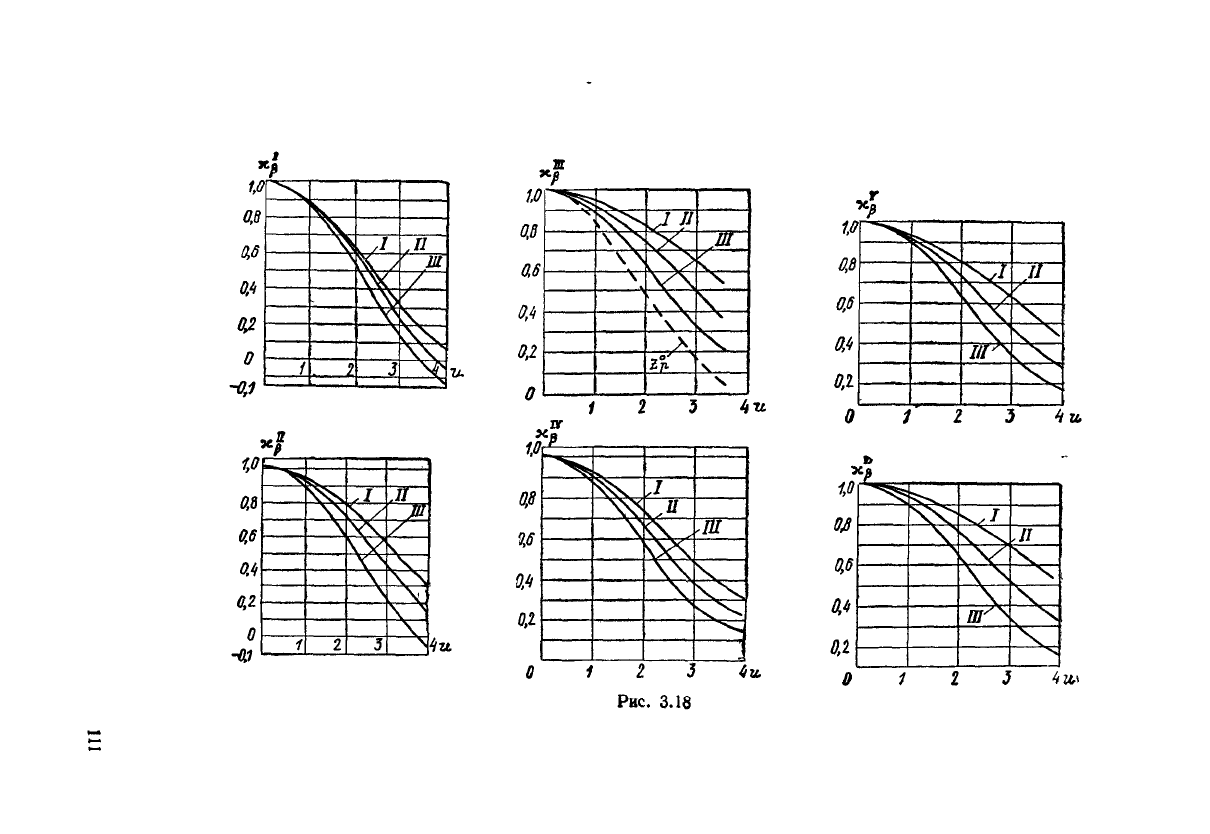
Рис.
3.18
iiv.
1.0
0,8
Ofi
1(.
0,1
S
4
\s
11
ч
ч
N
О
1
2
3
Ни,
1,0
OJS
0,6
0,1
0,1
0
w
\
s
s
V
\
v
s
.11
ч
\
ч
а
—
коэффициент полноты
ГВЛ) ft, = >l
iln
e; k —
волновое число
2яА;
3
sta
2
е
)_2х;(-|-)
4
^(3
+
5
sin
2
e)]
I
X
f t
s
(-ff)
IPs
+
-jg-toP?
(1
+"cos
a
8) —
$
6
p,
cos
2
el 11
t
?
-£*
(1
+
21 cos»
e)
+A|j
e
A (1 + 3
cos*
e)] +
T
*
S
(4
У
p
»
x+
4-
^
7 (2+9
c6s
'
8 e)
-
-
*2 {Vb -
kT
[%
•%•
+ Ь (Pi ~
2
ХРб cos
2
e) ] +
Щ{kT [^ ^L + ф
7
(р
х
+ 2р
0
cos
2
e)] -
112
где Zp—аппликата центра тяжести во второй подвижной системе
(г
р
-==
О* '«Щ§
центр тяжести расположен в плоскости ватерлинии равновесия);
z
ffl
—
погружение
центра величины г
ш
= Т — z
c
,
%
— коэффициент вертикальной полноты судна.
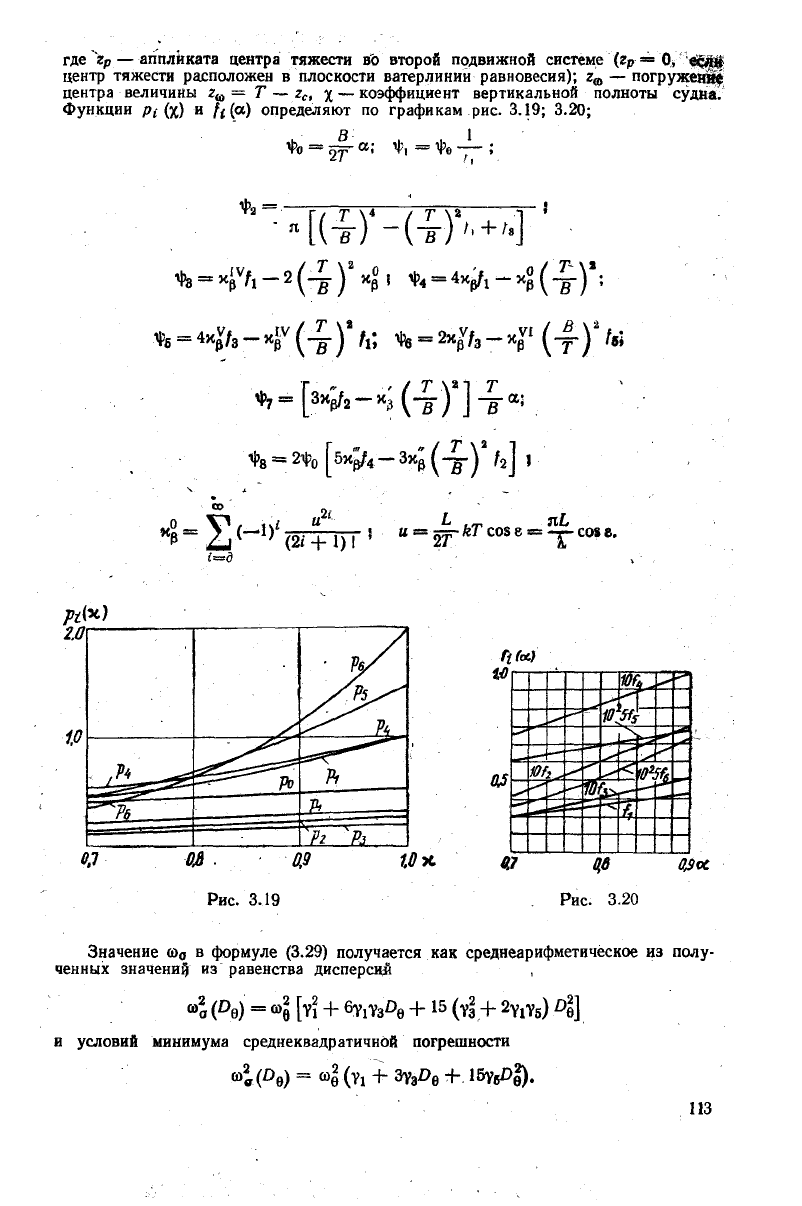
Функции
pi (x) и ft (а) определяют по графикам рис. 3.19; 3.20;
Ф
«; г|з т|> L
Г/ Г \
4
/ Г \* , I
"[(-г)
-(тт)'• +
'•]
! U еж —- kT COS 8
<
COS t.
2.0
1.0
. ;—.—•
[ft
,.
... i ' -
0.7 OA .
Рис.
3.19
iO
•л
^-
1=
1
г:
«7
0J3U.
Рис.
3.20
Значение
ш
0
в
формуле
(3.29)
получается как среднеарифметическое из полу-
ченных значений из равенства дисперсий
•4
(°в)
=
°>в
[т?
+
6
W3°e
+
15
(vi +
2
YiVs
и
условий минимума среднеквадратичной погрешности
ш
(°)
=
ш
(V
ИЗ

Тогда
"
. - . - - - I? tO Q1 \
где применена замена диаграммы остойчивости параболой 5-й степени
/
(в)
=
Yl
e
+
т
8
в
3
+
у
ъ
».
Передаточная
функция уравнения
(3.29)
определяется зависимостью
Отсюда спектральная плотность
углов
качки
..2
Переход к спектру кажущихся частот определяется формулой
ГДе
V
^ таг(
|
K
^)
a
2
получается из известной зависимости о
к
= a + feo cos e = а -{ о cos e.
Знак
перед корнем выбирается в зависимости от изменения частот при
ходе
судна под
косым
курсом.
Дисперсия
углов
качки
Так
как в правую часть расчетной формулы (3.34) входят величины/зависящие
от дисперсии DQ, практическое ее определение придется вести методом последова-
тельных приближений.
В качестве первого приближения В. В. Луговский предлагает принять пере-
даточную функцию в виде
__
у
О В \'О 0 ' 1|/ р К ' \'О Л К/ /о ое»
где
\
1^5«-0.36)1
к^
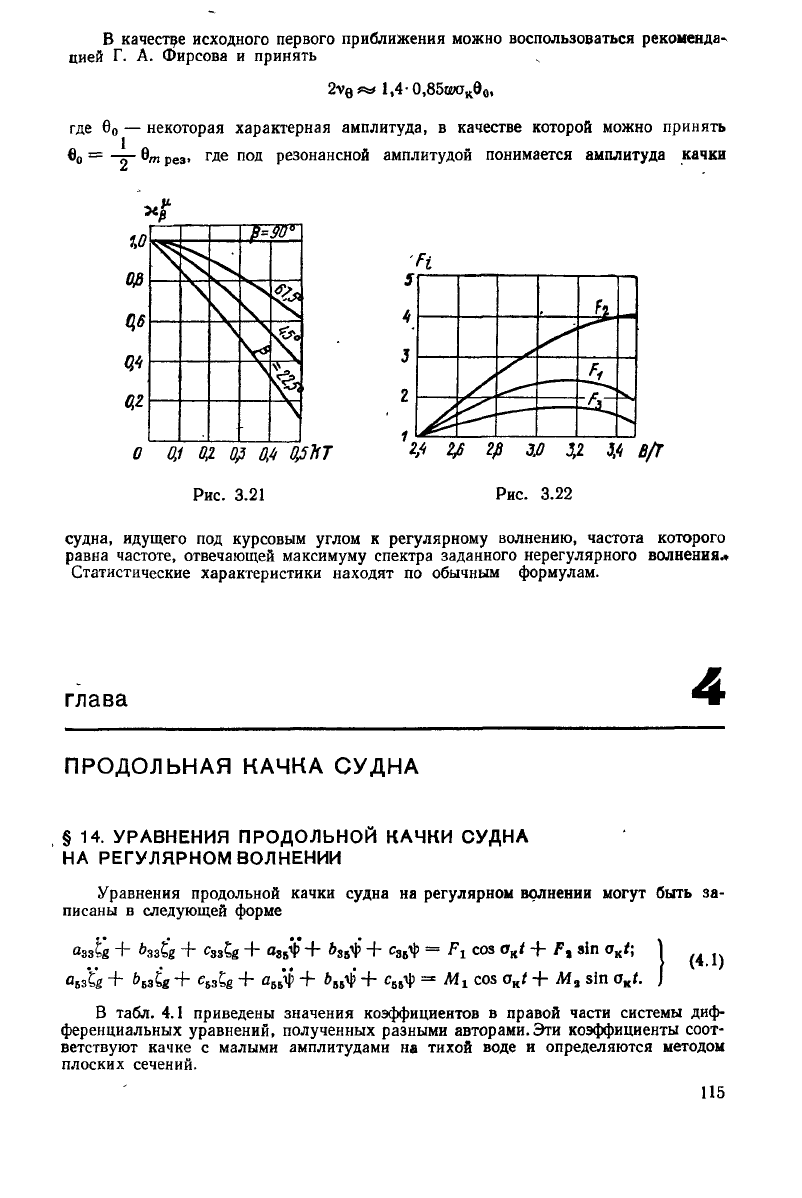
определяют по рис. 3.21; F
t
и F
2
— по риа 3.22.
В случае квадратичного -сопротивления расчет по формуле (3.35) также
следует
вести методом последовательных приближений, так как в правую часть входят вели-
чины,
зависящие от D,.
114
В качестве исходного первого приближения можно воспользоваться рекоменда-
цией
Г. А.
Фирсова
и
принять
где
8
0
—
некоторая характерная амплитуда,
в
качестве которой можно принять
fl
0
=
-£- в
т рез
, где под
резонансной амплитудой понимается амплитуда
качки
ив
о»
Ц6
\
ч
ч
S
1
\
р=$0
е
""ч
\
s
V
\
О
0,1 0,2 Op ОА
Рис.
3.21
.
•—
3
2fi
3J Д
Рис.
3.22
В/Т
судна, идущего
под
курсовым
углом
к
регулярному волнению, частота которого
равна частоте, отвечающей максимуму спектра заданного нерегулярного волнения..
Статистические характеристики находят
по
обычным формулам.
глава
ПРОДОЛЬНАЯ
КАЧКА СУДНА
§
14.
УРАВНЕНИЯ
ПРОДОЛЬНОЙ
КАЧКИ
СУДНА
НА
РЕГУЛЯРНОМ
ВОЛНЕНИИ
Уравнения продольной качки судна
на
регулярном
волнении могут быть за-
писаны
в
следующей форме
a
3
st'g
+
6зз£й
+
c
ss£g
+
a
65
ij>
=
F
x
cos a
K
t + F
t
sin a
K
t;
=
M
x
cos a
K
t -f M
а
sin a
K
/.
(4.1)
В табл.
4.1
приведены значения коэффициентов
в
правой части системы
диф-
ференциальных уравнений, полученных разными авторами. Эти коэффициенты соот-
ветствуют
качке
с
малыми амплитудами
на
тихой воде
и
определяются методом
плоских сечений.
115
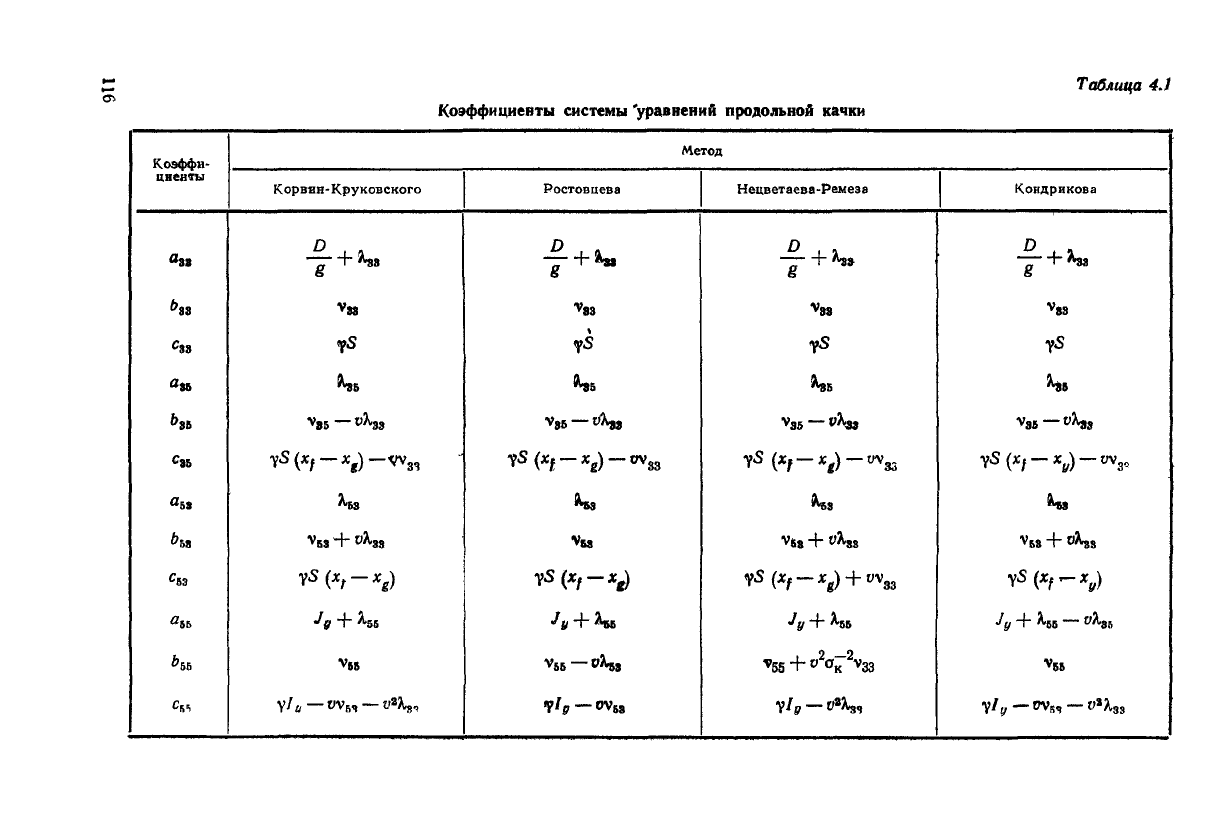
Таблица
4.1
Коэффициенты
системы 'уравнений продольной качки
Коэффи-
циенты
"si
с
88
а»
&S»
«5»
«56
Ььь
Метод
Корвян-Круковского
8
V»
Ростовцева
In
v
6B
-^s
Нецветаева-Ремеза
Vss
^
B
V
36
— O\j,
v
e8
+^
88
Кондрикова
Y
s
я*.
•^J/
4" ^55 — ^81>
v«
Y/j,
— ov
B
, —
w*>,3
S

Так,
по
методу
Кондрикова
— + |
А,
(х) dx = — -f A
M
тс.м-1-с»|
J
(ж) dx = v
83
, тс.м-
1
-с;
Css = Y |
6
(*)
dx
= YS. ТС М"
1
;
я»
=
а
5з=|
«А. (ж) djc = Яз
6
, тс-с
а
,
fr
»s
=
J *v
(*) &с
— tf J
A (x)
dx
•=
у,
в
—
»X.
gg
,
TG-OI
«as
= Y J xb (x) dx — v J v
(*) dA;
= yS (xf — x
g
) —
Wgs
то|
ft
6
,
=
J xv (x) dx + v J X (x) dx = v
6g
+ оА,
ю
,
TC-CI
C
68
— Y J xb
(x)
dx = yS (xf — x
g
), TCI
=
^ + J
A.(*) Jc
2
dx
—
У
J
A.(x)
xdx = /
B
+ i.
№
-
оЯ,
8
. тс-м-с»!
*5Б
= J
V
(*)
x
* dx = V
W
,
TC-M'C!
65 = У I
b
(x) x* dx — vb
m
= yl
y
— w
M
+
t/
2
A,
88
,
тс.M.
Здесь и
далее
обозначено х — абсцисса сечения в системе координат, связанной
с судном (начало координат в центре тяжести судна, положительное направление
оси
х в нос); А, (х) — присоединенная масса при вертикальной качке для шпангоута
единичной
длины; v (д:) — сопротивление при вертикальней качке для шпангоута
единичной
длины; Jy — момент инерции массы судна относительно центра тяжести
судна; D — водоизмещение судна; g — ускорение силы тяжести; у — удельный
вес воды; b (х) — удвоенная ордината по ватерлинии; А,з—суммарная присоеди
ненная
масса для судна при вертикальной качке; v,
3
— суммарный коэффициент
сопротивления для судна при вертикальной качке; А,
ББ
— суммарная присоединен
ная
масса (присоединенный момент инерции) при килевой качке; v
66
— суммарный
коэффициент
сопротивления при килевой качке, Я,
5
= \
3
— суммарный статиче
ский
момент присоединенной массы при взаимном влиянии килевой и вертикаль
ной
качки (при отсутствии
хода
судна); v
36
= v
6g
— суммарный коэффициент сопро
тивления от взаимного влияния килевой и вертикальной качки при отсутствии ско
рости судна, */ — абсцисса центра тяжести площади ГВЛ; Xg — абсцисса центре
тяжест»
судна, S — площадь ГВЛ судна; 1у — момент инерции площади ГВЛ,
v — скорость судна.
117

Правые части уравнений (4.1) вычисляют по следующим формулам:
ГА* -
а
о
= \ b (х) cos kx dx; b
e
= j b (x) sin kx dx;
L L
OQ •» f v (x) cos kx dx; b'
o
= v (x) sin Ax dx;
L L
OQ
«= [ А (x) cos
Ax'dx;
(.> U (x) sin Ax dx[
2.
I
a
x
= I x6 (x) cos их dx; ft
t
= • I xb, (x) sin kx dx;
L L
a{ = xv (x) cos йдс dx; 6f = I *v (x) sin Ax dx;
it
a\ = I xA (x) cos /fex dx; b\ = I xA- (x) sin kx dx.
L L
При
вычислении этих интегралов, А (х) и v (x), входящие в правые части
уравнений (4.1),
следует
рассматривать как функции истинной частоты волны а,
в
то время как величины A
8S
, v
38
, A
66
, v
65
, A
S5
, v
S6
, А
б8
, v
68
, входящие в левые части
системы уравнений продольной качки, должны рассматриваться как функции ка-
жущейся частоты а
к
.
Приведенный
радиус волны г
т
= у.
г
г
а}
, где х
2
— поправочный коэффициент
к
возмущающей силе по осадке при вертикальной качке.
Частное решение системы дифференциальных уравнений продольной качки
(4.1), определяющее вынужденные колебания судна,
£« •— £l
cos
°к' — £г
sirt а
к* = lm (Oj — h)> I IA m
г|з = i|5j cos a
K
t — tf>
8
sin a
K
t = ty
m
(a
K
t — бф), J
где Zm
и
'Фт — амплитуда вертикальной и килевой качки, а 6^ и б^, — соответствую-
щие фазовые
углы.
Очевидно, ' .
,
т
— у *>i I *2> Т/л
Согласно вычислениям Ю. В. Ремеза, коэффициенты равны
bd _ ad — be
^' a
2
+ ft
2
'
Тг
a
2
+
U8
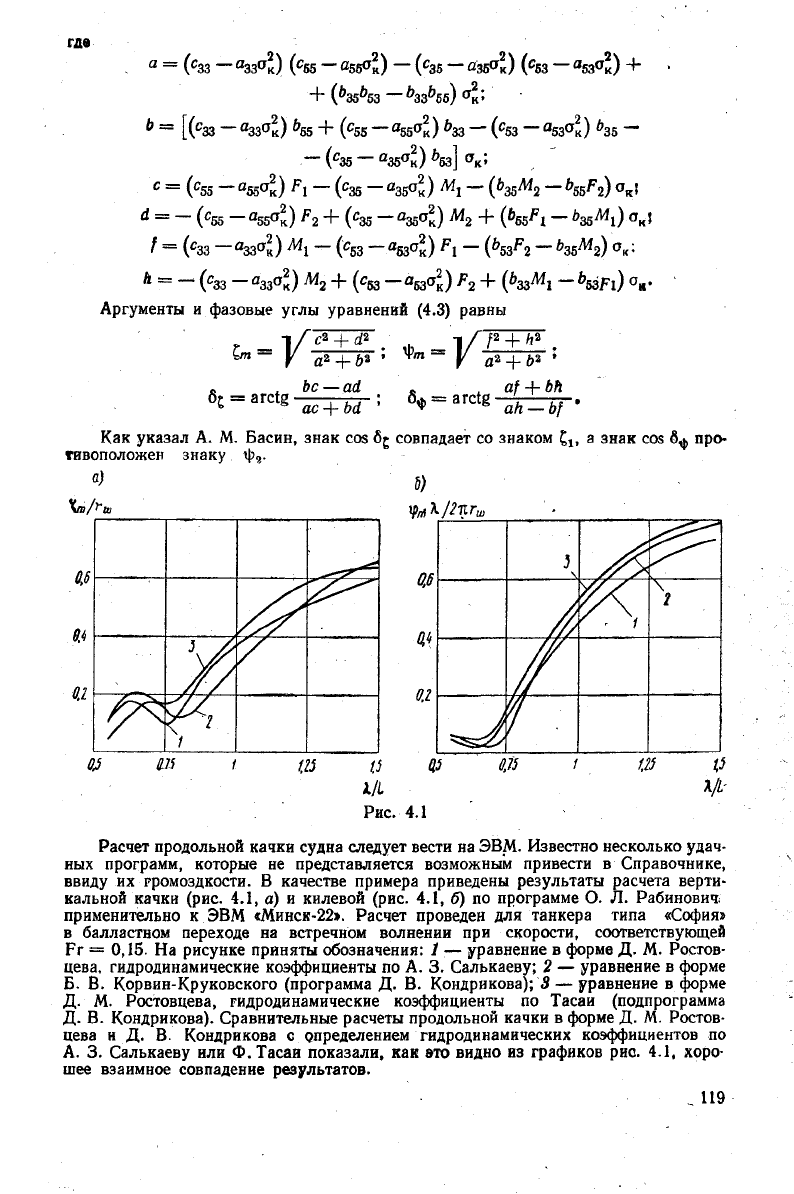
где
,
а
— (
С
33 —
а
33
а
к)
(
С
65 —
«Бб
0
»)
— (
С
35 —
Ь
= [(
С
33 -
а
ЗЗ°к)
6
55 + (
С
55 —
°55°к)
6
33 — (
С
53 ~
— (
с
з5 -
с
з5
а
к) *бз] <*
к
;
с = (c
5S
-
Вя
о»)
Fi - (egg -
а
Ъ5
о1)
М, - (^М,
d
= - (
С
55 -
а
55<1к) ^2 + (
С
35
-°35Ок)
^2 + С'бЗ^
^ = (
С
33
—°ЗЗОк)
^1 - (С
5
3
-
а
53°к)
f
l - (*53^2
ft
=
- (
С
33 - «ЗЗ^к) ^2 + («63 -
а
53<4) ^2 + (^33^
Аргументы
и фазовые
углы
уравнений (4.3) равны
-
b
55
F
2
)
а
к!
~
*36^l)
O
K
*35
М
2)
°к-
1
~
b
53Fl)
°
B
; = arctg
be — (
arctg
ac + bd '
-»--"•«
ah
_
bf
•
Как
указал А. М. Басин, знак cos 6j совпадает со знаком £
х
, а знак cos в^ про-
тивоположен знаку ф,.
а
)
' Л) •
US
0.1
У/
у
0.6
/
7
W
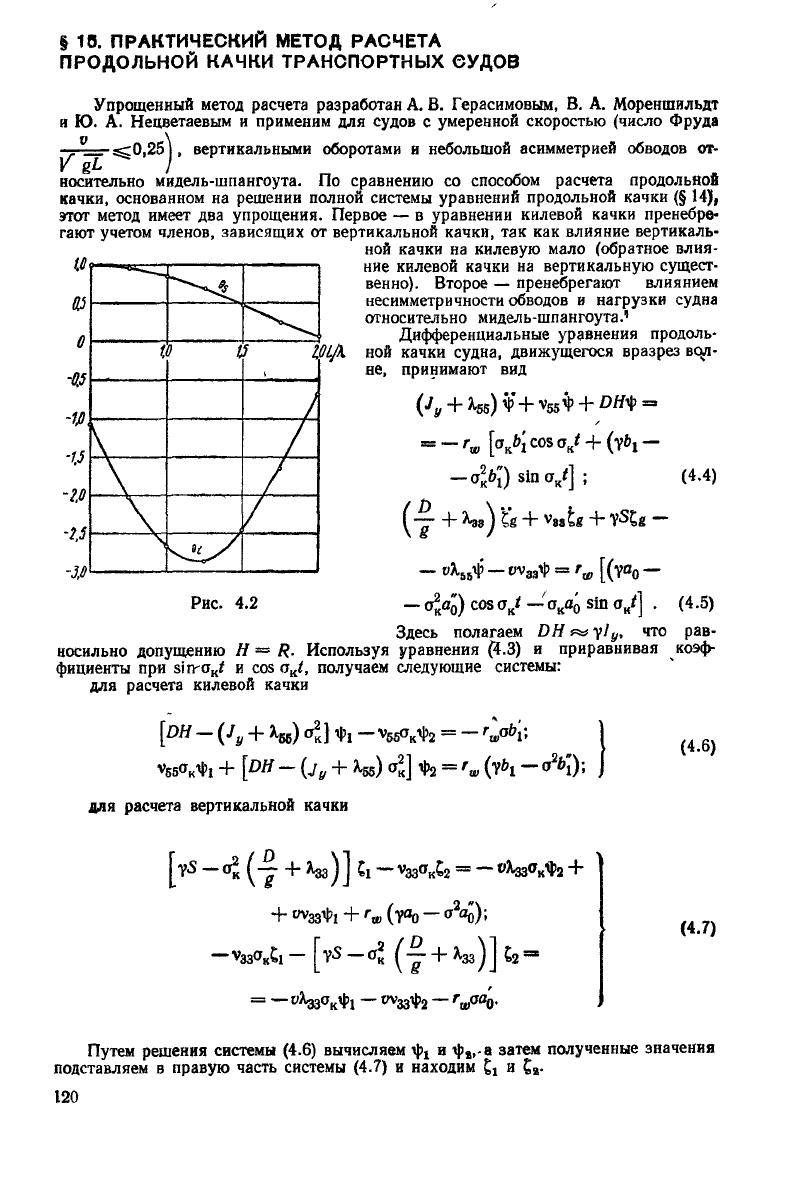
Рис.
4.1
Расчет продольной качки судна
следует
вести на ЭВМ. Известно несколько
удач-
ных программ, которые не представляется возможным привести в Справочнике,
ввиду их громоздкости. В качестве примера приведены результаты расчета верти-
кальной
качки (рис. 4.1, а) и килевой (рис. 4.1, б) по программе О. Л. Рабинович;
применительно к ЭВМ «Минск-22». Расчет проведен для танкера типа «София»
в
балластном переходе на встречном волнении при скорости, соответствующей
Fr
= 0,15. На рисунке приняты обозначения: 1 — уравнение в форме Д. М. Ростов-
цева, гидродинамические коэффициенты по А. 3. Салькаеву; 2 — уравнение в форме
Б.
В. Корвин-Круковского (программа Д. В. Кондрикова); 3 — уравнение в форме
Д. М. Ростовцева, гидродинамические коэффициенты по Тасаи (подпрограмма
Д. В. Кондрикова). Сравнительные расчеты продольной качки в форме Д. М. Ростов-
цева и Д. В. Кондрикова с определением гидродинамических коэффициентов по
А. 3. Салькаеву или Ф. Тасаи показали, как это видно из графиков рис. 4.1, хоро-
шее взаимное совпадение результатов.
_ 119
§
18. ПРАКТИЧЕСКИЙ
МЕТОД
РАСЧЕТА
ПРОДОЛЬНОЙ
КАЧКИ ТРАНСПОРТНЫХ СУДОВ
Упрощенный метод расчета разработан А. В. Герасимовым, В. А. Мореншильдт
и
Ю. А. Нецветаевым и применим для
судов
с умеренной скоростью (число Фруда
;grO,25), вертикальными оборотами и небольшой асимметрией обводов от-
носительно мидель-шпангоута. По сравнению со способом расчета продольное
качки,
основанном на решении полной системы уравнений продольной качки (§ 14),
этот метод имеет два упрощения. Первое — в уравнении килевой качки пренебре-
гают
учетом
членов, зависящих от вертикальной качки, так как влияние вертикаль-
ной
качки на килевую мало (обратное влия-
10 ние килевой качки на вертикальную сущест-
венно).
Второе — пренебрегают влиянием
gjj\ j »|^. 1 несимметричности обводов и нагрузки судна
относительно мидель-шпангоута.'
_.. , Дифференциальные уравнения продоль-
1,0 0
IOLJ\
ной качки судна, движущегося вразрез
BO^I-
не,
принимают вид
-W
-У
-2,0
'2,5
-o
2
K
bl)
sin o
K
t];
(4.4)
(у
Рис.
4.2
r
w
[(ya
0
—
- o>o) cos a
K
t —a
K
a
0
sin aj] .
(4.5)
рав-
ф
Здесь полагаем DH *=» yl
y
, что р
носильно
допущению Н — R. Используя уравнения f4.3) и приравнивая
коэф-
фициенты
при
s\n-a
K
t
и cos a
K
t, получаем следующие системы:
для расчета килевой качки
[Ш
- (J
y
+
ЧИ"Л
+ [
DH
~ Оу +
для расчета вертикальной качки
(4.6)
Ci ~
— а\);
- [y
S
-°к (у
(4.7)
Путем решения системы (4.6) вычисляем ^ и i|)
s
,-a затем полученные значения
подставляем в правую часть системы (4.7) и находим £
х
и £
s
.
120
