Благовещенский С.Н., Холодилин А.Н. Справочник по статике и динамике корабля. Динамика корабля. Том 2

Подождите немного. Документ загружается.

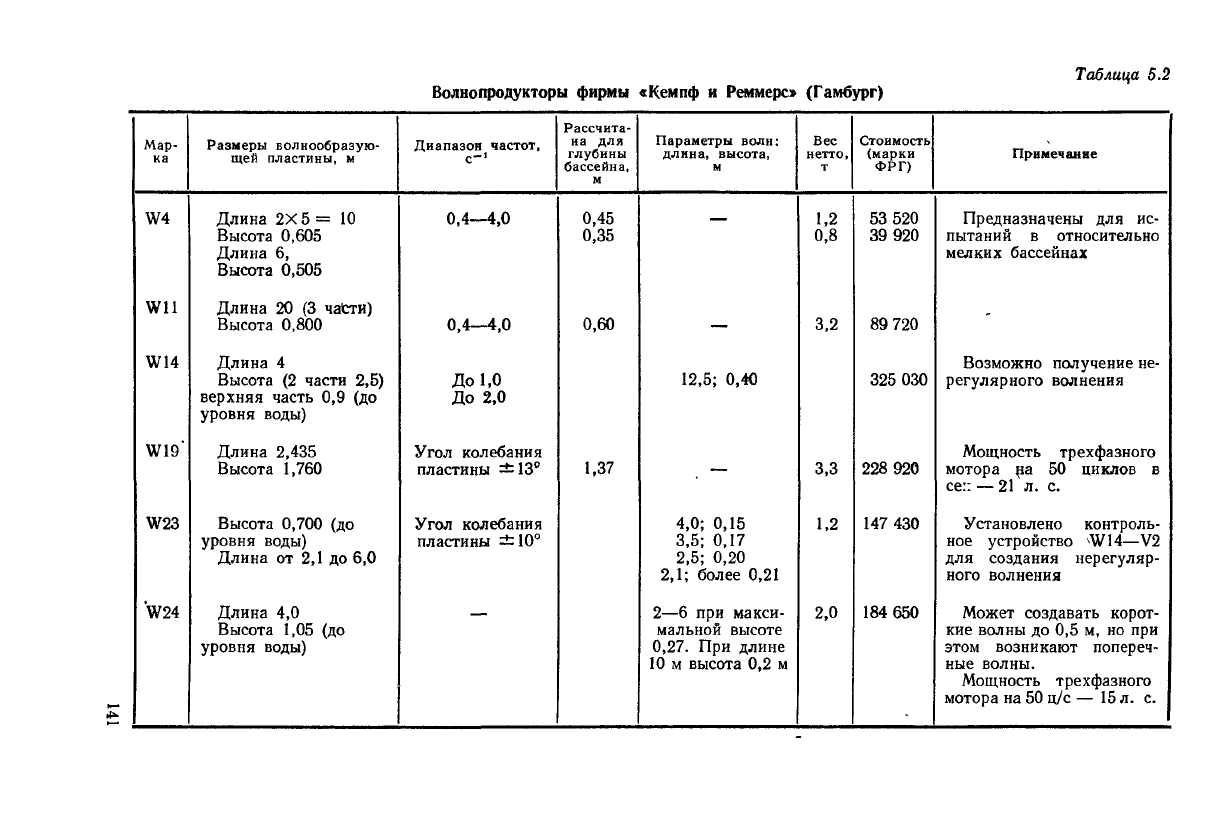
Волнопродукторы

фирмы

«Кемпф и Реммерс» (Гамбург)

Таблица

5.2

Мар-

ка

W11

W14

W19'

W23

W24

Размеры волнообразую-

щей пластины,

Длина

2X5 = 10

Высота

0,605

Длина

Высота

0,505

Длина

20 (3

части)

Высота

0,800

Длина

Высота

части

2,5)

верхняя часть

0,9 (до

уровня воды)

Длина

2,435

Высота

1,760

Высота

0,700 (до

уровня воды)

Длина

от 2,1 до 6,0

Длина

4,0

Высота

1,05 (до

уровня воды)

Диапазон частот,

с""'

0,4—4,0

До

1,0

До

2,0

Угол

колебания

пластины

±13°

Угол

колебания

пластины

±10°

Рассчита-

на

для

глубины

бассейна,

0,45

0,35

0,60

1,37

Параметры волн:

длина, высота,

—

12,5;

0,40

—

4,0;

0,15

3,5;

0,17

2,5;

0,20

2,1;

более

0,21

2—6 при

макси-

мальной высоте

0,27.

При

длине

10 м

высота

0,2 м

Вес

нетто,

1,2

0,8

3,2

3,3

1,2

2,0

Стоимость

(марки

ФРГ)

520

920

720

325

030

228

920

147

430

184

650

Примечание

Предназначены

для ис-

пытаний

относительно

мелких бассейнах

Возможно получение

не-

регулярного волнения

Мощность трехфазного

мотора

на 50

циклов

се::

— 21 л. с.

Установлено контроль-

ное

устройство

W14—V2

для создания нерегуляр-

ного волнения

Может создавать корот-

кие волны

до 0,5 м, но при

этом возникают попереч-

ные волны.

Мощность трехфазного

мотора

на 50 ц/с — 15 л. с.

влияние

поверхностного натяжения (критерий подобия Вебера)

при

определении

коэффициентов

демпфирования качки. Поэтому

следует

избегать малых

по

масштабу

абсолютным размерам моделей. Числа Рейнольдса

Вебера определяются зави-

симостями

где

V —

кинематический коэффициент вязкости;

р —

массовая плотность воды;

°п

н —

коэффициент поверхностного натяжения.

При

температуре воды

15° G

.н=72,5 дин/с

дина=

1,0197 мг); v= 1,15-10"» м

/с; р= 102

кг-с

/м«

(для пресной воды).

При

соблюдении критерия подобия

(5.1)

соотношение основных характеристив

модели

натуры- выражается следующими данными:

Величины Отношение

Линейные размеры, давление

. . м •

Углы, линейные ускорения

... 1

Линейные скорости, периоды

ко-

лебаний

1/2

Угловые скорости м""

Угловые ускорения

V м""

Площади

м*

Объемы, массы, силы

Статические моменты объемов,

массС

сил;

работа; энергия

. . м

Моменты инерции, объемов, масс

Количество движения, импульсы

сил,

мощность

Момент количества движения

. .

4>5

При

обработке результатов испытаний

и, в

частности,

при

построении ампли-

тудно-частотных графиков

—

передаточных функций, можно применять обобщен-

ный

критерий подобия, предложенный

А. Н.

Холодилиным

в 1955 г., a VUg-

Такой

параметр удобен

и при

расчете качки

на

нерегулярном волнении,

так как

выражает

коэффициент

динамичности

функции частоты. Подобное предложение согласуется

рекомендациями

9-й

Международной конференции опытовых бассейнов (Париж,

1960)

не

использовать отношение периодов

при

графическом представлении экспе-

риментального материала, ввиду трудности определения периода собственных

колебаний

на

волнении.

Двенадцатая Международная конференция опытовых бассейнов

(Рим, 1969)

обсудила

одобрила «Стандарт

1969 г. для

проведения испытаний мореходных

ка-

честв

судов

при

встречном

попутном волнении». Стандарт содержит

три

раздела:

модель, опыт, представление результатов.

Следует

придерживаться следующих

рекомендаций Стандарта.

Если неизвестны радиусы инерции,

их

следует

принимать: продольный

0.25L,

поперечный

0,45, где L и В —

длина

ширина модели соответственно.

При

замере изгибающих моментов

на

волнении

следует

обеспечить подобие

распределения нагрузки

и по

длине,

И по

вертикали.

Если

для

судна неизвестна аппликата центра тяжести,

следует

на

модели

при-

нимать

ее

равной осадке

на

тихой воде.

Собственный период бортовых колебаний модели

следует

определять

по

кривой

затухающих колебаний, начиная

амплитуды

5".

Модель должна иметь верхнюю

палубу,

полубак, фальшборт,

и, по

возможности,

все выступающие части.

Здесь <аа

—

масштаб модели.

142

Следует

избегать условий испытания моделей

бассейне, когда

влияние стенок бассейна.

Направляющая система должна иметь минимальное влияние

на

продольные

килевые

вертикальные колебания модели.

Следует

фиксировать килевую

вертикальную качку, вертикальные ускорения

(в

точках

0,1 и 0,9

длины модели

между

перпендикулярами), движение форштевня

относительно поверхности воды, фазовые

углы

относительно волны, высоту волны.

При

самоходных испытаниях

следует

фиксировать параметры двигателя

винта.

При

испытаниях

на

регулярном волнении стандартных

судов

на

каждой

ско-

рости должно быть проведено

не

менее

опытов, охватывающих длины волн

от

0,5L

до 2.0L. Для

быстроходных

судов

диапазон длин волн должен быть расширен

тем,

чтобы охватить район резонанса.

РЦ.

I I I I I I I I I I I t IJ I I

Средние значения амплитуд и периодов качки необходимо определять по записи

не

менее 10 циклов.

При

испытании на нерегулярном волнении для повышения точности

следует

получать не менее 200 циклов для определения спектров. Для определения средних

значений

параметров движения модели и волн можно ограничиться

80—100

циклами

колебаний.

Результаты испытания должны быть нанесены на графики в функции отношения

длины волны к длине судна, по оси ординат должны откладываться относительные

амплитуды

При

испытаниях на нерегулярном волнении передаточную функцию необходима

определить в функции кажущейся частоты.

Высоту

волны рекомендуется определять как значительную (среднее значение

из

одной трети наибольших). При этом она

будет

связана с дисперсией соотношением

1/3

= 4,0 \

Dr, где D. — дисперсия процесса. В отечественной практике оценка

волнения

производится по высоте волны 3%-ной обеспеченности, Лзо

/о

l,32ftj^

При

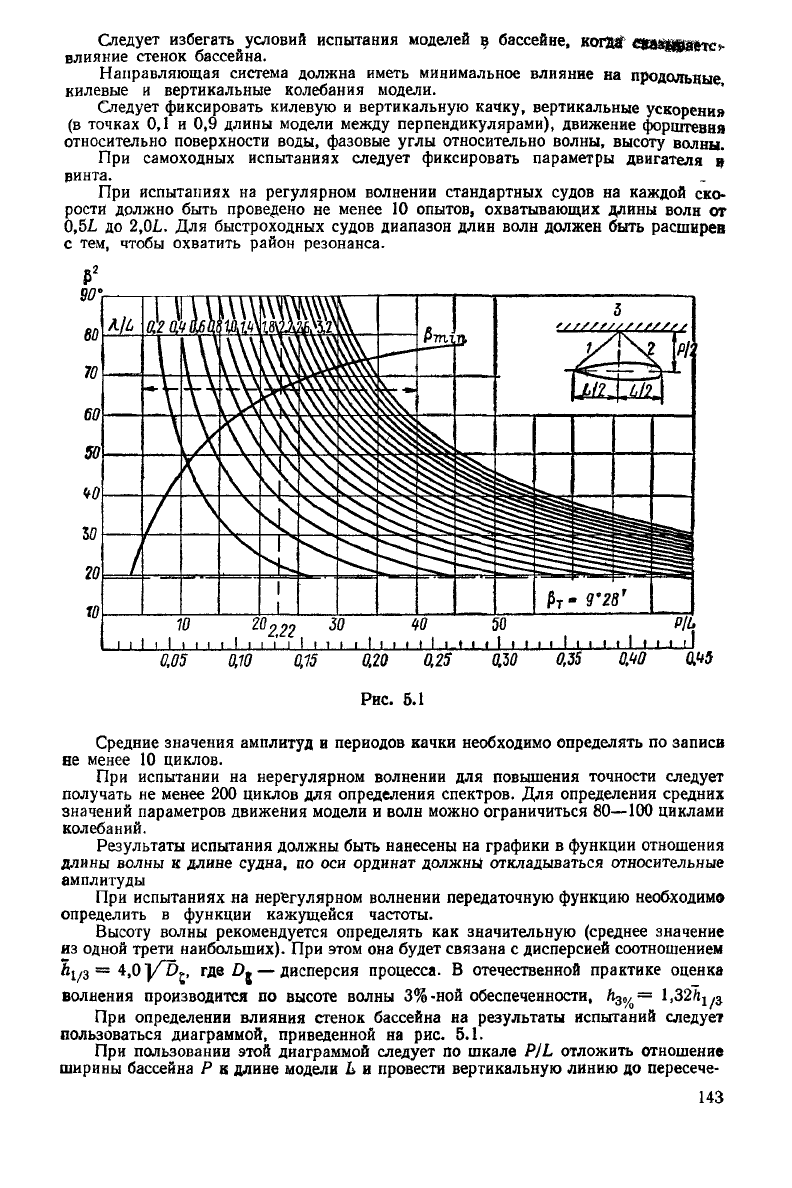
определении влияния стенок бассейна на результаты испытаний

следует

пользоваться диаграммой, приведенной на рис. 5.1.

При

пользовании этой диаграммой

следует

по шкале P/L отложить отношение

ширины

бассейна Р к длине модели L и провести вертикальную линию до пересече-

143

ния

с кривой P/L, соответствующей минимальному

углу

р, при котором имеет место

интерференция

для заданного PIL. Через данную точку

следует

провести горизон-

тальную прямую, параллельную оси абсцисс. Тогда все точки, лежащие на этой

прямой,

укажут

на наличие влияния стенок бассейна. Условия испытаний должны

соответствовать таким комбинациям чисел Фруда и отношениям длины волны к длине

модели X/L, которые находятся под горизонтальной прямой. В качестве примера,

на

диаграмме приведено построение для PIL = 2,22. Тогда при Fr = 0,10 влияние

стенок

бассейна начинает сказываться при

%IL

= 0,9, а при Fr = 0,20 при X/L ^ 3,6

и.

т. Д. .

На

рис. 5.1 обозначено: 1 — волновой фронт; 2 — отраженный волновой фронт;

•8

— стенка бассейна.

§ 20. МЕТОДИКА

ПРОВЕДЕНИЯ

ИСПЫТАНИЙ

КАЧКИ

МОДЕЛЕЙ СУДОВ

Для удовлетворения динамического подобия модель (геометрически подобная

натуре) подвергается статической и динамической тарировке. Первое определяет

подобие по расположению центра тяжести модели и натуры, второе — подобие

моментов инерции массы. Наибольшее распростране-

ние

получил способ С. Н. Благовещенского.

Модель подвешивают на ножах и раскачивают.

Замеряют период колебания модели при первом поло-

жении

груза

— т

и при втором т

(рис. 5.2). Рас-

стояние

центра тяжести модели от оси качания при

первом положении

груза

определяется зависимостью

Р1

где Р — вес перемещаемых грузов вместе со штангой,

кгс;

/ — расстояние переноса

груза

по высоте м; г —

расстояние оси штанги с грузами в первом положении

Рис.

5.2

от

оси колебания, м; D — водоизмещение, кгс; g —

ускорение силы тяжести, мс

Момент инерции массы модели относительно оси, проходящей через центр ее

тяжести, при первом положении грузов

После

перемещения

груза

Р1

Зная

момент инерции массы модели и положение ее центра тяжести по высоте,

можно подобрать необходимые значения. Динамическая тарировка модели должна

выполняться

с большой тщательностью, так как все неточности, допущенные при

тарировке, явятся источниками систематической погрешности при опыте.

Метод свободных

затухающих

колебаний. Этот метод применим только при

моделировании бортовой качки. Обработка записи бортовых

затухающих

колебаний

модели (рис. 5.3) позволяет определить период собственных бортовых колебаний,

коэффициент

демпфирования качки и присоединенный момент инерции

144

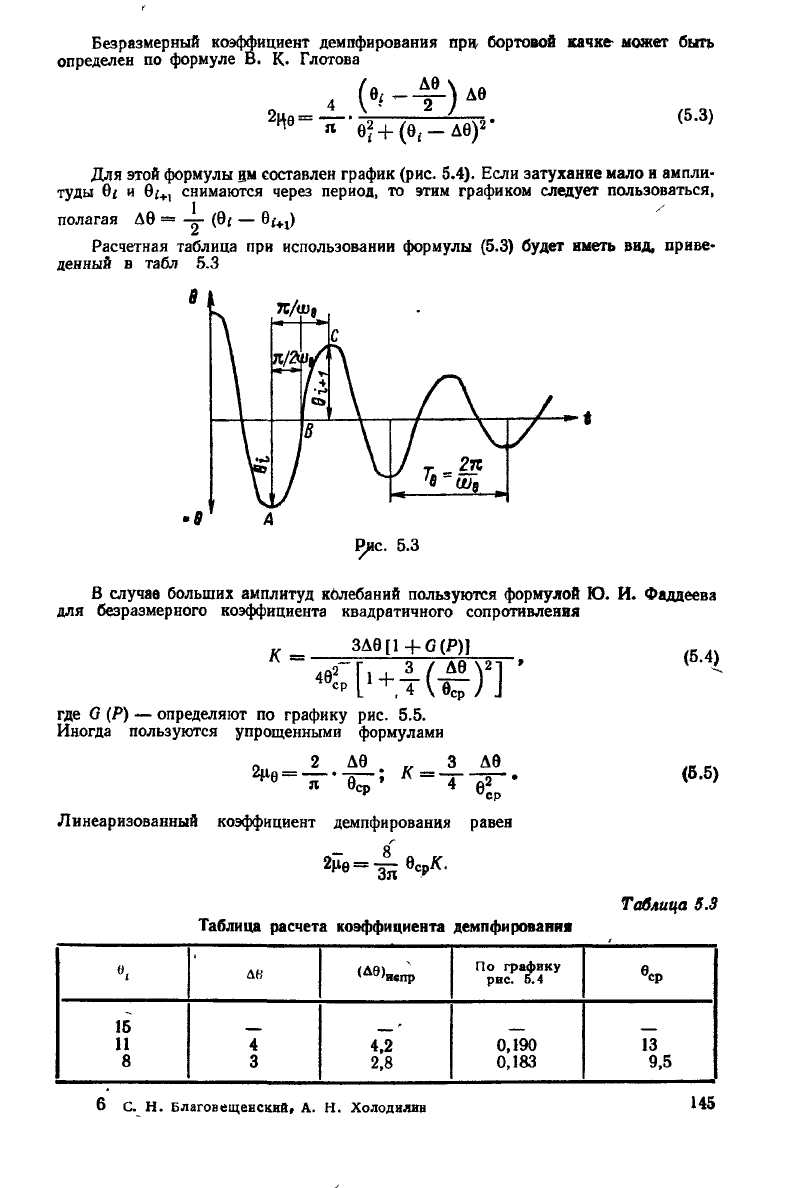
Безразмерный

коэффициент демпфирования

при

бортовой качке может быть

определен

по

формуле

В. К.

Глотова

-'-—

)

Д9

(5.3)

Для этой формулы

им

составлен график (рис.

5.4).

Если затухание мало

ампли-

туды

Qt и

Qc+i

снимаются через период,

то

этим графиком

следует

пользоваться,

полагая

Аб = -д- (6* — в^

)

Расчетная таблица

при

использовании формулы

(5.3) будет

иметь

вид,

приве-

денный

табл

5.3

с. 5.3

случав

больших амплитуд кблебаний пользуются формулой

Ю. И.

Фаддеева

для безразмерного коэффициента квадратичного сопротивления

ЗАв[1

Ав\2

где

G (Р) —

определяют

по

графику

рис. 5.5.

Иногда пользуются упрощенными формулами

2ц = J-.—- к

А8

Линеаризованный

коэффициент демпфирования равен

(5.4)

(6.5)

Таблица расчета коэффициента демпфирования

С. Н. Благовещенский, А. Н. Холодилин

Таблица

5.3

в,

4,2

2,8

По

графику

рве. 5.4

0,190

0,183

9,5

145

Таблица

5.4

Амплитуда

качки

0,00—0,10

0,10—0,20

0,20—0,30

0,30—0,40

0,40—0,50

0,50—0,60

0,60—0,70

0,70—0,80

0,80—0,90

0,90—1,00

1,00—1,10

1.п

II.

III.

Т*

—4

—3

—z

—1

0,00—0

—5

с»

0,10—0

—4

0,20—0

—3

0,30—0

—2

0,40—0,

-а

со

0,50—0

—

—8

—12

~0~

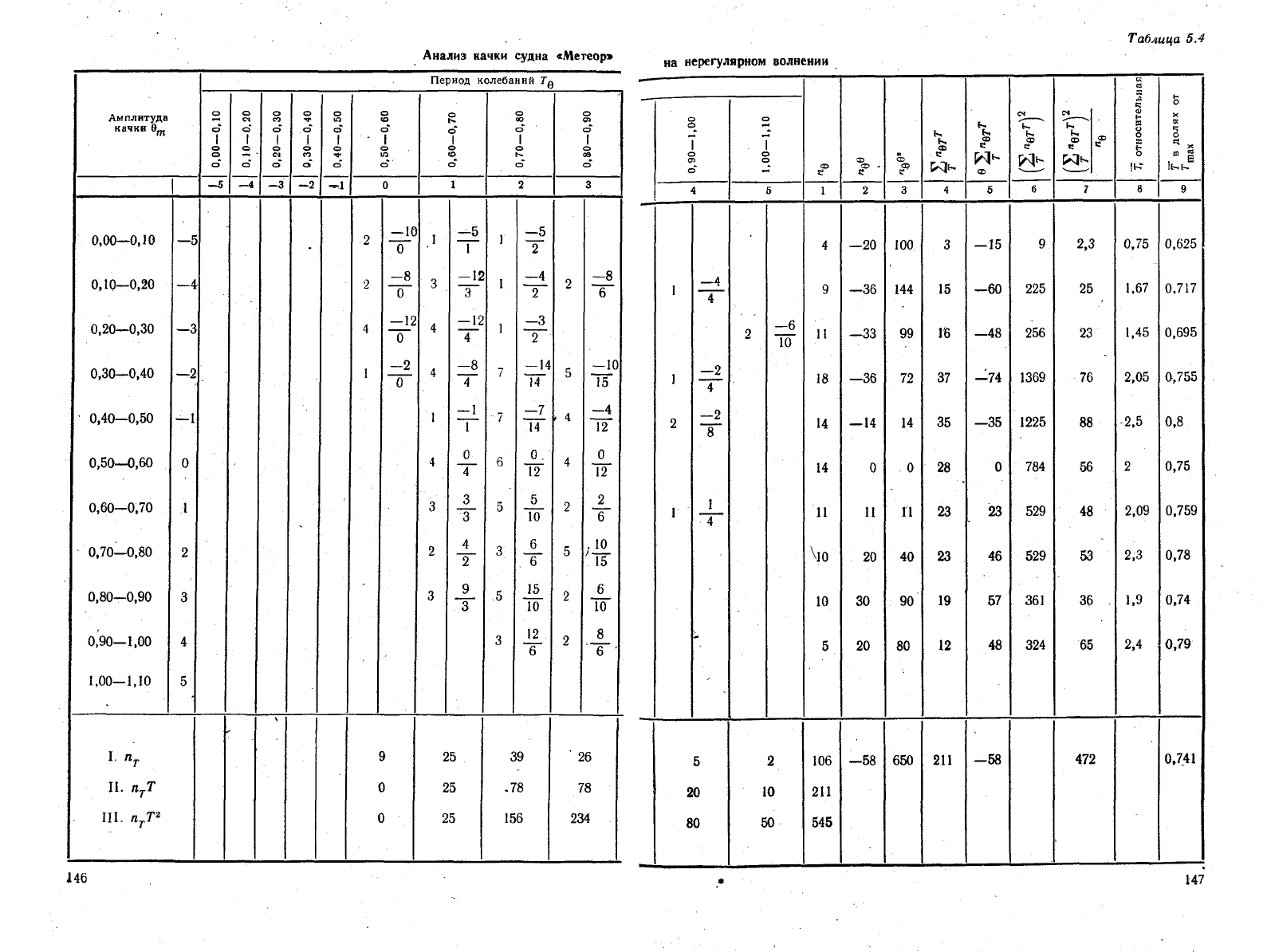
Анализ

качки

судна

Период колебаний

(

0,60—0,

—5

—

—8

—

со

ОЭ

0,70—0

-7

—5

—4

—3

—14

—7

со

.78

156

«Метеор»

СП

0,80—0

•

—8

—10

—4

'15

6 '

234

на

нерегулярном

—4

—2

—6

\|0

106

211

545

—20

—36

—33

—36

—14

—58

100

144

650

(-,

1'6

211

к,

—15

—60

—48

—74

—35

-58

С*

225

256

1369

1225

784

529

361

324

С*

2,3

472

Т,

относительная

0,75

1,67

1,45

2,05

2,5

2,09

2,3

1,9

2,4

долях

от

max

0,625

0,717

0,695

0,755

0,8

0,75

0,759

0,78

0,74

0,79

0,741

146

147

Амплитуда

IV.

2>er

Г2»,

С2

вг

VII

V* '

VIII.

в отно-

сительная

IX. 8 в

долях

от

шах

0-0

•-•

-4

отн

г/в

г/

/г

-3.

СО

—2

"г

Д'

—32

1024

114

—3,56

0,194

долях

Период

—22.

—22

484

19,3

—0,88

0,462

№

о1Я

+ 0,55

Коэффициент корреляции

2>ет-ге

(2VW2

г 8 \т . }\.р

Коэффициенты регрессии

ег

(|>е

-($у)

по

« 0.205 =

w°-

20S

колебаний

Та

0,641

0,128

0,563

0—0,

0,616

0,154

0,564

0 205;

Т..

0.464;

0,098.

Продолжение

табл. 5.4

148

—7

—28

9,8

-м..

0,41

—6

-30

—3

0,25

—58

-58

162,4

-8,56

0,40

OTH

""'

Корреляционные отношения

Чг/6

•

Г n^

r._(s^)

0,460;

0,643.

149

Приближенное

значение к

можно получить

= J

— J

где J

— момент инерции массы модели;

(£)'

»•

— период собственных бортовых колебаний на воде, с; D — водоизмещение, кгс;

h — поперечная метацентрическая высота, м.

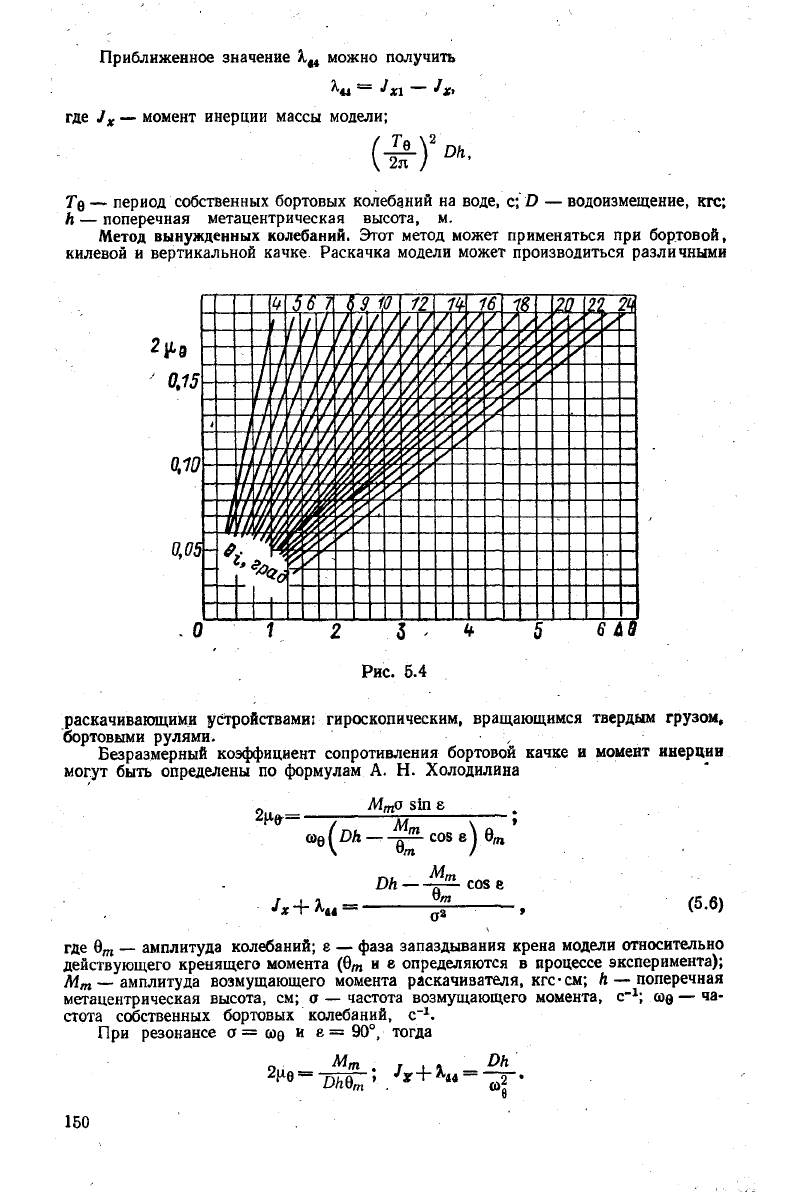
Метод вынужденных колебаний. Этот метод может применяться при бортовой,

килевой и вертикальной качке Раскачка модели может производиться различными

Рис.

6.4

раскачивающими устройствами; гироскопическим, вращающимся твердым грузом,

бортовыми рулями. - • ,

Безразмерный

коэффициент сопротивления бортовой качке и момент инерции

могут

быть определены по формулам А. Н. Холодилина

о.. _

osine

_/.

Dh ——

cos

(5.6)

где %

— амплитуда колебаний; е — фаза запаздывания крена модели относительно

действующего кренящего момента (6

и е определяются в процессе эксперимента);

— амплитуда возмущающего момента раскачивателя, кгс-см; h — поперечная

метацентрическая высота, см; а — частота возмущающего момента, с"

; сое —

ча

стота собственных бортовых колебаний, с"

При

резонансе а = сое

и в

= 90°,

тогда

М„

150

Метод испытания на регулярном волнении. Этот метод применим при любом

виде качки. При изучении качки модели на волнении можно построить амплитудно-

частотный график, который используется, в частности, как передаточная функция

при

расчете качки на нерегулярном волнении. Построение амплитудного графика

является простым, но трудоемким экспериментом. Модель многократно испытывают

при

различных параметрах волнения. Частоты волнения

следует

изменять с таким

расчетом, чтобы охватить во время испытания зону резонансной качки модели.

Поскольку каждый отдельный опыт обычно дублируется, приходится проводить

от 30 до 50 испытаний для получения достаточно надежной кривой амплитудно-

частотного графика. Это наиболее надежный, хотя и трудоемкий, способ опреде-

ления

передаточной функции.

Время проведения испытаний для получения передаточных функций качки

может быть значительно снижено, если применить метод определения передаточ-

ных функций качки путем испытания моделей

судов

на кратковременном неус-

тановившемся волнении по

методу

Афре-

мова, Бородая и Вознесенского.

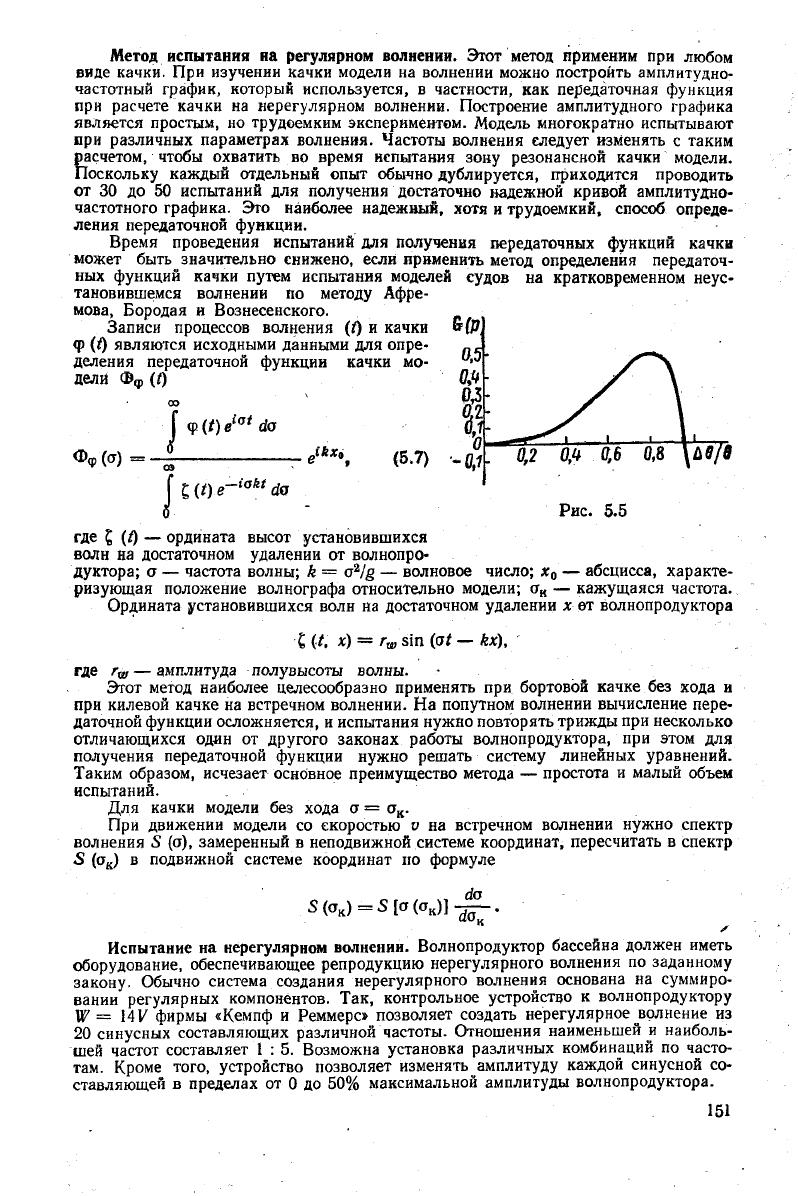
Записи

процессов волнения (f) и качки

(<) являются исходными данными для опре-

деления передаточной функции качки мо-

дели Ф

(/)

Фф(а)

СО

<p(t)e

>at

(5.7)

Рис.

5.5

где £ (f) — ордината высот установившихся

волн на достаточном удалении от волнопро-

дуктора; а — частота волны; k = aVg — волновое число; х

— абсцисса, характе-

ризующая положение волнографа относительно модели; а

— кажущаяся частота.

Ордината установившихся волн на достаточном удалении х ет волнопродуктора

•£ (t, х) = т

sin (at — kx),

где r

— амплитуда полувысоты волны.

Этот метод наиболее целесообразно применять при бортовой качке без

хода

при

килевой качке на встречном волнении. На попутном волнении вычисление пере-

даточной функции осложняется, и испытания нужно повторять трижды при несколько

отличающихся один от

другого

законах работы волнопродуктора, при этом для

получения передаточной функции нужно решать систему линейных уравнений.

Таким

образом, исчезает основное преимущество метода — простота и малый объем

испытании.

Для качки модели без

хода

а — а

При

движении модели со скоростью v на встречном волнении нужно спектр

волнения

S (а), замеренный в неподвижной системе координат, пересчитать в спектр

S (а

) в подвижной системе координат по формуле

Испытание

на нерегулярном волнении. Волнопродуктор бассейна должен иметь

оборудование, обеспечивающее репродукцию нерегулярного волнения по заданному

закону. Обычно система создания нерегулярного волнения основана на суммиро-

вании

регулярных компонентов. Так, контрольное устройство к волнопродуктору

= 14 V фирмы «Кемпф и Реммерс» позволяет создать нерегулярное волнение из

20 синусных составляющих различной частоты. Отношения наименьшей и наиболь-

шей

частот составляет 1 : 5. Возможна установка различных комбинаций по часто-

там. Кроме того, устройство позволяет изменять амплитуду каждой синусной со-

ставляющей в пределах от 0 до 50% максимальной амплитуды волнопродуктора.

151

По

результатам обработки записей испытания составляют корреляционную

таблицу связи амплитуд и периодов колебаний модели судна. Для этого используются

яри

ручной обработке записи шаблоном с градуировкой 0,1 максимального значе-

ния,

с помощью которого (Определяют число замеренных величин. Шаблон градуи-

руют

от 0 до 1,1 максимальной величины. Запись в таблицу

ведут

следующим обра-

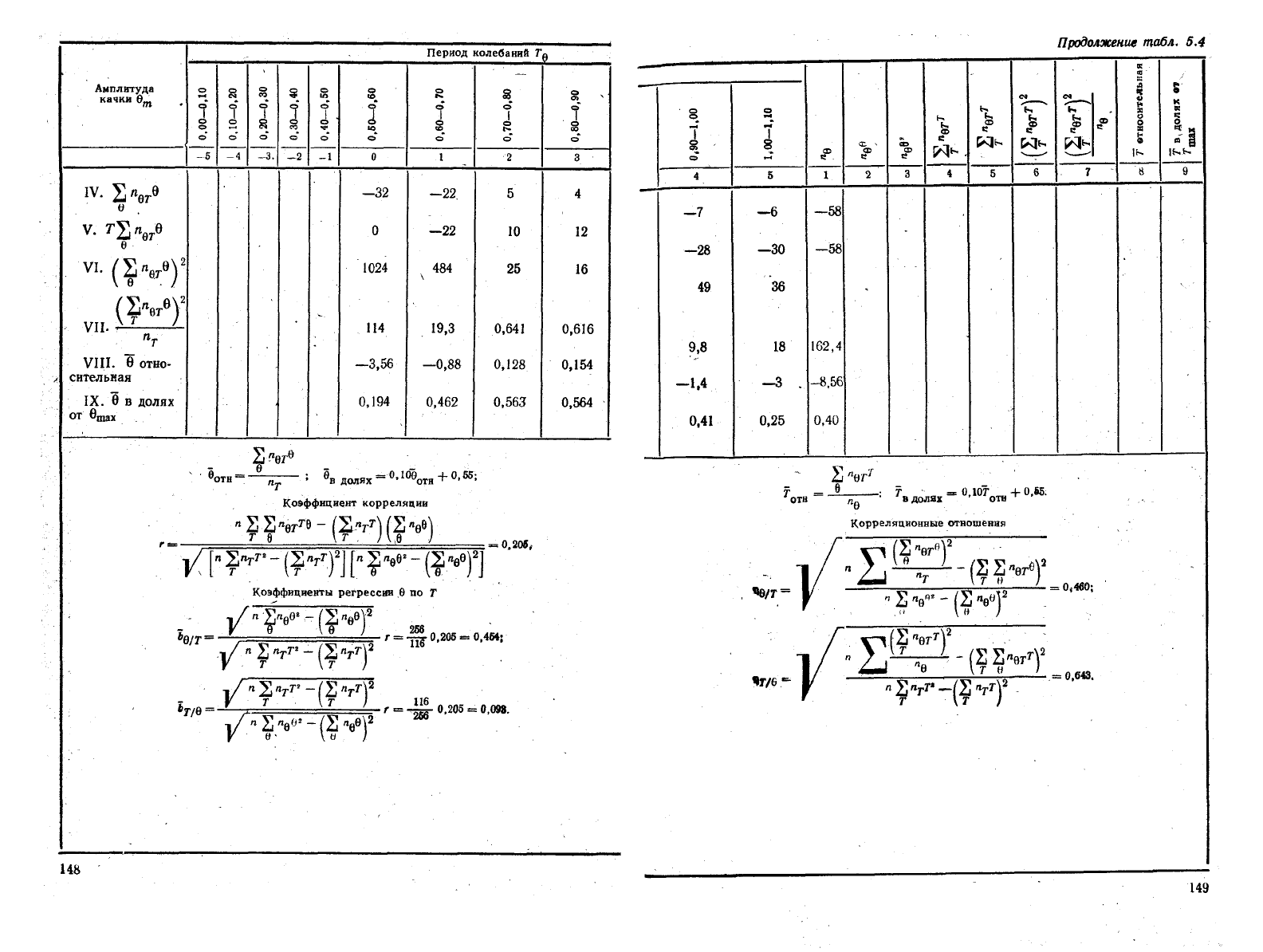
зом (табл. 5.4):

2."

Это значит, что амплитуде 6

в пределах

0,00—0,10

ее максимального значе-

ния

соответствуют два наблюдения обработанной записи при периоде

0,50—0,60

максимального' значения, —10 есть произведение 2-(—5), где —5 сомножитель

первой строки, 0 — произведение 2-0, где 0 — сомножитель соответствующего

столбца периодов

(0,50-^-0,60)

(см. табл. 5.4).

Пример

расчета (табл. 5.4). Анализ качки судна

«Метеор»

на нерегу-

лярном

волнении. Испытания проводились под руководством академика А. Н Кры-

лова в Атлантическом океане 9 марта 1913 г. Водоизмещение судна

3955

т, попереч-

ная

метацентрическая высота h = 0,8 м, скорость 9 уз, максимальная высота, волны

12,2 м, максимальная амплитуда бортовой качки Э

шах

= 25°, максимальный пе-

риод

шах

= 19 с.

Коэффициент

корреляции равен

0,205,

что показывает на нелинейную зависи-

мость

углов

крена и периодов качки (для независимых величин коэффициент корре-

ляции

равен нулю, для линейной зависимости — единице). Среднее значение ампли-

туд

угла

крена 8=

0,40-9

шах

= 10°, средний период TQ = 0,741

•

Т^тях

14,1с.

§ 21. МЕТОДЫ

СТАТИЧЕСКОЙ

ОБРАБОТКИ

ВИДИМЫХ

ЭЛЕМЕНТОВ

СЛУЧАЙНОГО

ПРОЦЕССА

видимым элементам случайного процесса относят амплитуду, размах, период.

От того, как определен' тот или иной элемент, зависит

результат

статического ана-

лиза.

В настоящее время применяются следующие элементы:

амплитуда а (рис. 5.6, а) — расстояние по оси х от экстремума до линии мате-

матического ожидания х, причем амплитуда имеет знак минус, когда экстремум

обращен выпуклостью к линии математического ожидания (вторичный экстремум);

размах А

(рис. 5.6, б) — расстояние по оси х

между

ближайшими максимумом

минимумом (с учетом вторичных экстремумов);

размах к

(рис. 5.6, в) — расстояние по оси х

между

ближайшими максимумом

и-даинимумом, которые лежат по разные стороны линии математического ожидания *

(без

учета

вторичных экстремумов);

период x

(рис. 5.6, б) — удвоенное расстояние по оси t

между

двумя ближай-'

шими

экстремумами (с учетом вторичных экстремумов);

период т

(рис. 5.6, в) — удвоенное расстояние по оси t

между

ближайшими

максимумом и минимумом, лежащими по разные стороны линии математического

ожидания

* (без

учета

вторичных экстремумов);

период т

(рис. 5.6, г) — расстояние по оси t

между

ближайшими максимумами

(минимумами);

период т

(рис. 5.6, д) — удвоенное расстояние по оси t

между

ближайшими

пересечениями линии математического ожидания х с функцией х (О-

Можно

ввести также дополнительные определения

ft 2o аН; о Л

Для оценки морского волнения гидрометеорологи пользуются h

и T

, кото-

рые х достаточной для практики точностью, как показала экспериментальная

152