Благовещенский С.Н., Холодилин А.Н. Справочник по статике и динамике корабля. Динамика корабля. Том 2

Подождите немного. Документ загружается.

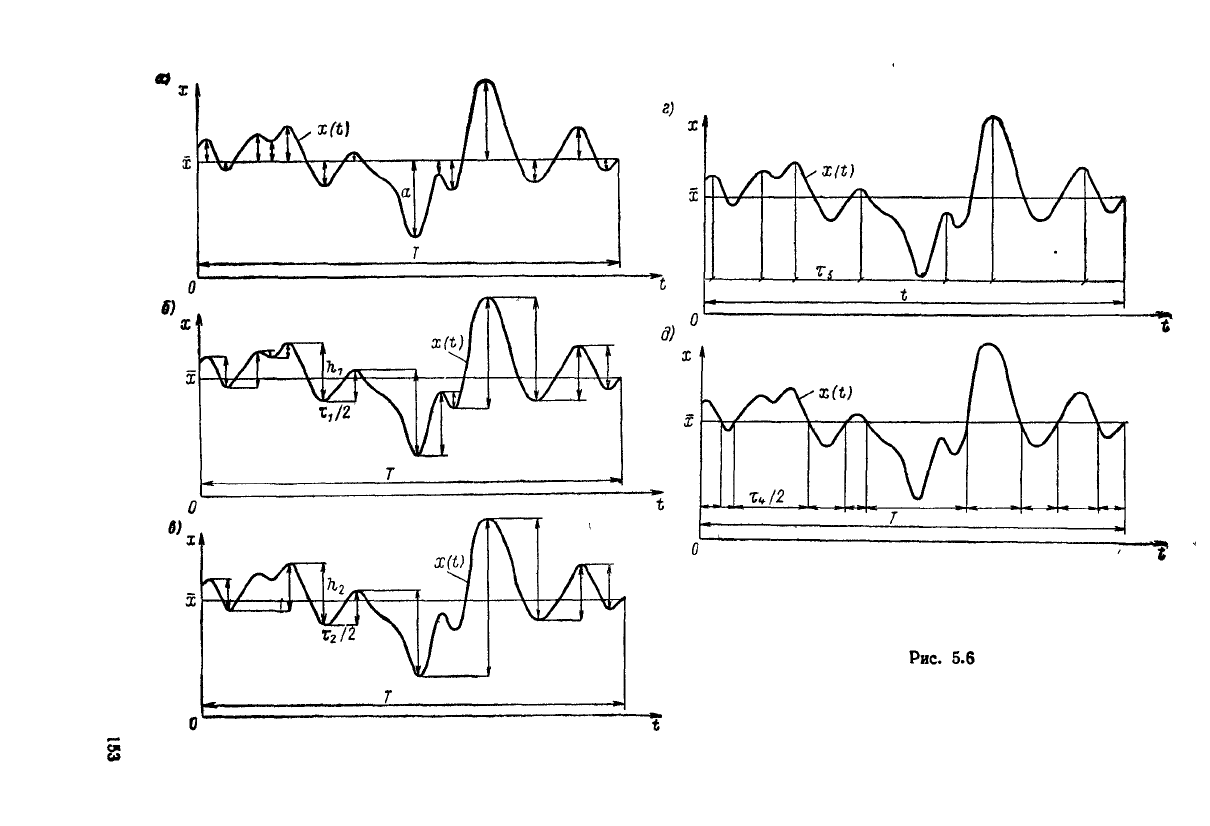
Рис.

5.6

проверка, характеризуются формулами

Uh)

ехр

(- Si

где А

]/~2nD

— дисперсия процесса

-(-i-H*)

Формула (5.9) предложена Ю. М. Крыловым. Формулы (5.8), (5.9) и

(5.10)

справедливы только для волнения, но ими, как правило, пользуются и при обработке

записей

качки. '

Из

закона распределения Раиса

следуют

зависимости

а =

1,25

УП^УТ^И?;

£*[0,57в«

+ 0,43 J,

где е — ширина спектра.

Если

известны а и D

(как

результат

обработки процесса), то по ним можно

точно определить D

и, е

- 2а

0,363a*;

e = -_ / 1 —

Лонге-Хиггинсом была показана связь средних значений периодов т

и т« с мо-

ментами спектра нормального случайного процесса

где т, определяются по формулам, приведенным в главе 1.

Имеют места следующие зависимости:

п*

(б.И)

для стационарных случайных процессов.

Подобный

анализ различных методов обработки записей нерегулярного про-

цесса был проведен А. Н. Балакиным. Он показал, что если целью обработки

является получение моментов спектра, т. е. спектральных характеристик случай-

ного процесса, то обработку

следует

вести по амплитудам с и периодам т

и т

(для

данной

задачи выбор определения периода не имеет значения, однако он определяет

используемые при этом формулы).

Необходимо иметь в

виду,

что у процесса, имеющего узкий спектр е = 0,

отсутствуют

вторичные экстремумы, а следовательно, высоты ftj и ft

перестают

154

отличаться

друг

от

друга.

Поэтому погрешность в этом

случае

состоит не в

методе

обработки записи, а в исходных формулах вследствие неучета ширины спектра.

Для одной и той же реализации ft

> ftj и х

>"т

, поэтому более опасную

ошибку

дают

величины h

(занижают

амплитуду)

и т

(завышают периоды, следо-

вательно, занижают ускорения)

При

анализе характера качки судна часто проводят сравнение средней ампли-

туды

качки, "полученной расчетом, со средней амплитудой качки, зарегистрирован-

ной

во время проведения натурных испытаний. Обычно бортовая качка как выход-

ной

процесс имеет более узкий спектр, чем входной процесс — волнение. Поэтому

ошибка

от применения того или иного метода при расчетах бортовой качки с узким

спектром невелика. Для уменьшения ошибки

следует

обрабатывать амплитуды а,

а не размахи h

или Н

. При этом

следует

сравнивать не амплитуды, а дисперсии

качки

— расчетную и полученную.

В некоторых

случаях

при обработке реализаций случайных процессов инте-

ресуются связью

между

размахами и соответствующими им полупериодами. Если

обработку

ведут

по амплитудам а и периодам т

или т

, то эту связь обнаружить не-

возможно, поэтому для отыскания ее необходимо пользоваться высотами h

или

и периодами tj

ИЛИ

. Причем метод, учитывающий наличие вторичных экстре-

мумов /ц, т

предпочтительнее, поскольку совместный закон распределения раз-

махов и периодов получен именно для этого метода.

Если при производстве обработки процесса интересуются лишь статистикой

размахов, не ставя целью получение спектральных характеристик, то в этом

случав

можно использовать любой метод, обязательно указав при этом, каким из них эта

статистика получена. Так, при анализе бортовой качки модели в полунатурных

условиях на открытом водоеме удобнее пользоваться высотами h

и периодами х

поскольку такая обработка автоматически исключает низкочастотную составляющую,

которая,

в данном случае, незначительно влияет на бортовую качку, но существенно

усложняет обработку по Н

и т

При

анализе килевой качки в тех же условиях потеря информации о длинных

волнах может существенно исказить

результат

эксперимента, поэтому здесь обра-

ботка должна вестись по ft

и т

Приведенные рекомендации А. Н. Балакина

следует

учитывать при обработке

записей

волнения и качки судна.

При

рассмотрении задач качки

судов

предполагают, что случайные функции

стационарны

в широком смысле. При этом математические ожидания постоянны,

а корреляционные функции зависят только от разности аргументов, а не от их ве-

личины.

Под

стационарным процессом в узком смысле понимают такой процесс, когда

все без исключения вероятностные характеристики случайных функций инвариантны

относительно произвольных сдвигов по оси независимой переменной (обычно вре-

мени).

Спектральная плотность и корреляционная функция связаны формулами

Винера-Ханчина

(о) = — f К

(т) cos at dx;

со

x (a) cos oi da,

где S

(a) — спектральная плотность процесса x; K

W — корреляционная функ-

ция

процесса х; а — частота; т = <

— *

— разность аргумента — времени <

и t

Стационарный

процесс называется эргодическим, если его числовые характе-

ристики,

полученные усреднением по множеству реализаций с вероятностью, сколь

угодно близкой к единице, равны тем же числовым характеристикам, полученным

усреднением по времени из одной достаточно длинной реализации случайного про-

цесса.

В теории качки

судов

на нерегулярном волнении все процессы предполагаются

стационарными

в широком смысле и эргодическими.

155

Среднее значение стационарной случайной функции равно

lim

—

П->00

а стационарной

эргодической равно

-±r f

x(t)dt.

Стационарная

случайная функция

постоянной спектральной плотностью

на-

зывается белым шумом

(т) =

2JIS

(T),

где

const

—

спектральная плотность,

(т)

5Г

"ЗГ

cos

rfa>

—оо

—

функция Дирака.

Во многих задачах качки рассматривается совместно несколько случайных

процессов.

Для

характеристики

двух

случайных функций

(f)

и Y (?)

исполь-

зуют

взаимную корреляционную функцию

tt П =

{(X

- М

(01

[У (П

- M

U')]},

где

Мх

(О

-My

(?)

—

математические ожидания функций

(/)

и Y

(/');

? —

произвольно выбранные значения аргументов

Всегда

t)Ky(t',t'),

где

Z?x (О

(?)

—

соответствующие дисперсии

Нормированная

взаимная корреляционная функция

(t)£y(?)\

При

(?)

= Y (?) —

автокорреляционная функция

Кхх

М {[X

(/) — Мх

(01

[X (?) — Мх

(?)]}•

Если

взаимная корреляционная функция случайных функций

(/)

и Y

(()

на

равна тождественно нулю,

то

случайные функции

(i)

и Y

называются корре-

лированными,

если равна нулю

—

некоррелированными

Взаимная спектральная плотность равна

со

(w)

-i-

iax

(т) dx

(о)

QxY

«>),

—да

где

CXY

(—

°)

Сух (a)

= a

(o)

—

cospectrum

—

реальная часть спектра,

QxY

(с)

—QXY

(—

°")

—'QYX (

)

—-quadrature spectrum

—

мнимая

часть

Y(°)\-

156

Для вещественных случайных процессов

DXY

= KXY

(0)

= | C

(a) dv

Коэффициент

когерентности равен

v (a\

[CxY {a

xyK

(a)]

(O)J

Если

этот коэффициент равен единице, имеет место линейная зависимость

си-

стемы, если

(о) =0, два

процесса

(0 и

(t)

статически независимы. Практи-

чески линейную зависимость принимают, начиная

0,86

МЕТОДИКА

ОБРАБОТКИ

АНАЛИЗА

ПЕРВИЧНЫХ

МАТЕРИАЛОВ

НАТУРНЫХ

ИСПЫТАНИЙ

СУДОВ

Первичными

материалами натурных мореходных испытаний являются записи

(реализации)

исследуемых процессов, представленные

виде осциллограмм

или

диаграмм лент Задачей обработки первичных материалов является получение спек-

тральных

вероятностных характеристик процессов

предположении,

что

послед-

ние

являются стационарными

эргодичными,

закон распределения

их

ординат

нормальный

Спектральный

анализ. Реализацию процесса

(/)

представляют

виде дискрет-

ного набора ординат, снятых через равные промежутки времени

А/. Шаг по

времени

Д? выбирают

из

расчета,

что Q

2л/Д/

(частота Найквиста) есть частота,

по

край-

ней

мере вдвое превышающая частоту наиболее высокочастотной составляющей

дан-

ного процесса Представление, графика

(/)

виде ряда

, где

—

номер снимае-

мой

ординаты, осуществляется

помощью серийного фотодешифратора графиков

«Силуэт»

или

вручную

случае

применения

«Силуэта»

процесс сразу заносится

на

перфоленту

может быть введен

ЭЦВМ

для

дальнейшей обработки.

Косвенный

метод Метод реализует вычисление спектральной плот-

ности

по

формулам, структура которых предполагает использование ЭЦВМ.

Спектральная

плотность

по

частоте

определяется

по

формуле

где

-2

(р)

cos

£^L

+ R{m) cos

Ли;

— 1,

I, .. .

(6.12)

,-X)(X^-X);

= 1, 2, ...,

п.

Здесь

X = —;

N —

общее число ординат

данной реализации;

157

— длительность реализации (время записи); т = рД< — сдвиг по времени

(аргу-

мент автокорреляционной функции); х^ях = тЫ — максимальный сдвиг по вре-

мени.

Рис.

5.7

Максимальный

сдвиг по времени определяется следующим образом. Отыски-

вается такое значение т = т^ при котором огибающая функция R (т) имеет первый

минимум

ИР

(

)

шах

mIn

= при т = T

(5.13)

ша

принимается такое ближайшее к т

значение т, при котором автокорреля-

ционная

функция равна нулю (рис. 5.7).

Для сглаживания спектра используется интерполяционная" формула И. Ханна

5* (о

) =

0.25S

) +

+0,55

(а

) +

0,255

(а

к+1

)

или

В. Хамминга

S* (а

) =

0,235

(а

) +

-f

0,545

(о

) +

0.23S

(а

к+1

целью оценки достоверности

спектральной плотности, вычисленной

по

реализации конечной длины, рас-

считываются доверительные пределы

для ординат спектральной плотности

(рис.

5.8). Между нижним и верхним

пределами, вероятность превышения

которых составляет соответственно 95

5%, заключена 90%-ная довери-

тельная область, в пределах которой

рассматриваемая ордината спектра

будет

заключена в 90

случаях

из 100. Число степеней свободы г, определяемое ра-

венством г =

27Ут

= 2Nlm, может рассматриваться как мера достоверности

спектрального анализа, что имеет значение при сопоставлении результатов опреде-

ления

S (а) по реализации различной продолжительности.

Прямой

метод. Спектральная плотность по частотам о

= 2яЫ_Т опре-

деляется формулой

Рис.

где коэффициенты разложения Фурье С

подсчитывают по формуле

п—0

168

Выражение для S (а

) носит название «периодограмма». Для получения более

состоятельной оценки S (а^ периодограммы усредняют следующим образом:

по

временным интервалам

q=0

». e. весь ряд Х„, содержащий N членов, разбивается на п

интервалов с номерами q;

подсчитываются периодограммы для каждого интервала, и ординаты периодограмм

одинаковыми номерами k усредняются по п

интервалам;

по

частотам

кл'

si2)

^=W+wmL

(5Лб)

k-n, •

в. отыскивается среднее значение ординат периодограммы по (2л

+ 1) точкам,

эта

операция

соответствует

нахождению скользящего среднего-

Рис.

5.9

Для оценки достоверности S (а), полученного прямым методом, можно поль-

зоваться доверительными пределами, приведенными на рис. 5.8, причем число сте-

пеней

свободы г

будет

= 2п

Параметры усреднения п

и л

выбирают такими целыми числами, чтобы выра-

жение

„2„2

1 ft • тцъ

было наименьшим. Здесь Тш^ — время затухания автокорреляционной функции,

выбираемое согласно условию (5.13); Г — время реализации; /— интервал (частот)

практического существования спектра. '

Этим выражением пользуются в том

случае,

когда указанные параметры

известны заранее, или после предварительного расчета.

Если для вычисления С

применяется алгоритм, построенный на принципе БПФ

(быстрое преобразование Фурье), то прямой метод является более экономичным

смысле экономии машинного времени, нежели косвенный.

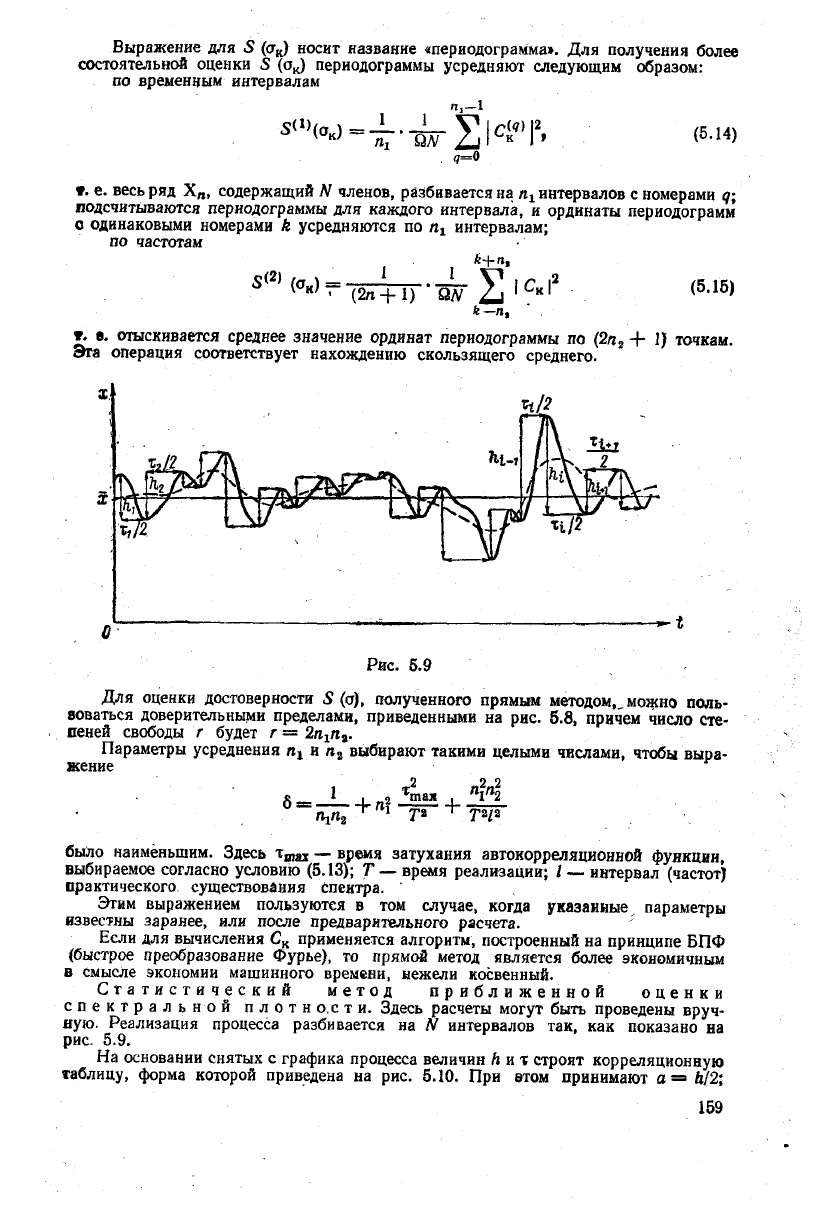
Статистический метод приближенной оценки

спектральной плотно.сти. Здесь расчеты

могут

быть проведены

вруч-

ную. Реализация процесса разбивается на W интервалов так, как показано на

рис.

5.9.

На

основании снятых с графика процесса величин h и т строят корреляционную

таблицу, форма которой приведена на рис. 5.10. При втом принимают а = й/2;

159

(5.16)

2т72.

Здесь I — разряды периодов т, f — разряды амплитуд а, щ — количество

амплитуд, отвечающих условиям

(/ — 1) Да <3 a/ <J /Да;

(< — 1) Дт <3 xi <S (Дт,

где Ат — величина интервала (шаг) разряда периодов; Да — величина интервала

(шаг) амплитуд; т — верхняя граница разрядов амплитуд, в который попала хотя

бы одна амплитуда; /— верхняя граница разрядов периодов.

Спектральная плотность в интервале частот

2я . _ . 2я

(i-l)

определяется по формуле

Д l

17)

Расчет выполняется в табличной форме

Если спектр процесса широкий, то делается второе приближение: ,Для этого

через середины высот проводят кривую, которая является текущей средней Эта

кривая

обрабатывается таким же образом

до получения спектральной плотности S

(a).

Спектры S (а) и S

(а) суммируются При

необходимости можно сделать еще ряд при-

ближений Полученная таким методом оценка

спектральной плотности тем точнее, чем ^же

спектр процесса и чем больше длина реали-

зации

Число снимаемых ординат должно

быть несколько сотен

Пример

расчета Обработка

реализации записи бортовой качки судна.

На

рис 5. И, а приведена часть реали-

зации

процесса. Под математическим ожи-

данием понимаем в (горизонтальная пря-

мая).

В частности, это может быть О'или ста-

тический

угол

крена судна, около кото-

рого происходит качка. Снимаем размахи

углов

крена h

, h

, ... и соответству-

ющие им полупериоды Tj/2, Та/2, Тз/2 и т д Полученные значения последовательно

записывают в условных единицах измерения, например в миллиметрах.

Значения

;

HI,

{

мм т

(

/2, ми

m-i

Пет

г Г Ч - • I

Рис.

б. 10

6-1

е ~х

Составляем корреляционную таблицу (табл. 5.5). Заносим в нее количество заме-

ренных значений, исходя из условия (5.16). В нашем примере шаг Да = 1,25 мм

(0,4125

град); Дт

=•

Б.00 мм

(0,935

с); а

/Aaf

«Дт.

160

Определяем спектральную плотность 5 (о

(

) по

формуле

(5.17), она

отличается

от значения G, (строка VI табл. 5 5) на постоянный сомножитель (1/2) п.

Делаем второе приближение, проводя кривую ~6 через середины ордина-i

(рис.

5.11,6)-

Эта кривая является текущей средней. Обрабатываем ее таким же

образом до получения спектральной плотности 5, (<л) или G*, отличающуюся на

постоянный

сомножитель (1/2) я Строим корреляционную таблицу для второго

приближения

(табл 5.6).

Суммирование спектров приведено в табл 5.7.

Дисперсия определяется интегрированием по частотам, в предположении, что

пределах каждого интервала частот (неравномерных) функция постоянна.

В табл. 5.7:

_рч 1__ Да/ 1 1 .

~2п ~ ~&Г' ~2я Дх(| —1) ~ Дг« '

Здесь Дт = 5 мм в Да - 1,25 мм.

Для получения размерности D, трал

необходимо умножить D на коэффициент

Аа

А*

(1,25-0,33

град)»

(5-0,187

с)

-~ДГ~

5-0.187С

°'

17 Град

Вероятностный анализ. Вероятностные параметры качки вычисляют по эмпири-

ческим функциям распределения и статистическим вероятностям с помощью корре-

ляционной

таблицы

Функцию

распределения амплитуд подсчитывают по формуле

|>;

w-^nv—»

5Л8)

/ m

где N = У\ ^ пц — общее число амплитуд, снятое с графика. Обеспеченность вы-

числяют так. F,y =1 — F/.

Среднюю амплитуду определяют формулой

(5.19)

Дисперсия амплитуд

Д,

Да«>

р, (/ —£- -> P. [l-v) •

(5-20)

Среднее квадратическое отклонение амплитуд (стандарт)

Ста - VD

Коэффициент

вариации амплитуд

161

20.