Благовещенский С.Н., Холодилин А.Н. Справочник по статике и динамике корабля. Динамика корабля. Том 2

Подождите немного. Документ загружается.

\\>

\1\

\я

—'в

9р

•~~

~»

——•

2ft

"-.

"-•

"—.

с—

ч,

S.0

о,7

0,8

о?

1,0

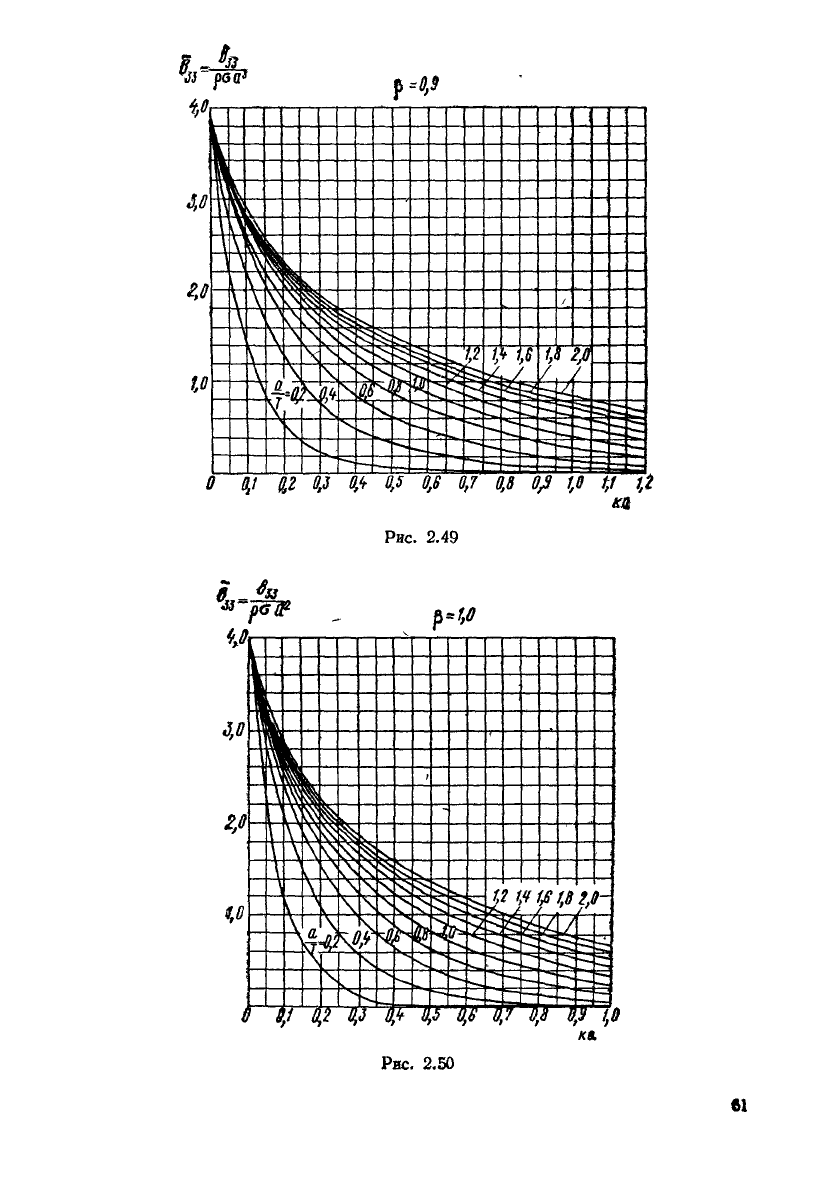
Рис.

2.49

Рис.

2.50

2,0

0,5

1 1

—,

1,2

Ifi

1,6

•*—

-3

W£

—.

—-

——

*——

0,1

0,2

0,3

0,4

0,5

0,8

0,7

0,8

0,3

1,0

1,1

1,2

ка

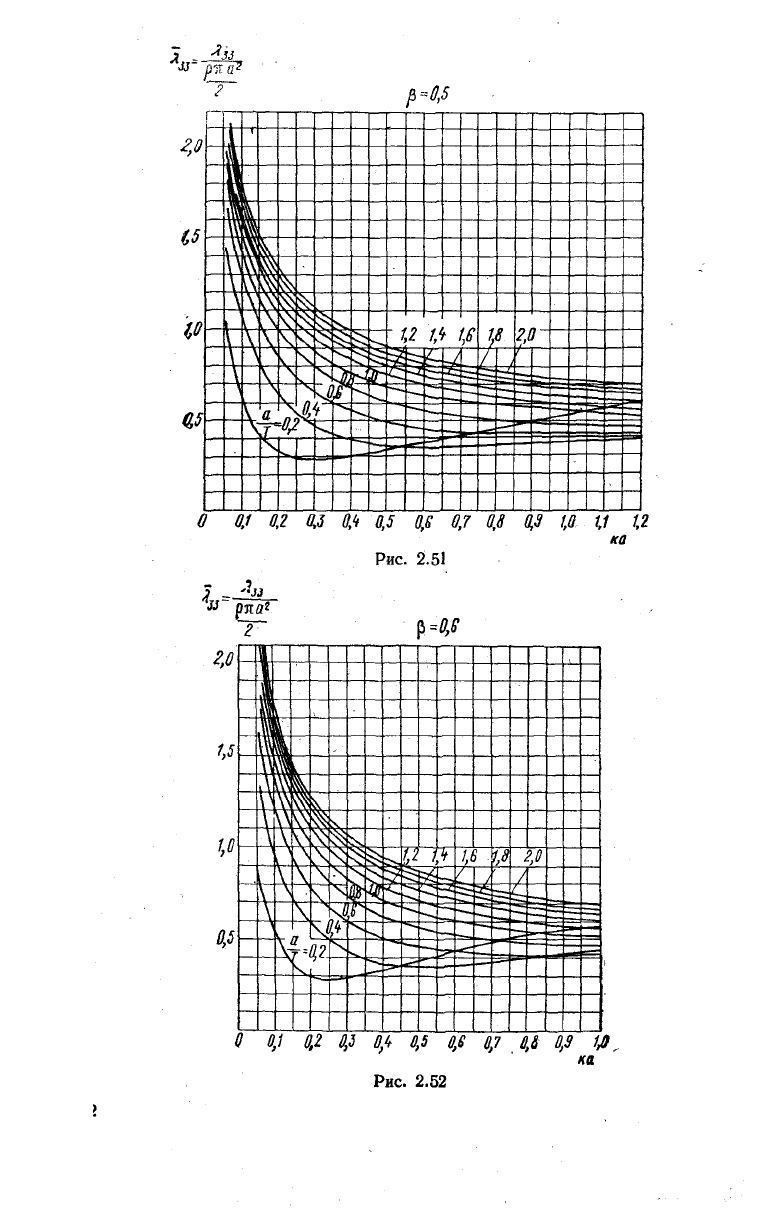
Рис.

2.51

0,1

0,2

0,3

0,k

0,5

0,S

0,7

0,S

0,3

1ft,

ка

Рис.

2.52

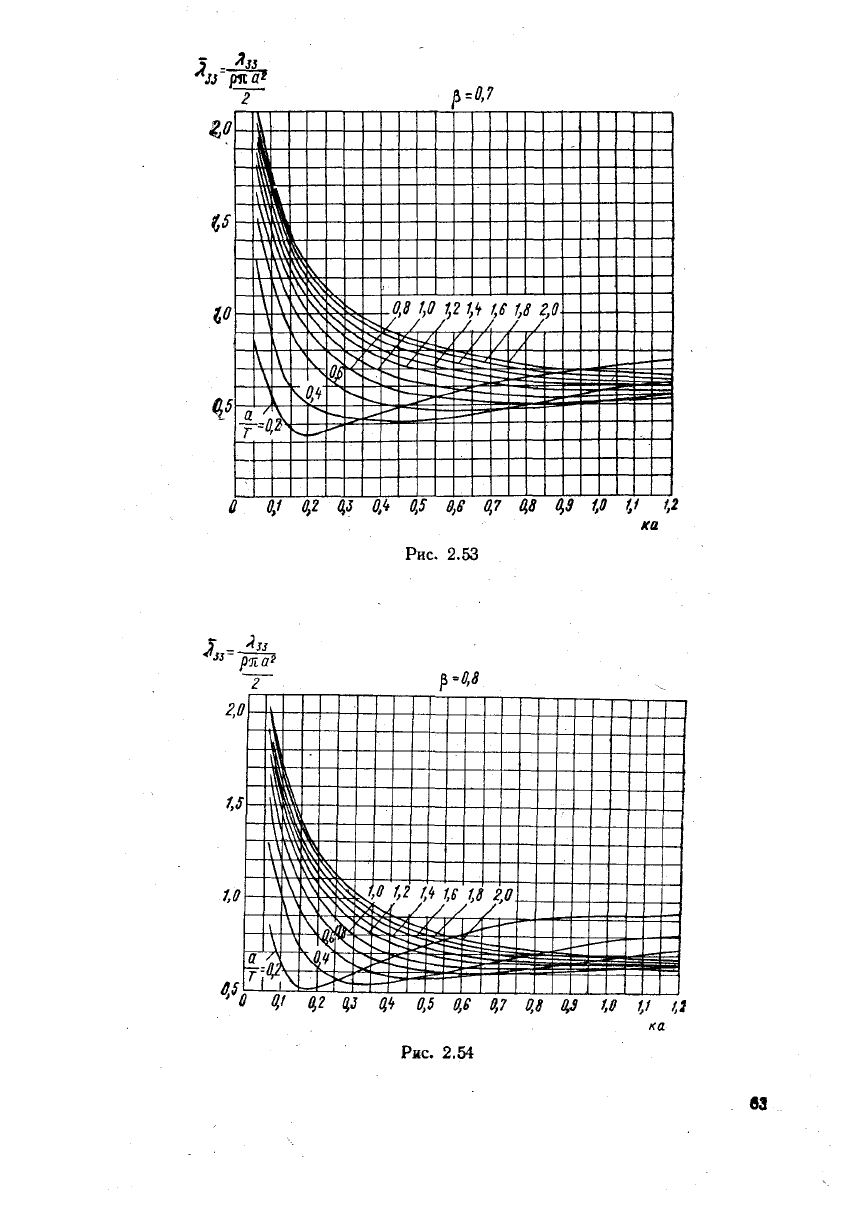
Рис.

2.53

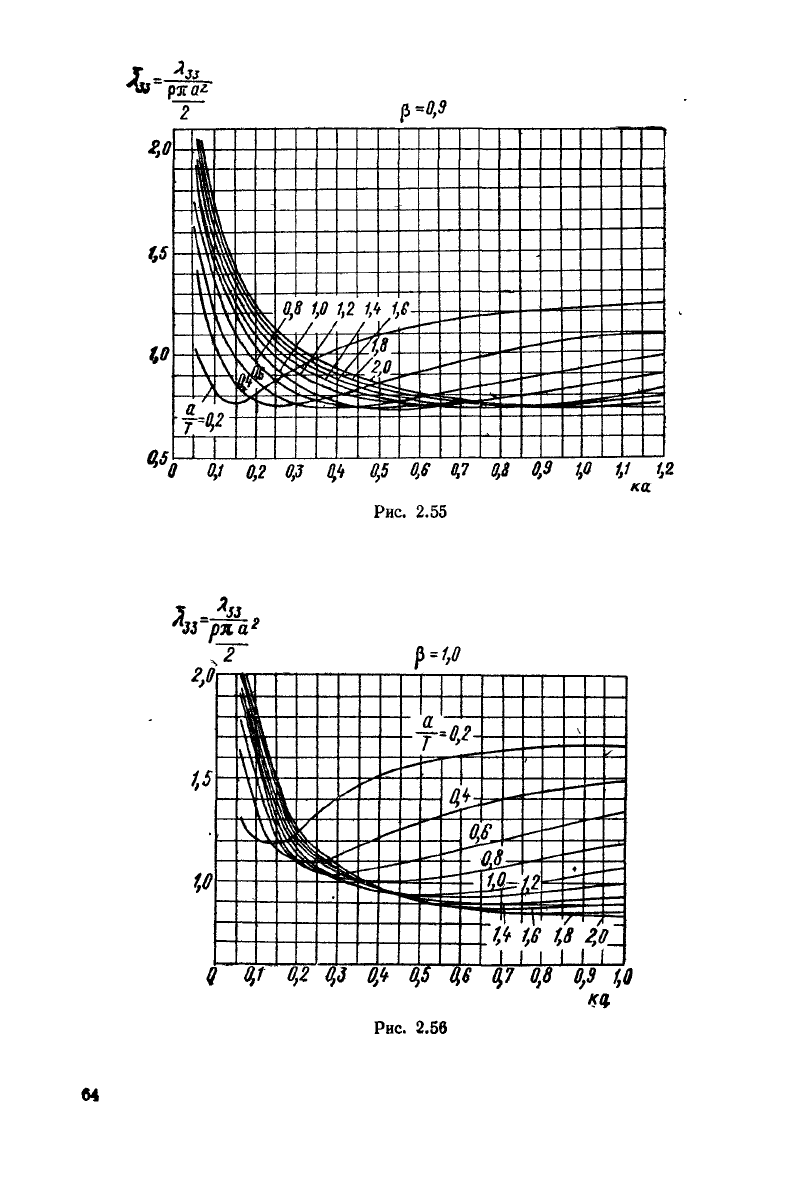
Рис.

2.55

Рис.

2.5f

полуширине ГВЛ и распределения площади по высоте. Вычисленные характери-

стики

помещены в 21 таблицу, из которых, в частности, можно определить Ь

s- Сопроводительный'текст переведен, а графики и таблицы полностью приведены

известной монографии И. К- Бородая и Ю. А. Нецветаева «Качка судов, на мор-

ском

волнении», Л., «Судостроение», 1969. Поэтому эти материалы в настоящем

справочнике не приводятся.

Экспериментальные методы. Многие исследователи проводят экспериментальное

определение коэффициентов присоединенных масс и сопротивления в широком диа-

пазоне

вариаций главных размерений судна. Впоследствии полученные результаты

рекомендуются для широкого применения. Однако, как правило, такие результаты

представляют ограниченный интерес, ввиду ограниченного объема эксперименталь-

ного исследования и не

могут

иметь универсального характера. В качестве примера

приведем работу Геритемы из доклада Комитета по мореходным качествам 13 Меж-

дународной конференции опытовых бассейнов (Берлин—Гамбург,

1972).

В этой работе сравниваются современные методы расчета с методом Корвин-

Круковского для продольной качки корабля.. Говорится об экспериментальном ис-

следовании, проведенном с моделями судна 60-й серии, с широким диапазоном вариа-

ции

L : В от 4-х до 20, числа Фруда в процессе опыта принимались равными 0,15;

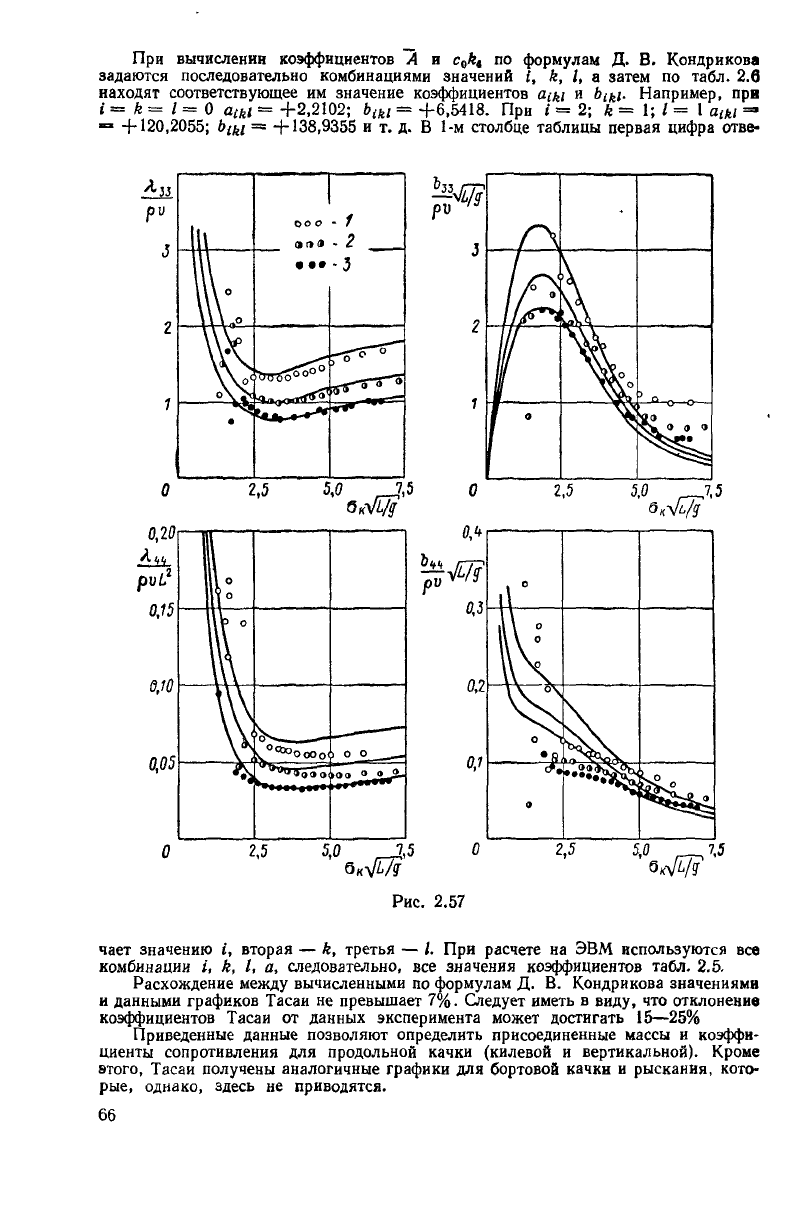
0,20 и 0,30. На рис. 2.57 приведены результаты сравнения значений присоединенных

масс и коэффициентов сопротивления, полученных расчетом и опытом ( 1 =- =4;

=—=5,5;

3 — = 7). Как видно, совпадение удовлетворительное.

о )

Метод Тасаи. Результаты Ф. Тасаи наиболее близко совпадают с экспериментом

из

существующих методов расчета. В исследованиях Тасаи рассматривается цилиндр

совершающий вертикальные колебания в потенциальном потоке. В

результате

вы-

числения

получены графики коэффициента А, равного отношению амплитуды про

грессивной волны к амплитуде волны, вызванной вертикальной качкой, и

j(r

гдес

—

отношение присоединенной массы цилиндра при бесконечной частоте колебания

массе цилиндра единичной длины, k

— отношение присоединенной массы цилиндра

заданной частоты к произведению с

на массу цилиндра единичной длины.

Тасаи получена серия графиков в функции частотного коэффициента £

(aVg) Т — kT, где а — частота колебаний, Т — осадка, g — ускорение силы

тяжести. На каждом из графиков представлена серия кривых в функции отношения

= В/2Т, где В — ширина судна, и р" — коэффициент полноты рассматриваемого

шпангоута.

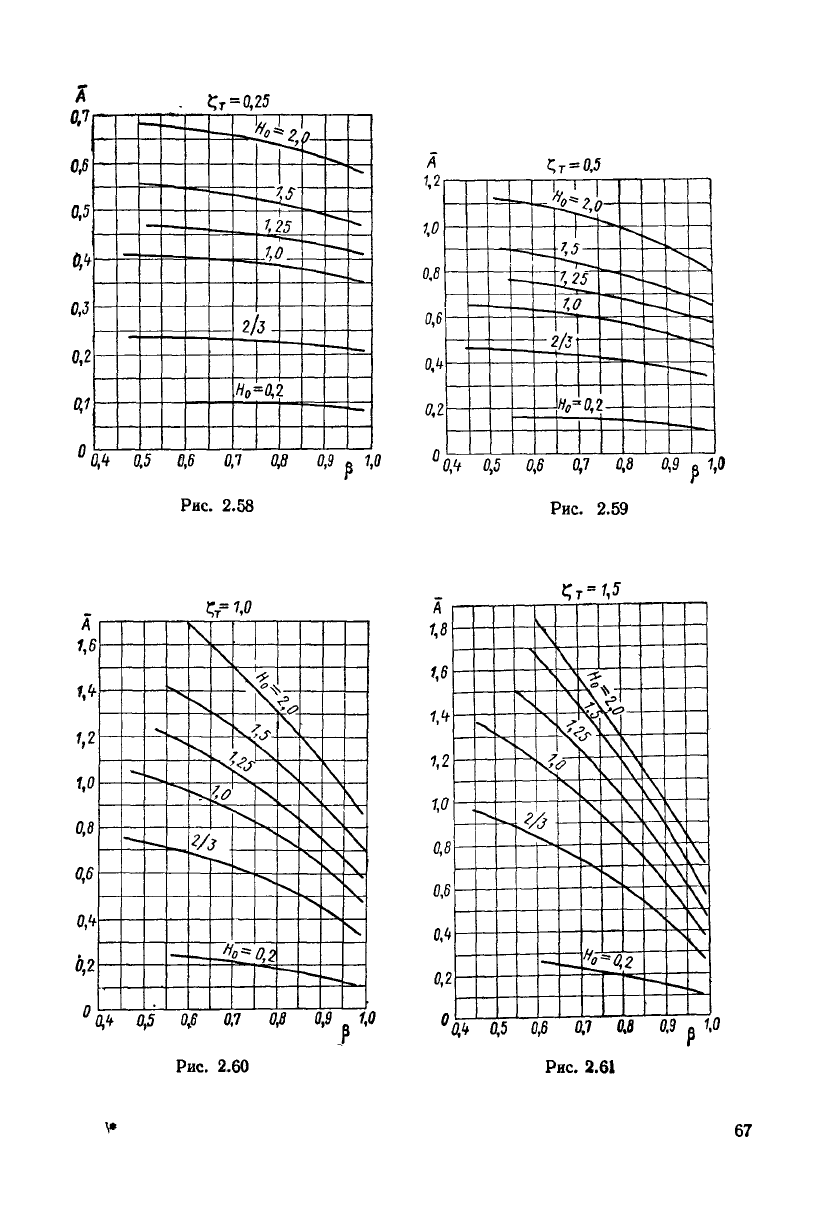
Сопротивление и присоединенная масса на единицу длины судна вычисляются

по

формулам

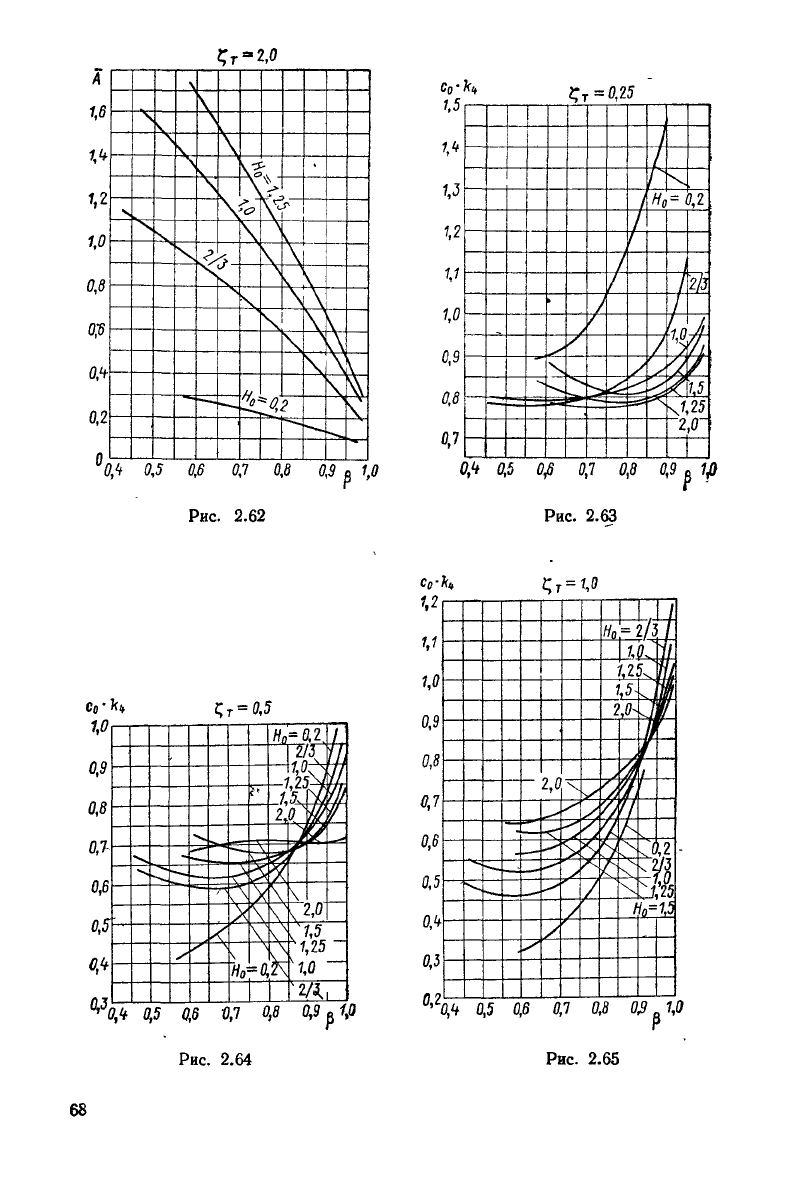
где А снимают с графиков рис.

2.58—2.62;

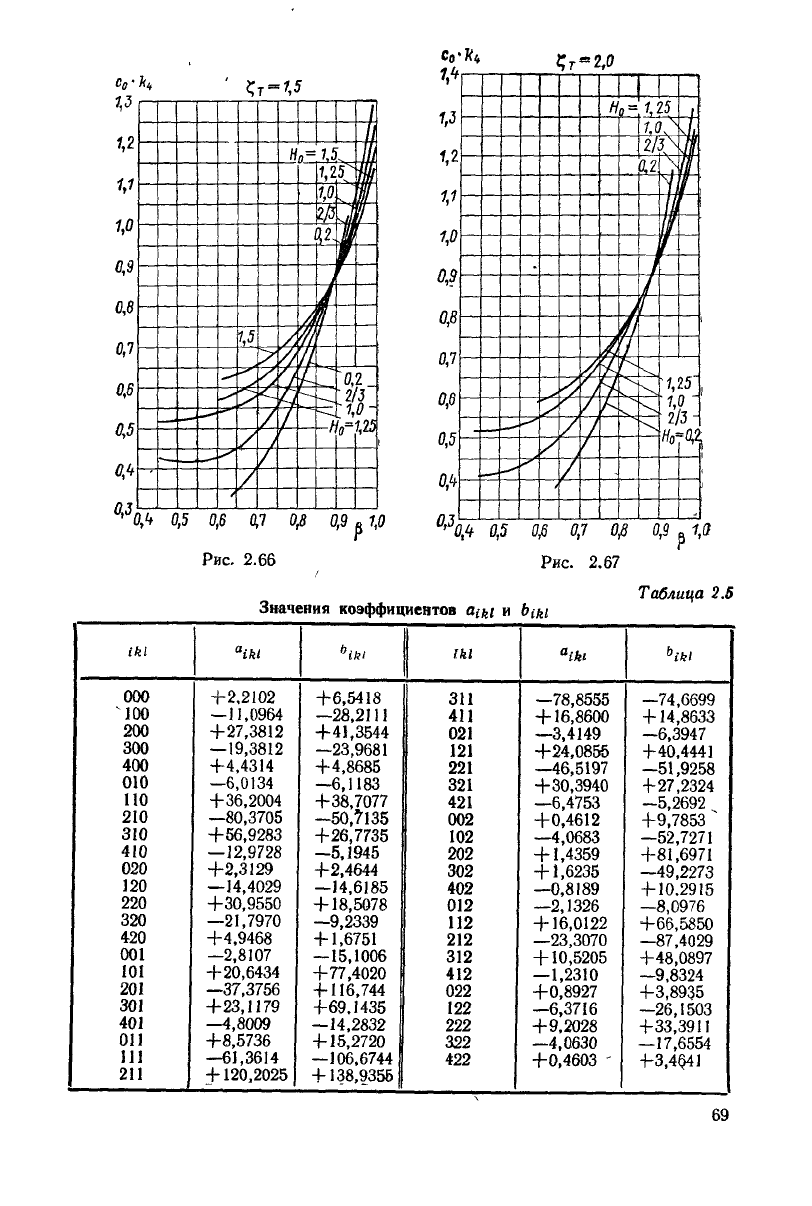
а значения

с графиков рис. 2.63—

2.67. Полные значения присоединенных масс и сопротивления определяют обычным

путем — интегрированием по длине судна, т. е. и в этом

случае

применяется метол

плоских сечений.

Д. В. Кондринов получил аппроксимирующие формулы по графикам Тасаи,

что позволило ему вести непосредственный расчет на ЭЦВМ. Коэффициенты аппрок-

симированы полиномами вида

1=0

*=0 1=0

*-2

•**(*)'«•.

t=0

6=0 /-=0

Значения

коэффициентов a^i и b^i вычислены (см. табл. 2.5).

3 С Н Благовещенский, А. Н. Холодилвн 65

При

вычислении коэффициентов А и

по формулам Д. В. Кондрикова

задаются последовательно комбинациями значений I, k, l, а затем по табл. 2.6

находят соответствующее им значение коэффициентов aiu и btki- Например, при

= k = / = 0

- +2,2102; Ь

= +6,5418. При « = 2; k = 1; / = 1

=»

•» +120,2055; b^i = +138,9355 и т. д. В 1-м столбце таблицы первая цифра отве-

•

оо о

• ••

• 1

• 2

•3

0,05

I о

•

>^0

в о •

2,5

5.0

0,1

•я

2,5

5,0

Рис.

2.57

чает значению i, вторая — k, третья — /. При расчете на ЭВМ используются все

комбинации

i, k, I, а, следовательно, все значения коэффициентов табл. 2.5.

Расхождение между вычисленными по формулам Д. В. Кондрикова значениями

данными графиков Тасаи не превышает 7%. Следует иметь в виду, что отклонение

коэффициентов

Тасаи от данных эксперимента может достигать 15—25%

Приведенные данные позволяют определить присоединенные массы и

коэффи-

циенты

сопротивления для продольной качки (килевой и вертикальной). Кроме

этого, Тасаи получены аналогичные графики для бортовой качки и рыскания, кото-

рые,

однако, здесь не приводятся.

0,5

0,2

™

II-

——

—

—-»

1,1

2/j-

Ho"

=0,2

•~^.

•—-

—i—

-*—

—

——.

0,4

0,5

6,6

0,1

OjB

0,9

1,0

Рис.

2.58

0,8

0,6

0,h

0,1

— -

—~-

•— —

— —

—-

"—«

•

-4«

>=;

—-

—

—.

—

0,4

0,5

0,6

0,7

0,8

0,9

1,0

Рис.

2.59

1,6

1,4

1,0

0,8

0,6

0,4

0,2

**-

-~,

•—_

——

—-

0,4

0,5

0,7

Ofi

0,3

1,0

Рис.

2.60

1,4

1,2

1,0

0,8

0,5

0,4

0,2

°0,4

0,5

0,1

0,6

0,9

1,0

Рис.

2.61

1,6

1,0

0,8

0,15

0Л

0,--

——.

ч^

%•

•~~.

0Л

0,5

0,6

0,7

0,8

0,3

1,0

Рис.

2.62

1,5

1,2

1,0

0,3

0,8

0,1

•v

—

^—'

Н„=

0,1

2/3

ч»

1,5

о~

О,

0,5

Ofi

0,7

0,8

0,9

1fl

Рис.

2.63

Со'*

1,0

0,9

0,8

0,7-

0JB

0,5

г*

Но

-Д,

•)

tl2\

У,

^2/^

0,5

0,6

0,7

0,5

0,9,

Рис.

2.64

',2

1,0

0,9

0,8

0,1

0,6

0,5

0Л

0,3

0,2

—

-г

(к

2/3

шли

2,0^

/ч

^ч

ч.

•ч

iff/

•ч./Дг

1,5

'ОЛ

0,5

Ofi

0,1

0,8

1,0

Рис.

2.65

7,3

1,0

0,9

0,8

0,7

0,6

0,5

ЯЛ

0,3

-—»

-—

—-

**•

Ha—

',0^

V-

1,25/

7,0

0,2,

--.

—J

—4

7,7

7,0

0,?

0,8

0,7

0,6

0,5

0,6 0,1 Oft 0,9 p

1,0

0,3^-^

Рис.

2.66

Значения

коэффициентов

a^i и

—

—-*

ТВ

Г,0Л

^2/TN

•O

•*,

2У

25"

-00

Ofi

0,1 Ofi 0,9 p 1,0

Рис.

2.67

Таблица

2.5

ikl

000

MOO

200

300

400

010

110

210

310

410

020

120

220

320

420

001

101

201

301

401

011

111

211

"Ш

+2,2102

—

11,0964

+27,3812

—19,3812

+4,4314

—6,0134

+36,2004

—80,3705

+56,9283

—12,9728

+2,3129

—14,4029

+30,9550

—21,7970

+4,9468

—2,8107

+20,6434

—37,3756

+23,1179

—4,8009

+8,5736

—61,3614

120,2025

+6,5418

—28,2111

+41,3544

—23,9681

+4,8685

—6,1183

+38,7077

—50,7135

+26,7735

—5,1945

+2,4644

—14,6185

18,5078

—9,2339

1,6751

—15,1006

+77,4020

116,744

+69.1435

—14,2832

15,2720

—106.6744

138,9355

ikl

311

411

021

121

221

321

421

002

102

202

302

402

012

112

212

312

412

022

122

222

322

422

lki

—78,8555

16,8600

—3,4149

+24,0855

—46,5197

+30,3940

—6,4753

+0,4612

—4,0683

1,4359

1,6235

—0,8189

—2,1326

16,0122

—23,3070

10,5205

—1,2310

+0,8927

—6,3716

+9,2028

—4,0630

+0,4603

—74,6699

+14,8633

-6,3947

+40,4441

-51,9258

+27,2324

-5,2692

+9,7853

—52,7271

+81,6971

—49,2273

10,2915

—8,0976

+66,5850

—87,4029

+48,0897

—9,8324

+3,8935

—26,1503

+33,3911

—17,6554

+3,4641

0,3

0,1

-==

*—

~~-

»•—

^ —

——

*—-

—

——•

—

—*-

и—-

,_—-

а-ад

SSCS

у"

——•

.—

•в—

0,J

0,2

0,J

0,4

0,5

0,6

0,7

0,8

0,9

1fl

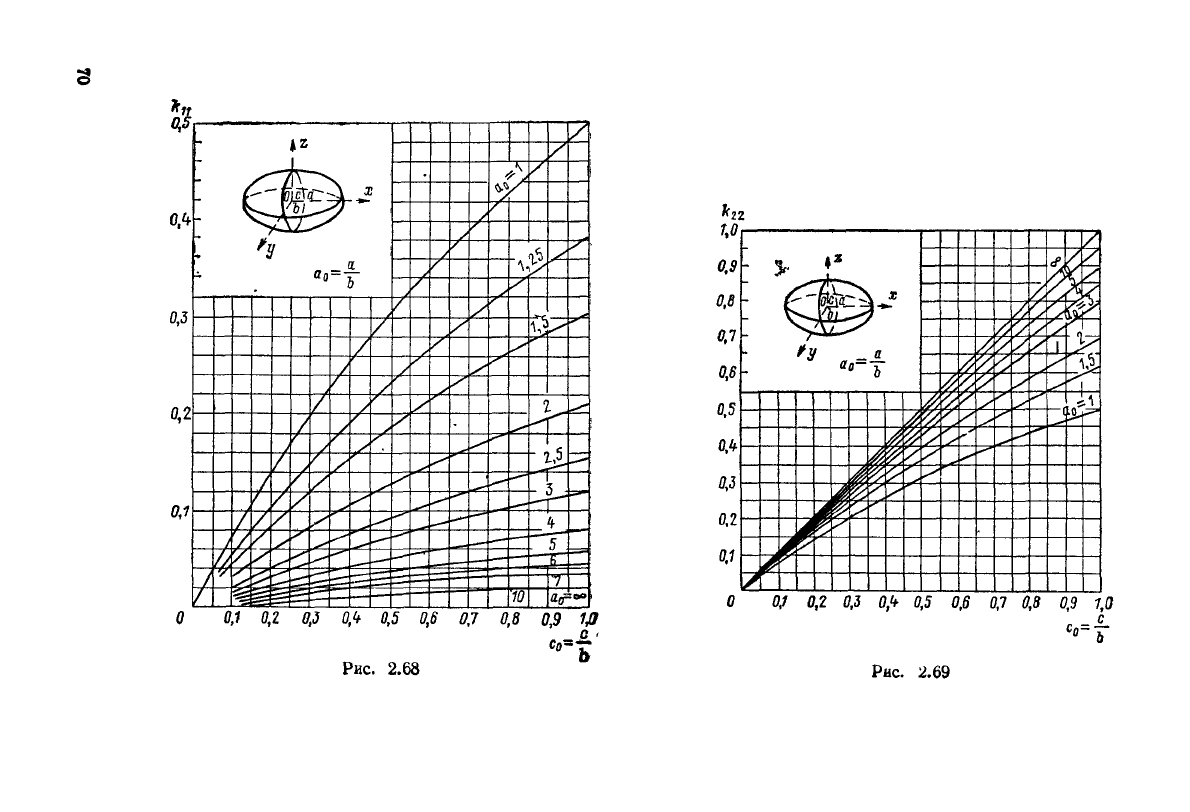
Рис.

2.68

Г,0

0.9

0,8

0,1

0,6

0.5

0Л

0,3

0,1

*У

•y

0,1

0,2

0,3

0,k

0,5

0,6

0,1

0,8

0,9

1,0

. _

Рис.

2.69