Благовещенский С.Н., Холодилин А.Н. Справочник по статике и динамике корабля. Динамика корабля. Том 2

Подождите немного. Документ загружается.

§ б. ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ

МАССЫ

СУДНА

И ПЕРИОДОВ

СВОБОДНЫХ

КОЛЕБАНИЙ

В общем

случае

движения кинетическая энергия судна может

быть

записана

виде

где D — водоизмещение судна; g — ускорение силы тяжести; J

— момент инерции

тела относительно мгновенной оси вращения, проходящей через его центр масс,

— мгновенная угловая скорость;

(й

—

где

(£>

Юу, со

— проекции угловой скорости на оси связанной с судном системы

координат; J

, J

— моменты инерции массы относительно осей х, у, г соот-

ветственно.

Масса судна М = , тс-м"

Если

принять центр тяжести судна за начало координат, то моменты инерции

массы определяются формулами

)

< (*l

(2.11)

так

как диаметральная плоскость .судна является плоскостью симметрии. Центро-

бежный момент инерции - I

(2.12)

В формулах

(2.11)

и (2.12): /и,- — элементарная масса, определяется по статьям

нагрузки; т

{

— pjg где p

-—вес i-й статьи нагрузки; Xi, yi, г, = координаты

ее центра тяжести.

Практически

расчет

ведут

по формуле

где z

— возвышение центра тяжести судна относительно горизонтальной плоско-

сти,

проходящей через начало системы координат (в статике корабля за такую пло-

скость обычно принимают основную плоскость судна),/„ — собственный централь-

ный

момент инерции веса i-й статьи нагрузки относительно параллельной х.

Если

принять, что вес t-й статьи нагрузки равномерно распределен по площади

ее проекции со сторонами го и уо, то

, _

1 +

ixi — Pi j2 *

Для вычисления по этой формуле используется постатейный расчет нагрузки

судна. Эти вычисления весьма трудоемки, поэтому часто ограничиваются расчетом

по

приближенным формулам.

Формула Дуайера получена в предположении, что корпус судна представляет

собой сплошной прямоугольный параллелепипед шириной В и высотой 2zg, если

считать, что начало координат лежит в-основной плоскости,

Формула Шиманского выведена о предположении, что корпус судна представ-

ляет сплошной параболический цилиндр,

где В — ширина судна; Н — высота борта; а —• коэффициент полноты площади

ватерлинии; б — коэффициент общей полноты.

Эмпирическая

формула J

+ Х

= р| D/g, где р

—приведенный радиуо

инерции

судна с

учетом

присоединенной массы воды: р

= с —, где с — эмпири-

ческий

коэффициент, с =

0,80-5-0,87

для пассажирских

судов

и с = 0,81 для

грузовых

судов

в лолном

грузу.

Поскольку судно является телом, сильно вытянутым в продольном йаправле-

нии,

при вычислении момента инерции тела относительно поперечной оси можно

пренебречь г

по сравнению с х

. Практически при вычислении момента инерции J

пользуются формулой

где р, — ордината кривой весов; Д/. — длина отсека, принятая при построении

ступенчатой кривой весов; х, — абсодсса центра тяжести отсеков кривой весов от-

носительно центра тяжести судна.

Момент инерции J

может быть вычислен, исходя из строевой по шпангоутам,

f 1 DL

Я J 60 в '

где а» — площадь шпангоутов.

Первый

член правой части представляет момент инерции массы судна в пред-

положении,

что ординаты кривой нагрузки пропорциональны ординатам строевой

по

шпангоутам. Второй член

соответствует

наибольшей возможной ошибке при при-

нятии

указанного предположения. Эта формула

дает

удовлетворительный резуль-

тат, если судно имеет грузы, разнесенные к оконечностям. Если же значительные

грузы

сосредоточены^ средней части судна, то формула может дать большую по-

грешность, преувеличив момент инерции J

Для ориентировочного суждения о J

может служить формула

= 0,07 — DL»,

где а — коэффициент полноты грузовой ватерлинии.

Приближенные

формулы для присоединенных масс и присоединенных момен-

тов инерции приведены в § 6. Для ориентировочных оценок можно принять, что

Ьзз

= Dig, J1.44 =

(0,25-5-0,35)

; Х

№

= J

Приведенные зависимости позволяют получить следующие приближенные

формулы для периодов свободных колебаний:

для вертикальной качки 7*g

=•

2,5]/ Т\

для килевой качки Т$ = 2,4 /

В этих

двух

формулах принято, что коэффициент вертикальной полноты %

«= 0,75 Здесь Т — осадка судна, м;

для бортовой качки Т% = с _ц.,

где с — эмпирический коэффициент, принимающий те же значения, что и в фор-

муле

для J

+ Я^; fl — ширина судна, м; ft — начальная поперечная метацентри-

ческая высота, м.

Для вычисления периода Tg «* T^ можно пользоваться следующей прибли-

женной

формулой Ремеза, относящейся к транспортным судам е обычными обво-

дами корпуса и умеренной осадкой

= Г

- К VT,

где К —•

поправочный

коэффициент.

Значения коэффициента К

BIT 2 2,5 3 3,5 4 4,5 б

К 2,32 2,44 2,55 2,66 2,76 2,86 2,96

Для малых наклонений в пределах линейности диаграммы остойчивости можно

пользоваться следующими формулами:

где И — продольная метацентрическая высота; S — площадь ГВЛ; у «-• удельный

вес воды.

Периоды свободных бортовых и килевых колебаний судов, о

Бортовая

Килевая

качка

качке

Грузовые 7—12 4—в

Пассажирские водоизмещением, тс:

до 10 000 10—15 5—7

006—30

000

16—20

7—Ю

000—50

000

20—28

10—14

Ледоколы 6—10 3—5

Рыболовные траулеры 6—8 3—4

Авианосцы 14—1б 7—9

Крейсеры

10—16 5—8

Эсминцы

8—10 4—5

Сторожевые корабли 6—8 3—4

Малые

суда

и катера 3—5 2—3

Эти величины характеризуют плавность качки, а следовательно, и характер

вертикальных и

угловых

ускорений. Наблюдения показывают, чго в условиях

качки

судна на реальном нерегулярном волнении периоды бортовой и килевой

качки

близки к соответствующим значениям периодов их свободных колебаний

2 С. Н Благовещеноквй, А М Холодилин 33

§ 6.

ПРИСОЕДИНЕННЫЕ

МАССЫ

•

КОЭФФИЦИЕНТЫ

СОПРОТИВЛЕНИЯ

КАЧКЕ

В безграничной жидкости матрица присоединенных масс содержит 36 членов

п Кг

Ki Кг

Кг

К,

к*

в4

Ли ЛЩ

25 26

4в

5в

в5

Ов

В гидромеханике установлено,что при нестационарном движении в безграничной

жидкости справедливо свойство парности К

т1

= Х

1т

, т. е. матрица присоединенных

масс симметрична относительно главной диагонали. Строго говоря, при качке судна

присоединенные

массы зависят не только от формы тела, но и от частоты и амплитуды

колебаний,

поэтому свойство парности уже не имеет места. Однако во многих зада-

чах качки все же считают применимым свойство парности.

В гидромеханике понятия присоединенных масс обобщают на случаи, когда

тело движется в ограниченной жидкости, а также при наличии свободной взволно-

ванной

поверхности. Размерность присоединенной массы (статического момента,

момента инерции присоединенной массы) приведена ^.на С. 29.

Можно

показать, что для судна, симметричного относительно диаметральной

плоскости xGz, число присоединенных масс сокращается до 12

= л

= Я

= А

"•

В этом

случае

матрица присоединенных масс имеет вид

Кг

К,

Кг

К*

^•33

^63

К,

^44

Кь

^•26

Кв

Лея

учетом

свойства парности здесь А,

= Я,

Я1

; Я

= Я

в1

; Я

= K

; К»

^e*t

^35 ~L ^53! Кя ~ Kf

У судна, симметричного относительно

двух

плоскостей (диаметральной плоско-

сти и мидель-шпангоута), остается только восемь присоединенных масс, так как

*13 = V = А-35 = ^63 = ^4в = V = *-2в = Кг = °- Д

дя тела

- симметричного

относительно

трех

плоскостей (трехосный эллипсоид), остается только шесть при-

соединенных коэффициентов, расположенных на главной оси матрицы к^; Кг'>

Кь>

^44;

К&>

Кв-

В качке корабля присоединенные массы

зачастую

относят к полюсу 0, за ко-

торый принимают точку пересечения плоскости ватерлинии, диаметральной пло-

скости и мидель-шпангоута. Обозначим присоединенные массы, отнесенные к этому

полюсу, №

, а отнесенные к системе осей

Gxyz

—Я .. Формулы, связывающие эти

величины,

выведены впервые В. М. Лаврентьевым

И —

1Ь

22)

ЗЗ.

1 — 1

А44 —

*44

i =

55 '

_2jO ,

„2,0

•

1°

jj> •

3 = 0;

*(Лзз;

где дго, го — координаты G относительно 0.

По

аналогии с присоединенными массами рассмотрим коэффициенты пропор-

циональности при силах сопротивления. Полная матрица имеет вид

"35

"65

Пренебрегая влиянием скорости на коэффициенты демпфирования и полагая,

как

и для присоединенных масс, справедливым свойство парности b

= b

, полу-

чим расчетную матрицу для судна, симметрияпэго относительно диаметральной

плоскости,

*31

0 '

*42

Ът

&53

*24

*44

*.4

ъъ

*4в

Поскольку оси координат располагают параллельно главным направлениям

движения, то Х

1г

= Я

= 0, таким образом вводится дополнительное упро-

щение

= я

= о и г>

= &

= о.

Расчет присоединенных масс может быть выполнен теоретическим путем или на

основании

анализа экспериментального материала по испытанию моделей

судов

опытовых бассейнах. Для упрощенных зависимостей используют эмпирические

формулы и номограммы.

Бортовая качка. Наибольший интерес представляют коэффициенты А,

и Ь

По

заданию

ЦНИИМФ

в опытовом бассейне ЛКИ были проведены серийные испыта-

ния

моделей судов. Обводы корпусов первой-серии были близки к обводам извест-

ной

60-й серии, которые весьма характерны для современных транспортных (грузовых

пассажирских) морских судов. Испытания охватывали достаточно широкий диапа-

зон

изменения относительной метацентрической высоты 0,02 ^ hi В ^ 0,15. Ре-

зультаты

испытания представлены в виде номограмм для определения присоеди-

ненного

момента инерции (рис. 2.3) и коэффициента демпфирования (рис. 2.4) транс-

портных судов.

Присоединенный

момент инерции определяется формулой

0,314

"•44'

где У

л — момент инерции подводной части эллипсоида, имеющего те же главные

размерения и коэффициент общей полноты, что и данное судно (модель),

коэффи-

циент

Я,

ЭЛ

снимают с номограммы (рис. 2.3) Там же штрих-пунктиром указан

ключ пользования номограммой при BIT = 2,8, б = 0,70; а = 0,78.

• 35

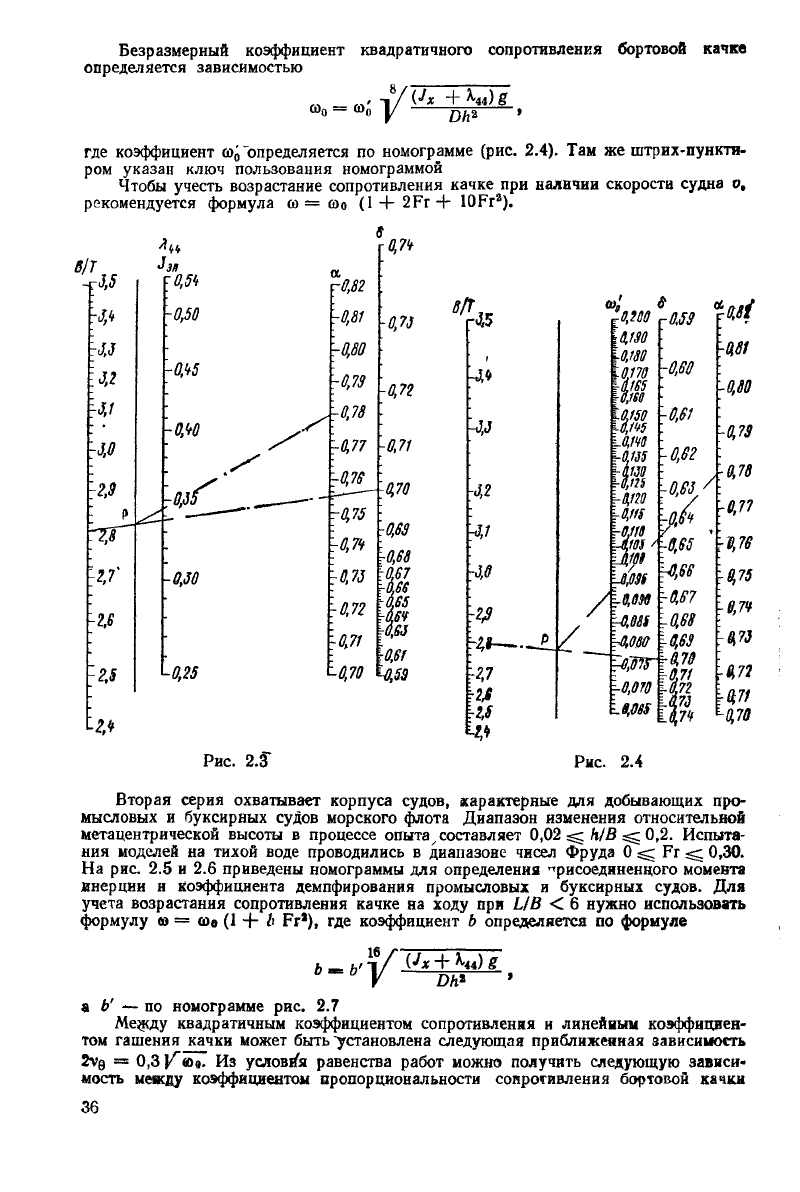
Безразмерный

коэффициент квадратичного сопротивления бортовой качке

определяется зависимостью

«о =

о у

Dh*

где коэффициент

ш^

"определяется по номограмме (рис. 2.4). Там же штрих-пункти-

ром указан ключ пользования номограммой

Чтобы

учесть

возрастание сопротивления качке при наличии скорости судна о,

рекомендуется формула со = а>о (1+ 2Fr + 10Fr

Рис.

2.3*

Рис.

2.4

Вторая серия охватывает корпуса судов, характерные для добывающих про-

мысловых и буксирных

судов

морского флота Диапазон изменения относительной

метацентрической высоты в процессе опыта ^составляет 0,02 «g hi В sg 0,2. Испыта-

ния

моделей на тихой воде проводились в диапазоне чисел Фруда 0 ^ Fr ^ 0,30.

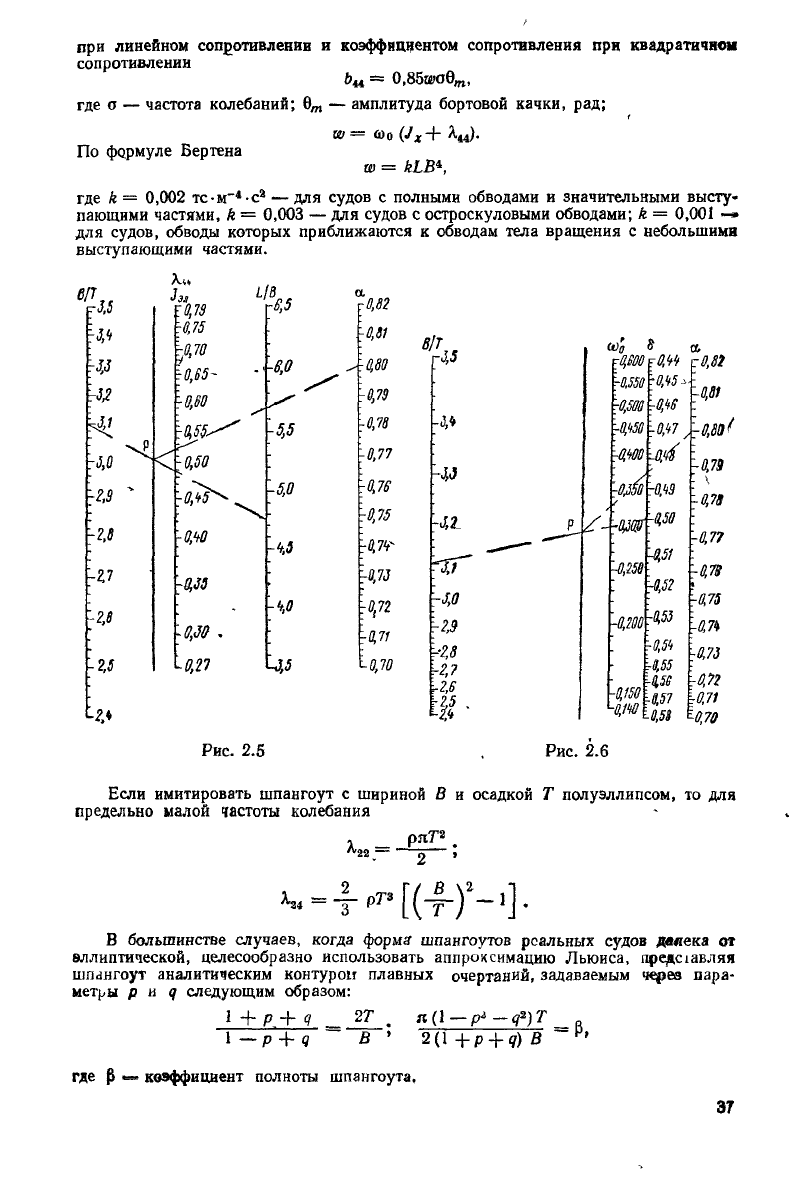
На

рис 2.5 и 2.6 приведены номограммы для определения присоединенного момента

инерции

и коэффициента демпфирования промысловых и буксирных судов. Для

учета

возрастания сопротивления качке на

ходу

при LIB < 6 нужно использовать

формулу ее = а>е (1 + b Fr

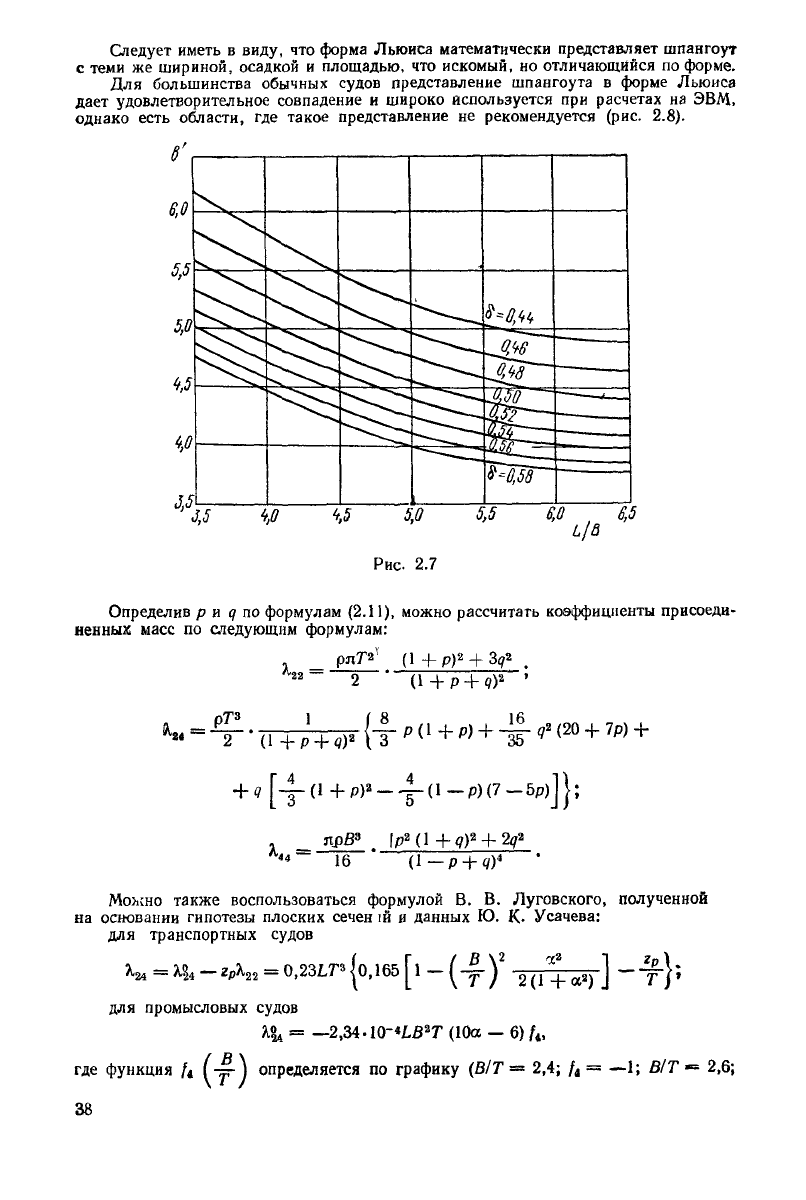
), где коэффициент b определяется по формуле

Ь'

Dh*

а Ъ' — по номограмме рис. 2.7

Между квадратичным коэффициентом сопротивления и линейным коэффициен-

том гашения _качки может быть "установлена следующая приближеяная зависииость

2vg = 0,3

\Г<Ьъ.

Из условия равенства работ можно получить

следующую

зависи-

мость

между

коэффициентом пропорциональности сопротивления бортовой качки

при

линейном сопротивлении и коэффициентом сопротивления при квадратичной

сопротивлении

По

формуле Бертена

где о — частота колебаний; 6

— амплитуда бортовой качки, рад;

— Шо (•/*+ ^44).

w =

kLB*,

где k =

0,002

тс-м"*-с

— для

судов

с полными обводами и значительными

высту-

пающими частями, k =

0,003

— для

судов

с остроскуловыми обводами; k = 0,001 -•

для судов, обводы которых приближаются к обводам тела вращения с небольшими

выступающими частями.

-0,д2

-0,11

:**

J,0

-2,9

V-2,8

•-2,1

Us.

ш'о » а

-0,500

-ом

•0,45

'4,259

•0,150

п,№\

-.ОД

\0fil

0,50

4,51

-0,52

-0,200

-W

-0,5i

4,55

457

-0.lt

0,5$

-0,77

-0,7В

0,15

0,70

Рис.

2.5

Рис.

2.6

Если имитировать шпангоут с шириной В и осадкой Т полуэллипсом, то для

предельно малой частоты колебания

В большинстве случаев, когда формз шпангоутов реальных

судов

далека от

вллиптической, целесообразно использовать аппроксимацию Льюиса, предоавляя

шпангоут аналитическим контуром плавных очертаний, задаваемым через пара-

метры р и q следующим образом:

2Г яП — Р*-

1+Р.+

-p + q

2(1

где

коэффициент

полноты шпангоута,

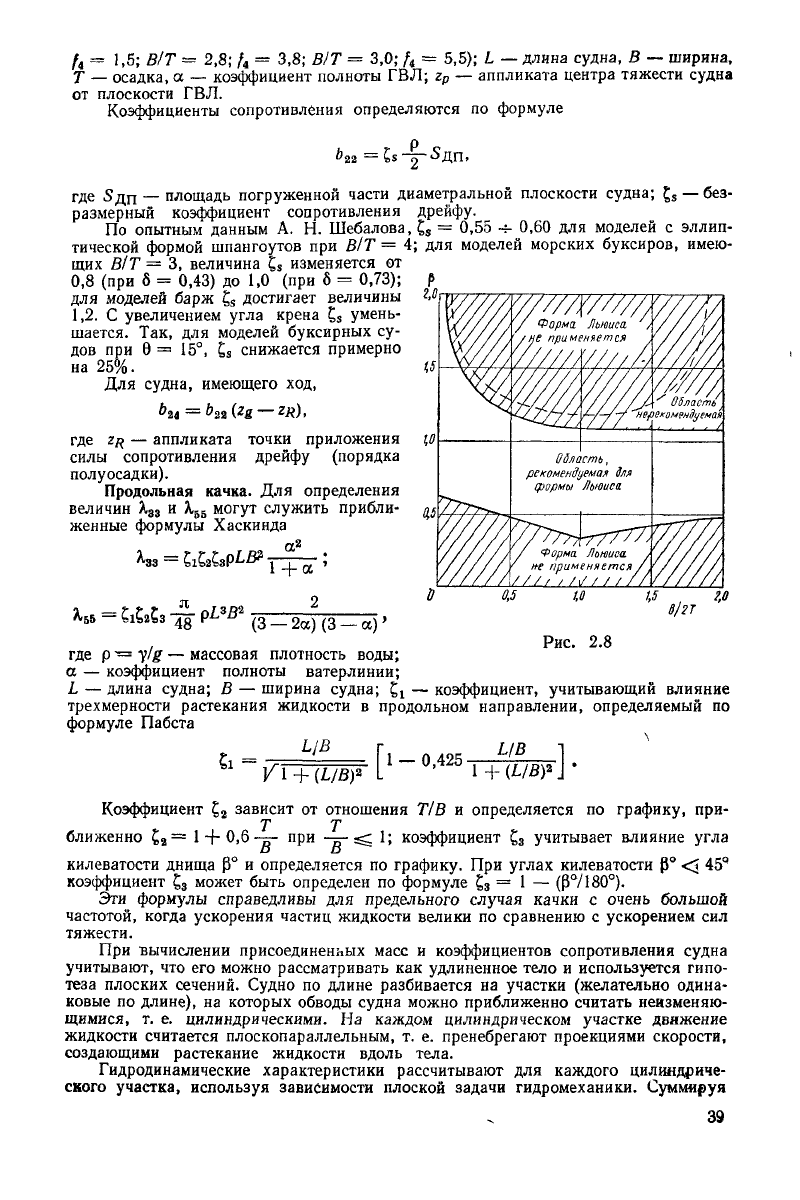
Следует иметь в виду, что форма Льюиса математически представляет шпангоут

теми же шириной, осадкой и площадью, что искомый, но отличающийся по форме.

Для большинства обычных судов представление шпангоута в форме Льюиса

дает

удовлетворительное совпадение и широко используется при расчетах на ЭВМ,

однако

есть области, где такое представление не рекомендуется (рис. 2.8).

5,0

Рис.

2.7

5,5 ~ 6,0 6,5

L/B

Определив р и q по формулам (2.11), можно рассчитать коэффициенты присоеди-

ненных

масс по следующим формулам:

—

Молено

также воспользоваться формулой В. В. Луговского, полученной

на

основании гипотезы плоских сечен ш и данных Ю. К- Усачева:

для транспортных судов

*Ь -«P*M =

O,23Lr»|o,165

[l - [-~

+о»)

для промысловых судов

Х^ =

_2,34.10-«LB

(10а — 6) /«,

где функция ft (

-=•)

определяется по графику (В/Т

2,4; /

= —1; В/Т «= 2,6;

= 1,5; В/Т = 2,8; /

= 3,8; BIT = 3,0; f

= 5,5); L — длина судна, В — ширина,

— осадка, а — коэффициент полноты ГВЛ; г

— аппликата центра тяжести судна

от плоскости ГВЛ.

Коэффициенты

сопротивления определяются по формуле

имею-

где

Sflji

— площадь погруженной части диаметральной плоскости судна; £

— без-

размерный коэффициент сопротивления дрейфу.

По

опытным данным А. Н. Шебалова, £

= 0,55 -=- 0,60 для моделей с эллип-

тической формой шпангоутов при В/Т = 4; для моделей морских буксиров

щих В/Т = 3, величина ts изменяется от

0,8 (при б = 0,43) до 1,0 (при б =

0,73);

для моделей барж £

достигает величины

1,2. С увеличением

угла

крена £

умень-

шается. Так, для моделей буксирных су-

дов при Э = 15

, £

снижается примерно

на

25%.

Для судна, имеющего ход,

где z# — аппликата точки приложения

силы сопротивления дрейфу (порядка

полуосадки).

Продольная

качка. Для определения

величин Х

и Х

ъь

могут

служить прибли-

женные формулы Хаскинда

Область,

рекомендуемая

для

формы

Льюиса.

, Рис. 2.8

где р

•=

y/g — массовая плотность воды;

а — коэффициент полноты ватерлинии;

— длина судна; В — ширина судна; £i — коэффициент, учитывающий влияние

трехмерности растекания жидкости в продольном направлении, определяемый по

формуле Пабста

LIB

V\+{LIB)*

Коэффициент

зависит от отношения Т/В и определяется по графику, при-

ближенно £

= 1 + 0,6-=- при -5-=g 1; коэффициент £

учитывает влияние

угла

и D

килеватости днища (5° и определяется по графику. При

углах

килеватости Р° <j 45"

коэффициент

может быть определен по формуле £

= 1 —

((57180°).

Эти формулы справедливы для предельного случая качки с очень большой

частотой, когда ускорения частиц жидкости велики по сравнению с ускорением сил

тяжести.

При

вычислении присоединенных масс и коэффициентов сопротивления судна

учитывают, что его можно рассматривать как удлиненное тело и используется гипо-

теза плоских сечений. Судно по длине разбивается на участки (желательно одина-

ковые по длине), на которых обводы судна можно приближенно считать неизменяю-

щимися,

т. е. цилиндрическими. На каждом цилиндрическом участке движение

жидкости считается плоскопараллельным, т. е. пренебрегают проекциями скорости,

создающими растекание жидкости вдоль тела.

Гидродинамические характеристики рассчитывают для каждого цилиндриче-

ского участка, используя зависимости плоской задачи гидромеханики. Суммируя

вти величины, получают гидродинамические характеристики судна в целом. Обычно

судно разбивают на 20 теоретических шпаций и расчет

ведут

по 20 или 10 сече-

ниям.

В последнем

случае

за расчетные сечения принимают нечетные шпангоуты 1,

3, 5, . . ., 19.

Гидродинамические характеристики плоских контуров рассчитывают теорети-

чески или проводят экспериментальные замеры на цилиндрических моделях в опы-

товых бассейнах Наибольшей популярностью пользуются результаты, полученные

А. 3. Салькаевым, Портером, Тасаи.

Метод Салькаева.

Автор

теоретически определил гидродинамические силы,

действующие на пересекающий свободную поверхность плоский контур произволь-

ной

формы. При решении задачи введено допущение, что плавающий контур все

время занимает положение, совпадающее с положением равновесия на тихой воде,

но

распределение скоростей и ускорений в каждый момент времени

соответствует

их значениям для. колеблющегося контура. Частота колебания контура принимается

равной

частоте набегающих на него волн. Решение получено на базе результатов

М. Д. Хаскинда.

А. 3. Салькаев вычислил все величины и построил графики. Поскольку гндро-

динамияееки

задача решается в идеальной жидкости, демпфирующие составляющие

учитывают точько волновые компоненты.

Графики

приведены к безразмерному

виду.

Так, для вертикальной качки

,р°"

гдеА,

(х) — присоединенная масса, приходящаяся на единицу длины судна; 6

(х)—

коэффициент

линейного сопротивления, приходящегося на единицу длины судна;

р — массовая плотность воды; а — частота волны; 2а — ширина Контура по ГВЛ.

Кроме

этого, на графиках использованы обозначения: Р — коэффициент полноты

шпангоута, Т — осадка, k = aVg — волновое число.

В дальнейшем для упрощения опустим скобки у присоединенных масс и

коэф-

фициентов

демпфирования как в формулах, так и на графиках.

Тогда коэффициент демпфирования и присоединенная масса

могут

быть вычис-

лены как интегралы

{*)

Для килевой качки коэффициенты демпфирования и момент инерции присое-

диненной

массы

могут

быть вычислены посредством интегралов

*8В

(*)

> ^»5

**^68

L L

ъъ

» J

хЬ

зъ

(х)

dx;

= j х\

аз

(x)

dx.

На

рис.

2.9—2.14

приведены графики А. 3. Салькаева для 6

на

с 2.15—

2.20 — для 6

, на рис.

2.21—2.26

— для "Х

2г

, на рис.

2.27—2.32

— для А,

г4

. на

рис.

2.33—2.38

—для Ь~

, на рис

2.39—2.44

— для 1

, на рис.

2.45—2.50—для

аа

на рис.

2.51—2.56

— для Х

Каждйй рисунок

соответствует

определенному значению коэффициента полноты

шпангоута р. Промежуточные значения интерполируются.

Пример

расчета величин по графикам Салькаева приведен в § 16.

Метод Портера. Портер вычислил присоединенную массу, коэффициент демп-

фирования

и отношение высоты волны к вертикальным колебаниям цилиндров,

имеющих контуры,

судовых

шпангоутов.

Всего

рассмотрено 62 контура, которые

разбиты на различные группы в зависимости от площади шпангоута, отношения осадки