Благовещенский С.Н., Холодилин А.Н. Справочник по статике и динамике корабля. Динамика корабля. Том 2

Подождите немного. Документ загружается.

Для^«61/1-4

имеем

1; Г (1/2) = ]Ая; Г(0)=-оо.

Остальные значения гамма-функции приведены в приложении 2.

Спектры

волнения 12-й МКОБ и 2-го

МКПС

приведены в табл. 1.6 и 1.7 соот-

ветственно.

При

вычислении спектра 2-го

МКПС

принято

3,92

0,383/i

30/

V+

143

для а>0пр:

«ар-

(а) = 0 для а <g а

пр

O,1125/z

30/o

+2,25

глава

ОБЩИЕ

УРАВНЕНИЯ

НАЧКИ СУДНА

§ 4.

СИСТЕМЫ

КООРДИНАТ. ОБЩИЕ

УРАВНЕНИЯ

Движущееся на взволнованной поверхности моря судно

можно

рассматривать

как

абсолютно твердое тело с шестью степенями свободы. При расчетах качки судна

применяют три системы прямоугольных координат: неподвижную и две подвижные.

Неподвижная

система координат Ох^т]^! имеет плоскость 0

т]

, совпадающую

с невозмущенной поверхностью жидкости, а ось 0

направлена вертикально вниз.

Первая

подвижная система координат 0£г)£ имеет плоскость

Ogrj,

совпадающую

с плоскостью O^jT)!, а ось 0£ направлена вертикально вниз, начало координат О

движется с постоянной скоростью v, равной скорости движения судна, ось 0\ сов-

падает с направлением этой скорости и составляет

угол

8 с осью 0^. Вторая по-

движная система координат жестко связана с судном. В Зависимости от решаемых

задач начало этой системы

берут

либо в точке пересечения диаметральной

ПЛОСКОСТИ

хОг, плоскости ГВЛ (хОу) и плоскости мидель-шпангоута (уОг),

тогда

система

Охуг;

либо в центре тяжести судна G,

тогда

Gxyz;

либо так, что ось Ог проходит через-

центр тяжести и направлена вниз. Обе подвижные системы должны совпадать в по-

ложении равновесия судна в жидкости. Поэтому в случае, когда начало координат

принимается

в центре тяжести судна, вводят еще одну систему координат, либо

предполагают, что центр тяжести лежит в плоскости ГВЛ.

Переход от неподвижной к первой подвижной системе координат осуществляете»

по

формулам

Si = (S + of) cos e — т) sin ej

% =

Г\

COS 8 + (g

•+

Of) Sin 8J

где»—средняя величина скорости прямолинейного поступательного движения судна

t — время, прошедшее о момента совпадения точки O

с точкой О, в —

угол

между

осями

0^! и 01.

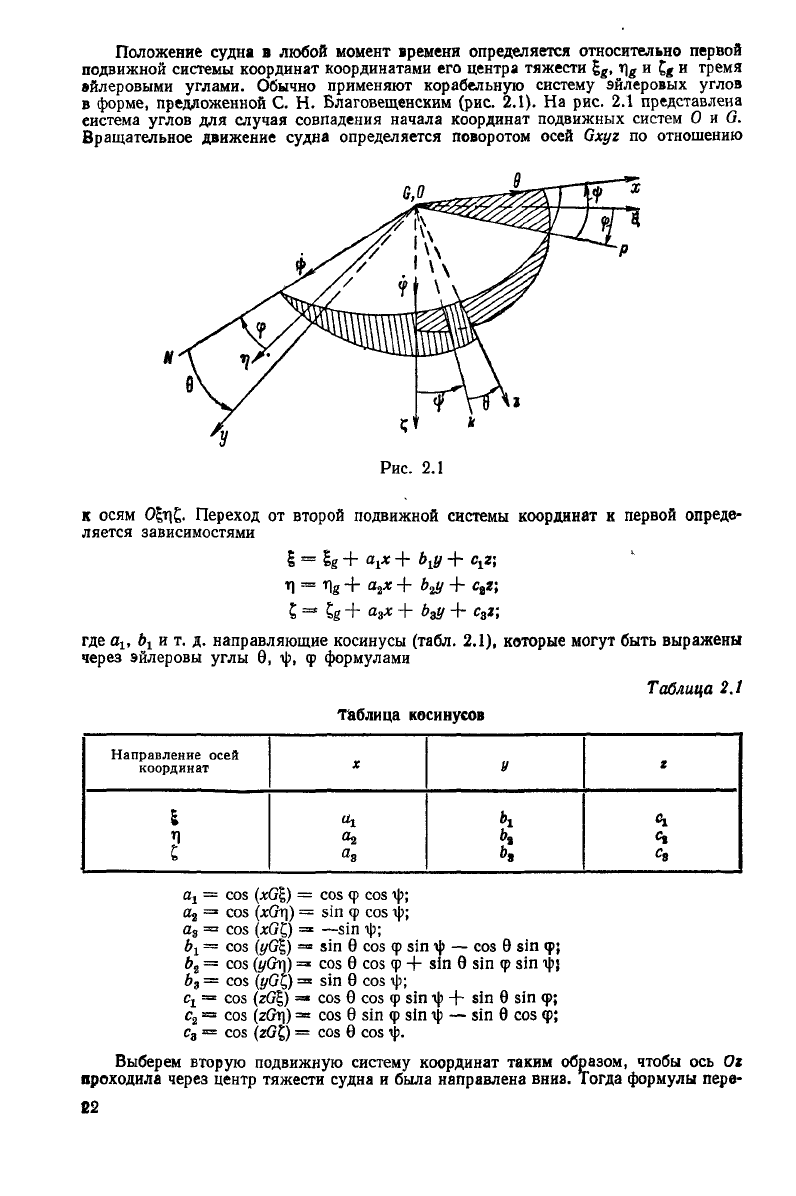
Положение судна в любой момент времени определяется относительно первой

подвижной системы координат координатами его центра тяжести £

, r\

и tg и тремя

вйлеровыми углами. Обычно применяют корабельную систему эйлеровых

углов

форме, предложенной С. Н. Благовещенским (рис. 2.1). На рис. 2.1 представлена

система

углов

для случая совпадения начала координат подвижных систем О и G.

Вращательное движение судна определяется поворотом осей

Gxt/г

по отношению

6,0

Рис.

2.1

осям О£т)£. Переход от второй подвижной системы координат к первой опреде-

ляется зависимостями

l—tg+a

y + C&

Л = % + V + Ь$+ с

г\

£ =» l

+ а

х +

ЬзУ

+ с

г;

где a

и т. д. направляющие косинусы (табл. 2.1), которые

могут

быть выражены

через эйлеровы

углы

0, г|), <р формулами

Таблица

2.1

Таблица косинусов

Направление

осей

координат

ь,

= cos (xG^) = cos

cos i|);

= cos

(xGrf)

= sin ф cos ij);

= cos (xGQ

=•

—sin

\p;

= cos

(yGB,)

=« sin 9 cos <p sin i|) — cos 0 sin q>;

= cos (уОц) = cos 6 cos ф 4- sin 9 sin <p sin ф)

= cos (yQt) = sin 8 cos -ф;

= cos (zG\) =* cos 0 cos ф sin a|) + sin 9 sin ф;

= cos

(ZGTJ)

== cos 0 sin ф sin ij) — sin 9 cos ф;

= cos (zGJ) = cos 9 cos ij).

Выберем

вторую

подвижную систему координат таким образом, чтобы ось Ог

проходила через центр тяжести судна и была направлена вниа. Тогда формулы пере-

кода для подвижных систем координат имеют вид

= |

+ х cos ф cos i|>

•+•

у (sin 6 cos ф sin ty — cos 9 sin ф) + (г — г

) X

X (cos 0 cos ф sin i|) + sin 9 sin ф);

4 = T)g + x sin ф cos г|э + у (cos 9 cos ф + sin 0 sin ф sin i|>) + (z — z

) X

X (cos 9 sin ф sin \p — sin 9 cos ф); (2.Ц

£ = £

— * sin v|> + у sin 9 cos ф + (z — z

) cos 0 cos i|);

* = (i — Sg) cos ф cos г|) + (Л — Tig) sin ф cos

я|>

— (£ — £

) sin г|>;

0 = (S — eg) (sin 9 cos ф sin ty — cos 0 sin ф) + On — 1g) (cos 0 cos ф +

sin 0 sin ф sin i])) + (£ — £g) sin 0 cos t|); (2.2>

г = г

+ (| — £g) (cos 0 cos ф sin г|) + sin 0 sin ф) +

(т) — T)g) (cos 0 sin ф sin if — sin 0 cos ф) + (£ — £g) cos 9 cos i|)),

где |g, Ti

, Jg — координаты центра тяжести судна в первой подвижной системе

координат, г

— аппликата центра тяжести во второй подвижной системе (г

= О

тогда,

когда центр тяжести расположен в плоскости ватерлинии равновесия).

При

проведении практических расчетов обычно применяют разложение синусов^

косинусов эйлеровых

углов

в ряды

ш*

тг

случае

наклонений на малые

углы

синусы заменяют их значениями, а коси-

нусы принимают равными 1. Это первое приближение, широко применяемое при

построении линейной теории качки. Значения направляющих косинусов для пер-

вого приближения приведены в табл. 2.2,

Таблица

2.2

Таблица косинусов (первое приближение)

Направление

осей

координат

-ф

— 9

учетом

этих зависимостей связь координат для произвольной точки А судна

примет вид

+ х — фу + г|>г;

•Hg

+ Ф* + У — 6*;

(2.3>

Во втором приближении ограничимся

учетом

величин до второго порядка ма-

лости включительно. Направляющие косинусы для второго приближения приведены

табл. 2.3. Тогда для произвольной точки А судна связь координат определится

зависимостью

Таблица

2.8

Таблица кбсинусов (второе приближение)

Направление

осей

координат

ф2

— 1

2 2~

—

в-

ф2

<.+("--*-?•)•

•('-•?-¥-)*

(2.4)

Если принять начало второй подвижной системы координат за полюс, то ско-

рость в произвольной точке А судна определится зависимостью

где Vo — вектор скорости полюса, со — вектор мгновенной угловой скорости вра-

щения

судна

— радиус-вектор точки А. \

Проекции

векторного равенства на

оси первой подвижной системы координат

имеют вид

- У -

- С,);

-• _

где

«-,<»„

и и, — проекции вектора <в на соответствующие оси координат, ©ни

могу»

быть выражены через

угловые

скорости, соответствующие выбранным эйлеровым

углам

результате

можно получить следующие выражения;

первом приближении

во втором приближении

\А

* h —

(ФФ

<И>)

—

+ ф* —

фф)

у + (—ё +

ф1|)

(2.6)

(2.61

•4

Как

видно из рис. 2.1,

углы

9, gON и zOk находятся в одной плоскости, к ко-

торой перпендикулярна ось Ох, поэтому вектор 6

следует

направить по оси Ох.

Линия

узлов ON, образованная пересечением координатных плоскостей %Оц и уОг,

перпендикулярна плоскости t,Ox в которой измеряются

углы

1);, рОх и £О£, поэтому

вектор ф направлен по линии ON.

Угол

ф лежит в плоскости |Оп (.также

углы

ЪРр

NOr\), а вектор ф направлен по оси 0£, перпендикулярной этой плоскости. Оче-

видно,

что проекции вектора угловой скорости а, <в., <в и о. направлены соответ-

ственно по осям 01, 0г\ и О£. Согласно рис. 2.1 имеем

©j

= 9 cos г|) cos ф — ф sin\q>;

<a,l

= 4 cos ф — б sin i|) cos ф|

= <р — 9 sin ф.

Фтсюда:

Первое приближение Второе приближение

Аналогично можно получить проекции вектора угловой скороота со на оси

связанной

с судном системы координат

Охдг

(й

9— ф sin ф;

а>

= ij) cos 9 + ф cos t|) sin 8j

<о

= ф cos 9 cos

-ф

— ф sin в.

Соответственно имеем:

Первое приближение Второе приближение

= ф = cog. со

== ф

—•

ф9.

Векторное выражение для ускорения произвольной точки А судна имеет вид

где а)д

*->>

вектор ускорения точки, е «• вектор

углового

ускорения.

Проекции

вектора ускорения на оси координат 0£т]£

дадут

следующие выраже-

ния:

1А

= Ig

Первое

приближение

2вф)

в?

Фв

2в<р)

г;

fc»

=l"

-^x +

—

("ев

в»

фф

)

г.

Учитывая, что направление координатных осей связанной с судном системы

•координат меняется, и это затрудняет определение проекции ускорений на коорди-

натную ось как производную по времени от проекции скорости и ускорения точки,

имеем

VAX = Vgx — (O

y +

<Dj,ZJ

Улу = V

— ш*г + е>

х;

VAZ

= Vgz —

v>yx

+ <o

Здесь проекции скорости центра тяжести и проекции вектора мгновенной

утло-

«вой

скорости определяются известными формулами

= Ш|С, + (О^ +

Сй£С

Тогда для первого приближения

VAX

= ig + m

—

4>Ce

— W +

V%, = i]g — ф1в + e?

— Вг +

Если проекции скоростей центра тяжести судна малы, то вторые и третьи члены

выражений

будут

малыми второго порядка малости и

могут

быть исключены в пер-

.вом приближении.

Для второго приближения

Vte= Is ^

= hg ~

(в

V*)

г +

(Ф

х\

•56

Проекции

ускорений (направляющие косинусы не дифференцируются) имеют

вид:

в первом приближении

во втором приближении

WAx

= Ig + ФЛй - *Ь ~ 4"

(ф

_ (ip _ e$ - 2&ф) у + (ф + 6<p + 29ф) *;

— (G — фчр — 2iH>) г + (Ф — фв) х;

—g-(в»-

— (* +

фв)

* +

(**—ФЧ>)

У-

Эти формулы

дают

проекции скоростей и ускорений фиксированной точки-

судна. В первом приближении они линейные функции, а во втором приближении

образуют многочлены второго порядка относительно углов,

угловых

скоростей

угловых

ускорений судна при качке.

Линейную систему уравнений движения судна, имеющего шесть степеней сво-

боды, в общем виде можно записать следующим образом:

2lig

(2.9>

t +

r\g

iig

+ c

+ *„& +

+ ф ф i

•где

Ri, /?

, /?j — проекции вектора внешних сил, Afg, Л?_, М» —' проекции

век»

тора момента внешних сил.

Неизвестными

в этой системе являются координаты центра тяжести g

, t)

, £g

три эйлерова

угла

9, if, q>.

В первом приближении можно считать эйлеровы

углы

в, •ф, <р совпадающими

с углами крена, дифферента и рыскания, тогда линейные и угловые колебания судна

именуются в соответствии с терминологией, приведенной в табл. 2.4. О характере

колебаний

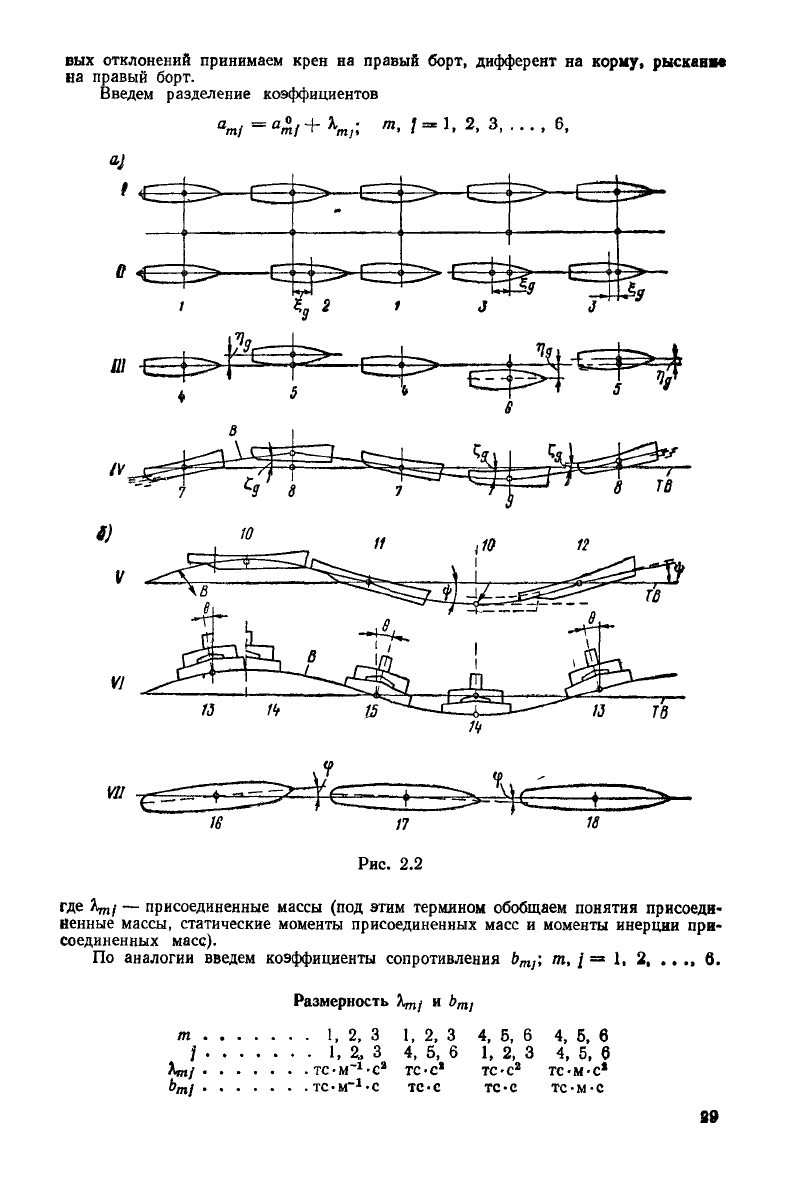
судна можно судить по схеме, приведенной на рис. 2.2 (рис. 2.2, а — ли-

нейные,

рис. 2.2, б — угловые). На рисунке приняты обозначения: / — судно

движется с постоянной скоростью прямолинейным курсом; // — горизонтально-

продольные колебания; /// — горизонтально-поперечные колебания; IV — верти-

кальная

качка; V — килевая качка; VI — бортовая качка; VII — рыскание; 1 —>

горизонтально-продольные отклонения равны нулю; 2 — колебания вперед от сред-

него положения; 3— колебания назад от среднего положения; 4 — дрейф равен

нулю; 5 — дрейф на левый борт; в — дрейф на правый борт; 7 — вертикальные

отклонения

равны нулю; 8 — всплытие; 9 — погружение; 10 — на ровный киль;

// — дифферент на нос; 12 — дифферент на корму; 13 —

угол

крена на правый

•Ч5орт; 14 — прямое положение (угол крена равен нулю); 15 —

угол

крена на левый

-борт; 16 —

угол

рыскания на левый борт; 17

—.угол

рыскания на правый борт;

— среднее положение (судно ла заданном курсе); В — поверхность волны; ТВ —

поверхность тихой воды.

Таблица 2.4

Термины,

обозначающие линейные и угловые перемещения вдоль осей, которые

проходят через центр тяжести судна

Ось

Ог

по-русски

Термины

по-английски

по-немецки

по-фран-

цузски

Линейные

перемещения

вдоль

осей

Горизонтально-

продольные коле-

Горизонтально-

поперечные колеба-

ния

Вертикальная

качка

Бортовая качка

Килевая

качка

Рыскание

Surging

(to

surge)

waying

(to

sway)

Heaving

(to

heave)

—

Die

Tauch-

schwingung

(tauehen)

Вращение

вокруг

осей

Rolling

(to

roll)

Pitching

(to

pitch)

Kawing

(to

yaw)

Die

Roll-

schwingung

(rollen)

Die

Stampf-

bewegung

(stampfen)

Die

Qier-

schwingung

(gieren)

—

(diporter)

Le pilon-

nage •

(pilonner)

Le roulis

(rouler)

Le tangage

(tanguer)

L'embarde-

ment

(embarder)

по-голланд-

ски

(schrikken)

(versetten)

(dampen)

(schingeren)

(stampen)

(gieren)

За

положительные линейные перемещения принимаем перемещения вдоль

положительных направлений осей Ох, Оу, Ог; за положительные направления угло-

вых отклонений принимаем крен

на

правый борт, дифферент

на кориу, рысканм

на

правый борт.

Введем

разделение коэффициентов

mi=

ml+Kn

m. f-1. 2, 3 6,

где %mf

—

присоединенные массы

(под

этим термином обобщаем понятия присоеди-

ненные массы, статические моменты присоединенных масс

моменты инерции

при-

соединенных масс).

По

аналогии

введем

коэффициенты сопротивления

т1

; т, [ = 1, 2 в.

Размерность

Xmj и Ь

1, 2, 3

Кп] тс-м^-с

bml

тс-м^-с

'mi

2, 3 4, 5, 6 4, б, 6

5, 6 1, 2, 3 4, 5, 6

тс-с* тс-с

тс-м-с*

тс-с

тс-м-с

Используя результаты вычисления инерционных составляющих, проведенного

С. Н. Благовещенским, н применяя принцип . суперпозиции, можно записать сле-

дующую

упрощенную систему уравнений:

Кд в +

6446

+ яле _

^ + Af

; .

(2.10)

где /?, <—

тяга,

»— момент тяги, о — скорость судна|

^ =

/?,,,

+ R^r + Я^у;

Здесь индекс «0» определяет главную часть возмущающих сил и моментов

определяемых по гипотезе А. Н. Крылова «качающееся судно не влияет»яа гидроди-

намическое поле давлений окружающей судно взволнованной жидкости; дополни-

тельные возмущающие силы и моменты, обусловленные дифрагированным волновым

движением, отмечены индексом «г», а силы и моменты, создаваемые успокоителем

качки,

индексом «у».

Кроме

этого, приняты следующие обозначения: 7 — удельная плотность воды,

— площадь ГВЛ, / — абсцисса центра тяжести площади ватерлинии в системе

координат

Gxyz,

h — поперечная метацентрическая высота, Н — продольная мета-

центрическая высота, D — водоизмещение судна, g — ускорение силы тяжести;

Jx> Jy Jz — моменты инерции массы относительно осей х, у, г соответственно,

— центробежный момент инерции относительно оси Оу.

Вычисление главной части возмущающих сил и моментов, а также дополнитель-

ных гидродинамических сил и моментов в общем

случае

движения судна приводят

громоздким выражениям, поэтому в современных расчетах качки при решении

практических инженерных задач обычно ограничиваются рассмотрением частных

видов качки судна, например случаем качки судна, расположенного лагом к вол-

нению

(боковая качка) или случаем качки судна, расположенного вразрез волне

(продольная качка).