Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena

Подождите немного. Документ загружается.

s20.4 Boundary Layer Mass Transport with Complex Interfacial Motion

637

(b)

To get the surface-averaged value of the mass flux, we integrate the above expression

over all

and

and divide by the sphere surface:

sin

8 d8

In going from the second to the third line, we made the change of variable cos

and

to get the fourth line, we factored out

from the numerator and denominator. Equa-

tion 20.3-28 was cited in

Eq.

18.5-20 in connection with absorption from gas bubbles.' This

equation is referred to again in Chapter 22 in connection with the subject of mass transfer

coefficients.

520.4

BOUNDARY LAYER MASS TRANSPORT WITH

COMPLEX INTERFACIAL

Time-dependent interfacial motions and turbulence are common in fluid-fluid transfer

operations. Boundary layer theory gives useful insight and asymptotic relations for these

systems, utilizing the thinness of the concentration boundary layers for small

9,,

(as in

liquids) or for flows with frequent boundary layer separation (as at rippling or oscillating

interfaces). Mass transfer with simple interfacial motions has been discussed in 918.5 for a

laminar falling film and a circulating bubble, and

Example 20.1-4 for a uniformly ex-

panding interface. Here we consider mass transfer with more general interfacial motions.

Consider the time-dependent transport of species

between two fluid phases, with

initially uniform but different compositions. We start with the binary continuity equa-

tion for constant p and

9,,

(Eq.

19.1-16,

divided by p):

We now want to reduce this to boundary layer form for small %,,, and then present so-

lutions for various forced-convection problems with controlling resistance in one phase.

We use the following boundary layer approximations:

(i)

that the diffusive mass flux is collinear with the unit vector

normal to the

nearest interfacial element. (This approximation is used throughout the bound-

ary layer sections of this book. Higher-order approximations: not treated here,

are appropriate for describing boundary layer diffusion near edges, wakes, and

separation loci.)

Levich,

Physicochemical Hydrodynamics,

Prentice-Hall, Englewood Cliffs, N.J.

(1962),

408,

Eq.

72.9.

Angelo, E.

Lightfoot,

and

D. W.

Howard,

AKhE Journal,

12,751-760 (1966).

Stewart,

Angelo,

and

Lightfoot,

NChE Journal,

16,771-786 (1970).

Stewart,

AKhE

Journal,

33,2008-2016 (1987); 34,1030 (1988).

Newman,

Electroanal. Chem. and Interfacial Electrochem.,

6,187-352 (1973).

638

Chapter

Concentration Distributions with More Than One Independent Variable

(ii) that the tangential fluid velocity relative to the interface is negligible within the

concentration boundary layer. (This approximation is satisfactory for

fluid-fluid systems free of surfactants, when the interfacial drag is not too

large.)

(iii) that the concentration boundary layer along each interface is thin relative to the

local radii of interfacial curvature.

(iv)

that the concentration boundary layers on nonadjacent interfacial elements do

not overlap.

Each of these approximations is asymptotically valid for small

9,,

in nonrecirculating

flows with nonrigid interfaces and nonzero Dw,/Dt-that is, with time-dependent con-

centration as viewed by an observer moving with the fluid. The systems considered

part (a) of

520.3

are thus included, because they are time-dependent for such an observer

(though steady for a stationary one).

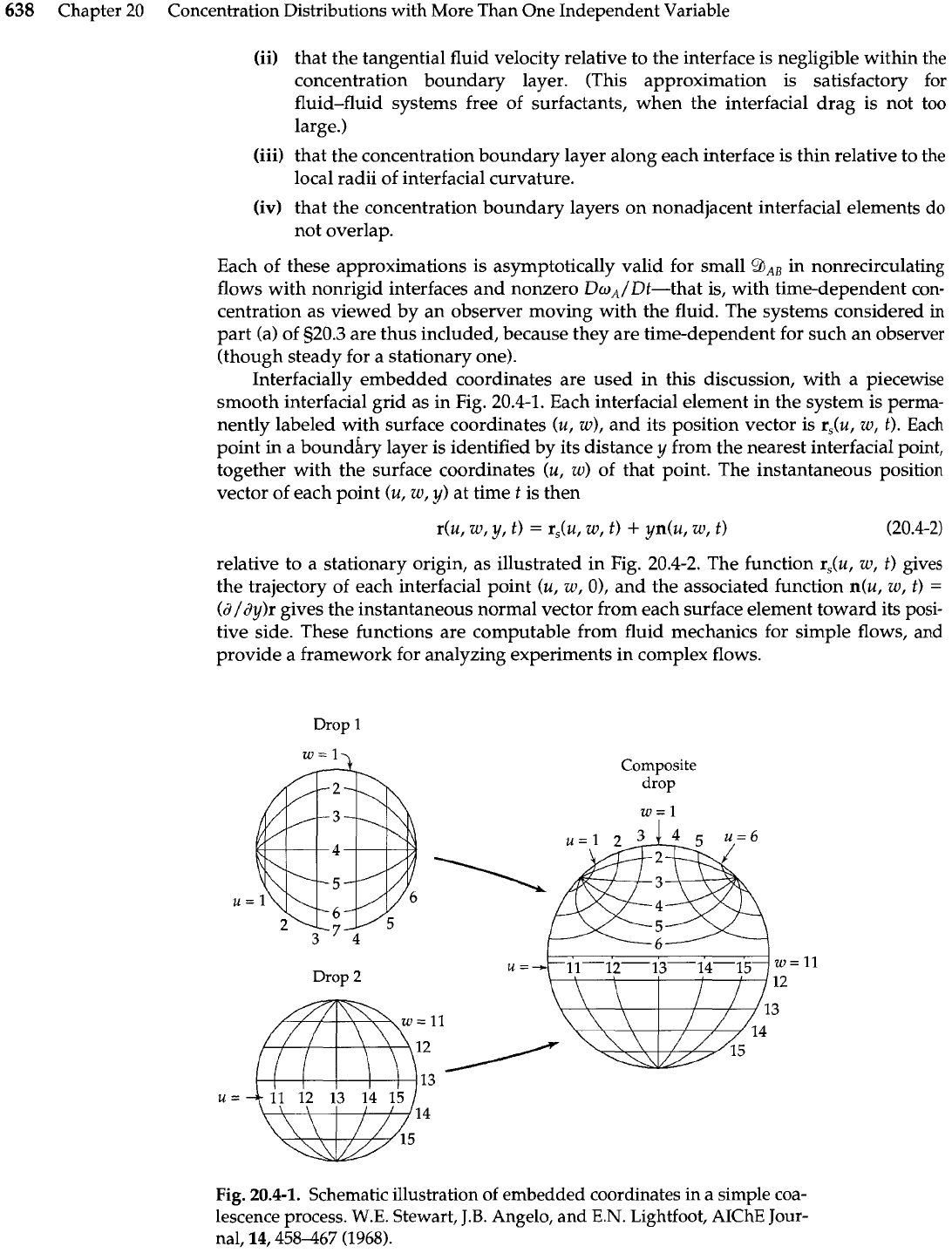
Interfacially embedded coordinates are used in this discussion, with a piecewise

smooth interfacial grid as in Fig. 20.4-1. Each interfacial element in the system is perma-

nently labeled with surface coordinates (u, w), and its position vector is r,(u, w, t). Each

point in a boundary layer is identified by its distance

from the nearest interfacial point,

together with the surface coordinates

(u,

of that point. The instantaneous position

vector of each point

(u,

at time t is then

relative to a stationary origin, as illustrated in Fig. 20.4-2. The function r,(u, w, t) gives

the trajectory of each interfacial point (u, w, O), and the associated function n(u, w,

(d/dy)r gives the instantaneous normal vector from each surface element toward its posi-

tive side. These functions are computable from fluid mechanics for simple flows, and

provide a framework for analyzing experiments in complex flows.

Drop

Composite

drop

Fig.

20.4-1.

Schematic illustration of embedded coordinates in a simple coa-

lescence process.

W.E.

Stewart,

J.B.

Angelo, and

E.N.

Lightfoot, AIChE Jour-

nal, 14,458467 (1968).

s20.4 Boundary Layer Mass Transport with Complex Interfacial Motion

639

Time

origin

Stationary

I+

coordinates

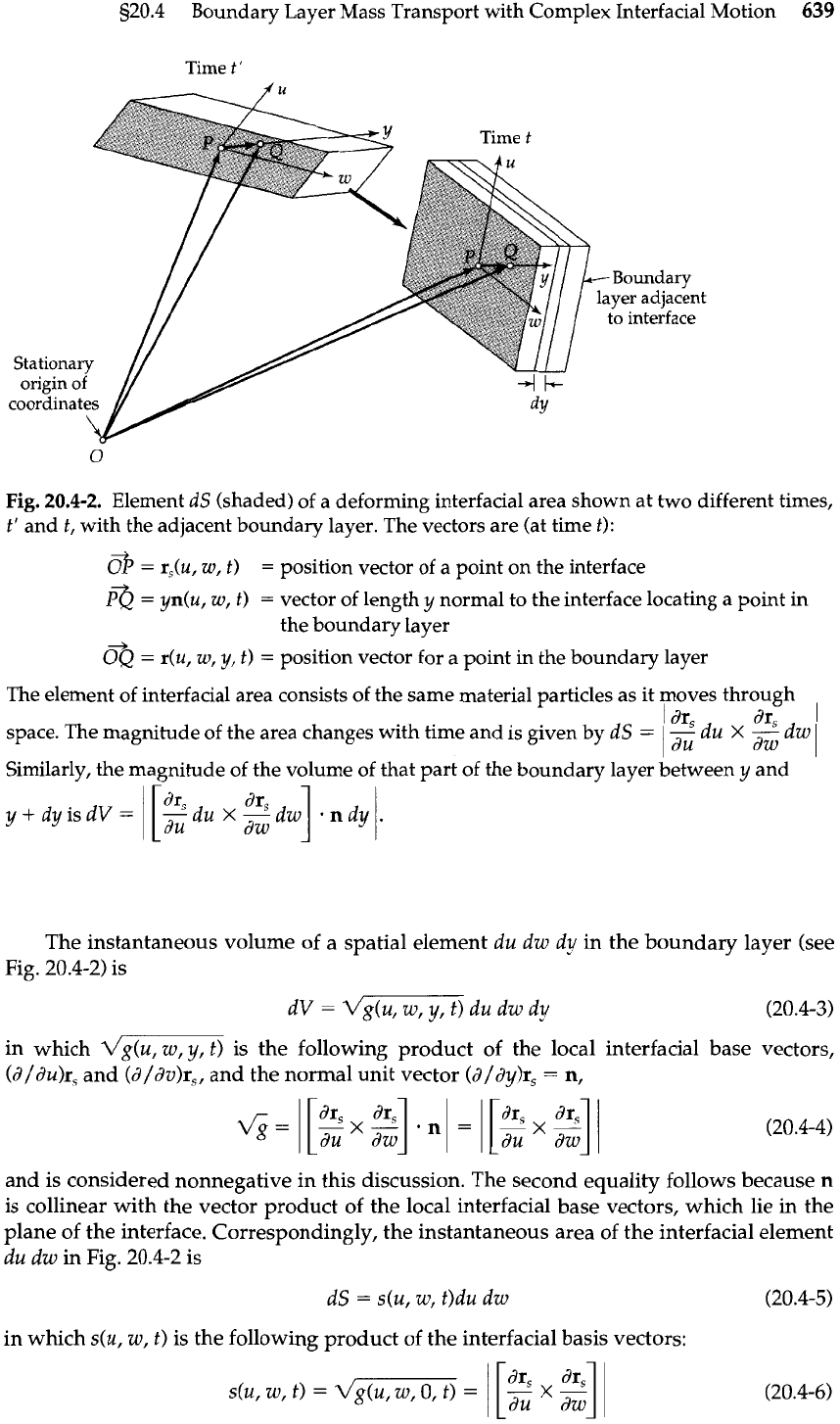
Fig.

20.4-2.

Element dS (shaded) of a deforming interfacial area shown at two different times,

t' and

with the adjacent boundary layer. The vectors are (at time t):

r&u, w,

position vector of a point on the interface

yn(u, w,

vector of lengthy normal to the interface locating a point in

the boundary layer

r(u,

position vector for a point in the boundary layer

The element of interfacial area consists of the same material particles as it moves through

space. The magnitude of the area changes with time and is given by dS

Similarly, the magnitude of the volume of that part of the boundary layer between y and

y+dyisdV=

The instantaneous volume of a spatial element

dw dy in the boundary layer (see

Fig.

20.4-2) is

vg(u,

y, t) du dw dy

(20.4-3)

in which dg(u, w,

t) is the following product of the local interfacial base vectors,

(d/du)r, and (d/dv)r,, and the normal unit vector (d/dy)r,

and is considered nonnegative in this discussion. The second equality follows because

is collinear with the vector product of the local interfacial base vectors, which lie in the

plane of the interface. Correspondingly, the instantaneous area of the interfacial element

du dw in Fig. 20.4-2 is

in which s(u, w,

is the following product of the interfacial basis vectors:

640

Chapter 20 Concentration Distributions with More Than One Independent Variable

In these interfacially embedded coordinates, the mass average velocity

relative to sta-

tionary coordinate axes takes the form

In this section, v is the mass average fluid velocity relative to an observer at (u,

y),

and

(d/at)r(u, w,

is the velocity of that observer relative to the stationary origin. Taking

the divergence of this equation gives the corollary2 (see Problem

20D.5)

This equation states that the divergence of

differs from that of v by the local rate of

ex-

pansion or contraction of the embedded coordinate frame.

The last term in

Eq.

20.4-8

arises when interfacial deformation occurs. Its omission in

such problems gives inaccurate predictions, which ~igbie~ and ~anckwerts~,~ then ad-

justed by introducing hypothetical surface residence times5f6 or surface rej~venation.~

Such hypotheses are not needed in the present analysis.

~pplication'of Eq.

20.4-8

and use of the constant-density condition

along with the no-slip condition on the tangential part of v, gives the derivative

Hence, the truncated Taylor expansion

describes the normal component of

in an incompressible fluid near a deforming

interface.

The corresponding expansion for the tangential part of v gives

in which

(u,

is the interfacial y-derivative of v

11.

With these results (neglecting

the

0(y2)

terms) and approximation (i), we can write

Eq.

20.4-1 for wA(u, w,

Here

(V,

is the surface divergence of

at the nearest interfacial point and is the sum

of the principal curvatures of the surface there. The

. .

stands for terms of higher

order, which are here neglected.

To select the dominant terms in Eq. 20.4-13, we introduce a dimensionless coordinate

Higbie,

Trans.

AIChE,

31,365-389 (1935).

Danckwerts,

ind.

Eng.

Chem.,

43,1460-1467 (1951).

Danckwerts,

AIChE

Journal,

1,456-463 (1955).

s20.4 Boundary Layer Mass Transport with Complex Interfacial Motion

641

in which

is an average thickness of the concentration boundary layer. When Eq. 20.4-14

is written in terms of this new variable, we get

for

in terms of u, w,

and

Since, on physical grounds,

will decrease with decreas-

ing

%ABf

the dominant terms for small

gAB

are those of lowest order in K-namely, all but

the

and

(V,

n) contributions. The subdominance of the latter terms confirms the as-

ymptotic validity of approximations (ii) and (iii) in non-recirculating flows.

Now, the coefficients of all the dominant terms must be proportional over the range

of BAB, in order that these terms remain of comparable size in the small-EbAB limit. Such a

"dominant balance principle" was applied previously in 513.6. Here it gives the orders

of magnitude

9AB/~2

o(1)

and

V~,/K

o(1)

(20.4-16, 17)

for the terms of the lowest order with respect to K. Equation 20.4-16 is consistent with the

previous examples of $power dependence of the diffusional boundary layer thickness

9,,

in free-surface flows. It also confirms the asymptotic correctness of assumption

(iv) for small values of aAB. Equation 20.4-17 is consistent with the proportionality of

to shown under Eq. 20.1-10 for the Arnold problem. Thus, the boundary layer

equation for

in either phase near a deforming interface is

to lowest order in

At the next order of approximation, terms proportional to

would

appear, and these involve the tangential velocity

and the interfacial curvature

(V,

n). The latter term appears in Problems 20C.1 and 20C.2.

Multiplication of Eq. 20.4-18 by p/MA (a constant for the assumptions made here),

and use of

as the coordinate normal to the interface as in Example 20.1-1, give the cor-

responding equation for the molar concentration cA(u, w, z,

which allows convenient extension of several earlier examples. Another useful corollary

is the binary boundary layer equation in terms of xA and

in which

and

9IAB

have been treated as constants, as in Example 20.1-1.

EXAMPLE

20.4-1

Mass Transfer with

Equation 20.4-19 readily gives a generalized form of

Eq.

20.1-65, by omitting the reaction

source term

and neglecting the normal velocity term

v,,

(thus assuming the interfacial

net mass flux to be small). The equation thus obtained has the form of Eq. 20.1-65, except

Nonuniform Interfacial

that the total surface growth rate

S/dt

is replaced by the local growth rate, given by

Deformation

In s(u, w, t)/dt. The resulting partial differential equation has two additional space vari-

ables

and w), but is solvable in the same manner, since no derivatives with respect to the

added variables appear.

642

Chapter 20 Concentration Distributions with More Than One Independent Variable

SOLUTION

Rewriting Eq. 20.1-66 with a boundary layer thickness function Nu, w, t) leads by analogous

steps to the relation

EXAMPLE

20.4-2

Gas Absorption with

Rapid Reaction and

Intetfacial Deformation

and the corresponding generalizations of Eqs. 20.1-71 and 72:

erf (20.4-22)

c~~

d4?bAB

[s(u,

~)/s(u,

t)12

These solutions, unlike Eq. 20.1-71 and Eq. 20.1-72, include the spatial variations of the

boundary layer thickness and interfacial molar flux NAZO that occur in nonuniform flows.

Local stretching of the interface (as at stagnation loci) thins the boundary layer and enhances

NAzO. Local interfacial shrinkage (at separation loci) diminishes NAz0, but also ejects stale fluid

from the boundary layer, allowing its mixing into the interior of the same phase. Observa-

tions of mass transler enhancement by such mixing have been interpreted by some workers

as "surface renewal," even though creation of new surface elements in an existing surface is

not permitted in continuum fluid mechanics.

These results, and others for negligible

v,,,

are obtainable conveniently by introducing

the following new variables into Eq. 20.4-19:

ZS(U,

W, t) and

(20.4-24/25)

In the absence of chemical reactions, the resulting differential equation for the concentration

function c,(u,

becomes

This is a generalization of Fick's second law to an asymptotic relation for forced convection in

free-surface flows.

Show how to generalize Example 20.1-2 to flow systems, by using Eq. 20.4-26 for the two re-

action-free zones.

SOLUTION

Using Eq. 20.4-26, we get the following replacements for Eqs. 20.1-26 and 27:

Now the reaction plane

z, of the original example is a time-dependent suuface,

Z,,

z,(u, w, t)

Z,/S(U,

t). The initial and boundary conditions remain as before, subject to this

generalization of the reaction-front location.

The solutions for

and cB then take the forms in Eqs. 20.1-35 and

36,

with z/lh replaced

z/G,

and

zR/~

qY.

The latter constant is again given by Eq. 20.1-37. The enhance-

ment of the absorption rate by the chemical reaction accordingly parallels the expressions that

will be given in Eq. 22.5-10, and simplified in Eqs. 22.5-11 through 13.

s20.5 "Taylor Dispersion" in Laminar Tube Flow

643

Fig.

20.5-1.

Sketch show-

Parabolic velocity

z=O profile in a circular tube

ing the axial spreading of

Pulse

injected

a concentration pulse in

here

Taylor dispersion in a

circular tube.

L/<vz>

520.5

"TAYLOR DISPERSION" IN LAMINAR

TUBE

FLOW

Here we discuss the transport and spreading of a solute "pulse" of material

intro-

duced into fluid

in steady laminar flow through a long, straight tube of radius

shown in Fig. 20.5-1.

pulse of mass

is introduced at the inlet

0 over a very short

period near time

0, and its progress through the tube is to be analyzed in the long-

time limit. Problems of this type arise frequently in process control (see Problem

20C.41,

medical diagnostic procedures,' and in a variety of environmental applications.2

short distance downstream from the inlet, the &dependence of the mass fraction

distribution will die out. Then the diffusion equation for oA(r,

t) in Poiseuille flow with

constant

and

a,,

takes the form

This equation is to be solved with the boundary conditions

B.C.

and 2:

~WA

atr=Oandatr=R,

(20.5-2)

which express the radial symmetry of the mass fraction profile and the impermeability of

the tube wall to diffusion. For this long-time analysis it is not necessary to speclfy the exact

shape of the pulse injected at

0. No exact analytical solution is available for the mass

fraction profile wA(r,

t)-even if an initial condition were clearly formulated-but Tay-

l0$r4 gave a useful approximate analysis that we summarize here. This involves getting

from Eq. 20.5-1 a partial differential equation for the cross-sectional average mass fraction

which can then be solved to describe the behavior at long times.

B. Bassingthwaighte and

A. Goresky, in Section

Volume 3 of

Handbook of Physiology,

2nd

edition, American Physiological Society, Bethesda, Md. (1984).

Chatwin and

Allen,

Ann.

Rev.

Fluid Mech.,

17,119-150 (1985); B.

Logan,

Environmental Transport Processes,

Wiley-Interscience, New York (1999), Chapters 10 and 11;

Seinfeld,

Advances in Chemical Engineering,

Academic Press, New York (1983),

pp.

209-299.

I. Taylor,

Proc. Roy. Soc.

A219,186-203 (1953).

G. I. Taylor,

Proc. Roy. Soc.,

A225,473-477 (1954).

644

Chapter

Concentration Distributions with More Than One Independent Variable

Taylor began by neglecting the axial molecular diffusion term (dashed underlined

term in Eq. 20.5-I), and subsequently showed4 that this is permissible if the P6clet num-

ber PhAB

R(vZ)/9IAB is of the order of 70 or greater, and if the length

Lp(t)

of the region

occupied by the pulse, measured visually in Taylor's experimentsf3 is of the order of

170R or greater. Here (v,)

$v,,,,~

is the mean speed of the flow.

Taylor sought a solution valid for long times. He estimated the condition for the va-

lidity of his result to be

When the pulse length

attains this range, enough time has elapsed that the initial

shape of the pulse no longer matters.

In order to follow the development of the concentration profile as the fluid moves

downstream, it is useful to introduce the shifted axial coordinate

When this is used in Eq. 20.5-1 (without the dashed-underlined term), we get the follow-

ing diffusion equalion for wA(rf

t),

in which

r/R is the dimensionless radial coordinate. The time derivative here is under-

stood to be taken at constant

and, under the condition of Eq. 20.5-4, it may be neglected

relative to the radial diffusion term. As a result we have a quasi-steady-state equation

For the condition of Eq. 20.5-4, the mass fraction can be expressed as

where (w,) is a function of

and

Substituting this expression into the right side of

Eq.

20.5-7, and accordingly neglecting wi, we then get

from which the radial dependence of the mass fraction can be obtained under the condi-

tion of Eq. 20.5-4.

Integration of Eq. 20.5-9 with the boundary conditions of Eq. 20.5-2 then yields

The average of this profile over the cross section is

Subtracting this equation from the previous one, and replacing

v,,,,,

by 2(vz), gives finally

as Taylor's approximate solution of Eq. 20.5-6.

520.5

"Taylor Dispersion" in Laminar Tube Flow

645

The total mass flow of

through a plane of constant

(that is, the flow relative to

the average velocity

(v,))

Next we note that, with the assumption of

constant,

p(wA(vz))

(pA)(v,)

and

p(oAvz)

(pAvA,)

(nAz).

(Replacing

VAz

is allowed here because, with axial mol-

ecular diffusion neglected, species

and

are moving with the same axial speed).

Therefore when Eq. 20.5-13 is divided by

TR~,

we obtain the averaged mass flux

expression

relative to stationary coordinates. Here

is an

axial

dispersion coefficient, given by Tay-

lor's analysis as

This formula indicates that axial dispersion (in the range

considered so far) is

enhanced by the radial variation of

and reduced by radial molecular diffusion.

Although Eq. 20.5-14 has the form of Fick's law in Eq.

(C)

of Table

17.8-2,

the present

equation does not include any axial molecular diffusion. Also it should be emphasized

that

is not a property of the fluid mixture, but depends on

and

(v,)

as well as on

%,,.

Next we write the equation of continuity of Eq. 19.1-6, averaged over the tube cross

section, as

When the expression for the mass flux of

from Eq. 20.5-14 is inserted, we get the fol-

lowing

axial

dispersion equation:

This equation can be solved to get the shape of the traveling pulse resulting from a

function input of a mass

of solute

into a stream of otherwise pure

This can be used along with Eq. 20.5-15 to extract

gAB

from data on the concentrations in

the traveling pulse. In fact, this is probably the best method for reasonably quick mea-

surements of liquid diffusivities.

Taylor's development laid the foundation for an extensive literature on convective dis-

persion. However, it remained to study the approximations made and to determine their

range of validity. ~ris~ gave a detailed treatment of dispersion in tubes and ducts, covering

the full range of t and including diffusion

the

and

directions. His long-time asymptote

Aris,

PYOC.

Roy.

SOC.,

A235,67-77

(1956).

646

Chapter 20 Concentration Distributions with More Than One Independent Variable

.01 0.1 1.0 10 100

Dimensionless time

QA~t/~'

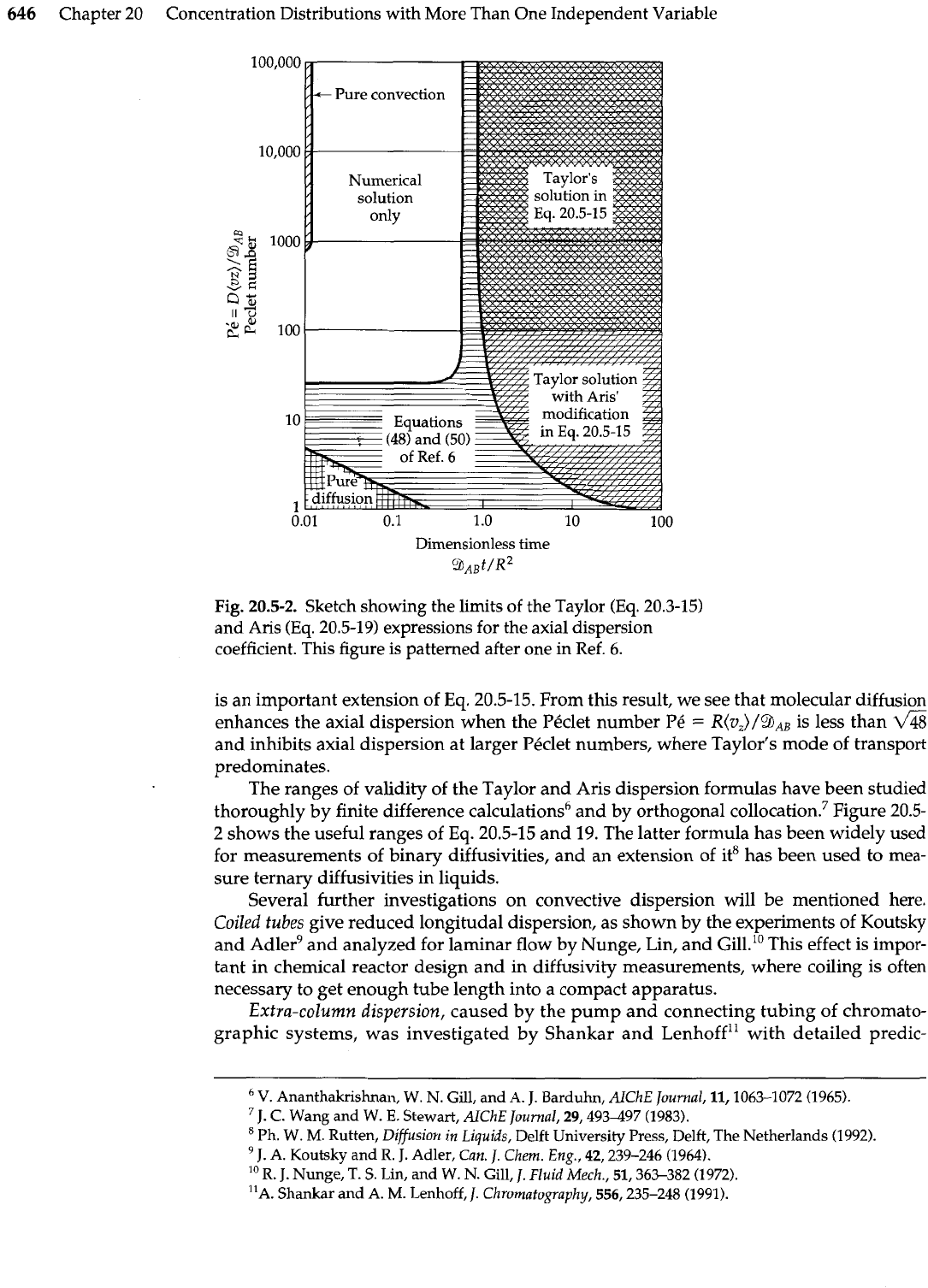
Fig.

20.5-2.

Sketch showing the limits of the Taylor

(Eq.

20.3-15)

and Aris

(Eq.

20.5-19) expressions for the axial dispersion

coefficient. This figure is patterned after one in Ref.

is an important extension of

Eq.

20.5-15. From this result, we see that molecular diffusion

enhances the axial dispersion when the Pkclet number Pk

R(V,)/%~

is less than

V'%

and inhibits axial dispersion at larger Peclet numbers, where Taylor's mode of transport

predominates.

The ranges of validity of the Taylor and Aris dispersion formulas have been studied

thoroughly by finite difference calculationsb and by orthogonal coll~cation.~ Figure

20.5-

2 shows the useful ranges of

Eq.

20.5-15 and

19.

The latter formula has been widely used

for measurements of binary diffusivities, and

extension

it8 has been used to mea-

sure ternary diffusivities in liquids.

Several further investigations on convective dispersion will be mentioned here.

Coiled tubes

give reduced longitudal dispersion, as shown by the experiments of Koutsky

and Adler9 and analyzed for laminar flow by Nunge, Lin, and Gill.'' This effect is impor-

tant in chemical reactor design and in diffusivity measurements, where coiling is often

necessary to get enough tube length into a compact apparatus.

Extra-column

dispersion,

caused by the pump and connecting tubing of chromato-

graphic systems, was investigated by Shankar and ~enhoff" with detailed predic-

Ananthakrishnan, W.

Gill,

and A.

Barduhn,

AlChE Journal,

11,1063-1072 (1965).

Wang and

Stewart,

AKhE Journal,

29,493497 (1983).

Ph. W.

Rutten,

Diffusion

in Liquids,

Delft University Press, Delft, The Netherlands

(1992).

A. Koutsky and

Adler,

Can. J. Chem.

Eng.,

42,239-246 (1964).

Nunge,

Lin, and W.

Gill,

Fluid Mech.,

51,363-382 (1972).

"A. Shankar and A.

Lenhoff,

Chromatography,

556,235-248 (1991).