Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena
Подождите немного. Документ загружается.


Questions for Discussion
647
tions and precise experiments. Their experiments showed that the form of radial av-
eraging is important at times shorter than the recommended range shown in Fig.
20.5-2 for the Taylor-Aris formula. Depending on the type of analyzer used, the data
may be better described either by a cup-mixing average
p,b
or by the area average
(p,)
used above.
Hoagland and Prud'homme12 have analyzed laminar longitudinal dispersion in
tubes of sinusoidally varying radius, R(z)
=
R,(1
f
E
sin(2m/A)), to model dispersion in
packed-bed processes. Their results parallel Eq. 20.5-19, when the variations have small
relative amplitude
8
and long relative wavelength
A/&.
One might think that the axial
dispersion in a packed column would be similar to that in tubes of sinusoidally varying
radius, but that is not the case. Instead of Eq. 20.3-19, one finds
K
.=
2.59,,PeAB, with the
first power of the P6clet number appearing, instead of the second power and with
K
in-
dependent of
9JAB.13
Brenner and Edwards14 have given analyses of convective disper-
sion and reaction in various geometries, including tubes and spatially periodic packed
beds.
Dispersion has also been investigated in more complex flows. For turbulent flows in
straight tubes, Taylor15 derived and experimentally verified the axial dispersion formula
K/Rv*
=
10.1, where
v*
is the friction velocity used in Eq. 5.3-2. Bassingthwaighte and
Goresky' investigated models of solute and water exchange in the cardiovascular sys-
tem, and Chatwin and Allen2 give mathematical models of turbulent dispersion in rivers
and estuaries.
Equations 20.5-1 and 19 are limited to the conditions of Eqs. 20.5-2 and
4.
Therefore,
they are not appropriate for describing entrance regions of steady-state reactor opera-
tions or systems with heterogeneous reactions. Equation 20.5-1 is a better starting point
for laminar flows.
QUESTIONS FOR DISCUSSION
1.
What experimental difficulties might be encountered in using the system in Example 20.1-1 to
measure gas-phase diffusivities?
2.
What problems do you foresee in using the Taylor dispersion technique of s20.5 for measur-
ing liquid-phase diffusivities?
3.
Show that Eq. 20.1-16 satisfies the partial differential equation as well as the initial and
boundary conditions.
4.
What do you conclude from Table 20.1-l?
5.
Why are Laplace transforms useful in solving the problem in Example 20.1-3? Could Laplace
transforms be used to solve the problem in Example 20.1-I?
6.
How is the velocity distribution in Example 20.1-4 obtained?
7.
Describe the method of solving the variable surface area problem in Example 20.1-4.
8.
Perform the check suggested after
Eq.
20.1-74.
9.
What effects do chemical reactions have on the boundary layer?
10.
Discuss the Chilton-Colburn expressions in Eq. 20.2-57. Would you expect these same rela-
tions to be valid for flows around cylinders and spheres?
''
D. A.
Hoagland and
R.
K.
Prud'homme,
AlChE
Journal,
31,236-244
(1985).
l3
A.
M.
Athalye,
J.
Gibbs, and
E.
N.
Lightfoot,
J.
Chromatog.
589,71-85
(1992).
l4
H.
Brenner and
D.
A. Edwards,
Macrotransport Processes,
Butterworth-Heinemann, Boston (1993).
l5
G.
I.
Taylor,
Proc.
Roy.
Soc.,
A223,446467
(1954).

648
Chapter 20
Concentration Distributions with More Than One Independent Variable
PROBLEMS
20A.1.
Measurement of diffusivity by unsteady-state evaporation. Use the following data to
determine the diffusivity of ethyl propionate (species
A)
into a mixture of 20 mole% air and
80 mole% hydrogen (this mixture being treated as a pure gas
B).'
Increase in vapor volume (cm3)
~
(sl")
These data were obtained1 by using a glass tube 200 cm long, with an inside diameter 1.043
cm; the temperature was 27.9OC and the pressure 761.2 mm Hg. The vapor pressure of ethyl
propionate at this temperature is 41.5 mm Hg. Note that
t
is the actual time from the start of
the evaporation, whereas the volume increase is measured from
t
=.
240 s.
20A.2.
Absorption of oxygen from a growing bubble (Fig. 20A.2). Oxygen is being injected into
pure water from a capillary tube. The system is virtually isothermal and isobaric at 25OC and
1
atm. The solubility of oxygen in the liquid phase is
o,,
=
7.78
X
and the liquid-phase
diffusivity for the oxygen-water pair is
9,,
=
2.60
X
cm2/s. Calculate the instantaneous
total absorption rate in g/s, for a bubble of 1 mm diameter and age
t
=
2 s, assuming
(a) Constant volumetric growth rate
(b) Constant radial growth rate
drJdt
Fig.
20A.2.
Gas absorption from a
growing bubble, idealized as a sphere.
Answers:
(a)
7.6
X
lo-'
g/s; (b) 1.11
X
lop7
g/s
20A.3.
Rate of evaporation of n-octane. At 20°C, how many grams of liquid n-octane will evaporate
into
N2
in 24.5
hr
in a system such as that studied in Example 20.1-1 at system pressures of
(a)
1 atm, and (b) 2 atm? The area of the liquid surface is 1.29 cm2, and the vapor pressure of
n-
octane at 20°C is 10.45 mm Hg.
Answer:
(a) 6.71 mg
D.
F. Fairbanks
and
C.
R.
Wilke,
Ind.
Eng.
Chem.
42,471475
(1950).

Problems
649
20A.4. Effect of bubble size on interfacial composition (Fig. 20A.2). Here we examine the assump-
tion of time-independent interfacial composition, WA~, for the system in Fig. 20A.2. We note
that, because of the interfacial tension, the gas pressure
p,
depends on the instantaneous
bubble radius
r,.
The equilibrium expression
is adequate unless dr,/dt is very large. Here
p,
is the ambient liquid pressure at the mean ele-
vation of the bubble, and
CT
is the interfacial tension.
For a sparingly soluble solute, the interfacial liquid composition
WAO
depends on pA ac-
cording to Henry's law
in which the Henry's law constant,
H,
depends on the two species and on the liquid tempera-
ture and pressure. This expression may be combined with
Eq.
20A.4-1 to obtain the depen-
dence of
w,,
on r,.
For a gas bubble dissolving in liquid water to
T
=
25OC and p,
=
1
atm, how small must
the bubble be in order to obtain a 10% increase in above the value for a very large bubble?
Assume
u
=
72 dyn/cm over the relevant composition range.
Answer: 1.4 microns
20A.5. Absorption with rapid second-order reaction (Fig. 20.1-2). Make the following calculations
for the reacting system depicted in the figure:
(a)
Verify the location of the reaction zone, using Eq. 20.1-37.
(b) Calculate NAO at
t
=
2.5 s.
20A.6. Rapid forced-convection mass transfer into a laminar boundary layer. Calculate the evapo-
ration rate nAo(x) for the system described under Eq. 20.2-52, given that
w,,
=
0.9,
w,,
=
0.1,
n&)
=
0 and Sc
=
2.0. Use Fig. 22.8-5 with
R
calculated as
R,
from
Eq.
20.2-51, to find the di-
mensionless mass flux (denoted by
4,
for diffusional calculations with mass fractions).
Then use
Eq.
22.8-21 and Table 20.2-1 to calculate
K,
and
Eq.
20.2-48 to calculate nAo(x).
Answer: nAo(x)
=
0.33a
20A.7. Slow forced-convection mass transfer into a laminar boundary layer. This problem illus-
trates the use of Eqs. 20.2-55 and 57 and tests their accuracy against that of
Eq.
20.2-47.
(a) Estimate
the
local evaporation rate, n,, as a function of
x
for the drying of a porous water-
saturated slab, shaped as in Fig. 20.2-2. The slab is being dried in a rapid current of air, under
conditions such that
w,,
=
0.05,
w,,
=
0.01, and
Sc
=
0.6. Use Eq. 20.2-55 for the calculation.
(b) Make an alternate calculation of
n,,
using
Eq.
20.2-57.
(c)
For comparison with the preceding approximate results, calculate
n,,
from Eq. 20.2-47
and Table 20.2-1. The
K
values found in (a)
will
be sufficiently accurate for looking up
II'(0,
Sc,
K).
Answers: (a) nA0(x)
=
0.0188w; (b) nAO(x)
=
0.0196-;
(c)
nA0(x)
=
0.0188-
20B.1. Extension of the Arnold problem to account for interphase transfer of both species. Show
how
to
obtain Eqs. 20.1-23,24, and 25 starting with the equations of continuity for species
A
and
B
(in molar units) and the appropriate initial and boundary conditions.
20B.2. Extension of the Arnold problem to nonisothermal diffusion. In the situation described in
Problem 20B.1, find the analogous result for the temperature distribution T(z,
f).
(a) Show that the energy equation [Eq.
(H)
of Table 19.2-41 reduces to
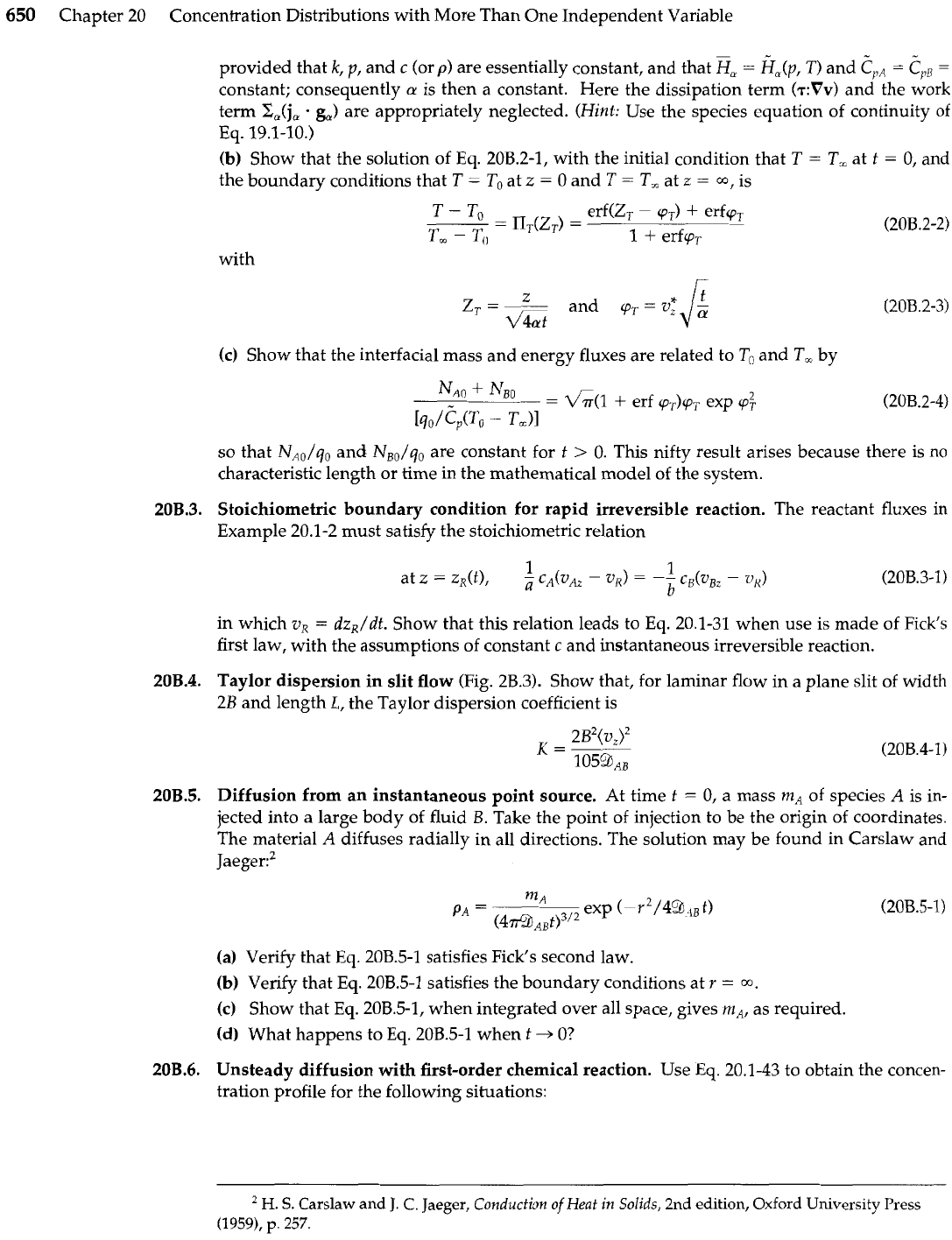
650
Chapter 20
Concentration Distributions with More Than One Independent Variable
provided that
k,
p,
and
c
(or
p)
are essentially constant, and that
=
&(p,
T)
and
C,,
=
G,
=
constant; consequently
a
is then a constant. Here the dissipation term
(7:Vv)
and the work
term
CJj,
.
gJ
are appropriately neglected.
(Hint:
Use the species equation of continuity
of
Eq. 19.1-10.)
(b) Show that the solution of Eq. 208.2-1, with the initial condition that
T
=
T,
at
t
=
0, and
the boundary conditions that
T
=
To
at
z
=
0 and
T
=
T,
at
z
=
a,
is
with
r
z
Z,
=
--
and
qr
=
v:
V'G
(c)
Show that the interfacial mass and energy fluxes are related to
To
and
T,
by
so that
NAo/qo
and
NRo/qo
are constant for
t
>
0.
This nifty result arises because there is
no
characteristic length or time in the mathematical model of the system.
Stoichiometric boundary condition for rapid irreversible reaction. The reactant fluxes in
Example 20.1-2 must satisfy the stoichiometric relation
in which
vR
=
dzR/dt.
Show that this relation leads to Eq. 20.1-31 when use is made of Fick's
first law, with the assumptions of constant
c
and instantaneous irreversible reaction.
Taylor dispersion in slit flow (Fig. 2B.3). Show that, for laminar flow in a plane slit of width
2B and length
L,
the Taylor dispersion coefficient is
Diffusion from an instantaneous point source. At time
t
=
0, a mass
m,
of species
A
is in-
jected into a large body of fluid
B.
Take the point of injection to be the origin of coordinates.
The material
A
diffuses radially in all directions. The solution may be found in Carslaw
and
~aeger:~
(a)
Verify that Eq. 20B.5-1 satisfies Fick's second law.
(b) Verify that Eq. 20B.5-1 satisfies the boundary conditions at
r
=
w.
(c)
Show that Eq. 20B.5-1, when integrated over all space, gives
m,,
as required.
(d) What happens to Eq. 20B.5-1 when
t
+
O?
Unsteady diffusion with first-order chemical reaction. Use Eq. 20.1-43 to obtain the concen-
tration profile for the following situations:
H.
S.
Carslaw and
J.
C. Jaeger,
Conduction of
Heat
in Solids,
2nd edition, Oxford University Press
(1959),
p.
257.

Problems
651
(a) The catalyst particle of Problem 188.14, in time-dependent operation with the boundary
conditions as given before, but with the initial condition that
c,
=
0
at
t
=
0.
The differential
equation for
CA
is
where
is the interior void fraction for the particle. The necessary solution with
kra
=
0 may
be found from the result of Example 12.1-2.
(b) Diffusion and reaction of a solute,
A,
injected at
t
=
0 at the point
r
=
0 (in spherical coor-
dinates) in an infinite stationary medium. Here the functiong of Eq. 20.1-43 is given as
and the function
f
vanishes.
20B.7.
Simultaneous momentum, heat, and mass transfer: alternate boundary conditions (Fig.
20B.7). The dimensionless profiles
Nq,
A,
K)
in Eq. 20.2-43 are applicable to a variety of situ-
ations. Use Eqs. 20.2-49 to
52
to obtain implicit equations for the evaluation of the dimension-
less net mass flux
K
for the following steady-state operations:
(a) Evaporation of pure liquid
A
from a saturated porous plate into a gaseous stream of
A
and
B.
Substance
B
is insoluble in liquid
A.
(b) Instantaneous irreversible reaction of gas
A
with a solid plate of
C
to give gaseous
B,
ac-
cording to the reaction
A
+
C
+
2B.
The molecular weights of
A
and
B
are equal.
(c)
Transpiration cooling of a porous-walled hollow plate, as shown in the figure. The fluid is
pure
A
throughout, and the injected fluid is distributed so as to maintain the whole outer sur-
face of the plate at a uniform temperature
To.
Approaching stream of
gas
A
at temperature
T,
and velocity
v,
b
Injection velocity
vo
(x)
Surface at uniform
A
temperature
To
It*
/
Porous wall
\
-
'
,-Gas
A
at uniform temperature
T,
-
Gas
A
in
I+y
Porous wall
/
Fig.
20B.7.
A
transpiration-cooled
porous plate.
Answers:
(a)
K
=
-
(W~O
-
@,")nr
(0,
SC,
N;
(b)
)K
=
1
II
(0,
SC,
K)
Sc
1
-
o,,
Sc

652
Chapter 20
Concentration Distributions with More Than One Independent Variable
20B.8.
Absorption from a pulsating bubble. Use the results of Example 20.1-4 to calculate 6(t) and
NAO(t) for a bubble whose radius undergoes a square-wave pulsation:
r,
=
R,
for 2n
<
wt
<
2n
+
1
r,
=
R,
for 2n
+
1
<
ot
<
2n
+
2
Here
w
is a characteristic frequency, and
n
=
0,1,2,
. . . .
20B.9.
Verification of
the
solution of the Taylor-dispersion equation. Show that the solution to Eq.
20.5-17, given in Eq. 20.5-18, satisfies the differential equation, the initial condition, and the
boundary
condition^.^
The latter are that at
z
=
?
m,
d
(PA)
=
0 and
,~z
bA)
=
0
The initial condition is that, at t
=
0, the solute pulse, of mass mA, is concentrated at
z
=
0,
with no solute anywhere else in the tube, so that for all times,
(a) Show that Eq. 20.5-17 can be reduced to the one-dimensional form of Fick's second law by
the coordinate transformation
(b) Show that Eq. 20.5-18 satisfies the equation derived in (a).
(c)
Show that Eqs. 20B.9-1 and 2 are also satisfied.
20C.1.
Order-of-magnitude analysis of gas absorption from a growing bubble (Fig. 20A.2).
(a) For the growth of the spherical bubble of Problem 20A.2(a) in a liquid of constant density,
show that in the liquid phase the radial velocity is
v,
=
C,/r2
according to the equation of con-
tinuity. Then use the boundary condition that
v,
=
drJdt
at r
=
rs(t) to obtain
(b) Next, using the species equation of continuity in spherical coordinates with diffusion in
the radial direction only, show that
and indicate suitable initial and boundary conditions.
(c)
For short contact times, the effective diffusion zone is a relatively thin layer, so that it is
convenient to introduce a variable
y
=
r
-
r,(t).
Show that this leads to
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(d) From Example 20.1-4 we can see that the contributions of terms
(11,
(2), and
(4)
are all
of
the same order of magnitude in the concentration boundary layer, that is, at
y
=
O(6,)
=
o(-). Taking these terms to be of order 0(1), estimate the orders of magnitude of the
re-
maining terms shown in Eq. 20C.1-3.
See, for example,
H.
S.
Carslaw and
J.
C. Jaeger,
Heat Conduction in Solids,
2nd edition,
Oxford
University Press (1959),§10.3. For the effects of finite
tube
length, see
H.
Brenner,
Ckem. Eng. Sci.,
17,
229-243 (1961).

Problems
653
(el
Show that the terms of the two leading orders in Eq. 20C.l-3 give
-..--
----------
the second-order terms being designated by dashed underlines.
(e)
This equation has been analyzed thoroughly in the electrochemical literat~re.~ The results
for nAo are further considered in Problem 20C.2.
20C.2. Effect of surface curvature on absorption from a growing bubble
(Fig. 20A.2). Pure gas
A
is
flowing from a small capillary into a large reservoir of initially pure liquid
B
at a constant
molar flow rate WA. The interfacial molar flux of
A
into the liquid is predictable from the
Levich-Koutecky-Newman equation
in which
for purely radial motion and a spherical bubble. Equation 20C.2-1 is a consequence of Eq.
20C.1-4.
(a)
Give an expression for the number of moles of
A
absorbed over a bubble lifetime to.
(b)
Use
Eq.
20C.2-1 to obtain more accurate results for the absorption rates in Problem 20A.2.
20C.3. Absorption with chemical reaction in a semi-infinite medium.
A
semi-infinite medium of
material
B
extends from the plane boundary
x
=
0 to
x
=
m.
At time t
=
0 substance
A
is
brought into contact with this medium at the plane
x
=
0, the surface concentration being cA,
(for absorption of gas
A
by liquid
B,
for example, c~, would be the saturation concentration).
Substances
A
and
B
react to produce
C
according to the irreversible first-order reaction
A
+
B
+
C.
It is assumed that
A
is present in such a small concentration that the equation describing
the diffusion plus chemical reaction process is
in which
k;'
is the first-order rate constant. This equation has been solved for the initial condi-
tion that
CA
=
0 at
t
=
0, and the boundary conditions that
cA
=
c,,
at
x
=
0, and cA
=
0
at
x
=
w
.
The solution is5
(a)
Verify that Eq. 20C.3-2 satisfies the differential equation and the boundary conditions.
(b)
Show that the molar flux at the interface
x
=
0 is
J.
Kouteckj,
Czech.
1.
Phys.,
2,50-55 (1953). See also
V.
Levich,
Physicochemical Hydrodynamics,
2nd
edition, Prentice-Hall, Englewood Cliffs,
N.J.
(1962). The right sides of Levich's Eqs. 108.17 and 108.18
should be multiplied
by
t2'!
See also
J.
S.
Newman,
ElectrochemicaI Systems,
2nd edition, Prentice-Hall,
Englewood Cliffs,
N.J.
(1991).
P.
V.
Danckwerts,
Trans. Faraday
Soc.,
46,300-304 (1950).

654
Chapter 20
Concentration Distributions with More Than One Independent Variable
(c)
Show further that the total moles absorbed across area
A
up to time
t
is
(d) Show that, for large values of kyt, the expression in (c) reduces asymptotically to
This result6 is good within
2%
for values of kyt greater than 4.
20C.4.
Design of fluid control circuits. It is desired to control a reactor via continuous analysis of
a
side stream. Calculate the maximum frequency of concentration changes that can be detected
as
a
function of the volumetric withdrawal rate, if the stream is drawn through a 10 cm length
of tubing with an internal diameter of 0.5 mm. Suggestion: Use as a criterion that the standard
deviation of a pulse duration be no more than
5%
of the cycle time to
=
2n-/w, where
w
is the
frequency it is desired to detect.
20C.5.
Dissociation of a gas caused
by
a temperature gradient. A dissociating gas (for example,
Na,
+
2Na) is endosed in a tube, sealed at both ends, and the two ends are maintained at dif-
ferent temperatures. Because of the temperature gradient established, there will be a continu-
ous flow of Na, molecules from the cold end to the hot end, where they dissociate into
Na
atoms, which in turn flow from the hot end to the cold end. Set up the equations to find the
concentration profiles. Check your results against those of Dira~.~
20D.1.
Two-bulb experiment for measuring gas
diffusivities-analytical
solution (Fig. 188.6).
This experiment, described in Problem 18B.6, is analyzed there by a quasi-steady-state
method. The method of separation of variables gives the exact solution8 for the compositions
in the two bulbs as
in which
y,,
is the nth root of
y
tan
y
=
N, and N
=
SL/V. Here the
2
sign corresponds to the
reservoirs attached at
t
L.
Make a numerical comparison between Eq. 20D.1-1 and the experi-
mental measurements of
and re^.^
Also compare Eq. 20D.1-1 with the simpler result in
Eq.
18B.6-4.
20D.2.
Unsteady-state interphase diffusion. Two immiscible solvents I and I1 are in contact at the
plane
z
=
0. At time
t
=
0 the concentration of
A
is
c,
=
cf
in phase
I
and c,,
=
cg
in phase
11.
For t
>
0 diffusion takes place across the liquid-liquid interface. It is to be assumed that the
solute is present only in small concentration in both phases, so that Fick's second law of diffu-
sion is applicable. We therefore have to solve the equations
R.
A.
T.
0.
Nijsing,
Absovptie van gassen in vloeistoffen, zonder en met chemische reactie,
Academisch
Proefschrift, Technische Universiteit Delft (1957).
P.
A.
M.
Dirac,
Proc. Camb. Phil. Soc.,
22,
Part 11,132-137 (1924). This was Dirac's first publication,
written while he was a graduate student.
R.
B.
Bird,
Advances in Chemical Engineering,
Vol. 1, Academic Press, New York (1956),
pp.
156-239;
errata, Vol.
2
(1958),
p.
325.
The result at the bottom of
p.
207 is in error, since the factor of
(-1)""
is
missing. See also
H.
S.
Carslaw and
J.
C. Jaeger,
Conduction of Heat in Solids,
2nd
edition, Oxford
University Press (1959),
p.
129.
S.
P.
S.
Andrew,
Chem. Eng. Sci.,
4,269-272 (1955).

Problems
655
in
which
c1
and
cII
are the concentrations of
A
in phases
I
and
11,
and
and
BII
are the corre-
sponding diffusivities. The initial and boundary conditions are:
atz
=
-w,
cI
=
cp
atz
=
+w,
CII
=
cPI
The first boundary condition at
z
=
0
is the statement of equilibrium at the interface,
m
being
the "distribution coefficient" or "Henry's law constant." The second boundary condition is a
statement that the molar flux calculated at
z
=
0-
is the same as that at
z
=
0';
that
is,
there is
no loss of
A
at the liquid-liquid interface.
(a) Solve the equations simultaneously by Laplace transform or other appropriate means to
obtain:
(b)
Obtain the expression for the mass transfer rate at the interface.
20D.3.
Critical
size
of an autocatalytic
system.
It is desired to use the result of Example 20.1-3 to dis-
cuss the critical size of a system in which an "autocatalytic reaction" is occurring. In such a sys-
tem the reaction products increase the rate of reaction. If the ratio of the system surface to the
system volume
is
large, then the reaction products tend to escape from the boundaries of the sys-
tem. If the surface to volume ratio is small, however, the rate of escape may be less
than
the rate
of creation, and the reaction rate
will
increase rapidly. For a system of a given shape, there
will
be a critical size for which the rate of production just equals the rate of removal.
One example is that of nuclear fission. In a nuclear pile the rate of fission depends on the
local neutron concentration. If neutrons are produced at a rate that exceeds the rate of escape
by diffusion, the reaction is self-sustaining and a nuclear explosion occurs.
Similar behavior is also encountered in many chemical systems, although the behavior
here is generally more complicated. An example is the thermal decomposition of acetylene
gas, which is thermodynamically unstable according to the overall reaction.
This reaction appears to proceed by a branched-chain, free-radical mechanism, in which the
free radicals behave qualitatively as the neutrons in the preceding paragraph, so that the de-
composition is autocatalytic.
However, the free radicals are effectively neutralized by contact with an iron surface, so
that the free-radical concentration is maintained near zero at such a surface. Acetylene gas
can then be stored safely in an iron pipe below a "critical" diameter, which is smaller the
higher the pressure or temperature of the gas. If the pipe is too large, the formation of even
one free radical is likely to cause a rapidly increasing rate of decomposition, which may result
in a serious explosion.
(a)
Consider a system enclosed in a long cylinder in which the diffusion and reaction process
is described by
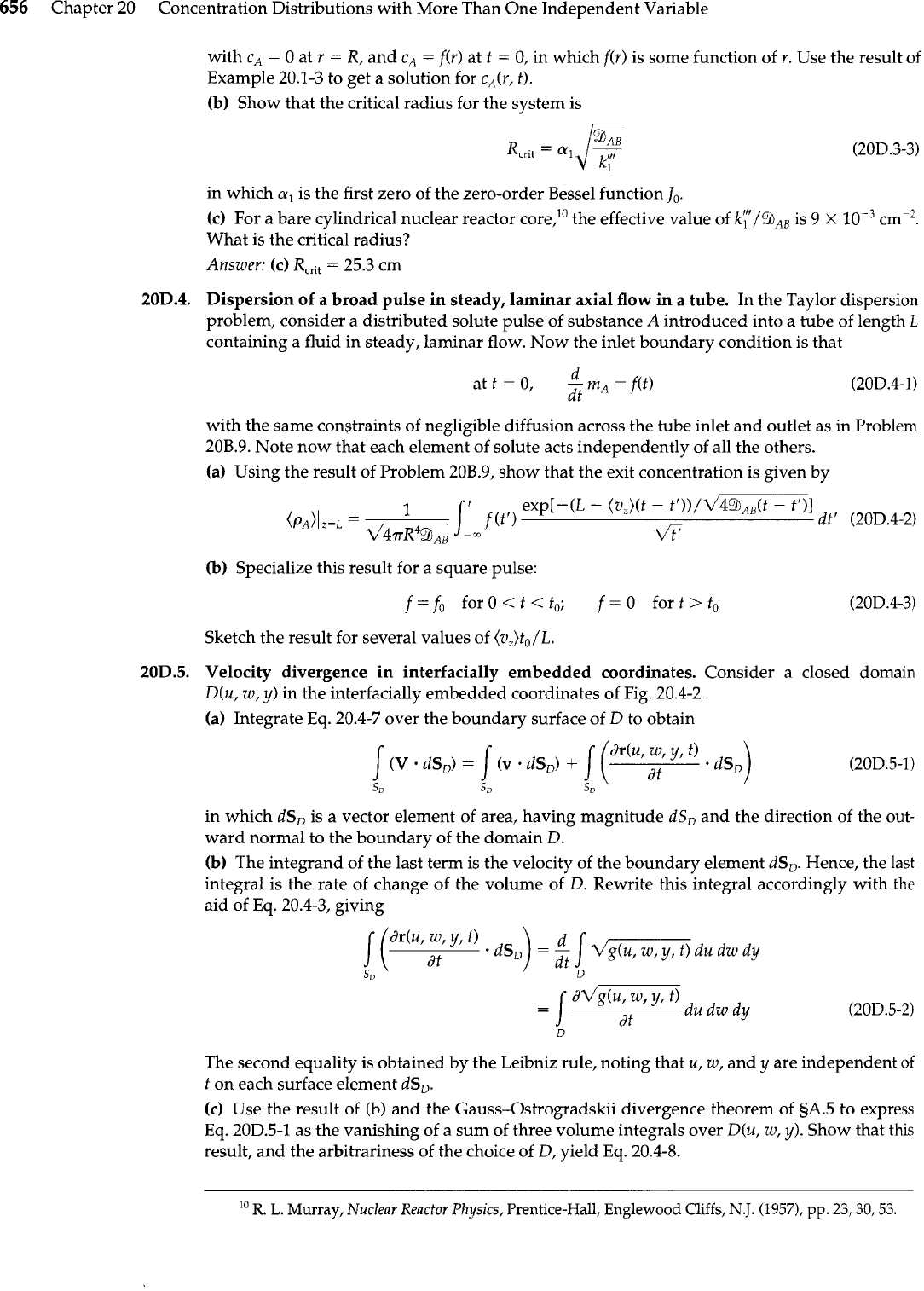
656
Chapter 20 Concentration Distributions with More Than One Independent Variable
with cA
=
0 at r
=
R, and
CA
=
f(r) at
t
=
0, in which f(r) is some function of r. Use the result of
Example 20.1-3 to get a solution for cA(r,
t).
(b) Show that the critical radius for the system is
in which
a,
is the first zero of the zero-order Bessel function
1,.
(c)
For a bare cylindrical nuclear reactor core,'' the effective value of
k:))/gAB
is 9
X
~m-~.
What is the critical radius?
Answer: (c) R,,
=
25.3 cm
20D.4. Dispersion of a broad pulse in steady, laminar axial flow in a tube. In the Taylor dispersion
problem, consider a distributed solute pulse of substance
A
introduced into a tube of length
L
containing a fluid in steady, laminar flow. Now the inlet boundary condition is that
with the same con~traints of negligible diffusion across the tube inlet and outlet as in Problem
20B.9. Note now that each element of solute acts independently of all the others.
(a) Using the result of Problem 20B.9, show that the exit concentration is given by
(b) Specialize this result for a square pulse:
f
=
fo
for 0
<
t
<
to;
f
=
0 for
t
>
to
(20D.4-3)
Sketch the result for several values of
(v,)t,/L.
20D.5. Velocity divergence in interfacially embedded coordinates. Consider a closed domain
D(u, w,
y)
in the interfacially embedded coordinates of Fig. 20.4-2.
(a) Integrate Eq. 20.4-7 over the boundary surface of
D
to obtain
in which
dS,
is a vector element of area, having magnitude
dS,
and the direction of the out-
ward normal to the boundary of the domain D.
(b) The integrand of the last term is the velocity of the boundary element
dSD.
Hence, the last
integral is the rate of change of the volume of D. Rewrite this integral accordingly with the
aid of Eq. 20.4-3, giving
The second equality is obtained by the Leibniz rule, noting that u,
w,
and
y
are independent
of
t
on each surface element
dSD.
(c)
Use the result of (b) and the Gauss-Ostrogradskii divergence theorem of
sA.5
to express
Eq.
20D.5-1 as the vanishing of a sum of three volume integrals over D(u,
w,
y).
Show that this
result, and the arbitrariness of the choice of D, yield
Eq.
20.4-8.
lo
R.
L.
Murray,
Nuclear Reactor Physics,
Prentice-Hall, Englewood Cliffs, N.J. (1957),
pp.
23,30,53.
