Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena
Подождите немного. Документ загружается.


g20.1 Time Dependent Diffusion
617
EXAMPLE
20.1-2
Gas Absorption with
Rapid
the heat of reaction removed through the solid. The concentration profile is a generalization
of that in Eq. 20.1-16:
n=
x,
-
x,,
- -
erf(Z
-
cp)
+
erf
cp
X~m
-
x~~
1
+
erf
cp
The dimensionless flux
cp
now depends on
XA,,
xAm, and the ratio N,,,/NAZ,:
1
(XAO
-
XA=)(NA~O
+
NB~o)
dII
cP=-
2 NAz0
-
x,,(Nh,
+
NB,)
*Z
Iz=,
(20.1 -24)
The relation between the interfacial fluxes and the terminal compositions is
(xAO
-
XA~)(NA~O
+
NB~o)
=
+
erf
cp)cp
exp
cp2
NA~O
-
XAO(NA~O
+
NB~o)
Equations 20.1-16,10, and 18 are included as special cases of the last three equations. The last
one is a
key
result for mass transfer calculations (see 522.8).
Gas
A
is absorbed by a stationary liquid solvent
S,
the latter containing solute
B.
Species
A
re-
acts with
B
in an instantaneous irreversible reaction according to the equation
aA
+
bB
+
Products. It may be assumed that Fick's second law adequately describes the diffusion
processes, since A,
B,
and the reaction products are present in
S
in low concentrations. Obtain
expressions for the concentration profiles.
Because of the instantaneous reaction of
A
and
B,
there will be a plane parallel to the
liquid-vapor interface at a distance
z,
from it, which separates the region containing no
A
from that containing no
B.
The distance
z,
is a function of t, since the boundary between A
and
B
retreats as
B
is used up in the chemical reaction.
The differential equations for c, and c, are then
dc~
d2cB
-
=
BBS
-
for
z,(t)
5
z
<
df
dz2
These are to be solved with the following initial and boundary conditions:
LC.: att
=
0,
CB
=
Cgm
forz
>
0
(20.1-28)
B.C. 1: at
z
=
0,
CA
=
C~~
(20.1-29)
B.C. 2,3: at
z
=
z,(f),
CA
=
cB
=
0 (20.1-30)
B.C.
4:
B.C.
5:
atz
=
m,
(20.1-32)
Here c,, is the interfacial concentration of
A,
and c,, is the original concentration of
B.
The
fourth boundary condition is the stoichiometric requirement that
a
moles of
A
consume
b
moles of
B
(see Problem 20B.2).
T.
K.
Sherwood,
R.
L.
Pigford, and
C.
R.
Wilke,
Absorption and Extraction,
3rd edition, McGraw-
Hill, New York (1975), Chapter 8. See also
G.
Astarita,
Mass Transfer with Chemical Reaction,
Elsevier,
Amsterdam (1967), Chapter
5.
For related problems with moving boundaries associated with phase changes, see
H.
S. Carslaw
and
J.
C.
Jaeger,
Conduction of Heat in Solids,
2nd edition, Oxford University Press (1959). See also
S.
G.
Bankoff,
Advances
in
Chemical Engineering,
Academic Press, New York (1964), Vol. 5, pp. 76-150;
J.
Crank,
Free and Moving Bounday Problems,
Oxford University Press (1984).

618
Chapter
20
Concentration Distributions with More Than One Independent Variable
The absence of a characteristic length in this problem, and the fact that c,
=
c,, both at
t
=
0 and z
=
w,
suggests trying a combination of variables. Comparison with the previous
example (without the
v:
term) suggests the following trial solutions:
c
A
--
Z
-
C,
+
C,erf-
for
0
I
z
5
zR(t)
CAO
v"GJ
C~
Z
-
=
C3
+
C4erf-
for zR(t)
5
z
<
CB~
V'qJ
These functions satisfy the differential equations, and if the constants of integration,
C1
to
C4,
can be so chosen that the initial and boundary conditions are satisfied, we will have the com-
plete solution to the problem.
Application of the initial condition and the first three boundary conditions permits the
evaluation of the integration constants in terms of zR(t), thereby giving
1
-
erf(~/V'49,~t)
for z&)
5
z
<
w
1
-
erf(zR/w)
B.C. 5 is then automatically satisfied. Finally, insertion of these solutions into
B.C.
4
gives the
following implicit equation from which zR(t) can be obtained:
Here
y
is a constant equal to z;/4t. Thus zR increases as
V%
To calculate the concentration profiles, one first solves Eq. 20.1-37 for
G,
and then in-
serts this value for
z,/fi
in Eqs. 20.1-35 and 36. Some calculated concentration profiles are
shown in Fig. 20.1-2 (for a
=
b),
to illustrate the rate of movement of the reaction zone.
From the concentration profiles we can calculate the rate of mass transfer at the interface:
Distance
from
interface
(mm)
Fig.
20.1-2.
Gas absorption with rapid chemical reaction, with concen-
tration profiles given by Eqs. 20.1-35 to 37 (for a
=
b).
This calculation
was made for
9,,
=
3.9
X
ft2/hr and
'3,,
=
1.95
X
lop5
fP/hr [T.
K.
Sherwood and
R.
L.
Pigford, Absorption and Extraction, McGraw-Hill,
New York (1952), p. 3361.

520.1 Time Dependent Diffusion
619
The average rate of absorption up to time
t
is then
Hence the average rate up to time
t
is just twice the instantaneous rate.
When species A diffuses in a liquid medium
B
and reacts with it irreversibly (A
+
B
+
C)
ac-
cording to a pseudo-first-order reaction, then the process of diffusion plus reaction is de-
Unsteady
Diffusion
scribed
by
with
First-Order
Homogeneous
~eaction~-~
SOLUTION
provided that the solution of
A
is dilute and that not much
C
is produced. Here
kr
is the rate
constant for the homogeneous reaction. Equation 20.1-40 is frequently encountered with the
initial and boundary conditions
and with a velocity profile independent of time. For such problems show that the solution is
Here
f
is the solution of Eqs. 20.1-40 to 42 with
k:
=
0
and
o,,
=
0, whereas
g
is the solution
with
ky
=
0 and
o,,
=
0.
This problem is linear in
o,.
It may, therefore, be solved by a superposition of two simpler
problems:
WA
=
02)
+
02)
(20.1-44)
with
wg'
described by the equations
j
P.
V.
Danckwerts,
Trans. Faraday Soc.,
47,1014-1023 (1951).
Peter Victor Danckwerts
(1916-1984)
was bomb disposal officer for the Port of London during "the
Blitz"
and was wounded in a mine field in
Italy during WWII; while teaching at Imperial College in London and at Cambridge University he
directed research on residence-time distribution, diffusion and chemical reaction, and the role of
diffusion in gas absorption.
A.
Giuliani and
F.
P.
Foraboschi,
Atti.
Acad. Sci.
Inst.
Bologna,
9,l-16 (1962);
F. P. Foraboschi,
ibid.,
11,l-14 (1964);
F.
P.
Foraboschi,
AlCkE
Journal,
11,752-768 (1965).
E.
N.
Lightfoot,
AIChE
Journal,
10,278-284 (1964).
".
E.
Stewart,
Ckem.
Eng.
Sci.,
23,483487 (1968);
corrigenda,
ibid.,
24,1189-1190 (1969).
There this
approach was generalized to time-dependent flows with homogeneous and heterogeneous first-order
reactions.

620
Chapter 20 Concentration Distributions with More Than One Independent Variable
and
wy)
described by
We now proceed to solve these two auxiliary problems by means of Laplace transform.
Taking the Laplace transform of the equations for
w$'
gives
P.D.E.
+
I.C.:
(p
+
k;")w2'
-
uAI(x, y,
Z)
+
i~
VW?))
=
9JABV
2-(1)
WA
(20.1-51)
-
B.C. at surfaces:
=
0
(20.1-52)
Now, the function
g
in Eq. 20.1-43 is the solution for
"2'
with
k;"
replaced by zero. Corre-
spondingly the Laplace transform satisfies Eqs. 20.1-51 and 52 with
p
+
k;"
replaced by
p:
Hence by taking $e inverse Laplace transform we get
which is the first part of the solution.
Next, taking the Laplace transform of Eqs. 20.1-48 to 50 gives
P.D.E.
+
I.C.:
(p
+
k;")Gz'
+
(V
'
VW~')
=
%ABV2Gg'
B.C. at surfaces: (20.1-56)
The Laplace transform
f
satisfies the same two equations with
k;"
replaced by zero. That
is,
if
we now use
s
for the transform variable in lieu of
p,
we have
P.D.E.
+
1.C.:
sj
+
(v
vf
)
=
GJABv2f
(20.1-57)
B.C. at surfaces:
-
1
f
=
s
~AO(XI
y,
2)
(20.1-58)
We see that the function
sf
satisfies the same boundary condition as p@ and that the differ-
ential equations for
sf
and
pWf)
are identical when
s
=
p
+
k"'.
Hence
Taking the inverse transform then gives
as the second part of the solution. Addition of the two parts of the solution,
wg'
and
my),
then
gives Eq. 20.1-43 directly.
Equation 20.1-43 provides a means for predicting concentration profiles in reacting sys-
tems from calculations or experiments on nonreacting systems at the same flow conditions.
Several extensions of this treatment are available, including multicomponent systems: turbu-
lent
and more general boundary
condition^.^-^
Y.-H.
Pao,
AIM
Journal,
2,1550-1559 (1964);
Ckem.
Eng.
Sci.,
19,694-696 (1964);
ibid.,
20,665469
(1965).
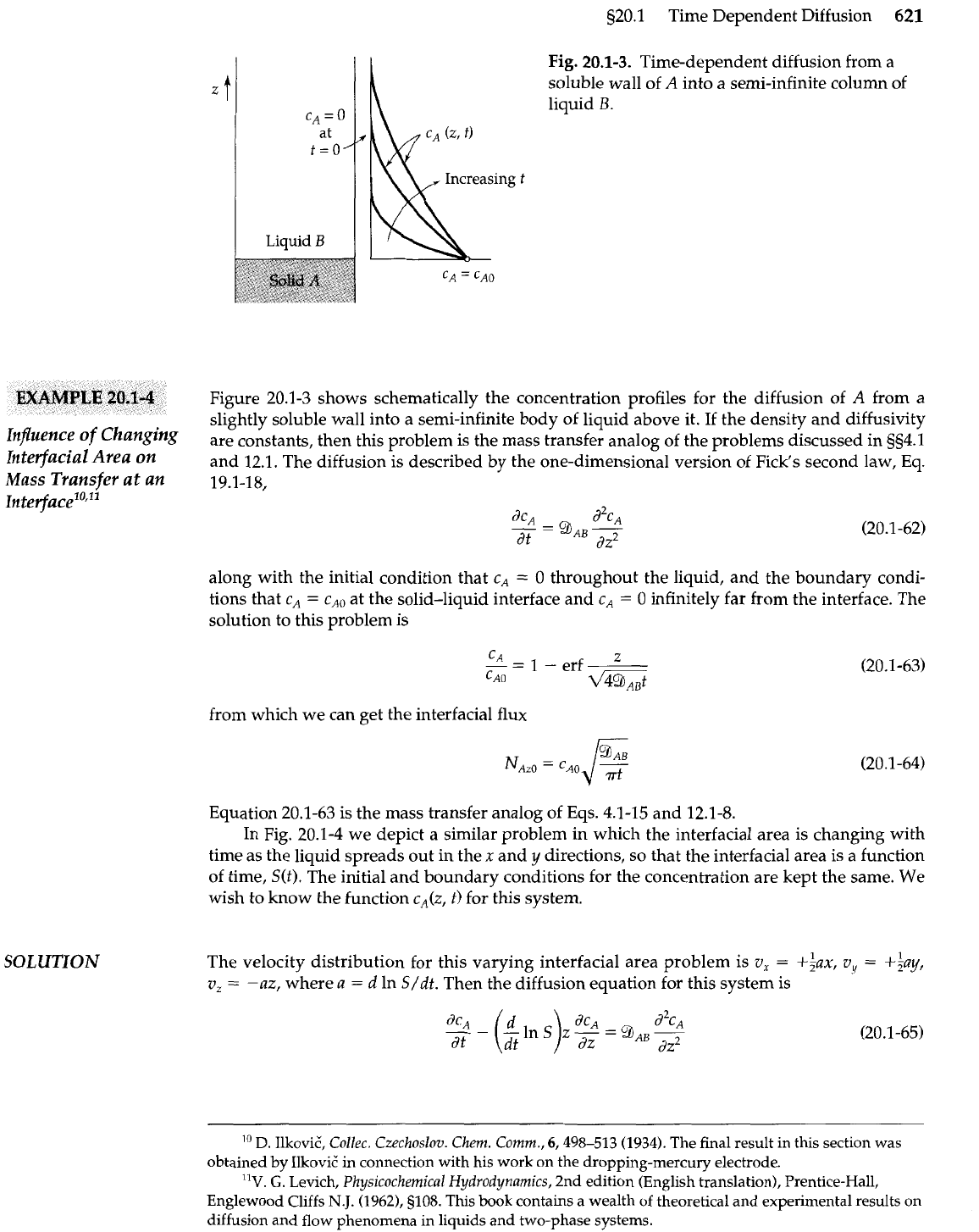
520.1 Time Dependent Diffusion
621
Fig.
20.1-3.
Time-dependent diffusion from a
soluble wall of
A
into a semi-infinite column of
liquid
B.
Figure 20.1-3 shows schematically the concentration profiles for the diffusion of
A
from a
slightly soluble wall into a semi-infinite body of liquid above it. If the density and diffusivity
Infruence
of
Changing
areconstants, then this problem is the mass transfer analog of the problems discussed in gg4.1
Interfacial Area on
and 12.1. The diffusion is described by the one-dimensional version of Fick's second law, Eq.
Mass Transfer at an 19.1-18,
~nterfacel~,"
SOLUTION
along with the initial condition that
cA
=
0
throughout the liquid, and the boundary condi-
tions that
cA
=
cA,
at the solid-liquid interface and
c,
=
0
infinitely far from the interface. The
solution to this problem is
from which we can get the interfacial flux
Equation 20.1-63 is the mass transfer analog of Eqs. 4.1-15 and 12.1-8.
In Fig. 20.1-4 we depict a similar problem in which the interfacial area is changing with
time as the liquid spreads out in the x and
y
directions, so that the interfacial area is a function
of time,
SO).
The initial and boundary conditions for the concentration are kept the same. We
wish to know the function cA(z,
t)
for this system.
The velocity distribution for this varying interfacial area problem is
v,
=
+$ax,
v,
=
+;fly,
v,
=
-az, where
a
=
d
In
S/dt.
Then the diffusion equation for this system is
'"
D.
Ilkovic',
Collec. Czechoslov. Chem. Comm.,
6,498-513 (1934). The final result in this section was
obtained by Ilkovit
in
connection with his work on the dropping-mercury electrode.
"V.
G.
Levich,
Physicochemical Hydrodynamics,
2nd edition (English translation), Prentice-Hall,
Englewood Cliffs
N.J.
(1962), $108. This book contains a wealth of theoretical and experimental results on
diffusion and flow phenomena in liquids and two-phase systems.

622
Chapter 20
Concentration Distributions with More Than One Independent Variable
Semi-infinite medium
in region
z
2
0.
The
mass transfer surface
S(t)
changes with time
/
Fig.
20.1-4.
Time-dependent diffusion across a mass transfer interface
S(t)
that is changing with time. The liquid
B,
in the region above the
plane
z
=
0, has a velocity distribution
v,
=
++ax,
v,
=
+$ay,
and
vZ
=
-az, where
a
=
d
In
S/dt.
7
Since Eq. 20.1-62 is solved by the method of combination of variables, the same technique can
be tried here. We postulate
'
A
Z
-
=
g(5)
with
5
=
--
'A,
80)
Substitution of this trial solution into Eq. 20.1-65 gives
If we set the expression within the brackets equal to unity, then we accomplish two things: (i)
we obtain an equation for
g
that has the same form as Eq. 4.1-9, to which the solution
is
known; (ii) we get an equation for
8
as a function of
t:
This equation may be integrated to give
The lower limit on the left side is chosen so as to ensure that
c,
=
0 initially throughout the
fluid. This choice then leads to
and we get finally for the concentration profiles
The interfacial mass flux is then obtained by differentiating Eq. 20.1-71 to get

520.2 Steady-State Transport in Binary Boundary Layers
623
The total number of moles of
A
that have crossed the interface at time
t
through the surface
S(t)
can be obtained from integration of
Eq.
20.1-71 as follows:
An equivalent expression can be obtained by integrating
Eq.
20.1-72:
Both Eq. 21.1-73 and Eq.
21.1-74
can be checked by verifying that
dMA/dt
=
N,,,(t)S(t).
If
S(t)
=
atn, where a is a constant, the above results simplify to
For the diffusion into the surrounding liquid from a gas bubble whose volume is increasing
linearly with time,
n
=
$
and
2n
+
1
=
g.
This is of course an approximate result, in which cur-
vature has been neglected, and is therefore valid only for short contact times. Related results
have been obtained for interfaces of arbitrary shapesr2,12 and experimentally verified for sev-
eral laminar and turbulent ~ysterns.~,'~
520.2
STEADY-STATE TRANSPORT
IN
BINARY BOUNDARY LAYERS
In
512.4
we discussed the application of boundary layer analysis to nonisothermal flow
of pure fluids. The equations of continuity, motion, and energy were presented in
boundary layer form and were solved for some simple situations. In this section we
ex-
tend the set of boundary layer equations to binary reacting mixtures, adding the equa-
tion of continuity for species
A
so that the concentration profiles can be evaluated. Then
we analyze three examples for the flat-plate geometry: one on forced convection with a
homogeneous reaction, one on rapid mass transfer, and one on analogies for small mass-
transfer rates.
"J.
B.
Angelo,
E.
N.
Lightfoot, and
D.
W.
Howard,
AKhE
Journal,
12,751-760 (1966).
l3
W.
E.
Stewart, in
Physicochemical Hydrodynamics
(D.
B.
Spalding, ed.), Advance Publications
Ltd.,
London, Vol.
I
(1977),
pp.
22-63.

624
Chapter
20
Concentration Distributions with More Than One Independent Variable
Consider the steady, two-dimensional flow of a binary fluid around a submerged ob-
ject, such as that in Fig. 4.4-1. In the vicinity of the solid surface, the equations of change
given in 5918.2 and 3 may be simplified as follows, provided that p,
p,
k,
ep,
and
9AB
are
essentially constant (except in the pg term), and that viscous dissipation can be neglected:
Continuity:
Motion:
Energy:
Continuity
of
A:
dv,
dv,
--
+
-
=
0
dx dy
The equation of ~ontinuity is the same as Eq. 12.4-1. The equation of motion, obtained
from Eq. 19.2-3, differs from Eq. 12.4-2 by the addition of the binary buoyant force term
%z(oA
-
oAm). The energy equation, obtained from Eq. (F) of Table 19.2-4, differs from
Eq. 12.4-3 by the addition of the chemical heat-source term -[(KIM,)
-
(%/~,)lr,.,.
Equation 20.2-4 is obtained from Eq. 19.1-16 by setting
oA
=
wA(x, y) and neglecting the
diffusion in the
x
direction. More complete equations, valid for high-velocity, variable-
property boundary layers, are available elsewhere.'
The usual boundary conditions on
v,
are that v,
=
0
at the solid surface, and
v,
=
v,(x)
at the outer edge of the velocity boundary layer. The usual boundary conditions on
T
in Eq. 20.2-3 are that
T
=
T,(x) at the solid surface, and
T
=
T,
at the outer edge of the
thermal boundary layer. The corresponding boundary conditions on
w,
in Eq. 20.2-4 are
that
o,
=
w,,(x)
at the surface and
o,
=
o,,
at the outer edge of the difusional boundary
layer. Thus there are now three boundary layers to consider, each with its own thickness.
In fluids with constant physical properties and large Prandtl and Schmidt numbers, the
thermal and diffusional boundary layers usually lie within the velocity boundary layer,
whereas for
Pr
<
1 and Sc
<
1 they may extend beyond it.
For mass transfer systems the velocity vy at the surface is usually not zero, but de-
pends on x. Hence we set vy
=
v,(x) at
y
=
0.
This boundary condition is appropriate when-
ever there is a net mass flux between the surface and the stream, as in melting, drying,
sublimation, combustion of the wall, or transpiration of the fluid through a porous wall.
Clearly, some of these processes are possible with pure fluids, but for simplicity we have
deferred their consideration to this chapter (see also 5918.3 and 22.8 for related analyses).
With the help of the equation of continuity, Eqs. 20.2-1 to 4 can be formally inte-
grated, with the boundary conditions just given, to obtain the following set of boundary
layer balances:
Continuity
+
motion:
Continuity
+
energy:
See, for
example,
W.
H.
Dorrance,
Viscous Hypersonic Flow,
McGraw-Hill,
New
York
(1962),
and
K.
Stewartson,
The Theory of Laminar Boundary Layers
in
Compressible
Fluids,
Oxford University Press
(1964).

5j20.2 Steady-State Transport in Binary Boundary Layers
625
Continuity
+
continuity of
A:
These equations are extensions of the
von
Ka'rmtin
balances
of
554.4
and
12.4
and may be
similarly applied, as shown in Example 20.2-1.
Boundary layer techniques have been of considerable value in developing the the-
ory of high-speed flight, separations processes, chemical reactors, and biological mass
transfer systems.
A
few of the interesting problems that have been studied are chemical
reactions in hypersonic boundary layers: mass transfer from dropletsI2 electrode polar-
ization in forced convection2 and free convection,3 reverse-osmosis water desalination:
and interphase transfer in packed-bed reactors and distillation c~lumns.~
EXAMPLE
20.2-1
Diffusion and Chemical
An appropriate mass transfer analog to the problem discussed in Example 12.4-1 would be
the flow along a flat plate that contains a species
A
slightly soluble in the fluid
B.
The concen-
tration at the plate surface would be c,,, the solubility
of
A
in
B,
and the concentration of
A
far
Ih~tion in Is~t~~~al
from the plate would be
cA,.
In this example we let c,,
=
0
and break the analogy with Exam-
Laminar Flow
Along
a
ple 12.4-1 by letting
A
react with
B
by an nth order homogeneous reaction, so that
RA
=
Soluble Flat Plate
-k,"'c;.
The concentration of dissolved
A
is assumed to be small, so that the physical proper-
ties
p,
p,
and
%,,
are virtually constant throughout the fluid. We wish to analyze the system,
sketched in Fig. 20.2-1, by the von KArmAn method.
SOLUTION
We begin by postulating forms for the velocity and concentration profiles. To minimize the
algebra and still illustrate the method, we select simple functions (clearly one can suggest
more realistic functions):
approaches with
~Z=O
velocity
/,8,(~)
71
Fig.
20.2-1.
Assumed velocity and con-
centration profiles for the laminar bound-
ary layer with homogeneous chemical
'
Concentration
C,O
reictibn.
V.
G.
Levich,
Physicochemical Hydrodynamics,
2nd edition (English translation), Prentice-Hall,
Englewood Cliffs,
N.J.
(1962).
C.
R.
Wilke, C. W. Tobias, and
M.
Eisenberg,
Chem.
Eng.
Prog.,
49,66-74 (1953).
W.
N.
Gill,
D.
Zeh, and
C.
Tien,
Ind. Eng. Chem. Fund.,
4,433439 (1965);
ibid.,
5,367-370 (1966).
See also
P.
L.
T.
Brian,
ibid.,
4,439445 (1965).
J.
P.
Sdrensen and W.
E.
Stewart,
Chem. Eng.
Sci.,
29,833-837 (1974);
W.
E.
Stewart and
D.
L.
Weidman,
ibid.,
45,2155-2160 (1990);
T.
C.
Young and W.
E.
Stewart,
AIChE
Journal,
38,592-602,
1302 (1992).

626
Chapter 20 Concentration Distributions with More Than One Independent Variable
Note that we use different thicknesses, 6 and a,, for the velocity and concentration boundary
layers. In order to relate this problem to that of Example 12.4-1, we introduce the quantity
A
=
6J6, which in this case is a function of
x
because of the chemical reaction occurring. We
restrict the discussion to
A
5
1, for which the concentration boundary layer lies entirely
within the velocity boundary layer. We can also neglect the interfacial velocity
vo
=
v,l,=,,
which is small here because of the small solubility of
A.
Insertion of these expressions into
Eqs. 20.2-5 and
7
then gives the differential equations
for the boundary layer thicknesses
6
and 6,
=
SA.
Equation 20.2-10
is
readily integrated to give
I
Insertion of this regult into Eq. 20.2-11 and multiplication by -6A/vc,, gives
as the differential equation for
A.
Thus
A
depends on the Schmidt number, Sc
=
p/pQAB, and
on the dimensionless position coordinate shown in the square brackets. The bracketed quan-
tity is 1 /(n
+
1)
times the first Damkohler number6 based on the distance
x.
When no reaction is occurring,
ky
is zero, and
Eq.
20.2-13 becomes a linear first-order reac-
tion for
A3.
When that equation is integrated, we get
in which
C
is a constant of integration. Because
A
does not become infinite as
x
--+
0, we obtain
in the absence of chemical reaction (cf. Eq. 12.4-15):
That is, when there is no reaction and Sc
>
1,
the concentration and velocity boundary layer
thicknesses bear a constant ratio to one another, dependent only on the value of the Schmidt
number.
When a
slow
reaction occurs (or when
x
is small), a series solution to
Eq.
20.2-13 can be ob-
tained:
A
=
SC~'/~(~
+
a,t
+
a2t2
+
.
.
a)
in which
Substitution of this expression into
Eq.
20.2-13 gives
Because a, is negative, the concentration boundary layer thickness is diminished by the chem-
ical reaction.
G.
Damkohler,
Zeits.
f.
Electrochemie,
42,846-862
(1936);
W.
E.
Stewart,
Chem.
Eng.
Prog.
Symp.
Series,
#58,
61,16-27
(1965).
