Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena

Подождите немного. Документ загружается.

519.4 Use of the Equations of Change for Mixtures

597

SOLUTION

Fig.

19.4-3.

Three-compo-

Outer edge of

nent system with a catalytic

stagnant gas film

consisting

chemical reaction.

For this analysis, the reaction is assumed to occur instantaneously and irreversibly at the cat-

alytic surface. The gas composition at the outer edge of the film (at

is presumed

known, and the catalyst surface is at

The temperature and pressure are assumed to be

independent of position throughout the film. We label the chemical species by: O2

co2

For steady-state, one-dimensional diffusion without homogeneous reactions, Eq. 19.1-10 gives

which tells us that all of the molar fluxes are constants across the film. From boundary condi-

tions provided by the stoichiometry of the problem we further know that

The Maxwell-Stefan equations of Eq. 17.9-1 then give:

These equations have been simplified by using Eq. 19.4-32, and by using the fact that

9,,

over

wide range of temperature. The latter may be seen by using Appendix

to show that

a,,

3.793A and

a,,

3.714A, and that

E~~/K

145K and

E,,/K

146K.

Since only the mole fraction

appears in

Eq.

19.4-33, this equation may be integrated6 at

once to give

-2

(x,

exp

(

2:)

Combination of the last two equations then gives, after integration

N3zz

)

xI0

x30)

exp

[-(2

913

I)(%)] (19-4-36)

(x,,

2) exp

2~91,

Three-component problems with two diffusivities equal have been discussed by

Toor,

AIChE

Journal,

3,198-207 (1957).

598

Chapter

Equations of Change for Multicomponent Systems

EXAMPLE

19.4-4

Thermal Conductivity

Polyatomic Gas

SOLUTION

From this equation and a similar one for

x2,

we can get

Then from Eq.

19.4-35

we get

which gives the rate of production of carbon dioxide at the catalytic surface. This result can

then be substituted into Eqs.

19.4-35

and

and the three mole fractions can be calculated as

functions of

59.3

we pointed out that the thermal conductivities of polyatomic gases deviate from the

formula for monatomic gases, because of the effects of the internal degrees of freedom in the

complex molecules. When the Eucken formula for polyatomic gases (Eq.

9.3-15)

is divided

the formula for monatomic gases (Eq.

9.3-14)

and use is made of the ideal gas law, one can

write the ratio of the polyatomic gas thermal conductivity to that of a monatomic gas as

Derive a result of this form by modeling the polyatomic gas as an interacting gas mixture, in

which the various "species" are the polyatomic gas molecules in the various rotational and vi-

brational states.

The heat flux for

gas mixture is given in Eq.

19.3-3.

All "species" will have the same thermal

conductivity because they differ only in their internal quantum states. Therefore we expect

each

to be

Lon.

Similarly, the mass flux for each "species" should be given by Fick's law

for

a pure gas

-pB,,Vw,,

with all the

a,,

having a common value

9,,,.

Thus we get

since the molecular weights of all the "species" are the same.

If now it is postulated that the distribution over the various quantum states is in equilib-

rium with the local temperature, then

Vx,

(dx,/dT)VT.

Then we can define the

effective ther-

mal

conductivity

of the mixture by

and write

kp0ly

-1+

kon

=1+

Here the temperature-dependent quantity

can be calculated from the kinetic theory of gases at low density. It varies ogly very slowly

with temperature, and a suitable mean value is

1.106.

The quantity

~p,poIy

dH/dT

is the heat

capacity for a gas in which the equilibrium among the various quantum states is maintained

519.5

Dimensional Analysis of the Equations of Change for Nonreacting Binary Mixtures

599

during the change of temperature, whereas

Cp,m,,

is the heat capacity for a gas in which tran-

sitions between quantum states are not allowed, so that

C,,,,,

$R.

When the numerical

value

1.106 is inserted in

Eq.

19.4-41, we get finally

which is the formula recommended by Hir~chfelder.~ Although the predictions of Eq. 19.4-43

are not much better than those of the older Eucken formula, the above development does at

least give some feel for the role of the internal degrees of freedom in heat cond~ction.~,~

519.5

DIMENSIONAL ANALYSIS OF THE EQUATIONS OF

CHANGE FOR NONREACTING BINARY MIXTURES

In this section we dimensionally analyze the equations of change summarized in 519.2,

using special cases of the flux expressions of 919.3. The discussion parallels that of 511.5

and serves analogous purposes: to identify the controlling dimensionless parameters of

representative mass transfer problems, and to provide an introduction to the mass trans-

fer correlations of Chapter 22.

Once again we restrict the discussion primarily to systems of constant physical

properties. The equation of continuity for the mixture then takes the familiar form

Continuity:

(19.5-1)

The equation of motion may be approximated in the manner of Boussinesq (see g11.3) by

putting Eqs. 19.3-2 and 19-5.1 into

Eq.

19.2-3, and replacing

-Vp

-V9.

For a

constant-viscosity Newtonian fluid this gives

Motion:

The energy equation, in the absence of chemical reactions, viscous dissipation, and exter-

nal forces other than gravity, is obtained from Eq. (F) of Table 19.2-4, with Eq. 19.3-3. In

using the latter we further neglect the diffusional transport of energy relative to the mass

average velocity. For constant thermal conductivity this leads to

Energy:

in which

k/p?,,

is the thermal diffusivity. For nonreacting binary mixtures with con-

stant

and

B,,,

Eq. 19.1-14 takes the form

Continuity of

For the assumptions that have been made, the analogy between Eqs. 19.5-3 and 4 is clear.

Hirschfelder,

Chem.

Phys.,

26,274-281 (1957); see also

Secrest and

Hirschfelder,

Physics of

Fluids,

4,61-73 (1961) for further development of the theory, in wluch equilibrium among the

various quantum states is not assumed.

For a comparison

the two formulas with experimental data, see Reid, Prausnitz, and Poling,

op. cit.,

497. The Hirschfelder formula in Eq.

19.4-42

and the Eucken formula of Eq. 9.3-15 tend to

bracket the observed conductivity values.

Ferziger and H.

Kaper,

Mathematical

Theory

of Transport Processes in Gases,

North Holland,

Amsterdam (1977), g511.2 and

600

Chapter 19 Equations of Change for Multicomponent Systems

We now introduce the reference quantities

I,,

v,, and Yo, used

93.7 and 911.5, the

reference temperatures

and

of 511.5, and the analogous reference mass fractions

o,,

and w,,. Then the dimensionless quantities we will use are

Here it is understood that

is the mass average velocity of the mixture. It should be

recognized that for some problems other choices of dimensionless variables may be

preferable.

In terms of the dimensionless variables listed above, the equations of change may be

expressed as

Continuity:

i;)

0 (1 9.5-8)

Motion:

Energy:

Continuity of

RePr

DGA

v2&A

ReSc

The Reynolds, Prandtl, and thermal Grashof numbers have been given in Table 11.5-1.

The other two numbers are new:

1-1

Schmidt number

Gr,

[gi(w~l

mAu)C]

diffusional Grashof number

The Schmidt number is the ratio of momentum diffusivity to mass diffusivity and repre-

sents the relative ease of molecular momentum and mass transfer. It is analogous to the

Prandtl number, which represents the ratio of the momentum diffusivity to the thermal

diffusivity. The diffusional Grashof number arises because of the buoyant force caused

by the concentration inhomogeneities. The products RePr and ReSc in Eqs. 19.5-10 and 11

are known as Pkclet numbers, Pk and PkAB, respectively.

The dimensional analysis of mass transfer problems parallels that for heat transfer

problems. We illustrate the technique by three examples: (i) The strong similarity be-

tween Eqs. 19.5-10 and 11 permits the solution of many mass transfer problems by anal-

ogy with previously solved heat transfer problems; such an analogy is used in Example

19.5-1. (ii) Frequently the transfer of mass requires or releases energy, so that the heat

and mass transfer must be considered simultaneously, as is illustrated in Example 19.5-2.

(iii) Sometimes, as in many industrial mixing operations, diffusion plays a subordinate

role in mass transfer and need not be given detailed consideration; this situation is illus-

trated in Example 19.5-3.

We shall see then that, just as for heat transfer, the use of dimensional analysis for

the solution of practical mass transfer problems is an art. This technique is normally

most useful when the effects of at least some of the many dimensionless ratios can be ne-

glected. Estimation of the relative importance of pertinent dimensionless groups nor-

mally requires considerable experience.

519.5

Dimensional Analysis of the Equations of Change for Nonreacting Binary Mixtures

601

We wish to predict the concentration distribution about a long isothermal cylinder of a

volatile solid

immersed in a gaseous stream of a species

which is insoluble in solid

Concentration

The system is similar to that pictured in Fig. 11.5-1, except that here we consider the transfer

Distribution about a

of mass rather than heat. The vapor pressure of the solid is small compared to the total pres-

Long Cylinder

sure in the gas, so that the mass transfer system is virtually isothermal.

Can the results of Example 11.5-1 be used to make the desired prediction?

SOLUTION

The results of Example 11.5-1 are applicable if it can be shown that suitably defined dimen-

sionless concentration profiles in the mass transfer system are identical to the temperature

profiles in the heat transfer system:

ijA(X,

ij,

f(X,

ij,

(19.5-14)

This equality will be realized if the differential equations and boundary conditions for the

two systems can be put into identical form.

We therefore begin by choosing the same reference length, velocity, and pressure as in

Example 11.5-1, and an analogous composition function:

ij,

(w,

w~~)/(o~~

~~~1. Here

w,,

is the mass fraction of

in the gas adjacent to ths interface, and

wAco

is the value far from

the cylinder. We also specify that

w,,

so that

The equations of change needed

here are then Eqs. 19.5-8,9, and 11. Thus the differential equations here and in Problem 11.5-1

are analogous except for the viscous heating term in Eq. 11.5-3.

As for the boundary conditions, we have here:

B.C.

1: as

ij2

tix

1 (19.5-15)

B.C.

at f2

ij2

(wA0

@Am)

v=-

Vij,

ijA

(19.5-16)

ReSc (I

wA0)

The boundary condition on

obtained with the help of Fick's first law, states that there is an

interfacial radial velocity resulting from the sublimation of

If we compare the above description with that for heat transfer in Example 11.5-1, we see

that there is no mass transfer counterpart of the viscous dissipation term in the energy equa-

tion and no heat transfer counterpart to the interfacial radial velocity component in the

boundary condition of

Eq.

19.5-16. The descriptions are otherwise analogous, however, with

G,,

Sc, and Gr, taking the places of

Pr, and Gr.

When the Brinkman number is sufficiently small, viscous dissipation will be unimpor-

tant, and that term in the energy equation can be neglected. Neglecting the Brinkman number

term is appropriate, except for flows of very viscous fluids with large velocity gradients, or in

hypersonic boundary layers (510.4). Similarly, when (l/ReSc)[(w,,

wA,)/(l

wAo)l

is very

small, it may be set equal to zero without introducing appreciable error. If these limiting con-

ditions are met, analogous behavior will be obtained for heat and mass transfer. More pre-

cisely, the dimensionless concentration

will have the same dependence on

q,Z,

Re, Pr,

and Gr, as the dimensionless temperature

will have on f,

jl,

Re, Pr, and Gr. The concen-

tration and temperature profiles will then be identical at a given Re whenever Sc

Pr and

Gr,

Gr.

The thermal Grashof number can, at least in principle, be varied at will by changing To

T,.

Hence it is likely that the desired Grashof numbers can be obtained. However, it can be

seen from Tables 9.1-1 and 17.1-1 that Schmidt numbers for gases can vary over a considerably

wide range than can the Prandtl numbers. Hence it may be difficult to obtain a satisfactory

thermal model of the mass transfer process, except in a limited range of the Schmidt number.

Another possibly serious obstacle to achieving similar heat and mass transfer behavior is

the possible nonuniformity of the surface temperature. The heat of sublimation must be ob-

tained from the surrounding gas, and this in turn will cause the solid temperature to become

lower than that of the gas. Hence it is necessary to consider both heat and mass transfer si-

multaneously. A very simple analysis of simultaneous heat and mass transfer is discussed in

the next example.

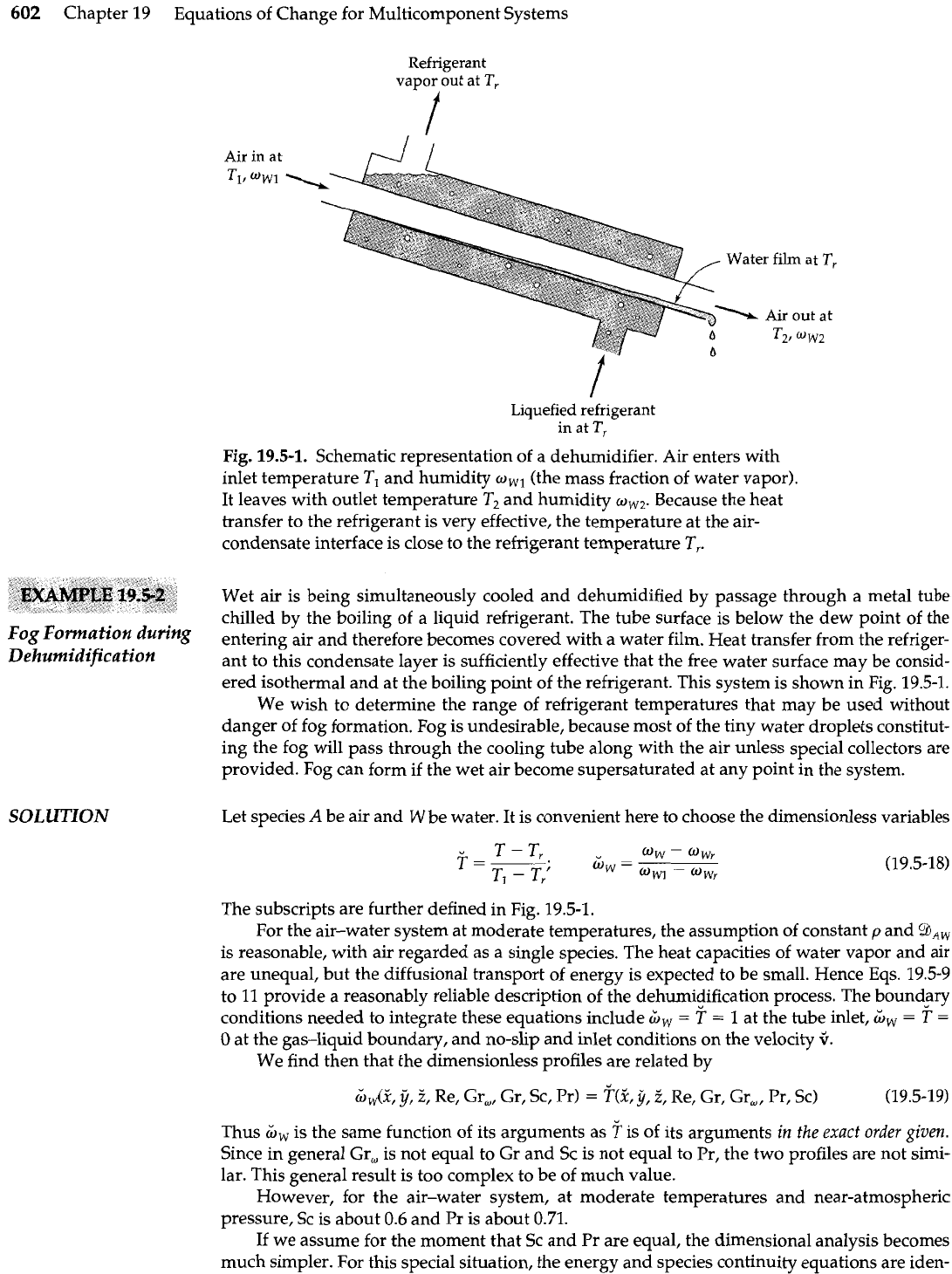
602

Chapter 19 Equations of Change for Multicomponent Systems

EXAMPLE

19.5-2

Fog Formation during

Dehumidification

SOLUTION

Refrigerant

vapor

out

Air in

Liquefied refrigerant

Fig.

19.5-1.

Schematic representation of a dehumidifier. Air enters with

inlet temperature

and humidity

owl

(the mass fraction of water vapor).

It leaves with outlet temperature

and humidity

ow,

Because the heat

transfer to the refrigerant

very effective, the temperature at the air-

condensate interface is close to the refrigerant temperature

T,.

Wet air is being simultaneously cooled and dehumidified by passage through a metal tube

chilled by the boiling of a liquid refrigerant. The tube surface is below the dew point of the

entering air and therefore becomes covered with a water film. Heat transfer from the refriger-

ant to this condensate layer is sufficiently effective that the free water surface may be consid-

ered isothermal and at the boiling point of the refrigerant. This system is shown in Fig. 19.5-1.

We wish to determine the range of refrigerant temperatures that may be used without

danger of fog formation. Fog is undesirable, because most of the tiny water droplets constitut-

ing the fog will pass through the cooling tube along with the air unless special collectors are

provided. Fog can form if the wet air become supersaturated at any point in the system.

Let species

be air and

be water. It is convenient here to choose the dimensionless variables

The subscripts are further defined in Fig. 19.5-1.

For the air-water system at moderate temperatures, the assumption of constant

and

BAW

is reasonable, with air regarded as a single species. The heat capacities of water vapor and air

are unequal, but the diffusional transport of energy is expected to be small. Hence Eqs. 19.5-9

provide a reasonably reliable description of the dehumidification process. The boundary

conditions needed to integrate these equations include

at the tube inlet,

at the gas-liquid boundary, and no-slip and inlet conditions on the velocity

We find then that the dimensionless profiles are related by

ijw(f,

Re, Gr,, Gr, Sc, Pr)

?(?,

ij,

Re, Gr, Gr,, Pr, Sc)

(19.5-19)

Thus

ZiW

is the same function of its arguments as

is of its arguments

the

exact

order

given.

Since in general Gr, is not equal to Gr and Sc is not equal to Pr, the two profiles are not simi-

lar. This general result is too complex to be of much value.

However, for the air-water system, at moderate temperatures and near-atmospheric

pressure, Sc is about

0.6

and Pr is about 0.71.

If we assume for the moment that Sc and Pr are equal, the dimensional analysis becomes

much simpler. For this special situation, the energy and species continuity equations are iden-

g19.5

Dimensional Analysis of the Equations of Change for Nonreacting Binary Mixtures

603

Fig.

19.5-2.

representative dehumidifica-

tion path. The dehumidification path

shown here corresponds to T,,,,,, the low-

est refrigerant temperature ensuring the

absence of fog. The dehumidification path

for this situation is a tangent to the satura-

tion curve through the point

(w,,,

T,), rep-

resenting the given inlet-air conditions.

Calculated dehumidification paths for

lower refrigerant temperatures would

cross the saturation curve. Saturation water

vapor concentrations would then be ex-

ceeded, making fog formation possible.

Temperature,

tration and temperature profiles are then identical. It should be noted that equality of Gr, and

Gr is not required. This is because the Grashof numbers affect the concentration and tempera-

ture profiles only by way of the velocity

which appears in both the continuity equation and

the energy equation in the same way.

Therefore, with the assumption that Sc

Pr, we have

at each point

the system. This means, in turn, that

evey

concentration-temperature pair in

the tube lies on a straight line between

(owl,

Tl) and (ow,

T,)

on a psychrometric chart. This is

shown graphically in Fig. 19.5-2 for

representative set of conditions. Note that

(w,,.,

Tr) must

lie on the saturation curve, since equilibrium is very closely approximated.

It follows that there can be no fog formation if a straight line drawn between

(w,,

TI)

and

(w,,,

T,) does not cross the saturation curve. Then the lowest refrigerant temperature that

cannot produce fog is represented by the point of tangency of a straight line through

(ow,

TI)

with the saturation curve.

It should be noted that

all

of the conditions along the line from the inlet

(ow,,

TI) to

(w,,

T,) will occur in the gas even though the bulk or cup-mixing conditions vary only from

(w,,

TI) to

(o,,

T,). Thus some fog can form even if saturation is not reached in the bulk of the

flowing gas. For air entering at 90°F and 50% relative humidity, the minimum safe refrigerant

temperature is about 45°F. It may also be seen from Fig. 19.5-2 that it is not necessary to bring

all of the wet air to its dew point in order to dehumidify it. It is only necessary that the air be

saturated at the cooling surface. The exit bulk conditions

(w,,

T,) can be anywhere along the

dehumidification path between

(w,,

TI)

and (w,,

TJ,

depending on the effectiveness of the

apparatus used. Calculations based on the assumed equality of Sc and Pr have proven very

useful for the air-water system.

In addition, it can be seen, by considering the physical significance of the Schmidt and

Prandtl numbers, that the above-outlined calculation procedure is conservative. Since the

Schmidt number is slightly smaller than the Prandtl number, dehumidification will proceed

proportionally faster than cooling, and concentration-temperature pairs will lie slightly

below the dehumidification path drawn in Fig. 19.5-2. In condensing organic vapors from air,

the reverse situation often occurs. Then the Schmidt numbers tend to be higher than the

Prandtl numbers, and cooling proceeds faster than condensation. Conditions then lie above

the straight line of Fig. 19.5-2, and the danger of fog formation is increased.

604

Chapter 19 Equations of Change for Multicomponent Systems

Fig.

19.5-3.

Blending of miscible fluids. At zero time, the

upper half of this tank is solute free, and the lower half

contains

uniform distribution of solute at a dimen-

sionless concentration of unity, and the fluid is motion-

less. The impeller is caused to turn at a constant rate of

rotation

for all time greater than zero. Positions in the

z=-

tank are given by the coordinates

with

measured

radially from the impeller axis, and

upward from the

bottom of the tank.

Develop by dimensional analysis the general form of a correlation for the time required to

blend two miscible fluids in an agitated tank. Consider a tank of the type described in Fig.

19.5-3, and assume that the two fluids and their mixtures have essentially the same physical

Fluids

properties.

SOLUTION

It will be assumed that the achievement of "equal degrees of blending" in any two mixing op-

erations means obtaining the same dimensionless concentration profile in each. That is, the

dimensionless solute concentration

is the same function of suitable dimensionless coordi-

nates

(?,

0,i)

of the two systems when the degrees of blending are equal. These concentration

profiles will depend on suitably defined dimensionless groups appearing

the pertinent

conservation equations and their boundary conditions, and on a dimensionless time.

In this problem we select the following definitions for the dimensionless variables:

Here D is the impeller diameter,

is the rate of rotation of the impeller in revolutions per

unit time, and

is the prevailing atmospheric pressure. The dimensionless pressure

is used

here rather than the quantity

defined in

53.7;

the formulation with

is simpler and gives

equivalent results. Note that

is equal to the total number of turns of the impeller since the

start of mixing.

The conservation equations describing this system are Eqs. 19.5-8, 9, and

with zero

Grashof numbers. The dimensionless groups arising in these equations are Re, Fr, and Sc. The

boundary conditions include the vanishing of

on the tank wall and of

on the free liquid

surface. In addition we have to specify the initial conditions

1H H

atf 50, &,=O for--<?<-

20 D

(19.5-22)

att 50, 1 forO<i<--

(19.5-23)

and the requirement of no slip on the impeller (see Eq.

3.7-34).

We find then that the concentration profiles are functions of Re, Sc, Fr, the dimensionless

time

the tank geometry (via H/D and B/D), and the relative proportions of the two fluids.

That is,

(Re, Fr, Sc,

geometry, initial conditions)

(19.5-25)

It is frequently possible to reduce the number of variables to be investigated.

Questions for Discussion

605

It has been observed that, if the tank is properly baffled,' no vortices of importance occur;

that is, the free liquid surface is effectively level. Under these circumstances, or in the absence

of a free liquid surface, the Froude number does not appear in the system description, as we

found in

53.7.

It is further found, in most operations on low-viscosity liquids, that the rate-limiting step

is the creation of a finely divided dispersion of one fluid in the other. In such a dispersion, the

diffusional processes take place over very small distances. As a result, molecular diffusion is

not rate limiting, and the Schmidt number (Sc) has little importance. It is further found that

the effect of the Reynolds number (Re) is negligible under most commonly encountered con-

ditions. This is because most of the mixing takes place in the interior of the tank where vis-

cous effects are small, rather than in the boundary layers adjacent to the tank and impeIler

surfaces, where they are large.'

For most impeller-tank combinations in common use, the Reynolds number (Re) is

unimportant when its value is above about lo4. This behavior has been substantiated by a

number of

investigator^.^

We thus arrive,

after extensive experimentation,

at a surprisingly simple result. When all of

the assumptions above are valid, the concentration profile depends only on

Hence

the di-

mensionless time required to produce any desired degree of mixing is

constant

for a given system

geometry. In other words, the total number of turns of the impeller during the mixing process

determines the degree of blending, independently of Re, Fr, Sc, and tank size-provided, of

course, that the tanks and impellers are geometrically similar.

For the same reasons,

a properly baffled tank, the dimensionless velocity distribution

and the volumetric pumping efficiency of the impeller are nearly independent of the Froude

number (Fr) and of the Reynolds number (Re), when Re

lo4.

QUESTIONS FOR DISCUSSION

How do the various equations of change given in Chapters

and 11 have to be modified for

reacting mixtures?

What modifications in the flux expressions given in Chapters 3 and

are needed to describe

chemically reacting mixtures?

Under what conditions is

v")

Equations 19.1-24 and

are physically equivalent. For what kinds of problems is there a

preference for one form over the other?

Interpret physically each term in the equations in Table 19.2-3.

The thermal conductivity of a mixture is defined as the ratio of the heat flux to the negative of

the temperature gradient when all the diffusional mass fluxes are zero. Interpret this state-

ment in terms of Eq. 19.3-3.

common and effective baffling arrangement for vertical cylindrical tanks with axially mounted

impellers is a set of four evenly spaced strips along the tank wall, with their flat surfaces in planes

through the tank axis, extending from the top to the bottom of the tank and at least two-tenths of the

distance to the tank center.

The insensitivity of the required mixing time to the Reynolds number can

seen intuitively from

the fact that the term

(l/~e)?%

Eq.

19.5-9

becomes small compared to the acceleration term

LX/DZ

large Re. Such intuitive arguments are dangerous, however, and the effect of Re is always important in

the immediate neighborhood of solid surfaces. Here the amount of mixing taking place in the immediate

neighborhood of solid surfaces is small and can

neglected.

The insensitivity of the required mixing time to the Schmidt number can be seen from the time-

averaged equation of continuity in Chapter

21.

At large Re, the turbulent mass flux is much greater than

that due to molecular diffusion, except in the immediate neighborhood of the solid surfaces.

Fox and

Gex,

AlChE

Journal,

2,539-544 (1956);

Kramers,

Baars, and

Knoll,

Chem.

Eng

Sci, 2,3542 (1955);

van de Vusse,

Chem.

Eng.

Sci., 4,178-200,209-220 (1955).

606

Chapter 19 Equations of Change for Multicomponent Systems

Discuss the similarities and differences between heat transfer and mass transfer.

Go through all the steps

converting Eq. 19.3-4 into Eq. 19.3-6. Why is the latter (approxi-

mate) result important?

Comment on the statement at the end of Example 19.4-1 that the rate of heat transfer is di-

rectly affected by simultaneous mass transfer, whereas the reverse is not true.

PROBLEMS

19A.1.

Dehumidification of air (Fig. 19.4-1). For the system of Example 19.4-1, let the vapor be

H,O

and the stagnant gas be air. Assume the following conditions (which are representative in

air

conditioning): (i) at

80°F and

XHzo

0.018; (ii) at

50°F.

(a) For

atm, calculate the right side of Eq. 19.4-9.

(b) Compare the conductive and diffusive heat flux at

0. What is the physical significance

of your answer?

Answer:

(a) 1.004

19B.1.

Steady-state evaporation (Fig. 18.2-1). Rework the problem solved in 518.2, dealing with the

evaporation of liquid

into gas

starting from Eq. 19.1-17.

(a) First obtain an expression for

v*,

using Eq.

(M)

of Table 17.8-1, as well as Fick's law in the

form of Eq.

(D)

of Table 17.8-2.

(b) Show that

Eq.

19.1-17 then becomes the following nonlinear second-order differential

equation:

(c)

Solve this equation to get the mole fraction profile given in Eq. 18.2-11.

19B.2.

Gas absorption with chemical reaction (Fig. 18.4-1). Rework the problem solved in 518.4,

starting with Eq. 19.1-16. What assumptions do you have to make in order to get Eq. 18.4-4?

19B.3.

Concentration-dependent diffusivity. A stationary liquid layer of

is bounded by planes

0 (a solid wall) and

(a gas-liquid interface). At these planes the concentration of

is cAo and

CAb

respectively. The diffusivity

9AB

is a function of the concentration of

(a) Starting from Eq. 19.1-5 derive a differential equation for the steady-state concentration

distribution.

(b) Show that the concentration distribution is given by

(c)

Show that the molar flux at the solid-liquid surface is

(dl Now assume that the diffusivity can be expressed as a Taylor series in the concentration

in which

+(cAo

c,)

and

gA,

QAB(CA). Then, show that

(e) How does this result simplify if the diffusivity is a linear function of the concentration?