Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena

Подождите немного. Документ загружается.

520.2 Steady-State Transport in Binary Boundary Layers

627

When a fast reaction occurs (or when

is very large), a series solution in I/( is more ap-

propriate. For large t, we assume that the dominant term is of the form

const.

where

0. Substitution of this trial function into Eq. 20.2-13 then shows that

(sc@-~/~

for large

(20.2-19)

Combination of Eqs. 20.2-12 and 19 shows that, at large distances from the leading edge,

the concentration boundary layer thickness

becomes a constant independent of

and

Once

A@,

Sc) is known, then the concentration profiles and the mass transfer rate at

the surface may be found.

more refined treatment of this problem has been given else-

where.7

The laminar boundary layer on

flat plate (see Fig. 20.2-2) has been a popular system for heat

and mass transfer studies. In this example, we give an analysis of subsonic forced convection

Forced

Convection

from

in this geometry at high mass-transfer rates, and discuss the analogies that hold in this situa-

Flat Plate

High

tion. This example is an extension of Example

4.4-2.

Mass-Transfer Rates

SOLUTION

Consider the nonisothermal, steady, tyo-dimensional flow of

binary fluid in the system of

Fig. 20.2-2. The fluid properties

C,,

and

9,+,

are considered constant, viscous dissipa-

tion is neglected, and there are no homogeneous chemical reactions. The Prandtl boundary

layer equations for the laminar region are

Continuity:

Motion:

Energy:

Continuity of

dv,

d2vx

v,--+v

-=v-

dy dy2

Outer flow:

11,

Transition

11,

1 region

11,

Line

constant

Fig.

20.2-2.

TangentiaI flow along a

sharp-edged semi-infinite flat plate

with mass transfer into the stream.

The laminar-turbulent transition

IIT

usually occurs at a length Reynolds

Leading edge

11,

number

(xv,/v),,,,

on the order of

'The

boundary layer below

the

plate

omitted here

lo5

to lo6.

Chambre and

Young,

Physics

Fluids,

1,48-54 (1958). Catalytic surface reactions in

boundary layers have been studied

Chambr6 and A. Acrivos,

Appl.

Pkys.,

27,1322-1328

(1956).

628

Chapter 20

Concentration Distributions with More Than One Independent Variable

The boundary conditions are taken to be:

Here the function vO(x) stands for

V&X,

evaluated at

0 and describes the distribution

mass transfer rate along the surface. This function will be specified later.

Equation 20.2-20 can be integrated, with the boundary condition of Eq. 20.2-26, to give

This expression isto be inserted for v, into Eqs. 20.2-21 to 23.

To capitalize on the analogous form of Eqs. 20.2-21 to 23 and the first six boundary condi-

tions, we define the dimensionless profiles

and the dimensionless physical property ratios

With these definitions, and the above equation for

v,,

Eqs. 20.2-21 to 23 all take the form

and the boundary conditions on the dependent variables reduce to the following:

Thus the dimensionless velocity, temperature, and composition profiles all satisfy the same

equation, but with their individual values of

The form of the boundary conditions on

suggests that a combination of variables be

tried. By analogy with

Eq.

4.4-20 we select the combination:

Then by treating

and

as functions of

(see Problem 20B.3), we obtain the differential

equation

with the boundary conditions

520.2 Steady-State Transport in Binary Boundary Layers

629

From the last three equations we conclude that the profiles will be expressible in terms of the

single coordinate q, if and only if the interfacial velocity vo(x) is of the form

Any other functional form for

v,(x)

would cause the left side of Eq. 20.2-34 to depend on both

x and q,

that a combination of variables would not be possible. The boundary layer equa-

tions would then require integration in two dimensions, and the calculations would become

more difficult. Equation 20.2-37 specifies that vo(x) vary as

1/fi,

and thus, inversely with the

boundary layer thickness

of Eq. 4.4-17.This equation has the same range of validity as Eq.

20.2-34, that is,

(v,x/v)

(v,x/v),,,

(see Fig. 20.2-2).

Fortunately the condition in Eq. 20.3-37 is a useful one. It corresponds to a direct propor-

tionality of pv, to the interfacial fluxes

70,

qO,

and

jAO.

Conditions of this type arise naturally in

diffusion-controlled surface reactions, and also in certain cases of drying and transpiration

cooling. The determination of

for these situations is considered at the end of this example.

Until then we treat

as given.

With the specification of v,(x) according to Eq. 20.2-37, the problem statement is com-

plete, and we are ready to discuss the calculation of the profiles. This is best done by numeri-

cal integration, with specified values of the parameters

and

The first step in the solution is to evaluate the velocity profile ll,. For this purpose it is

convenient to introduce the function

which is a generalization of the dimensionless stream function

used in Example 4.4-2. Then

setting

in Eq. 20.2-34 and making the substitutions

df/dq

II,,

d2f/dV2

dII,/dv, and so on, gives the equation of motion in the form

and Eqs. 20.2-35,36, and 38 give the boundary conditions

Equation 20.2-39 can be solved numerically with these boundary conditions to obtain

as a

function of q for various values of

Once the function f(q,

has been evaluated, we can integrate

Eq.

20.2-34 with the

boundary conditions in Eqs. 20.2-35 and 36 to obtain

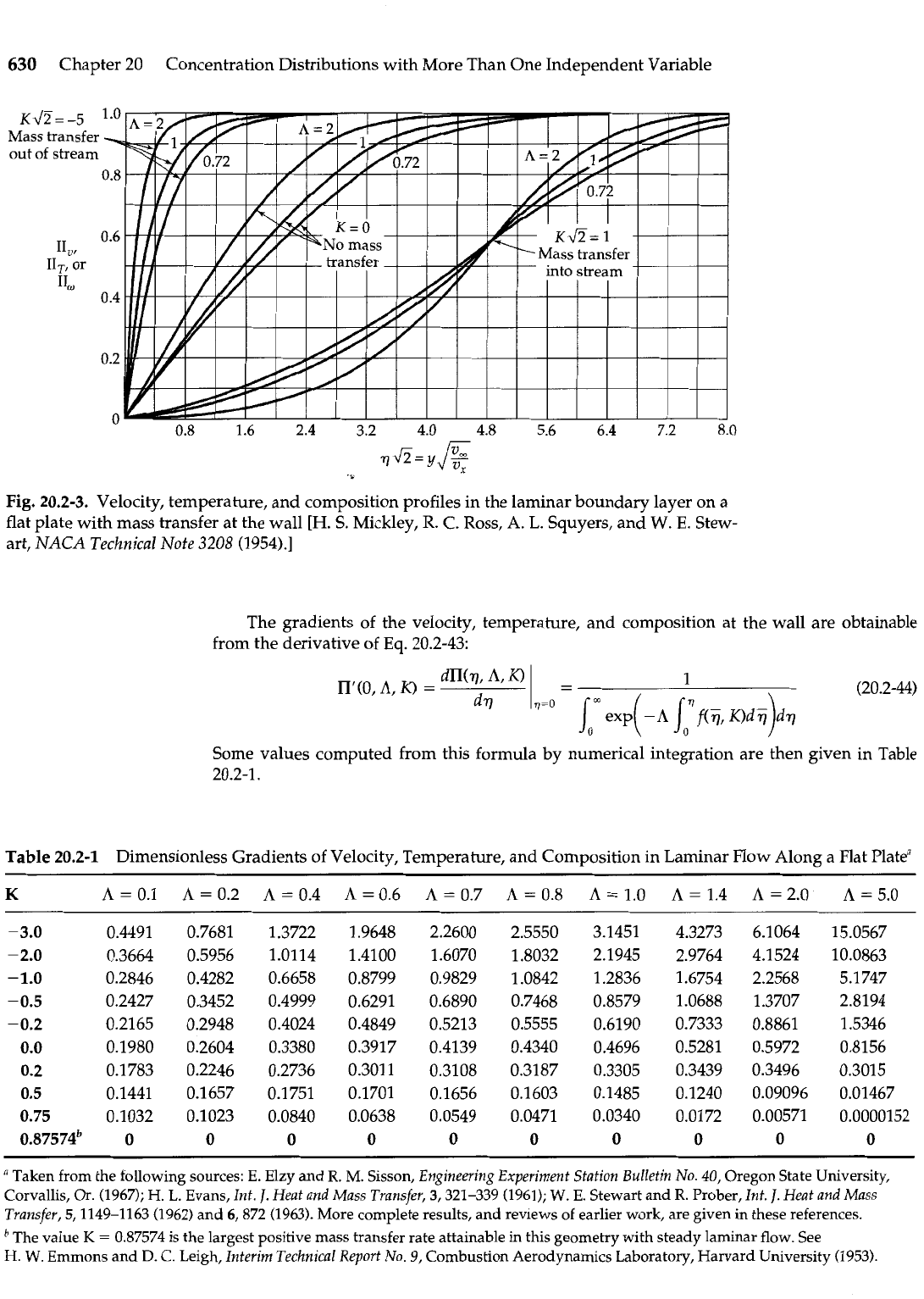
Some profiles calculated from this equation by numerical integration are given in Fig. 20.2-

3. The velocity profiles are given by the curves for

The temperature and composition

profiles for various Prandtl and Schmidt numbers are given by the curves for the corre-

sponding values of

Note that the velocity, temperature, and composition boundary lay-

ers get thicker when

is positive (as in evaporation) and thinner when

is negative (as in

condensation).

630

Chapter 20 Concentration Distributions with More Than One Independent Variable

Fig.

20.2-3.

Velocity, temperature, and composition profiles in the laminar boundary layer on a

flat plate with mass transfer at the wall

[H.

Mickley,

Ross, A.

Squyers, and

Stew-

art,

NACA

Technical

Note

3208

(1954).1

The gradients of the velocity, temperature, and composition at the wall are obtainable

from the derivative of

Eq.

20.2-43:

Some values computed from this formula by numerical integration are then given in Table

20.2-1.

Table

20.2-1

Dimensionless Gradients of Velocity, Temperature, and Composition in Laminar Flow Along a Flat Plate"

Taken from the following sources: E. Elzy and

Sisson,

Engineering Experiment Station Bulletin

No.

40,

Oregon State University,

Corvallis, Or. (1967);

Evans,

Int.

Heat and Mass Transfer,

3,321-339 (1961);

E. Stewart and

Prober,

Int.

Heat and Mass

Transfer,

5,1149-1163 (1962) and 6,872 (1963). More complete results, and reviews of earlier work, are given in these references.

The value

0.87574 is the largest positive mass transfer rate attainable in this geometry with steady laminar flow. See

Emmons and

C. Leigh,

Interim Technical Report

No.

Combustion Aerodynamics Laboratory, Harvard University (1953).

s20.2 Steady-State Transport in Binary Boundary Layers

631

The molecular fluxes of momentum, energy, and mass at the wall are then given by the

dimensionless expressions

with the tabulated values of lI'(0, A,

K).

Thus the fluxes can be computed directly when

is known. These expressions are obtained from the flux expressions of Newton, Fourier,

and Fick, and the profiles as given in Eq. 20.2-43. The energy flux

here corresponds to

the conduction term -kVT of Eq. 19.3-3; the diffusive flux j,, is obtained by using Eq. 20.2-47

above.

The fluid properties

ep,

and

PA,

have been treated as constants in this develop

ment. However, Eqs. 20.2-45 to 47 have been found to agree closely with the corresponding

variable-property

calculation^,^'^

provided that

is generalized as follows,

and that p,

k, and

are evaluated at the "reference conditions"

:(T,

T.)

and

UA~

$bAO

@Am).

In many situations, one of the following dimensionless quantities

is known or readily computed. These flux ratios, R, are independent of

under the present

boundary conditions and are related to A and

as follows,

according to Eqs. 20.2-45 to

51.

From Eq. 20.2-52 we see that the dimensionless interfacial

mass flux

can be tabulated as a function of

and A, by use of the results in Table 20.2-1.

Then

can be found by interpolation if the numerical values of R and A are given for one of

the three profiles (i.e., if we can specify

R,,

or R, and Pr, or R, and Sc.) Convenient plots of

these relations are given

Figures 22.8-5 to

As a simple illustration, suppose that the flat plate is porous and is saturated with liquid

A, which vaporizes into a gaseous stream of

and

Suppose also that gas

is noncondens-

able and insoluble in liquid A, and that

wAo

and

o,,

are given. Then R, can be calculated from

For calculations of momentum and energy transfer in gas flows with

see

Eckert,

Trans.

A.S.M.E.,

78,1273-1283 (1956).

For calculations of momentum and mass transfer in binary and multicomponent gas mixtures, see

Stewart and

Prober,

Ind.

Eng.

Chem.

Fundamentals,

3,224-235 (1964);

improved reference

conditions are provided

Young and

Stewart,

ibid.,

25,276482 (19861,

as noted in

922.9.

For other methods of applying

Eq.

20.2-47

to variable-property fluids, see

Hanna,

AIChE

Joltrnnl,

8,278-279 (1962); 11,706-712 (1965).

632

Chapter

Concentration Distributions with More Than One Independent Variable

Table

20.2-2

Coefficients for the Approximate Flat-Plate Formulas," Eqs.

20.2-54

and

Taken

from

Merk,

Appl.

Sci.

Res.,

A8,237-277 (1959),

and

Prober and

Stewart,

Int.

Heat and Mass Transfer,

6,221-229,

Eq.

20.2-51

with

and

can be found by ihterpolating the function

K(R, A)

and

p/pQAB.

For moderate values of

the calculations can be simplified by representing II'(0,

as a truncated Taylor series in the parameter

This expansion can be written more compactly as

in which

and

are slowly varying functions of

given in Table

20.2-2.

Insertion of

Eq.

20.2-54

into Eq.

20.2-52

gives the convenient expression for the dimensionless interfa-

cial mass flux

for calculations with unknown parameter

This result is easy to use and fairly accurate. The

predicted function

K(R,

is within

1.6%

of that found from Table 20.2-1 for

(R(

0.25

and

0.1.

This example illustrates the related effects of the interfacial velocity v, on the velocity,

temperature, and composition profiles. The effect of

on a given profile,

II,

is small if

for that profile (as in most separation processes) and large if

(as in many combustion

and transpiration cooling processes). Some applications are given in Chapter

22.

EXAMPLE

20.2-3

Approximate Analogies

for the Flat Plate at

Low Mass-Transfer

Rates

Pohlhausen" solved the energy equation for the system of Example

12.1-2

and curve-fitted

his results for the heat transfer rate Q (see third line of Table

12.4-1).

Compare his result with

Eq.

20.2-46,

and derive the corresponding results for the momentum and mass fluxes.

SOLUTION

By inserting the coefficient

0.664

in place of

v148/315

in Eq.

12.4-17,

and setting 2Wqo(x)

(dQldL)I,,,, we get

This result is subject to the boundary condition v,,(x)

which corresponds to

0 in the

system of Example

20.2-2.

Pohlhausen,

Zeits.

angew. Math. Mech.,

1,115-121 (1921).

520.3 Steady-State Boundary Layer Theory for Flow Around Objects

633

Equation 20.2-56 is obtainable from Eq. 20.2-46 when

0 by setting IIf(O, Pr, 0)

0.4696~r"~; this agrees with Table 20.2-2 at

Making comparable substitutions in Eqs.

20.2-45 and 46, we get the convenient analogy

which has been recommended by Chilton and Colburn12 for this flow situation (cf. 5514.3 and

22.3). The expression for agrees with the exact solution at

0, and the results for

and

j,,

are accurate within

22%

=O for

0.5.

520.3

STEADY-STATE BOUNDARY LAYER THEORY

FOR FLOW AROUND OBJECTS

In 9518.5 and

we discussed two related mass transfer problems of boundary layer type.

Now we want to enlarge'-7 on the ideas presented there and consider the flow around

objects of other shapes such as the one shown in Fig. 12.4-2. Although we present the

material in this section in terms of mass transfer, it is understood that the results can be

taken over directly for the analogous heat transfer problem by appropriate changes of

notation. The concentration boundary layer is presumed to be very thin, which means

that the results are restricted either to small diffusivity or to short exposure times. The

results are applicable only to the region between the forward stagnation locus (from

which

is measured) and the region of separation or turbulence, if any, as indicated in

Figure 12.4-2.

The concentration of the diffusing species is called c,, and its concentration at the

surface of the object is c,,. Outside the concentration boundary layer, the concentration

is zero.

Proceeding as in Example 12.4-3, we adopt an orthogonal coordinate system for the

concentration boundary layer, in which

is measured along the surface everywhere in

the direction of the streamlines. The y-coordinate is perpendicular to the surface, and the

z-coordinate is measured along the surface perpendicular to the streamlines. These are

"general orthogonal coordinates," as described in Eqs. A.7-10 to 18, but with

1, and

hx(x,

and

h,(x,

z).

Since the flow near the interface does not have

velocity

component in the

direction, the equation of continuity there is

H. Chilton and

Colburn,

Ind. Eng. Chem.,

26,1183-1187 (1934).

A. Acrivos,

Chem. Eng. Sci.,

17,457-465 (1962).

Stewart,

AKhE Journal,

9,528-535 (1963).

Howard and

N. Lightfoot,

AlChE lournal,

14,458-467 (1968).

Stewart,

Angelo, and

Lightfoot,

AlChE Journal,

16,771-786 (1970).

Lightfoot, in

Lecfures in Transport Phenomena,

American Institute of Chemical Engineers, New

York

(1969).

Ruckenstein,

Chem. Eng. Sci.,

23,363-371 (1968).

Stewart, in

Physicochemical Hydrodynamics,

Vol.

1 (D.

Spalding, ed.), Advance

Publications, Ltd., London

(1977),

pp.

22-63.

634

Chapter 20

Concentration Distributions with More Than One Independent Variable

according to Eq. A.7-16. The diffusion equation for the concentration boundary layer is then

where Eqs. A.7-15 and 17 have been used. In writing these equations it has been as-

sumed that: (i) the x- and z-components of the diffusion flux are negligible, (ii) the

boundary layer thickness is small compared to the local interfacial radii of curvature,

and (iii) the density and diffusivity are constant. We now want to get formal expressions

for the concentration profiles and mass fluxes for two cases that are generalizations of

the problems solved in 518.5 and 518.6. When we get the expressions for the local molar

flux at the interface, we will find that the dependences on the diffusivity ($power in

518.5 and the $-power in 918.6) correspond to cases (a) and

(b)

below. This turns out to be

of great importance in the establishment of dimensionless correlations for mass transfer

coefficients, as we shall see in Chapter 22.

Zero Velocity Gradient at the Mass Transfer Surface

This situation ariges in a surfactant-free liquid flowing around a gas bubble. Here

does

not depend on y, and

can be obtained from the equation of continuity given above.

Therefore, for small mass-transfer rates we can write general expressions for the velocity

components as

v,(x,

(20.3-3)

where

depends on

and z. When this is used in Eq. 20.3-2, we get for the diffusion

the liquid phase

which is to be solved with the boundary conditions

B.C. 1:

B.C. 2:

B.C. 3:

The nature of the boundary conditions suggests that a combination of variables treatment

might

appropriate. However, it is far from obvious how to construct an appropriate

di-

mensionless combination. Hence we

try

the following: let cA/cA0

fir)),

where

y/6,(x, z),

and 6,(x,

is the boundary layer thickness for species

to be determined later.

When the indicated combination of variables is introduced into Eq. 20.3-5, the equa-

tion becomes

with the boundary conditions: f(0)

1 and f(w)

0. If, now, the coefficient of the

r)(df/dr)) term were a constant, then Eq. 20.3-9 would have the same form as Eq. 4.1-9,

which we know how to solve. For convenience we specify the constant as

Next we insert the expression for

from Eq. 20.3-4 and rearrange the equation thus:

920.3 Steady-State Boundary Layer Theory for Flow Around Objects

635

Linear Velocity Profi

This is a linear, first-order equation for 6:, which has to be solved with the boundary

condition 6,

0 at x

0. Integration of Eq. 20.3-11 gives

as the thickness function for the diffusional boundary layer. Since Eq. 20-3-9 and the bound-

ary conditions then contain

as the only independent variable, the postulated combination

of variables is valid, and the concentration profiles are given by the solution of Eq. 20.3-9:

f(7)

exp

(-7')

dTj

erfq

Equations 20.3-12 and 13 are the solution to the problem at hand.

Next, we combine this solution with Fick's first law to evaluate the molar flux of

species

at the interface:

This result shows the same dependence of the mass flux on the .$power of the diffusivity

that arose in Eq. 18.5-17, for the much simpler gas absorption problem solved there. In

fact, if we set the scale factors

and

equal to unity and replace v, by v,,,, we recover

Eq. 18.5-17 exactly.

.le Near

the

Mass-Transfer Surface

This velocity function is appropriate for mass transfer at a solid surface (see Example

12.4-3) when the concentration boundary layer is very thin. Here v, depends linearly on

within the concentration boundary layer, and vy can be obtained from the equation of

continuity. Consequently, when the net mass flux through the interface is small, the ve-

locity components in the concentration boundary layer are

in which

depends on

and z. Substituting these expressions into Eq. 20.3-2 gives the

diffusion equation for the liquid phase

which is to be solved with the boundary conditions

B.C. 1:

B.C. 2:

B.C. 3:

atx

aty

C~o

asy+m, cA+O

Once again, we use the method of combination of variables, by setting cA/cA0

f(q),

where

y/SA(x, z).

When the change of variables is made, the diffusion equation becomes

636

Chapter 20 Concentration Distributions with More Than One Independent Variable

EXAMPLE

20.3-1

Mass Transfer for

Creeping Flow Around

Gas Bubble

with the boundary conditions: f(0)

and f(m)

solution of the form f(q) is possi-

ble only if the factor in parentheses is

constant. Setting the constant equal to

reduces

Eq. 20.3-21 to Eq. 18.6-6, for which the solution is known. Therefore we now get the

boundary layer thickness by requiring that

The solution of this first-order, linear equation for

Hence the solution to the problem in this subsection is

/vmexp (-ij3) dij

f(q)

C~~

which reduces to Eq. 18.6-10 for the system considered there.

Finally, we get the expression for the molar flux at the interface, which is

For a plane surface, with

and

constant, Eq. 20.3-26 reduces to

Eq.

18.6-11.

liquid

is flowing very slowly around a spherical bubble of gas

of radius R. Find the rate

of mass transfer of

into the surrounding fluid, if the solubility of gas

in liquid

c~,.

(a)

Show how to use Eq. 20.3-14

get the mass flux at the gas-liquid interface for this system.

(b)

Then get the average mass flux over the entire spherical surface.

SOLUTION

(a)

Select as the origin of coordinates the upstream stagnation point, and define the coordi-

nates

and

as follows:

RO and

R(sin 8)4, in which

and

are the usual spherical

coordinates. The

direction is then the same as the

direction of spherical coordinates.

The

interfacial velocity is obtained from Eq. 4B.3-3 as

iv,

sin 8, where v, is the approach

velocity.

When these quantities are inserted into

Eq.

20.3-14

we get

(R sin 13)~(iv, sin 8)'

(R)(R sin 8)2(:v, sin 8)d(R8)