Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena

Подождите немного. Документ загружается.

519.2 Summary of the Multicomponent Equations of Change

587

Table

19.2-1

Equations of Change for Multicomponent Mixtures in Terms of

the Combined Fluxes

Mass

pw,

-(V

nu)

1,2,

...,A9

Momentum:

-[V.+]

(A)"

(Eq. 19.1-6)

Energy:

d-'

Zp(u

:v2)

-(V.e)

(pv-g)

(CIb

(Eq. 11.1-6)

When all

equations of continuity are added, the equation of continuity for the fluid

mixture

is obtained. Here

is the mass average velocity defined in Eq.

17.7-1.

If species

is acted on by a force per unit volume given by

then

has to be

replaced by

X,p,g,

Eq.

(B),

and

(pv

has to be replaced by

ZJn,

g,)

Eq.

(C).

These replacements are required, for example, if some of the species are ions with

different charges on them, acted on by an electric field. Problems of this sort are

discussed in Chapter

24.

evolved by experience and experiment and therefore are generally accepted by the scien-

tific community.'

The three "combined fluxes," which appear in Eqs.

(A)

(C)

of Table 19.2-1, can be

written as the

convective fluxes

plus the

molecular

(or

diffusive) fluxes.

These various fluxes

are displayed in Table 19.2-2, where the equation numbers corresponding to their first

appearance are given.

When the flux expressions of Table 19.2-2 are substituted into the conservation

equations of Table 19.2-1 and then converted to the

D/Dt

form by means

Eqs. 3.5-4

and

we get the multicomponent equations of change in their usual forms. These are

tabulated in Table 19.2-3.

In addition to these conservation equations, one needs also to have the expressions

for the fluxes in terms of the gradients and the transport properties (the latter being func-

tions of temperature, density, and composition). Finally one nceds Aalso the thermal

equation of state,

p(p,

x,),

and the caloric equation of state,

U(p,

x,),

and in-

formation about the rates of any homogeneous chemical reactions occurring2

Actually the conservation laws for energy, momentum, and angular momentum follow from

Lagrange's equation of motion, together with the homogeneity of time, the homogeneity of space, and

the isotropy of space, respectively

(Noether's

theorem).

Thus there is something very fundamental about

these conservation laws, more than is apparent at first sight. For more on this, see

Landau and

Lifshitz,

Mechanics,

Addison-Wesley, Reading, Mass.

(1960),

Chapter

and Emrny Noether,

Nachr.

Kgl.

Ges.

Wiss.

Gottingen

(Math.-phys.

Kl.)

(19181,

pp.

235-257.

Amalie

Emmy

Noether

(1882-1935),

after

doing the doctorate at the University of Erlangen, was a protkgke of Hilbert in Gottingen until Hitler's

purge of

1933

forced her to move to the United States, where she became a professor of mathematics at

Bryn Mawr College; a crater on the moon is named after her.

One might wonder whether or not we need separate equations of motion and energy for species

Such equations can be derived by continuum arguments, but the species momentum and energy fluxes

are not measurable quantities and molecular theory is required in order to clarify their meanings.

These separate species equations are not needed for solving transport problems. However, the

species equations of motion have been helpful for deriving kinetic expressions for the mass fluxes

in multicomponent systems [see

Curtiss and

B. Bird,

Proc.

Nut.

Acad.

Sci.

USA,

93,7440-7445

(1996)

and

Chem. Phys., 111,10362-10370 (199911.

588

Chapter 19 Equations of Change for Multicomponent Systems

Table 19.2-2 The Combined, Molecular, and Convective Fluxes for

Multicomponent Mixtures (all with the same sign convention)

Combined

Molecular

Convective

Entity flux flux flux

Mass

PV"a (AY

(a=

1,2,

...,A0

(Eq. 17.8-1)

Momentum

(Eq. 1.7-1)

Energy e

q+[msv1

pv(b+$v2) (CY

(Eq. 9.8-5)

The velocity

appearing in all these expressions is the mass average velocity, defined in

Eq.

17.7-1.

The molecular momentum flux consists of two parts:

The molecular energy flux is made up of the heat flux vector

and the work flux vector

v],

the latter occurring only in flow systems.

Table 19.2-3

Equations of Change for Multicomponent Mixtures in Terms of

the Molecular Fluxes

Total mass:

-p(V

(A)

(Eq. (A) of Table 3.5-1)

Species mass:

Dm'?

PDt

-(V.j,)

1,2,...,N)

(BY

(Eq. 19.1-7a)

Momentum:

-Vp

[V-T]

(Ob

(Eq.

(B)

of Table 3.5-1)

Energy:

)

-(V

pv)

17.

v])

(pv

(D)~

(Eq.

(El of Table 11.4-1)

Only N

of these equations are independent, since the sum of the

equations gives

See note

(b)

of Table

19.2-1

for the modifications needed when the various species are

acted on by different forces.

We conclude this discussion with a few remarks about special forms of the equa-

tions of motion and energy. In 511.3 it was pointed out that the equation of motion as pre-

sented in Chapter

is in suitable form for setting up forced-convection problems, but

that an alternate form

(Eq.

11.3-2) is desirable for displaying explicitly the buoyant forces

resulting from temperature inequalities in the system. In binary systems with concentra-

tion inequalities as well as temperature inequalities, we write the equation of motion as

in Eq.

(B)

of Table

3.5-1

and use an approximate equation of state formed by making

double Taylor expansion of p(T,

w,)

about the state

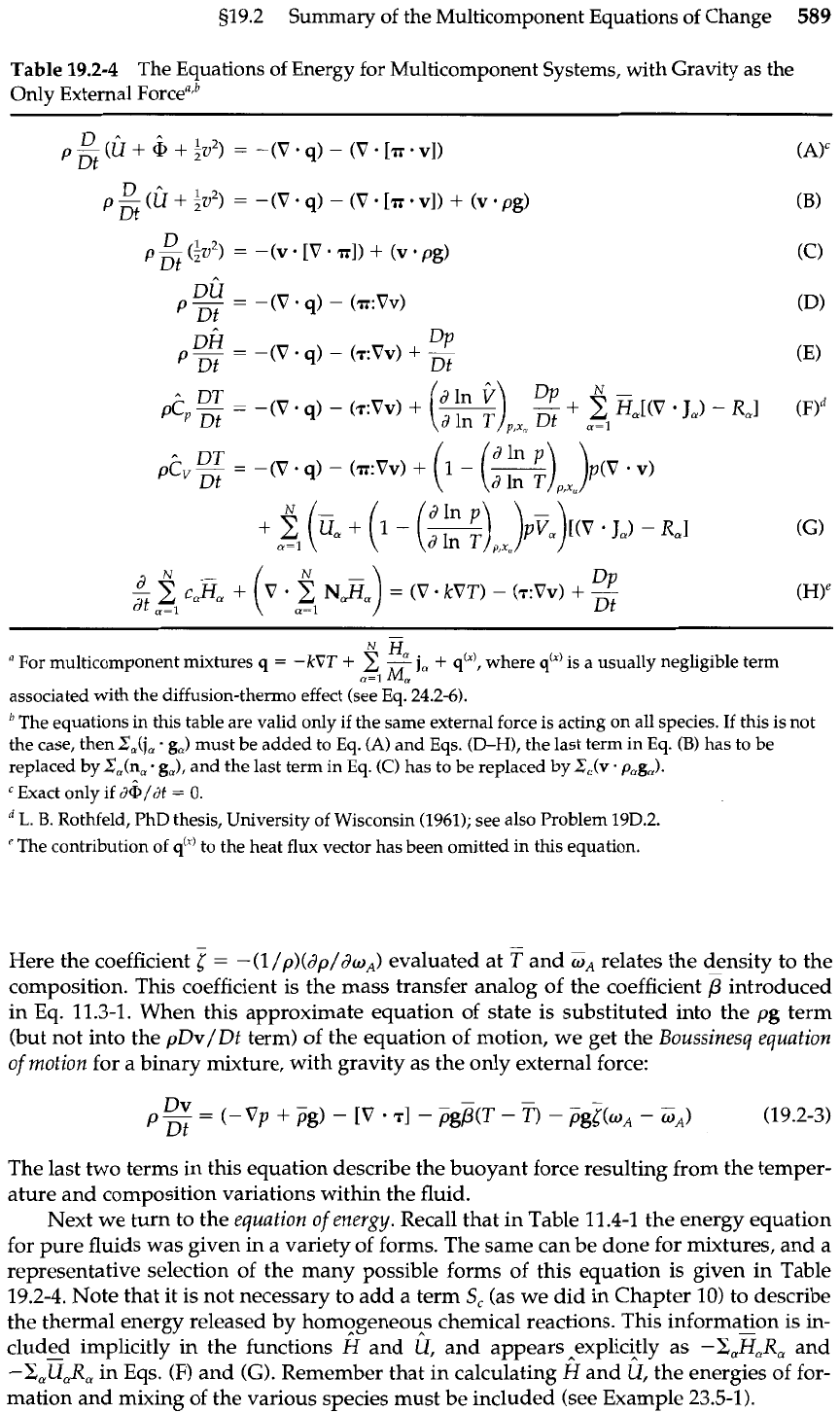
519.2

Summary of the Multicomponent Equations of Change

589

Table

19.2-4

The Equations of Energy for Multicomponent Systems, with Gravity as the

Only External Forcearb

For multicomponent mixtures

-kVT

q'"',

where

q'"

is a usually negligible term

w=l

associated with the diffusion-thermo effect (see Eq. 24.2-6).

The equations

this table are valid only if the same external force is acting on all species. If this is not

the case, then

ZJj,

g,) must be added to Eq.

(A)

and Eqs.

(D-H),

the last term in Eq.

(B)

has to be

replaced byZ,(n,

. g,),

and the last term in Eq.

(C)

has to be replaced by

Z,(v.

page).

Txact only if

d&/dt

Rothfeld, PhD thesis, University of Wisconsin (1961); see also Problem 19D.2.

'The contribution of

q"'

to the heat

flux

vector has been omitted in this equation.

Here the coefficient

-(l

/p)(dp/doA) evaluated at

and

relates the density to the

composition. This coefficient is the mass transfer analog of the coefficient

introduced

in Eq. 11.3-1. When this approximate equation of state is substituted into the pg term

(but not into the pDv/Dt term) of the equation of motion, we get the

Boussinesq equation

of motion

for a binary mixture, with gravity as the only external force:

The last two terms in this equation describe the buoyant force resulting from the temper-

ature and composition variations within the fluid.

Next we turn to the

equation of energy.

Recall that in Table 11.4-1 the energy equation

for pure fluids was given in a variety of forms. The same can be done for mixtures, and a

representative selection of the many possible forms of this equation is given in Table

19.2-4. Note that it is not necessary to add a term

(as we did in Chapter 10) to describe

the thermal energy released by homogeneous chemical reactions. This information is in-

cluded implicitly in the functions

and

and appears explicitly as

-xaEa~,

and

-X,U,R,

in Eqs.

(F)

and

(G).

Remember that in calculating

and

fi/

the energies of for-

mation and mixing of the various species must be included (see Example 23.5-1).

590

Chapter 19 Equations of Change for Multicomponent Systems

519.3

SUMMARY OF THE MULTICOMPONENT

FLUXES

The equations of change have been given in terms of the fluxes of mass, momentum, and

energy. To solve these equations, we have to replace the fluxes by expressions involving

the transport properties and the gradients of concentration, velocity, and temperature.

Here we summarize the flux expressions for mixtures:

Mass:

-p9ARV~A binary only

Momentum:

-,u[Vv

(vv)~]

($,u

K)(V

v)S

Energy:

Now we append a few words of explanation:

The mass flux expression given here is for binary mixtures only. For multicom-

ponent gas mixtures at moderate pressures, we can use the Maxwell-Stefan

equations of Eq. 17.9-1. There are additional contributions to the mass flux cor-

responding to driving forces other than the concentration gradients: forced difu-

sion, which occurs when the various species are subjected to different external

forces; pressure diffusion, proportional to Vp; and thermal diffusion, proportional

to VT. These other diffusion mechanisms, the first two of which can be quite

important, are covered in Chapter

24.

The momentum flux expression is the same for multicomponent mixtures as for

pure fluids. Once again we point out that the contribution containing the dilata-

tional viscosity

is seldom important. Of course, for polymers and other vis-

coelastic fluids, Eq. 19.3-2 has to be replaced by more complex models, as

explained in Chapter

The energy-flux expression given here for multicomponent fluids consists of two

terms: the first term is the heat transport by conduction which was given for pure

materials in Eq. 9.1-4, and the second term describes the heat transport by each

the diffusing species. The quantity is the partial molar enthalpy of species

There is actually one further contribution to the energy flux, related to a concen-

tration driving force-usually quite small-and this diffusion-thermo effect will be

discussed in Chapter 24. The thermal conductivity of

mixture-the

Eq.

19.3-3-is defined as the proportionality constant between the heat flux and the

temperature gradient in the absence of any mass fluxes.

We conclude this discussion with a few comments about the combined energy flux

By substituting

Eq.

19.3-3 into Eq.

(C)

of Table 19.2-2, we get after some minor rearranging:

In some situations, notably in films and low-velocity boundary layers, the contributions

ipv2v

and

are negligible. Then the dashed-underlined terms may be discarded.

This leads to

919.3 Summary of the Multicomponent Fluxes

591

Then use of Eqs.

(G)

and

(H)

of Table 17.8-1 leads finally to

Finally, for ideal gas mixtures, this expression can be further simplified by replacing the

partial molar enthalpies by the molar enthalpies

Equation

19.3-6

provides a stan-

dard starting point for solving one-dimensional problems in simultaneous heat and

mass transfer.'

The partial molar enthalpy E,, which appears in Eqs. 19.3-3 and 19.3-6, is defined for a multi-

component mixture as

The

Partial Molar

Enthalp

in which n, is the number of moles of species

in the mixture, and the subscript np indicates

that the derivative is to be taken holding the number or moles of each species other than

constant. The enthalpy H(n,, n,, n,,

. .

is an "extensive property," since, if the number of

moles of each component is multiplied by k, the enthalpy itself will be multiplied by

H(kn,, kn,, kn,,

kH(n,, n,, n,,

(19.3-8)

Mathematicians refer to this kind of function as being "homogeneous of degree 1." For such

functions Euler's theorem2 can be used to conclude that

(a)

Prove that, for a binary mixture, the partial molar enthalpies at a given mole fraction can

be determined by plotting the enthalpy per mole as a function of mole fraction, and then de-

termining the intercepts of the tangent drawn at the mole fraction in question (see Fig. 19.3-1).

This shows one way to get the partial molar enthalpy from data on the enthalpy of the

mixture.

(b)

How else could one get the partial molar enthalpy?

Fig.

19.3-1.

The "method of inter-

cepts" for determining partial molar

quantities in a binary mixture.

Sherwood,

Pigford, and

Wilke,

Mass Transfer,

McGraw-Hill, New York (1975),

Chapter 7.

Thomas Kilgore Sherwood

(1903-1976) was a professor at

MIT

for nearly 40 years, and then

taught at the University of California in Berkeley. Because of his many contributions to the field of mass

transfer, the Sherwood number (Sh) was named after him.

Greenberg,

Foundations

Applied

Mathematics,

Prentice-Hall, Englewood Cliffs,

N.J.

(1978),

p. 128;

Silbey and

Alberty,

Physical Chemistry,

3rd edition, Wiley, New York (2001), §§1.10,4.9,

and

6.10.

592

Chapter 19 Equations of Change for Multicomponent Systems

SOLUTION

(a)

Throughout this example, for brevity we omit the subscripts

indicating that these

quantities are held constant. First we write expressions for the intercepts as follows:

in which

H/(nA

n,)

H/n. To verify the correctness of Eq. 19.3-10, we rewrite the

ex-

pression in terms of

NOW

the expression

(dH/dnA),B implies that

is a function of nA and nB, whereas

(dH/dxA), implies that His a function of

and n. The relation between these kinds of deriva-

tives is given by the chain rule of partial differentiation. To apply this rule we need the rela-

tion between the independent variables, which, in this problem, are

Therefore we may write

Substitution of this into

Eq.

19.3-12 and use of Euler's theorem

nAEA

n,~,)

then gives

an identity. This proves the validity of Eq. 19.3-10, and the correctness of Eq. 19.3-11 can be

proved similarly.

(b)

One can also get

by using the definition in Eq. 19.3-7 and measuring the slope of the

curve of

versus n~, holding n, constant. One can also get

by measuring the enthalpy of

mixing and using

Often the enthalpy of mixing is neglected and the enthalpies of the pure substances are given

cPA(~

T")

and a similar expression for

i?,.

This is a standard assumption for gas

mixtures at low to moderate pressures.

Other methods for evaluating partial molar quantities may be found in current textbooks

on thermodynamics.

519.4

USE

THE EQUATIONS

CHANGE FOR MIXTURES

The equations of change in

519.2

can be used to solve all the problems of Chapter

18,

and

more difficult ones as well. Unless the problems are idealized or simplified, mixture

transport phenomena are quite complicated and usually numerical techniques are re-

quired. Here we solve a few introductory problems by way of illustration.

(a)

Develop expressions for the mole fraction profile x,(y) and the temperature profile

T(y)

for the system pictured in Fig. 19.4-1, given the mole fractions and temperatures at both film

Simulfaneous

Heat

and

boundaries

0 and

6).

Here a hot condensable vapor,

is diffusing at steady state

Mass Transporf'

through a stagnant film of noncondensable gas,

to a cold surface at

where

con-

denses. Assume ideal gas behavior and uniform pressure. Furthermore assume the physical

Colburn

and

Drew,

Trans.

Am.

Inst.

Chem.

Engrs.,

38,197-212 (1937).

919.4 Use of the Equations of Change for Mixtures

593

SOLUTION

Fig.

19.4-1.

Condensation of a hot vapor

on a cold surface in the presence of a non-

condensable gas

Cold

surface

properties to be constant, evaluated at some mean temperature and composition. Neglect ra-

diative heat transfer.

(b) Generalize the result for the situation where both

and

are condensing on the wall,

and allow for unequal film thicknesses for heat and mass transport.

(a)

To determine the desired quantities, we must solve the equations of continuity and en-

ergy for this system. Simplification of Eq. 19.1-10 and Eq. C of Table 19.2-1 for steady, one-

dimensional transport, in the absence of chemical reactions and external forces, gives

Continuity of

Energy:

Therefore, both

NAY

and e, are constant throughout the film.

To determine the mole fraction profile, we need the molar flux for diffusion of

through

stagnant

Insertion of Eq. 19.4-3 into Eq. 19.4-1 and integration gives the mole fraction profile (see 918.2)

Here we have taken

to be constant, at the value for the mean film temperature. We can

then evaluate the constant flux

NAY

from Eqs. 19.4-3 and 4:

Note that

NAY

is negative because species

is condensing. The last two expressions may be

combined to put the concentration profiles in an alternative form:

594

Chapter 19 Equations of Change for Multicomponent Systems

To get the temperature profile, we use the energy flux from Eq. 19.3-6 for an ideal gas along

with Eq. 9.8-8:

Here we have chosen To as the reference temperature for the enthalpy. Insertion of this

ex-

pression for e, into Eq. 19.4-2 and integration between the limits T

To at

0, and

gives

It can be seen that the temperature profile is not linear for this system except in the limit as

NA,&/k

0. Note the similarity between Eqs. 19.4-6 and 8.

The conduction energy flux at the wall is greater here than in the absence of mass trans-

fer. Thus, using a superscript zero to indicate the conditions in the absence of mass transfer,

we may write

We see then that the rate of heat transfer is directly affected by simultaneous mass transfer,

whereas the mass flux is not directly affected by simultaneous heat transfer. In applications at

temperatures below the normal boiling point of species

the quantity

~,,&/k

is small, and

the right side of Eq. 19.4-9 is very nearly unity (see Problem 19A.1). The interaction between

heat and mass transfer is further discussed in Chapter

22.

(b)

If both

and

are condensing at the wall, then Eqs. 19.4-1 and

when integrated, lead

to NAY

NAO and e,

e,, where the subscript

"0"

quantities are evaluated at

also in-

tegrate the analog of Eq. 19.4-1 for

to get N,,

NBo and obtain

In the second of these equations, we replace

by ?,*(T

To) and by

To), and

since the reference temperature is To, we may replace e, by

q,,

the conductive heat flux at

the

wall. In the first equation, we subtract xAO(NAO

NBO) from both sides to make the equation

similar in form to the temperature equation just obtained. Thus

Integration with respect to

and application of the boundary conditions at

0 gives

s19.4

Use of the Equations of Change for Mixtures

595

These are the concentration and temperature profiles in terms of the mass and heat fluxes.

Applications of the boundary conditions at the outer edges of the films-that is, at

and

ST,

respectively-give

These equations relate the fluxes to the film thicknesses and the transport properties. When

Eq.

19.4-14

is divided by Eq.

19.4-16

and Eq.

19.4-15

is divided by Eq.

19.4-17,

we get the con-

centration profiles in terms of the transport coefficients (analogously to Eqs.

19.4-6

and

8).

Equations

19.4-16

and

will be encountered again in

522.8.

A catalytic tubular reactor is shown in Fig.

19.4-2.

dilute solution of solute

in a solvent

is in fully developed, laminar flow in the region

When it encounters the catalytic wall

in the region

solute

is instantaneously and irreversibly rearranged to an isomer

Tddar Reactor

Write the diffusion equation appropriate for this problem, and find the solution for short

distances into the reactor. Assume that the flow is isothermal and neglect the presence of

SOLUTION

For the conditions stated above, the flowing liquid will always be very nearly pure solvent

The product

@BAS

can be considered constant, and the diffusion of

can be described by

the steady-state version of Eq.

19.1-14

(ignoring the presence of a small amount of the reaction

product

B).

The relevant equations of change for the system are then

Continuity

Motion:

We make the usual assumption that axial diffusion can be neglected with respect to axial con-

vection, and therefore delete the dashed-underlined term (compare with Eqs.

10.8-11

and

12).

Equation

19.4-19

can be solved to give the parabolic velocity profile v,(r)

v,,,,,[l

(r/M21.

When this result is substituted into Eq.

19.4-18,

we get

From

0 to

the

~il~t~ solution

inner surface of the tube is

coated

with

a catalyst

Fully-developed

irreversibly

laminar flow before and instantaneously

0 is reached on catalyst surface

Fig.

19.4-2.

Boundary conditions for a tubular reactor.

596

Chapter 19 Equations of Change for Multicomponent Systems

This is to be solved with the boundary conditions

B.C. 1:

B.C. 2:

B.C. 3:

c,,

finite

For short distances

into the reactor, the concentration

differs from

c,,

only near the wall,

where the velocity profile is practically linear. Hence we can introduce the variable

neglect curvature terms, and replace

B.C.

3 by a fictitious boundary condition at

(see

Example 12.2-2 for a detailed discussion of this method of treating the entrance region of the

tube).

The reformulated problem statement is then

with the boundary conditions

B.C. 1:

B.C. 2:

B.C. 3:

This problem can be solved by the method of combination of independent variables by seeking

a solution of the form

c,/cA0

f($,

where

(y/R)(2~~,,,,~~/9~~~z)"~.

One thus obtains the

ordinary differential equation

3r12f'

0, which can be integrated to give (see

Eq.

C.l-9)

This problem is mathematically analogous to the Graetz problem of Problem 12D.4,

that

problem being analogous to 1

(c,/c,,)

here.

Experiments of the type described here have proved useful for obtaining mass transfer

data at high Schmidt numbers.'

particularly attractive reaction is the reduction of ferri-

cyanide ions on metallic surfaces according to the reaction

in which ferricyanide and ferrocyanide take the place of

and

in the above development.

This electrochemical reaction is quite rapid under properly chosen conditions. Furthermore,

since it involves only electron transfer, the physical properties of the solution are almost en-

tirely unaffected. The forced diffusion effects neglected here may be suppressed by the addi-

tion of an indifferent electrolyte in ex~ess.~,~

Figure 19.4-3 shows schematically how oxygen and carbon monoxide combine at a catalytic

surface (palladium) to make carbon dioxide, according to the technologically important

Catalytic Oxidation

reaction5

of Carbon Monoxide

2C0

2C02

(1 9.4-30)

W. Hubbard and

Lightfoot,

Ind. Eng. Chem. Fundam.,

5,370-379 (1966).

Newman,

Electrochical Systems,

2nd edition, Prentice-Hall, Englewood Cliffs, N.J. (1991), §1.10.

Selman and

Tobias,

Advances in Chemical Engineering,

10,

Academic Press, New York,

N.Y. (1978),

pp.

212-318.

Gates,

Catalytic Chemistry,

Wiley, New York (1992),

pp.

356-362; C. N. Satterfield,

Heterogeneous Catalysis in Industrial Practice,

McGraw-Hill, New York, 2nd edition (1991), Chapter 8.