Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena

Подождите немного. Документ загружается.

918.4 Diffusion with a Homogeneous Chemical Reaction

557

Fig.

18.4-4.

Gas absorption

accompanied by an irreversible

first-order reaction.

Next we use assumption (d) above and equate the amount of

entering the main body

of liquid at

S over the total bubble surface

in the tank to the amount of

consumed in

the bulk of the liquid by chemical reaction:

Substitution of cA from Eq. 18.4-15 into Eq. 18.4-16 gives an expression for

cash

(V/SS)Q, sinh

When this result is substituted into Eq. 18.4-15, we obtain an expression for cA/cAO in terms of

and V/SS.

From this expression for the concentration profile we can then get the total rate of ab-

sorption with chemical reaction from NA,

-91AB(dcA/dz) evaluated at

0, thus:

N~zlz=o~

cosh

cA091AB

sinh

(

cosh

(V/SS)4 sinh

)

(18.4-18)

The result is plotted in Fig. 18.4-4.

It is seen here that the dimensionless absorption rate per unit area of interface,

I?,

in-

creases with

for all finite values of V/SS. At very low values of +-that is, for very slow re-

actions-I? approaches zero. For this limiting situation the liquid

nearly saturated with

dissolved gas, and the "driving force" for absorption is very small. At large values of

the di-

mensionless surface mass flux

increases rapidly with

and becomes very nearly indepen-

dent of V/SS. Under the latter circumstances, the reaction is so rapid that almost all of the

dissolving gas is consumed within the film. Then

is very nearly zero, and the bulk of the liq-

uid plays no significant role. In the limit as

becomes very large,

approaches

Somewhat more interesting behavior is observed for intermediate values of

It may be

noted that, for moderately large V/SS, there is a considerable range of

for which

is very

nearly unity. In this region the chemical reaction is fast enough to keep the bulk of the solu-

tion almost solute free, but slow enough to have little effect on solute transport in the film.

Such a situation will arise when the ratio

V/SS

of bulk to film volume is sufficient to offset the

higher volumetric reaction rate in the film. The absorption rate is then equal to the physical

absorption rate (that is, the rate for

k',"

0) for a solute-free tank. This behavior is frequently

observed in practice, and operation under such conditions has proven a useful means of char-

acterizing the mass transfer behavior of a variety of gas absorbers.'

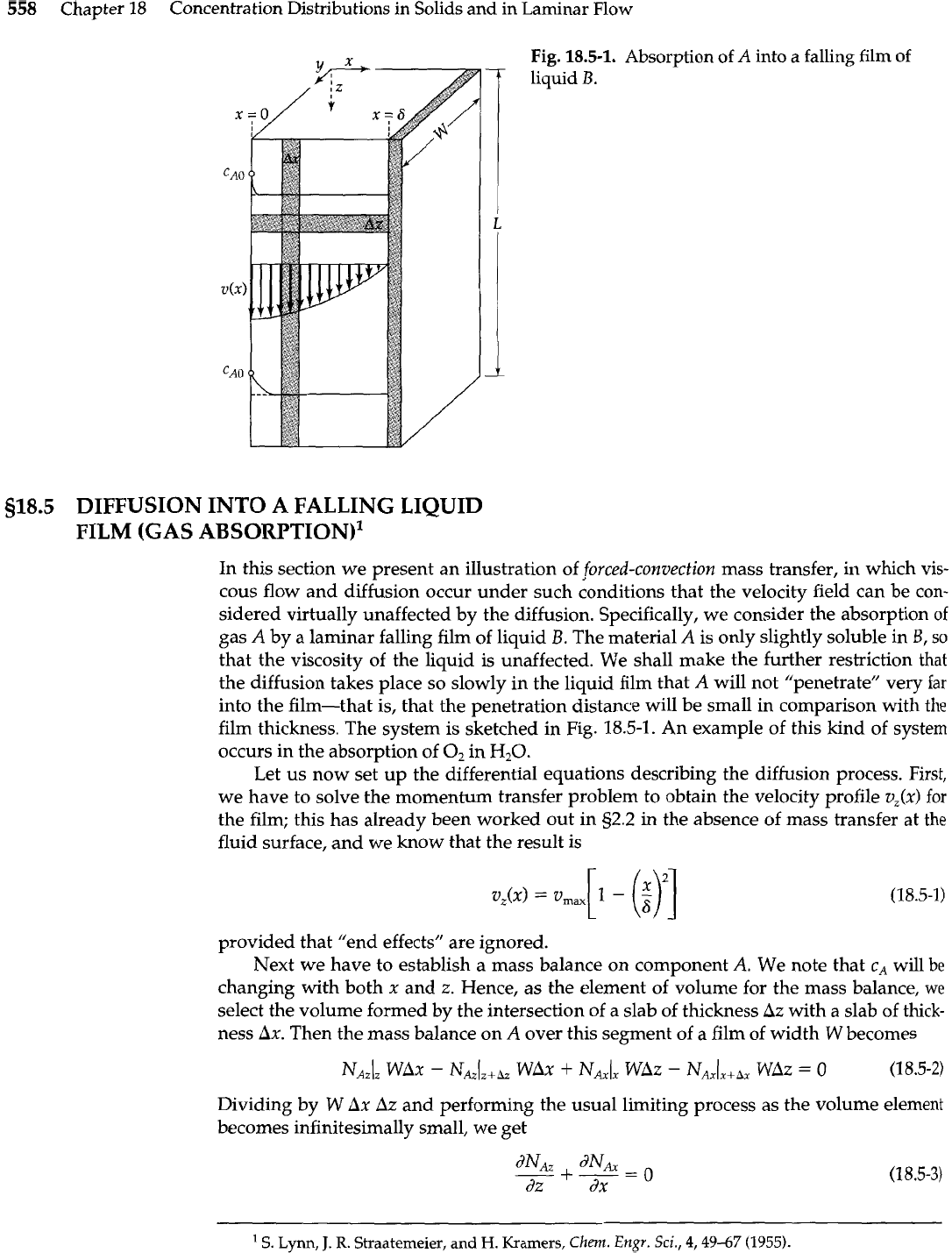
558

Chapter 18 Concentration Distributions in Solids and in Laminar Flow

Fig.

18.5-1.

Absorption of

into a falling

film

liquid

518.5

DIFFUSION INTO A FALLING LIQUID

FILM (GAS ABSORPTION)'

In this section we present an illustration of

forced-convection

mass transfer, in which vis-

cous flow and diffusion occur under such conditions that the velocity field can be con-

sidered virtually unaffected by the diffusion. Specifically, we consider the absorption of

gas

by a laminar falling film of liquid

The material

is only slightly soluble in

that the viscosity of the liquid is unaffected. We shall make the further restriction that

the diffusion takes place so slowly in the liquid film that

will not "penetrate" very far

into the film-that is, that the penetration distance will be small in comparison with

the

film thickness. The system is sketched in

Fig.

18.5-1. An example of this kind of system

occurs in the absorption of

H,O.

Let us now set up the differential equations describing the diffusion process.

First,

we have to solve the momentum transfer problem to obtain the velocity profile

vz(x)

for

the film; this has already been worked out in

52.2

in the absence of mass transfer at

the

fluid surface, and we know that the result is

provided that "end effects" are ignored.

Next we have to establish a mass balance on component

We note that

will

changing with both

and

Hence, as the element of volume for the mass balance,

select the volume formed

the intersection of a slab of thickness

with a slab of thick-

ness

Ax.

Then the mass balance on

over this segment of a film of width

becomes

Dividing by

and performing the usual limiting process as the volume element

becomes infinitesimally small, we get

Lynn,

Straatemeier,

and

Kramers,

Chem.

Engr.

Sci.,

4,4947

(1955).

s18.5

Diffusion Into a Falling Liquid Film (Gas Absorption)

559

Into this equation we now insert the expression for NA, and NA,, making appropriate

simplifications of Eq. 18.0-1. For the molar flux in the

direction, we write, assuming

constant

We discard the dashed-underlined term, since the transport of

in the

direction will

be primarily by convection. We have made use of Eq.

(M)

in Table 17.8-1 and the fact

that

is almost the same as

in dilute solutions. The molar flux in the

direction is

~CA

NAx

xA(NAx

NBx) -QAB

(18.5-5)

-----------..-----

Here we neglect the dashed-underlined term because in the x direction

moves pre-

dominantly by diffusion, there being almost no convective transport normal to the wall

on account of the very slight solubility of

Combining the last three equations, we

then get for constant

9,,

Finally, insertion of

Eq.

18.5-1 for the velocity distribution gives

as the differential equation for cA(x, z).

Equation 18.5-7 is to be solved with the following boundary conditions:

B.C.

atz=O, cA=O (18.5-8)

B.C.

c,, (18.5-9)

B.C.

~CA

atx=6,

-=O

(18.5-10)

The first boundary condition corresponds to the fact that the film consists of pure

at the

top

O),

and the second indicates that at the liquid-gas interface the concentration of

is determined

the solubility of

(that is, cAo). The third boundary condition states

that

cannot diffuse through the solid wall. This problem has been solved analytically in

the form of an infinite series? but we do not give that solution here. Instead, we seek only

a limiting expression valid for "short contact times," that is, for small values of

L/vm,,.

If, as indicated in Fig. 18.5-1, the substance

has penetrated only a short distance

into the film, then the species

"has the impression" that the film is moving throughout

with

velocity equal to

v,,,.

Furthermore if

does not penetrate very far, it does not

"sense" the presence of the solid wall at

6. Hence, if the film were of infinite thick-

ness moving with the velocity

v,,,,

the diffusing material "would not know the differ-

ence." This physical argument suggests (correctly) that we will get a very good result if

we replace

Eq.

18.5-7 and its boundary conditions by

B.C. 1:

B.C.

Pigford, PhD

thesis,

University

Illinois

(1941).

560

Chapter 18 Concentration Distributions in Solids and in Laminar Flow

An exactly analogous problem occurred in Example 4.1-1, which was solved by the

method of combination of variables. It is therefore possible to take over the solution to

that problem just by changing the notation. The solution is"

Then the total molar flow of

across the surface at

(i.e., being absorbed by a liquid

film of length

and width

erf

erfc

c~~

d49ABz/vrnax v4%ABz/vmax

The same result is obtained by integrating the product

vm,,cA

over the flow cross section

(see Problem 18C.3).

Equation 18.5-18 shows that the mass transfer rate is directly proportional to the

square root of the diffusivity and inversely proportional to the square root of the "expo-

sure time,"

texP

L/vrnax.

This approach for studying gas absorption was apparently first

proposed by Higbie.5

The problem discussed in this section illustrates the "penetration model" of mass

transfer. This model is discussed further in Chapters

and

22.

(18.5-16)

Estimate the rate at which gas bubbles of

are absorbed

liquid

as the gas bubbles rise

their terminal velocity

through a clean quiescent liquid.

Gas Absorption from

Rising Bubbles

In these expressions "erf

and "erfc

are the "error function" and the "complemen-

tary error function" of x, respectively. They are discussed in

gC.6

and tabulated in stan-

dard reference works4

Once the concentration profiles are known, the local mass flux at the gas-liquid in-

terface may be found as follows:

The solution is worked out in detail by the method of combination of variables in Example 4.1-1.

Abramowitz and I. A. Stegun,

Handbook ofMathematica1 Functions,

Dover, New York, 9th printing

(1973),

pp.

310 et seq.

Higbie,

Trans.

AIChE,

31,365-389 (1935). Ralph Wilmarth Higbie (190&1941), a graduate

the

University of Michigan, provided the basis for the "penetration model" of mass transfer. He worked at

I. du Pont de Nemours

Co., Inc., and also at Eagle-Picher Lead Co.; then he taught at the University

of Arkansas and the University of North Dakota.

518.5 Diffusion Into a Falling Liquid Film (Gas Absorption)

561

SOLUTION

Liquid

Fig.

18.5-2.

Absorption of gas

into liquid

Gas bubbles of moderate size, rising in liquids free of surface-active agents, undergo a

toroidal circulation (Rybczynski-Hadamard circulation) as shown in Fig. 18.5-2. The liquid

moves downward relative to each rising bubble, enriched in species

near the interface in

the manner of the falling film in Fig. 18.5-1. The depth of penetration of the dissolved gas into

the liquid is slight over the major part of the bubble, because of the motion of the liquid rela-

tive to the bubble and because of the smallness of the liquid-phase diffusivity

9AB.

Thus, as a

rough approximation, we can use Eq. 18.5-18 to estimate the rate of gas absorption, replacing

the exposure time

t,,,

L/v,,,

for the falling film by

D/v,

for the bubble, where

is the in-

stantaneous bubble diameter. This gives an estimate5 of the molar absorption rate, averaged

over the bubble surface, as

Here

cAO

is the solubility of gas

in liquid

at the interfacial temperature and partial pres-

sure of gas

Interestingly, the result in

Eq.

18.5-19 turns out to be correct for potential flow

of the liquid around the bubble (see Problem 4B.5). This equation has been approximately

confirmed6 for gas bubbles 0.3 to 0.5 cm in diameter rising through carefully purified water.

This system has also been analyzed for creeping flow7 and the result is (see Example

20.3-1)

instead of Eq. 18.5-19.

Trace amounts of surface-active agents cause a marked decrease in absorption rates from

small bubbles, by forming a "skin" around each bubble and thus effectively preventing inter-

nal circulation. The molar absorption rate in the small-diffusivity limit then becomes propor-

tional to the

power of the diffusivity, as for a solid sphere (see $3522.2 and

3).

A similar approach has been used successfully for predicting mass transfer rates during

drop formation at

capillary tip.8

Hammerton and

Garner,

Trans. Inst.

Chem.

Engrs.

(London),

32,

S18-524 (1954).

Levich,

Pkysicockemical Hydrodynamics,

Prentice-Hall, Englewood Cliffs,

N.J.

(1962),

408,

Eq.

72.9.

This reference gives many additional results, including liquid-liquid mass transfer and

surfactant effects.

Groothuis and

Kramers,

Chem.

Eng.

Sci., 4,17-25 (1955).

562

Chapter

Concentration Distributions in Solids and in Laminar Flow

Fig.

18.6-1.

Solid

dissolving into a falling film

of liquid

moving with a

fully

developed para-

Near wall Parabolic

bolic velocity profile.

velocity

profile of

fluid

Slightly soluble

wall made of

CA~

saturation

concentration

918.6

DIFFUSION INTO

FALLING LIQUID FILM

(SOLID DISSOLUTION)1

We now turn to a falling film problem that is different from the one discussed in the pre-

vious section. Liquid

is flowing in laminar motion down a vertical wall as shown in

Fig. 18.6-1. The film begins far enough up the wall so that

depends only on y for

For

the wall is made of a species

that is slightly soluble in

For short distances downstream, species

will not diffuse very far into the falling

film. That is,

will be present only in a very thin boundary layer near the solid surface.

Therefore the diffusing

molecules will experience a velocity distribution that is charac-

teristic of the falling film right next to the wall,

The velocity distribution is given

Eq.

2.2-18. In the present situation cos

1, and

and

At and adjacent to the wall (~/6)~

(y/6),

so that for this problem the velocity is, to a

very good approximation,

(pg6/p)y

ay.

This means that

Eq.

18.5-6, which is ap-

plicable here, becomes for short distances downstream

~CA

d2cA

ay-

9,,-

ay2

where

pg6/p. This equation is to be solved with the boundary conditions

B.C.

In the second boundary condition,

c,,

is the solubility of

The third boundary con-

dition is used instead of the correct one (dc,/dy

6),

since for short contact

times we feel intuitively that it will not make any difference. After all, since the mole-

Kramers and

Kreyger,

Chem.

Eng.

Sci., 6,4248

(1956); see also

Pigford,

Chem.

Eng.

Puog.

Symposium Series

No.

17,

Vol.

51,

pp.

79-92

(1955) for the analogous heat-conduction problem.

518.7 Diffusion and Chemical Reaction Inside a Porous Catalyst

563

cules of

penetrate only slightly into the film, they cannot get far enough to "see" the

outer boundary of the film, and hence they cannot distinguish between the true bound-

ary condition and the approximate boundary condition that we use. The same kind of

reasoning was encountered in Example 12.2-2 and Problem

12B.4.

The form of the boundary conditions in Eqs. 18.6-3 to 5 suggests the method of com-

bination of variables. Therefore we try

cA/cAO

f($, where

~(a/99~,z)'/~.

This com-

bination of the independent variables can be shown to be dimensionless, and the factor

"9"

is included to make the solution look neater.

When this change of variable is made, the partial differential equation in Eq. 18.6-2

reduces to an ordinary differential equation

with the boundary conditions

f(0)

1 and

f(w)

This second-order equation, which is of the form of Eq. C.1-9, has the solution

The constants of integration can then be evaluated using the boundary conditions, and

one obtains finally

for the concentration profiles, in which

~(2)

0.8930

is the gamma function of

the local mass flux at the wall can be obtained as follows

Then the molar flow of

across the entire mass transfer surface at

where

I?($)

r($)

1.1907.

. .

The problem discussed in 518.5 and the one discussed here are examples of two types

of asymptotic solutions that are discussed further in 920.2 and 520.3 and again in Chapter

22.

It is therefore important that these two problems be thoroughly understood. Note that

in s18.5,

(QAB~)1/2,

whereas in this section

(%AB~)2'3.

The differences in the ex-

ponents reflect the nature of the velocity gradient at the mass transfer interface: in 518.5,

the velocity gradient was zero, whereas in this section, the velocity gradient is nonzero.

518.7

DIFFUSION AND CHEMICAL REACTION

INSIDE A POROUS CATALYST

Up to this point we have discussed diffusion in gases and liquids in systems of simple

geometry. We now wish to apply the shell mass balance method and Fick's first law to

describe diffusion within

porous catalyst pellet. We make no attempt to describe the

564

Chapter

Concentration Distributions in Solids and in Laminar Flow

Concentration

concentrations

CAR

and

CAR

lyst

Fig.

18.7-1.

spherical catalyst that

is porous. For a magnified version

the inset, see Fig.

18.7-2.

Solid

Fig.

18.7-2.

Pores in the catalyst, in

which diffusion and chemical reac-

tion occur.

diffusion inside the tortuous void passages in the pellet. Instead, we describe the "aver-

aged diffusion of the reactant in terms of an "effective diff~sivity."',~,~

Specifically, we consider a spherical porous catalyst particle of radius R, as shown in

Fig. 18.7-1. This particle is in

catalytic reactor, where it is submerged in a gas stream

containing the reactant

and the product

In the neighborhood of the surface of the

particular catalyst particle under consideration, we presume that the concentration is

cA,

moles of

per unit volume. Species

diffuses through the tortuous passages in the cata-

lyst and is converted to

on the catalytic surfaces, as sketched in Fig. 18.7-2.

We start by making a mass balance for species

on a spherical shell of thickness

within a single catalyst particle:

Here

NAr(,

is the number of moles of

passing in the

direction through an imaginary

spherical surface at a distance

from the center of the sphere. The source term

4m2Ar

is the molar rate of production of

by chemical reaction in the shell of thickness

Ar.

Dividing by

437

and letting

gives

or, using the definition of the first derivative,

This limiting process is clearly in conflict with the fact that the porous medium is granu-

lar rather than continuous. Consequently, in

Eq.

18.7-3 the symbols

NAu

and RA cannot

interpreted as quantities having a meaningful value at a point. Rather we have to inter-

pret them as quantities averaged over a small neighborhood of the point in question-a

neighborhood small with respect to the dimension R, but large with respect to the

di-

mensions of the passages within the porous particle.

Thiele,

Ind.

Eng.

Chem.,

31,916-920 (1939).

Aris,

Chem.

Eng.

Sci.,

6,265-268 (1957).

A. Wheeler,

Advances

Catalysis,

Academic Press, New York

(1950),

Vol.

3, pp.

250-326.

518.7

Diffusion and Chemical Reaction Inside a Porous Catalyst

565

We now

define

an "effective diffusivity" for species

in the porous medium by

in which cA is the concentration of the gas

contained within the pores. The effective

diffusivity

must be measured experimentally. It depends generally on pressure and

temperature and also on the catalyst pore structure. The actual mechanism for diffusion

in pores is complex, since the pore dimensions may be smaller than the mean free path

of the diffusing molecules. We do not belabor the question of mechanism here but as-

sume only that

Eq.

18.7-4 can adequately represent the diffusion process (see 524.6).

When the preceding expression is inserted into

Eq.

18.7-3, we get, for constant

diffusivity

We now consider the situation where species

disappears according to a first-order

chemical reaction on the catalytic surfaces that form all or part of the "walls" of the

winding passages. Let a be the available catalytic surface per unit volume (of solids

voids). Then

-k','acA, and Eq. 18.7-5 becomes (see Eq. C.l-6)

This equation is to be solved with the boundary conditions that cA

cA, at r

and

that cA is finite at r

Equations containing the operator (1/r2)(d/dr)[r2(d/dr)l can frequently be solved by

using a "standard trick-namely, a change of variable cA/cA,

/r)f(r). The equation

for f(r) is then

This is a standard second-order differential equation, which can be solved in terms of ex-

ponential~ or hyperbolic functions. When it is solved and the result divided by

we get

the following solution of Eq. 18.7-6 in terms of hyperbolic functions (see 5C.5):

Application of the boundary conditions gives finally

In studies on chemical kinetics and catalysis one is frequently interested in the molar

flux

NAX

or the molar flow

WAR

at the surface r

When Eq. 18.7-9 is used in this expression, we get

This result gives the rate of conversion (in moles/sec) of

in a single catalyst particle

of radius

in terms of the parameters describing the diffusion and reaction processes.

566

Chapter

Concentration Distributions in Solids and in Laminar Flow

If the catalytically active surface were all exposed to the stream of concentration c,,,

then the species

would not have to diffuse through the pores to a reaction site. The

molar rate of conversion would then be given by the product of the available surface and

the surface reaction rate:

WAR,,

($d3)(a)(

-k;cAR> (18.7-12)

Taking the ratio of the last two equations, we get

TIA=-=-(4

W~R

coth

w~~,~

in which

-R

is the Thiele modulus,l encountered in s18.4. The quantity 7, is

called the efectiveness factor.'-4 It is the quantity by which

WAR,,

has to be multiplied to ac-

count for the intraparticle diffusional resistance to the overall conversion process.

For nonspherical catalyst particles, the foregoing results may be applied approxi-

mately by reinterpreting

We note that for a sphere of radius

the ratio of volume to

external surface is

R/3.

For nonspherical particles, we redefine

Eq.

18.7-13 as

where Vp and

are the volume and external surface of a single catalyst particle. The ab-

solute value of the conversion rate is then given approximately by

in which the quantity

-(V,/S,)

is a generalized mod~lus.~,~

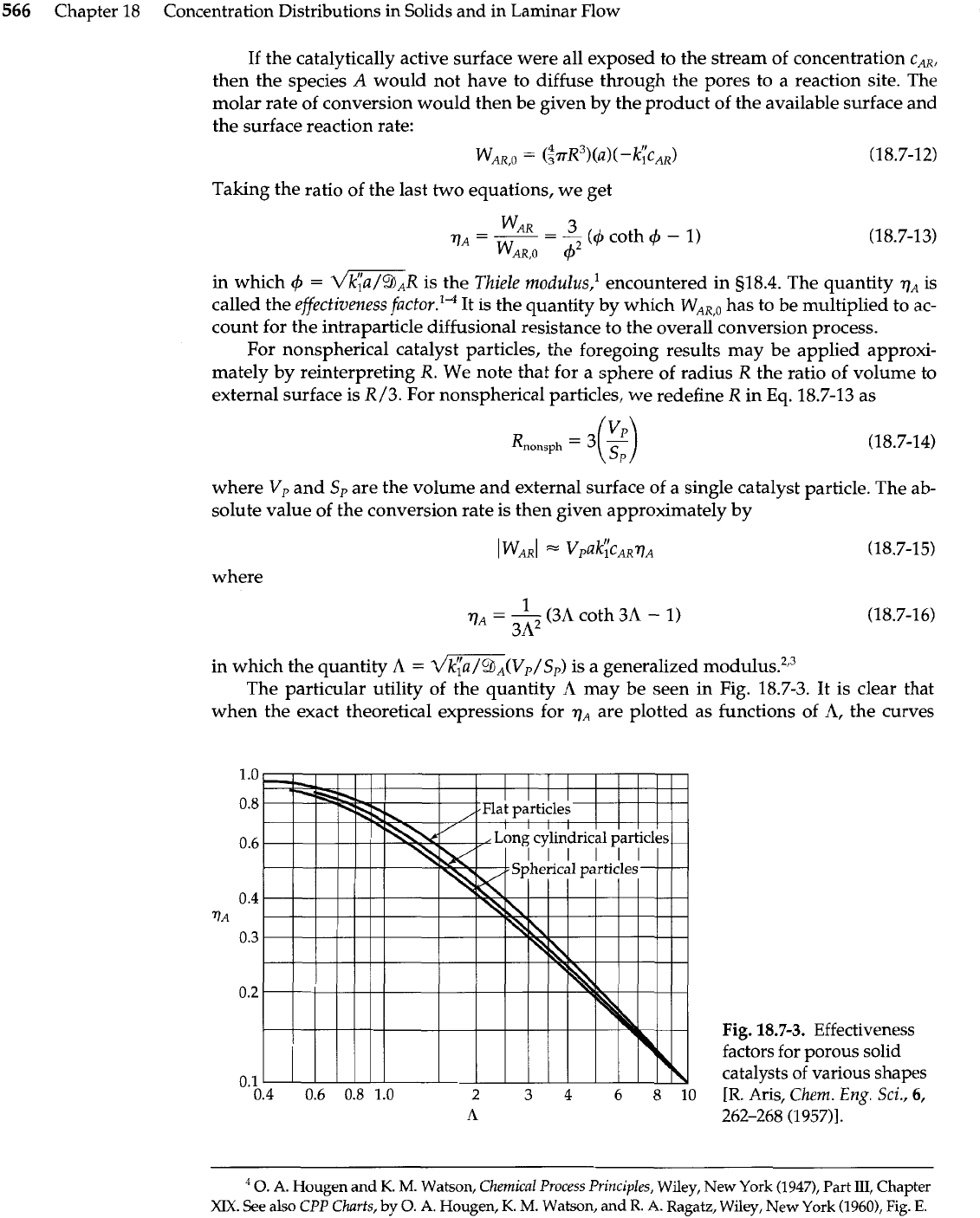
The particular utility of the quantity

may be seen in Fig. 18.7-3. It is clear that

when the exact theoretical expressions for

17,

are plotted as functions of

the curves

Fig.

18.7-3.

Effectiveness

factors for porous solid

catalysts of various shapes

[R.

Aris,

Chem.

Eng.

Sci.,

Hougen and

Watson,

Chemical

Process

Principles,

Wiley, New York

(1947),

Part

111,

Chapter

XU(.

See

also

CPP Charts,

Hougen,

Watson, and

Ragatz, Wiley, New York

(1960),

Fig.