Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena
Подождите немного. Документ загружается.


517.8
Summary of Mass and Molar Fluxes
537
Table
17.8-1
Notation for Mass and Molar Fluxes*
*Entries in the shaded boxes, involving the "hybrid fluxes"
j,$
and
J,,
are seldom needed; they
are
included only for the sake of
completeness.
Quantity
Velocity of species
a
(cm/s)
Table
17.8-2
Equivalent Forms of Fick's (First) Law of Binary Diffusion
With respect to
stationary axes
V,
(A)
Flux
Gradient
With respect to mass
average velocity
v
v,
-
v
(B)
Form of Fick's Law
With respect to molar
average velocity
v*
v,
-
v*
(C)

538
Chapter 17 Diffusivity and the Mechanisms of Mass Transport
517.9
THE MAXWELL-STEFAN EQUATIONS FOR
MULTICOMPONENT DIFFUSION IN GASES
AT LOW DENSITY
For multicomponent diffusion in gases at low density it has been shown1r2 that to a very good
approximation
XaXp
1
Vx,
=
-
C
-
(v,
-
vp)
=
-
2
-
(xpNa
-
x,Np)
a
=
1,2,3,. . .
,
N
(17.9-1)
p=1
Bop
p=1
c%p
The
9Iap
here are the binary diffusivities calculated from Eq. 17.3-11 or Eq. 17.3-12. There-
fore, for an N-component system,
~N(N
-
1) binary diffusivities are required.
Equations 17.9-1 are referred to as the Maxwell-Stefan equations, since Maxwell3
suggested them for binary mixtures on the basis of kinetic theory, and Stefanhener-
alized them to describe the diffusion in a gas mixture with
N
species. Later Curtiss
and Hirschfelder obtained Eqs. 17.9-1 from the multicomponent extension of the
Chapman-Enskog theory.
For dense gases, liquids, and polymers it has been shown that the Maxwell-Stefan
equations are still valid, but that the strongly concentration-dependent diffusivities ap-
pearing therein are not the binary diff~sivities.~
There is an important difference between binary diffusion and multicomponent dif-
f~sion.~ In binary diffusion the movement of species
A
is always proportional to the neg-
ative of the concentration gradient of species
A.
In multicomponent diffusion, however,
other interesting situations can arise: (i) reverse diffusion, in which a species moves
against its own concentration gradient; (ii) osmotic diffusion, in which a species diffuses
even though its concentration gradient is zero; (iii) dimsion barrier, when a species does
not diffuse even though its concentration gradient is nonzero. In addition, the flux of a
species is not necessarily collinear with the concentration gradient of that species.
QUESTIONS FOR DISCUSSION
How is the binary diffusivity defined? How is self-diffusion defined? Give typical orders
of
magnitude of diffusivities for gases, liquids, and solids.
Summarize the notation for the molecular, convective, and total fluxes for the three transport
processes. How does one calculate the flux of mass, momentum, and energy across a surface
with orientation
n?
Define the Prandtl, Schmidt, and Lewis numbers. What ranges of Pr and Sc can one expect to
encounter for gases and liquids?
How can you estimate the Lennard-Jones potential for
a
binary mixture, if you know the pa-
rameters for the two components of the mixture?
Of what value are the hydrodynamic theories of diffusion?
What is the Langevin equation? Why is it called a "stochastic differential equation"? What in-
formation can be obtained from it?
'
C.
F. Curtiss and
J.
0.
Hirschfelder,
J.
Chem. Phys.,
17,550-555 (1949).
For applications to engineering, see
E.
L.
Cussler,
Diffusion: Mass Transfer in
Fluid
Systems,
2nd
edition, Cambridge University Press
(1997);
R.
Taylor and
R.
Krishna,
Multicomyonent Mass Transfer,
Wiley,
New
York
(1993).
9.
C.
Maxwell,
Phil.
Mag.,
XIX, 19-32 (1860); XX, 21-32,33-36 (1868).
9.
Stefan,
Sitzungsber. his.
Akad.
Wiss. Wien,
LXIII(2), 63-124 (1871); LXV(2), 323-363 (1872).
C.
F.
Curtiss and
R.
6.
Bird,
Ind.
Eng.
Chern.
Res.,
38,2515-2522 (1999); 40,1791 (2001);
J.
Chem.
Phys.,
111,10362-10370 (1999).
H.
L.
Toor,
MChE Journal,
3,198-207 (1959).

Problems
539
7.
Compare and contrast the relation between binary diffusivity and viscosity for gases and for
liquids.
8.
How are the Maxwell-Stefan equations for multicomponent diffusion in gases related to the
Fick equations for binary systems?
9.
In a multicomponent mixture, does the vanishing of
N,
imply the vanishing of Vx,?
PROBLEMS
17A.1.
Prediction of a low-density binary diffusivity. Estimate BAB for the system methane-ethane
at 293K and 1 atm by the following methods:
(a) Equation 17.2-1.
(b) The corresponding-states chart in Fig. 17.2-1 along with
Eq.
17.2-3.
(c)
The Chapman-Enskog relation (Eq. 17.3-12) with Lennard-Jones parameters from
Appendix
E.
(dl The Chapman-Enskog relation (Eq. 17.3-12) with the Lennard-Jones parameters esti-
mated from critical properties.
Answers
(all in cm2/s): (a) 0.152; (b) 0.138; (c) 0.146; (d) 0.138.
17A.2.
Extrapolation of binary diffusivity to a very high temperature.
A
value of
9,,
=
0.151 cm2/s
has been reported1 for the system C0,-air at 293K and
1
atm. Extrapolate
9AR
to 1500K by the
following methods:
(a) Equation 17.2-1.
(b) Equation 17.3-10.
(c)
Equations 17.3-12 and 15, with Table E.2,
What do you conclude from comparing these results with the experimental value' of
2.45 cm2/s?
Answers
(all in cm2/s): (a) 2.96;
(b)
1.75; (c) 2.51
17A.3.
Self-diffusion in liquid mercury. The diffusivity of
H~~~~
in normal liquid Hg has been mea-
sured: along with viscosity and volume per unit mass. Compare the experimentally mea-
sured
with the values calculated with
Eq.
17.4-5.
17A.4.
Schmidt numbers for binary gas mixtures at low density. Use Eq. 17.3-11 and the data
given in Problem 1A.4 to compute Sc
=
p/pBAB for binary mixtures of hydrogen and Freon-
12 at x,
=
0.00,0.25,0.50,0.75, and 1.00, at 25°C and
1
atm.
Sample answers:
At
xA
=
0.00, Sc
=
3.43; at
x,
=
1.00,
Sc
=
0.407
17A.5.
Estimation of diffusivity for a binary mixture at high density. Predict
for an equimo-
lar mixture of
N,
and C2H6 at 288.2K and 40 atm.
(a) Use the value of
9,,
at 1 atrn from Table 17.1-1, along with Fig. 17.2-1.
(b) Use
Eq.
17.2-3 and Fig. 17.2-1.
Answers:
(a)
5.8
X
lop6
g-mole/cm
.
s;
(b) 5.3
X
g-mole/cm. s
'
Ts.
M.
Klibanova,
V. V.
Pomerantsev, and D.
A.
Frank-Kamenetskii,
I.
Tech. Phys.
(USSR),
12,14-30
(1942),
as quoted by
C.
R.
Wilke and
C.
Y.
Lee,
Ind.
Eng.
Chem.,
47,1253 (1955).
R.
E.
Hoffman,
1.
Chem. Phys.,
20,1567-1570 (1952).

540
Chapter 17 Diffusivity and the Mechanisms of Mass Transport
Diffusivity and Schmidt number for chlorine-air mixtures.
(a) Predict
$?JAB
for chlorine-air mixtures at 75°F and
1
atrn. Treat air as a single substance
with Lennard-Jones parameters as given in Appendix
E.
Use the Chapman-Enskog theory re-
sults in 517.3.
(b) Repeat (a) using Eq. 17.2-1.
(c)
Use the results of (a) and of Problem 1A.5 to estimate Schmidt numbers for chlorine-air
mixtures at
297K
and
1
atm for the following mole fractions of chlorine: 0,0.25,0.50,0.75, and
1.00.
Answers:
(a) 0.121 cm2/s; (b) 0.124 cm2/s; (c) Sc
=
1.27,0.832,0.602,0.463,0.372
The Schmidt number for self-diffusion.
(a) Use Eqs. 1.3-lb and 17.2-2 to predict the self-diffusion Schmidt number Sc
=
p/p$?JAA*
at
the critical point for a system with MA
=
MA*.
(b) Use the above result, along with Fig. 1.3-1 and Fig. 17.2-1, to predict Sc
=
p/p9IAA' at the
following states:
Phase Gas Gas Gas Liquid Gas Gas
Tr
0.7 1.0 5.0 0.7 1.0 2.0
Pr
0.0 0.0 0.0 saturation 1.0 1.0
Correction of high-density diffusivity for temperature. The measured value3 of for
a
mixture of 80 mole%
CH,
and 20 mole% C,H, at 313K and 136 atm is 6.0
X
g-mol/cm. s
(see Example 17.2-3). Predict c9AB for the same mixture at 136 atm and 351K, using Fig. 17.2-1.
Answer:
6.3
X
lop6
g-mole/cm. s
Ob~erved:~
6.33
X
g-mol/cm
-
s
Prediction of critical
c9,,
values. Figure 17.2-1 gives the low-pressure limit (c$?JAA,),
=
1.01
at
T,
=
1 and p,
+
0. At this limit, Eq. 17.2-13 gives
1.01(~9~,.),
=
2.2646
x
lo-'
JT,,
(L
+
l)
1
(17A.9-1)
MA MA*
dA+
a9,AA*
Here the argument
of
f19,
is reported%s
=
1.225 for Ar, Kr, and Xe. We use the
value 1 /O.77 from Eq. 1.4-11a as a representative average over many fluids.
(a) Combine Eq. 17A.9-1 with the relations
and Table E.2 to obtain Eq. 17.2-2 for
(dBAA*),
(b)
Show that the approximations
V,,==
CAB==
for Lennard-Jones parameters for the
A-B
interaction give
when the molecular parameters of each species are predicted according to Eqs. 1.4-lla,
c.
Combine these expressions with Eq. 17A.9-1 (with
AX
replaced by
B
and TcA by
m)
to
obtain Eq. 17.2-3 for (cQ,,),. The corresponding replacement of
p,
and T, in Fig. 17.2-1 by
and amounts to regarding the
A-B
collisions as dominant over collisions
of
like molecules in determining the value of
V.
J.
Berry
and
R.
C.
Koeller,
AIChE Journal,
6,274-280
(1960).
J. J.
van Loef and
E.
G.
D.
Cohen,
Physica
A,
156,522-533
(1989).

Problems
541
Estimation of liquid diffusivities.
(a)
Estimate the diffusivity for a dilute aqueous solution of acetic acid at 12.5"C, using the
Wilke-Chang equation. The density of pure acetic acid is 0.937 g/cm3 at its boiling point.
(b)
The diffusivity of a dilute aqueous solution of methanol at 15OC is about 1.28
X
10-' cm/s.
Estimate the diffusivity for the same solution at 100°C.
Answer:
(b)
6.7
X
cm/s
Interrelation of composition variables in mixtures.
(a)
Using the basic definitions in Eqs.
(A)
to
(G)
of Table 17.7-1, verify the algebraic relations
in Eqs.
(HI
to
(0).
(b)
Verify that, in Table 17.7-1, Eqs.
(P)
and
(Q)
simplify to Eqs. (P') and
(Q')
for binary
mixtures.
(c)
Derive Eqs. (P') and
(Q')
from Eqs.
(N)
and
(0).
Relations among fluxes in multicomponent systems.
Verify Eqs.
(K),
(O),
(T), and
(X)
of
Table 17.8-1 using only the definitions of concentrations, velocities, and fluxes.
Relations between fluxes in binary systems.
The following equation is useful for interrelat-
ing expressions in mass units and those in molar units in two-component systems:
Verify the correctness of this relation.
Equivalence of various forms of Fick's law for binary mixtures.
(a)
Starting with Eq.
(A)
of Table 17.8-2, derive
Eqs.
(B),
(D),
and (F).
(b)
Starting with Eq.
(A)
of Table 17.8-2, derive the folowing flux expressions:
What conclusions can be drawn from these two equations?
(c)
Show that Eq.
(F)
of Table 17.8-2 can be written as
Mass flux with respect to volume average velocity.
Let the
volume average velocity
in an
N-component mixture be defined by
in which
V,
is the partial molar volume of species
a.
Then define
j!
=
ph,
-
vm)
(17C.1-2)
as the mass flux with respect to the volume average velocity.
(a)
Show that for a binary system of
A
and
B,
To do this you will need to use the identity
cAVA
+
cBVB
=
1.
Where does this come from?
(b)
Show that Fick's first law then assumes the form
To verifv this vou will need the relation
V,vcA
+
V,VC,
=
0. What is the origin of this?

542
Chapter
17
Diffusivity and the Mechanisms of Mass Transport
17C.2.
Mass flux with respect to the solvent velocity.
(a)
In
a system with
N
chemical species, choose component
N
to be the solvent. Then define
to
be
the mass flux with respect to the solvent velocity. Verify that
jf
=
ja
-
(pa/~N)jN
(b)
For a binary system (labeling
B
as the solvent), show that
How does this result simplify for a very dilute solution of
A
in solvent
B?
17C.3.
Determination of Lennard-Jones potential parameters from diffusivity data of a
binary
gas
mixture.
(a) Use the following data5 for the system
H,O-0,
at
1
atm pressure to determine
(TAB
and
&AB/K:
9AB
(cm2/s)
0.47
0.69
0.94 1.22 1.52 1.85 2.20 2.58
One way to do this is as follows: (i) Plot the data as
~o~(T~'~/%~~)
versus log Ton a thin sheet
of graph paper. (ii) Mot versus KT/GAB on a separate sheet of graph paper to the same
scale. (iii) Superpose the first plot on the second, and from the scales of the two overlapping
plots, determine the numerical ratios (T/(KT/E,,)) and
((T~'~/%,,)/&,,,).
(iv) Use these two
ratios and
Eq.
17.3-11
to solve for the two parameters
(TAB
and
gAB/~.
'
R.
E.
Walker
and
A. A.
Westenberg,
J.
Chem.
Phys.,
32,436442
(1960);
R.
M.
Fristrom
and
A.
A.
Westenberg,
Flame Stuuctuue,
McGraw-Hill,
New
York
(19651,
p.
265.

Chapter
18
Concentration Distributions in
Solids and in Laminar
Flow
Shell mass balances; boundary conditions
Diffusion through
a
stagnant gas film
Diffusion with a heterogeneous chemical reaction
Diffusion with a homogeneous chemical reaction
Diffusion into
a
falling liquid film (gas absorption)
Diffusion into a falling liquid film (solid dissolution)
Diffusion and chemical reaction inside a porous catalyst
Diffusion in
a
three-component gas system
In Chapter
2
we saw how a number of steady-state viscous flow problems can be set up
and solved by making a
shell momentum balance.
In Chapter
9
we saw further how
steady-state heat-conduction problems can be handled by means of a
shell energy balance.
In this chapter we show how steady-state diffusion problems may be formulated by
shell
mass balances.
The procedure used here is virtually the same as that used previously:
a.
A
mass balance is made over a thin shell perpendicular to the direction of mass
transport, and this shell balance leads to a first-order differential equation, which
may be solved to get the mass flux distribution.
b.
Into this expression we insert the relation between mass flux and concentration
gradient, which results in a second-order differential equation for the concentra-
tion profile. The integration constants that appear in the resulting expression are
determined by the boundary conditions on the concentration and/or mass flux at
the bounding surfaces.
In Chapter 17 we pointed out that several kinds of mass fluxes are in common use.
For simplicity, we shall in this chapter use the combined flux NA-that is, the number of
moles of
A
that go through
a
unit area in unit time, the unit area being fixed in space. We
shall relate the molar flux to the concentration gradient by Eq.
(D)
of Table 17.8-2, which
for the z-component is
combined moIecuIar
convective
flux
flu
flux
Before
Eq.
18.0-1 is used, we usually have to eliminate NBZ. This can be done only if
something is known beforehand about the ratio Nh/NAZ. In each of the binary diffusion

544
Chapter 18 Concentration Distributions in Solids and in Laminar Flow
problems discussed in this chapter, we begin by specifying this ratio by physical or
chemical reasoning.
In this chapter we study diffusion in both nonreacting and reacting systems. When
chemical reactions occur, we distinguish between two reaction types: homogeneous, in
which the chemical change occurs in the entire volume of the fluid, and heterogeneous, in
which the chemical change takes place only in a restricted region, such as the surface of
a
catalyst. Not only is the physical picture different for homogeneous and heterogeneous
reactions, but there is also a difference in the way the two types of reactions are described
mathematically. The rate of production of a chemical species by homogeneous reaction ap-
pears as a source term in the differential equation obtained from the shell balance, just as
the thermal source term appears in the shell energy balance. The rate of production by
a
heterogeneous reaction, on the other hand, appears not in the differential equation, but
rather in the boundary condition at the surface on which the reaction occurs.
In order to set up problems involving chemical reactions, some information has to
be available about the rate at which the various chemical species appear or disappear
by
reaction. This brings us to the vast subject of chemical kinetics, that branch of physical
chemistry that deals with the mechanisms of chemical reactions and the rates at which
they occur.' In this chapter we assume that the reaction rates are described by means of
simple functions of the concentrations of the reacting species.
At this point we need to mention the notation to be used for the chemical rate con-
stants. For homogeneous reactions, the molar rate of production of species
A
may be
given by an expression of the form
Homogeneous reaction:
R
-
k"'
n
A
-
~CA
(18.0-2)
in which
RA
[=I
moles/cm3
.
s and cA
[=I
moles/cm3. The index n indicates the "order"
of the rea~tion;~ for a first-order reaction,
kp
[=I
l/s. For heterogeneous reactions, the
molar rate of production at the reaction surface may often be specified by a relation of
the form
Heterogeneous reaction:
NAZI
surface
=
k;c]12
Isuriace
(18.0-3)
in which NAZ
[=I
moles/cm2
.
s and c,
[=I
moles/cm3. Here
k','
[=I
cm/s. Note that the
triple prime on the rate constant indicates a volume source and the double prime a sur-
face source.
We begin in 518.1 with a statement of the shell balance and the kinds of boundary
conditions that may arise in solving diffusion problems. In 518.2 a discussion of diffu-
sion through a stagnant film is given, this topic being necessary to the understanding of
the film models of diffusional operations in chemical engineering. Then, in 5518.3 and
18.4 we given some elementary examples of diffusion with chemical reaction-both het-
erogeneous and homogeneous. These examples illustrate the role that diffusion plays in
chemical kinetics and the important fact that diffusion can significantly affect the rate of
a chemical reaction. In 5518.5 and
6
we turn our attention to forced-convection mass
transfer-that is, diffusion superimposed on a flow field. Although we have not in-
'
R.
J.
Silbey and
R.
A. Alberty,
Physical Chemistry,
3rd edition, Wiley, New York (2001), Chapter 18.
Not all rate expressions are of the simple form of
Eq.
18.0-2. The reaction rate may depend in a
complicated way on the concentration of all species present. Similar remarks hold for
Eq.
18.0-3. For
detailed information on reaction rates see
Table of Chemical Kinetics, Homogeneous Reactions,
National
Bureau of Standards, Circular 510 (1951), Supplement No. 1 to Circular 510 (1956). This reference is
now being supplemented by a data base maintained by
NIST
at
"http://kinetics.nist.gov/."
For
heterogeneous reactions,
see
R.
Mezaki and
H.
Inoue,
Rate Equations of Solid-Catalyzed Renctions,
U.
of
Tokyo Press, Tokyo (1991). See also
C.
G.
Hill,
Chemical Engineering Kinetics and Reactor Design: An
Introduction,
Wiley, New York (1977).

518.2 Diffusion Through a Stagnant Gas
Film
545
cluded an example of free-convection mass transfer, it would have been possible to par-
allel the discussion of free-convection heat transfer given in 510.9. Next, in 518.7 we dis-
cuss diffusion in porous catalysts. Finally, in the last section we extend the evaporation
problem of 518.2 to a three-component system.
818.1
SHELL MASS BALANCES; BOUNDARY CONDITIONS
The diffusion problems in this chapter are solved by making mass balances for one or
more chemical species over a thin shell of solid or fluid. Having selected an appropriate
system, the law of conservation of mass of species
A
in a binary system is written over
the volume of the shell in the form
rate of rate of rate of production of
(18.1-1)
homogeneous reaction
The conservation statement may, of course, be expressed in terms of moles. The chemical
species
A
may enter or leave the system by diffusion (i.e., by molecular motion) and also
by virtue of the overall motion of the fluid (i.e., by convection), both of these being in-
cluded in
NA.
In addition, species
A
may be produced or consumed by homogeneous
chemical reactions.
After a balance is made on a shell of finite thickness by means of Eq. 18.1-1, we then
let the thickness become infinitesimally small. As a result of this process
a
differential
equation for the mass (or molar) flux is generated. If, into this equation, we substitute the
expression for the mass (or molar) flux in terms of the concentration gradient, we get a
differential equation for the concentration.
When this differential equation has been integrated, constants of integration appear,
and these have to be determined by the use of boundary conditions. The boundary con-
ditions are very similar to those used in heat conduction (see §10.1):
a.
The concentration at a surface can be specified; for example,
xA
=
x,,.
b.
The mass flux at a surface can be specified; for example,
NAz
=
N,,.
If the ratio
NB,/NAz
is known, this is equivalent to giving the concentration gradient.
c.
If diffusion is occurring in a solid, it may happen that at the solid surface sub-
stance
A
is lost to a surrounding stream according to the relation
in which
NAO
is the molar flux at the surface,
CAO
is the surface concentration,
cAb
is
the concentration in the bulk fluid stream, and the proportionality constant
kc
is a
"mass transfer coefficient." Methods of correlating mass transfer coefficients are
discussed in Chapter
22.
Equation 18.1-2 is analogous to "Newton's law of cool-
ing" given in Eq. 10.1-2.
d.
The rate of chemical reaction at the surface can be specified. For example, if sub-
stance
A
disappears at a surface by a first-order chemical reaction, then
NA@
=
k;cA0.
That is, the rate of disappearance at a surface is proportional to the surface
concentration, the proportionality constant
k;
being a first-order chemical rate
coefficient.
$18.2
DIFFUSION THROUGH A STAGNANT GAS FILM
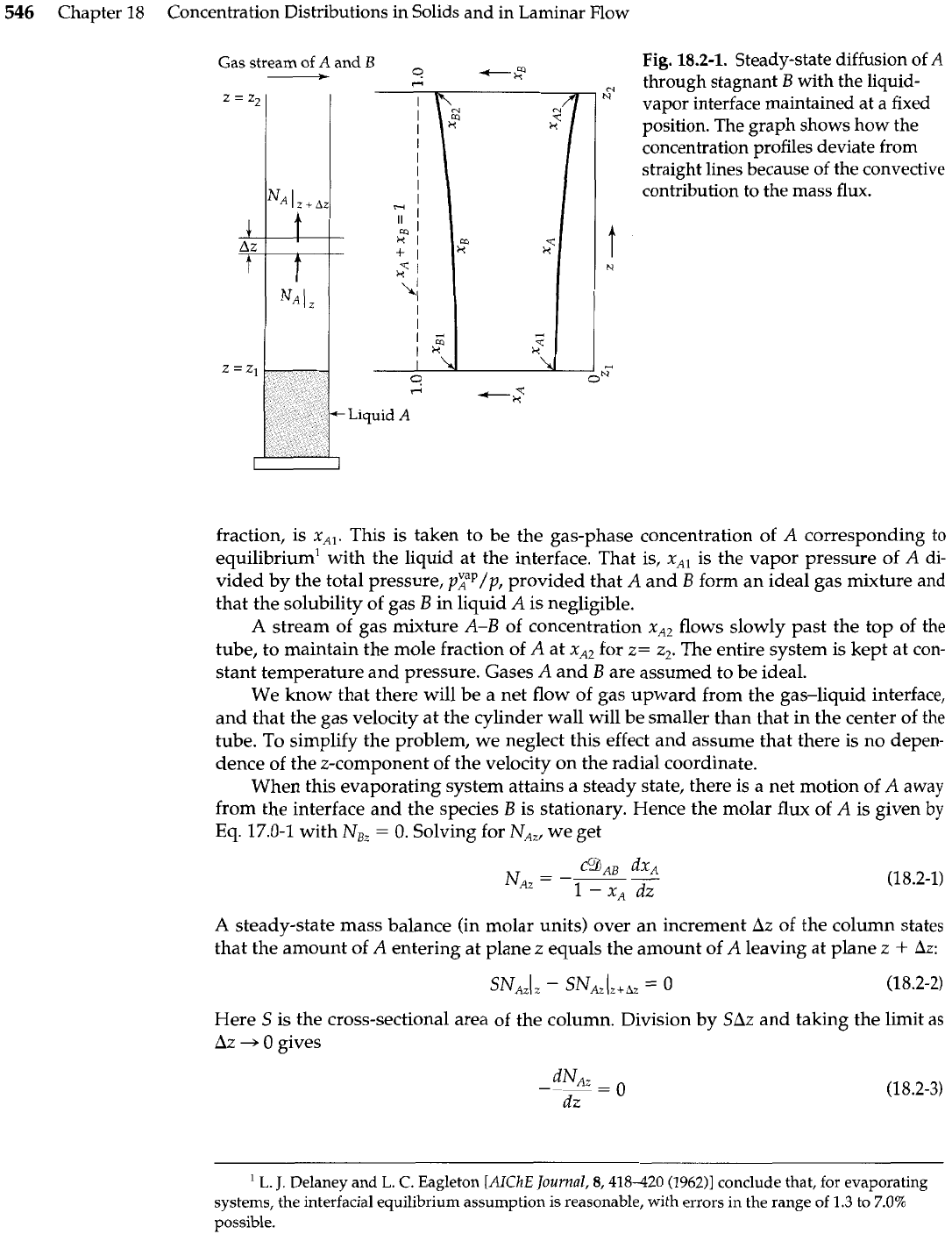
Let us now analyze the diffusion system shown in Fig. 18.2-1 in which liquid
A
is evapo-
rating into gas
B.
We imagine there is some device that maintains the liquid level at
z
=
2,.
Right at the liquid-gas interface, the gas-phase concentration of
A,
expressed as mole
546
Chapter
18
Concentration Distributions in Solids and in Laminar Flow
Gas stream of
A
and
B
9
F
I
I
I
I
;;
I
m
I
H
I
+
I
2'
1;
I
I
I
-
I
I
9
*
Liquid
A
Fig.
18.2-1.
Steady-state diffusion of
A
through stagnant
B
with the liquid-
vapor interface maintained at a fixed
position. The graph shows how the
concentration profiles deviate from
straight lines because
of
the convective
contribution to the mass flux.
fraction, is xAl. This is taken to be the gas-phase concentration of
A
corresponding to
equilibrium1 with the liquid at the interface. That is, xAl is the vapor pressure of
A
di-
vided by the total pressure,
pFp/p,
provided that
A
and
B
form an ideal gas mixture and
that the solubility of gas
B
in liquid
A
is negligible.
A
stream of gas mixture
A-B
of concentration
XA2
flows slowly past the top of the
tube, to maintain the mole fraction of
A
at x,, for
z=
z2.
The entire system is kept at con-
stant temperature and pressure. Gases
A
and
B
are assumed to be ideal.
We know that there will be a net flow of gas upward from the gas-liquid interface,
and that the gas velocity at the cylinder wall will be smaller than that
in
the center of the
tube. To simplify the problem, we neglect this effect and assume that there is no depen-
dence of the z-component of the velocity on the radial coordinate.
When this evaporating system attains a steady state, there is a net motion of
A
away
from the interface and the species
B
is stationary. Hence the molar flux of
A
is given
by
Eq.
17.0-1
with NBz
=
0.
Solving for NAz, we get
A
steady-state mass balance (in molar units) over an increment
Az
of the column states
that the amount of
A
entering at plane
z
equals the amount of
A
leaving at plane
z
+
Az:
Here
S
is the cross-sectional area of the column. Division by
SAz
and taking the limit
as
Az
+
0
gives
L.
J.
Delaney and
L.
C.
Eagleton
[AICkE
Journal,
8,418420 (196211
conclude that, for evaporating
systems, the interfacial equilibrium assumption is reasonable, with errors in the range of
1.3
to
7.0%
possible.
