Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena
Подождите немного. Документ загружается.

6j17.1 Fick's Law of Binary Diffusion (Molecular Mass Transport)
517
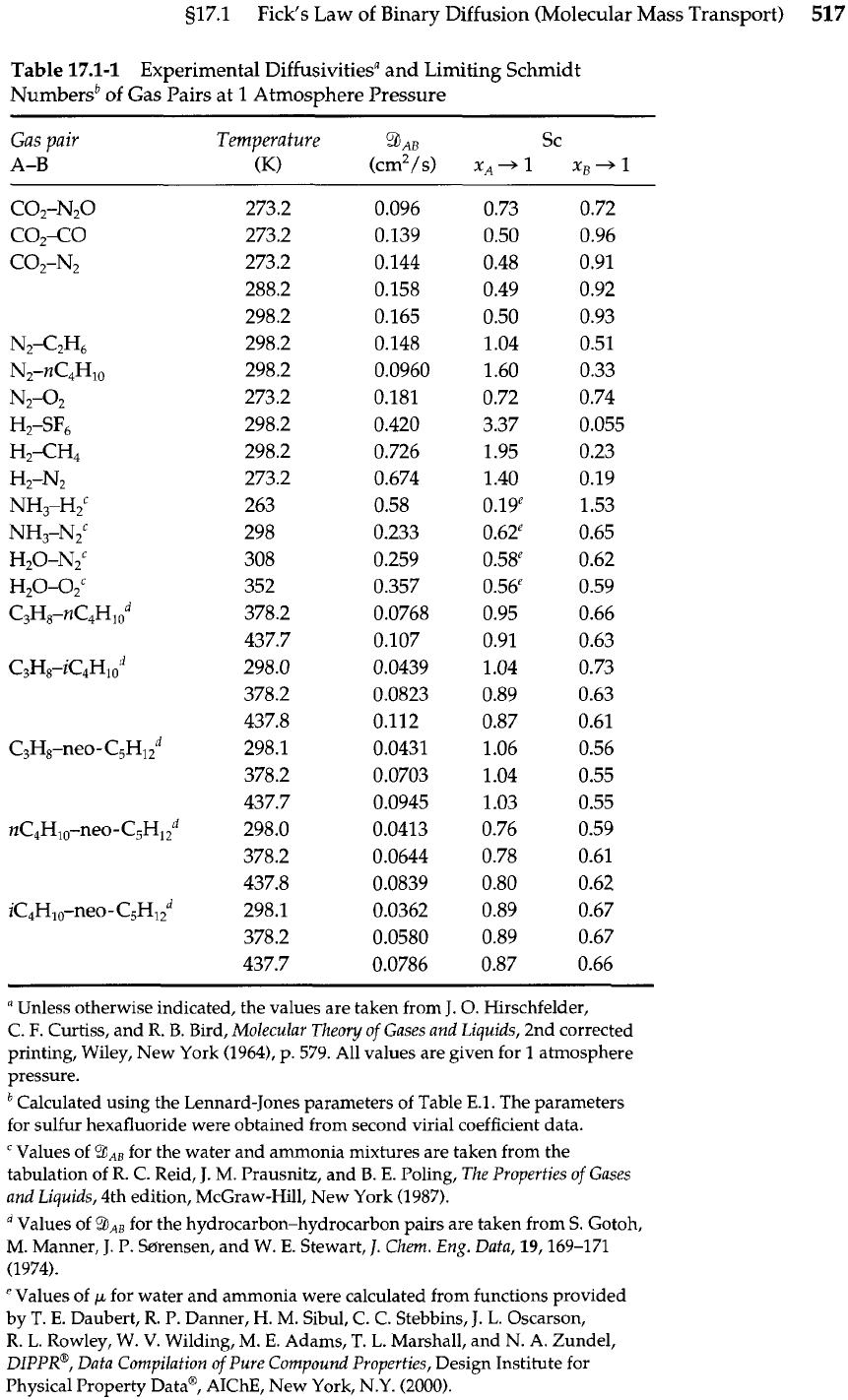
Table
17.1-1
Experimental Diffusivitiesa and Limiting Schmidt
Numbersb of Gas Pairs at 1 Atmosphere Pressure
Gas pair
Temperature
9
AB
Sc
A-B
(K)
(cm2/s) x~+1 xB+l
a
Unless otherwise indicated, the values are taken from
J.
0.
Hirschfelder,
C.
F.
Curtiss, and
R.
B.
Bird,
Molecular Theoy of Gases and Liquids,
2nd corrected
printing, Wiley, New York (1964), p. 579. All values are given for
1
atmosphere
pressure.
Calculated using the Lennard-Jones parameters of Table
E.1.
The parameters
for sulfur hexafluoride were obtained from second virial coefficient data.
'
Values of
aAB
for the water and ammonia mixtures are taken from the
tabulation of
R.
C.
Reid, J. M. Prausnitz, and
B.
E.
Poling,
The Properties of Gases
and Liquids,
4th edition, McGraw-Hill, New York (1987).
Values of
%,,
for the hydrocarbon-hydrocarbon pairs are taken from S. Gotoh,
M.
Manner,
J.
P.
Sdrensen, and
W.
E.
Stewart,
J.
Chem. Eng. Data,
19,169-171
(1974).
"Values of
p
for water and ammonia were calculated from functions provided
by
T.
E.
Daubert,
R.
P.
Danner,
H.
M. Sibul, C. C. Stebbins,
J.
L. Oscarson,
R.
L.
Rowley, W. V. Wilding, M.
E.
Adams,
T.
L.
Marshall, and
N.
A.
Zundel,
DIPPR@, Data Compilation of Pure Compound Properties,
Design Institute for
Physical Property Datao, AIChE,
New
York, N.Y.
(2000).

518
Chapter
17
Diffusivity and the Mechanisms of Mass Transport
Table
17.1-2
Experimental Diffusivities in the
Liquid
state"'
Water
Ethanol
Water
Chlorobenzene Bromobenzene
10.10 0.0332
0.2642
0.5122
0.7617
0.9652
39.92 0.0332
0.2642
0.5122
0.7617
0.9652
0.131
0.222
0.358
0.454
0.524
0.026
0.266
0.408
0.680
0.880
0.944
a
The data for the first two pairs are taken from a review article by
P.
A.
Johnson and
A.
L.
Babb,
Chem.
Reus.,
56,387453 (1956). Other summaries of experimental results may
be
found in:
P.
W.
M.
Rutten,
Diffusion in Liquids,
Delft University Press, Delft, The Netherlands (1992);
L.
J.
Gosting,
Adv. in Protein
Chem.,
Vol.
XI,
Academic Press, New York (1956);
A.
Vignes,
I.
E.
C. Funliamentals,
5,189-199 (1966).
The ethanol-water data were taken from
M. T.
Tyn and
W. F.
Calus,
J.
Chem. Eng. Data,
20,310-316
(1975).
Table
17.1-3
Experimental Diffusivities in the Solid Statea
Si02
Pyrex
"
It is presumed that in each of the above pairs, component
A
is
present
only in very small amounts. The data are taken from
R.
M. Barrer,
Diffusion
in and through Solids,
Macmillan, New York (1941), pp. 141,222, and 275.
s17.1 Fick's Law of Binary Diffusion (Molecular Mass Transport)
519
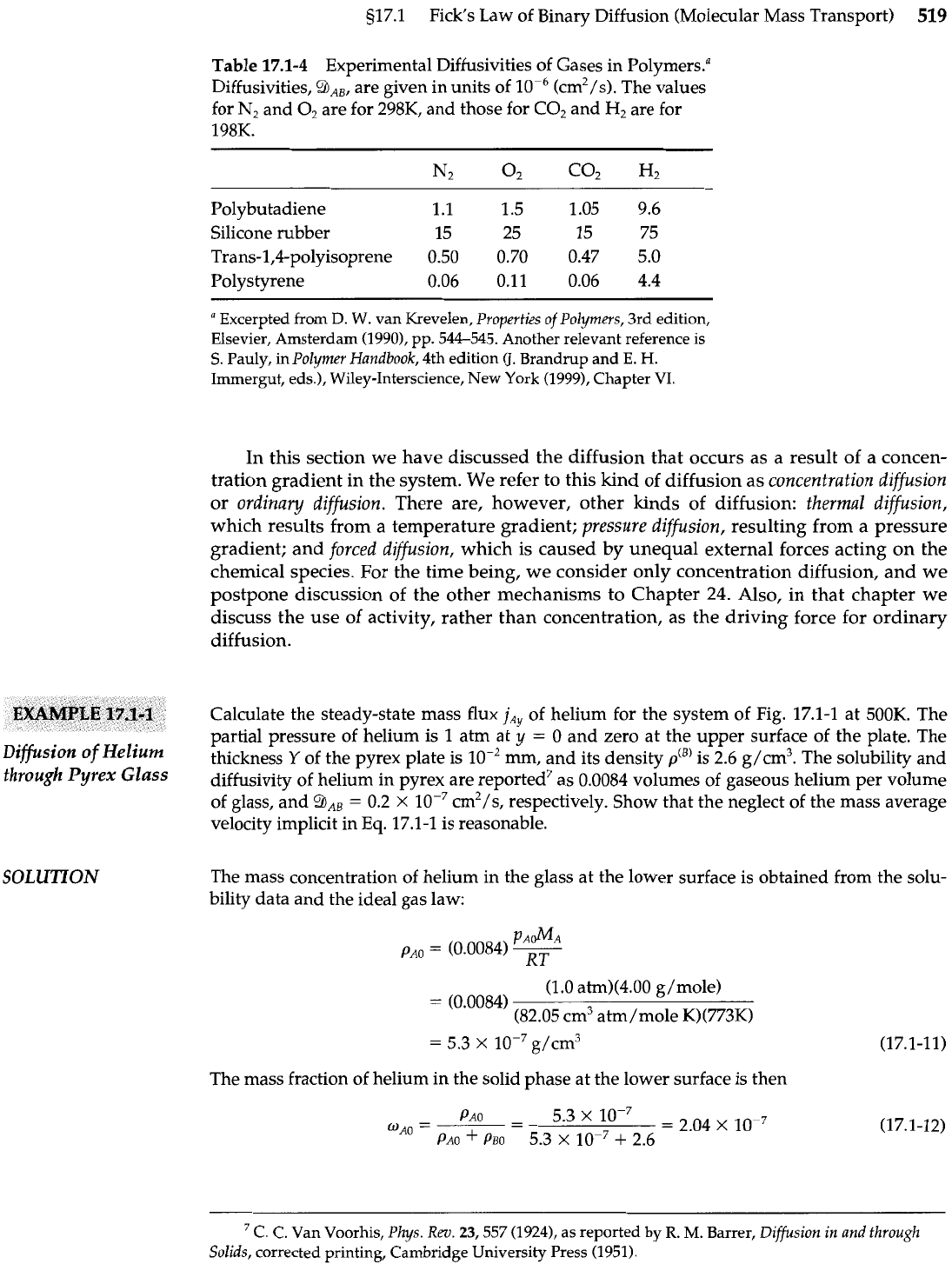
Table
17.1-4
Experimental Diffusivities of Gases in Polymers."
Diffusivities, 9AB, are given in units of
lop6
(cm2/s). The values
for N2 and O2 are for 298K, and those for C02 and
H2
are for
198K.
Polybutadiene 1.1
1.5 1.05 9.6
Silicone rubber 15
25 15 75
Trans-l,4-polyisoprene
0.50
0.70 0.47 5.0
Polystyrene
0.06 0.11
0.06 4.4
"
Excerpted horn
D.
W.
van Krevelen,
Properties of Polymers,
3rd edition,
Elsevier, Amsterdam (1990), pp. 544-545. Another relevant reference is
S.
Pauly, in
Polymer Handbook,
4th edition
(J.
Brandrup and E.
H.
Immergut, eds.), Wiley-Interscience, New York (1999), Chapter VI.
In this section we have discussed the diffusion that occurs as a result of a concen-
tration gradient in the system. We refer to this kind of diffusion as concentration diffusion
or ordinay diffusion. There are, however, other kinds of diffusion: thermal diflusion,
which results from a temperature gradient; pressure diffusion, resulting from a pressure
gradient; and forced diffusion, which is caused by unequal external forces acting on the
chemical species. For the time being, we consider only concentration diffusion, and we
postpone discussion of the other mechanisms to Chapter
24.
Also, in that chapter we
discuss the use of activity, rather than concentration, as the driving force for ordinary
diffusion.
Calculate the steady-state mass flux jAy of helium for the system of Fig. 17.1-1 at 500K. The
partial pressure of helium is
1
atm at
y
=
0 and zero at the upper surface of the plate. The
Difision
of
thickness
Y
of the pyrex plate is
mm, and its density
p'B'
is 2.6 g/cm3. The solubility and
through
Pyrex
Glass
diffusivity of helium in pyrex are reported7 as 0.0084 volumes of gaseous helium per volume
of glass, and
9,,
=
0.2
X
cm2/s, respectively. Show that the neglect of the mass average
velocity implicit in Eq. 17.1-1 is reasonable.
SOLUTION
The mass concentration of helium in the glass at the lower surface is obtained from the solu-
bility data and the ideal gas law:
The mass fraction of helium in the solid phase at the lower surface is then
C. C. Van Voorhis,
Phys.
Rev.
23,557
(1924),
as
reported by
R.
M.
Barrer,
Diffusion in and through
Solids,
corrected printing, Cambridge University Press (1951).

520
Chapter 17 Diffusivity and the Mechanisms of Mass Transport
We may now calculate the flux of helium from Eq. 17.1-1 as
Next, the velocity of the helium can be obtained from Eq. 17.1-4:
At the lower surface of the plate
(y
=
0) this velocity has the value
-
1.05
X
10-I' g/cm2
s
v~yly=u
-
+
v,,
=
1.98
X
lop5
cm/s
+
vYo
(17.1-15)
5.3
x
lop7
g/cm3
The corresponding value
v,,
of the mass average velocity of the glass-helium system at
y
=
0
is then obtained from Eq. 17.1-3
Thus it is safe to neglect
vy
in
Eq.
17.1-14, and the analysis of the experiment in Fig. 17.1-1
at
steady state is accurate.
Show that only one diffusivity is needed to describe the diffusional behavior of a binary
mixture.
The Equivalence
of
9,,
and
9,
SOLUTION
We begin by writing Eq. 17.1-6 as follows:
The second form of this equation follows from the fact that
w~
+
w,
=
1.
We next use the vec-
tor equivalents of Eqs. 17.1-3 and 4 to write
Interchanging
A
and
B
in this expression shows that
jA
=
-jB.
Combining this with the sec-
ond form of Eq. 17.1-17 then gives
Comparing this with Eq. 17.1-5 gives
9BA
=
BAR.
We find that the order of subscripts is unim-
portant for a binary system and that only one diffusivity is required to describe the diffu-
sional behavior.
However, it may well be that the diffusivity for a dilute solution of
A
in
B
and that for
a
dilute solution of
B
in
A
are
numerically
different. The reason for this is that the diffusivity
is
concentration-dependent, so that the two limiting values mentioned above are the values of
the diffusivity
BRA
=
91AB
at two different concentrations.

517.2
Temperature and Pressure Dependence of Diffusivities
521
517.2
TEMPERATURE AND PRESSURE
DEPENDENCE OF DIFFUSIVITIES
In this section we discuss the prediction of the diffusivity
9,,
for binary systems by cor-
responding-states methods. These methods are also useful for extrapolating existing
data. Comparisons of many alternative methods are available in the literature.'f2
For binary gas mixtures at low pressure,
%,,
is inversely proportional to the pressure,
increases with increasing temperature, and is almost independent of the composition for a
given gas pair. The following equation for estimating
'3,,
at low pressures has been devel-
oped3 from a combination of kinetic theory and corresponding-states arguments:
Here
%,,
[=I
cm2/s,
p
[=I
atm, and T
[=I
K.
Analysis of experimental data gives the di-
mensionless constants
a
=
2.745
x
lop4
and
b
=
1.823 for nonpolar gas pairs, excluding
helium and hydrogen, and
a
=
3.640
x
lop4
and
b
=
2.334 for pairs consisting of H,O
and a nonpolar gas. Equation 17.2-1 fits the experimental data at atmospheric pressure
within an average deviation of
6
to 8%. If the gases
A
and
B
are nonpolar and their
Lennard-Jones parameters are known, the kinetic-theory method described in the next
section usually gives somewhat better accuracy.
At high pressures, and in the liquid state, the behavior of
%,,
is more complicated.
The simplest and best understood situation is that of self-diffusion (interdiffusion of la-
beled molecules of the same chemical species). We discuss this case first and then extend
the results approximately to binary mixtures.
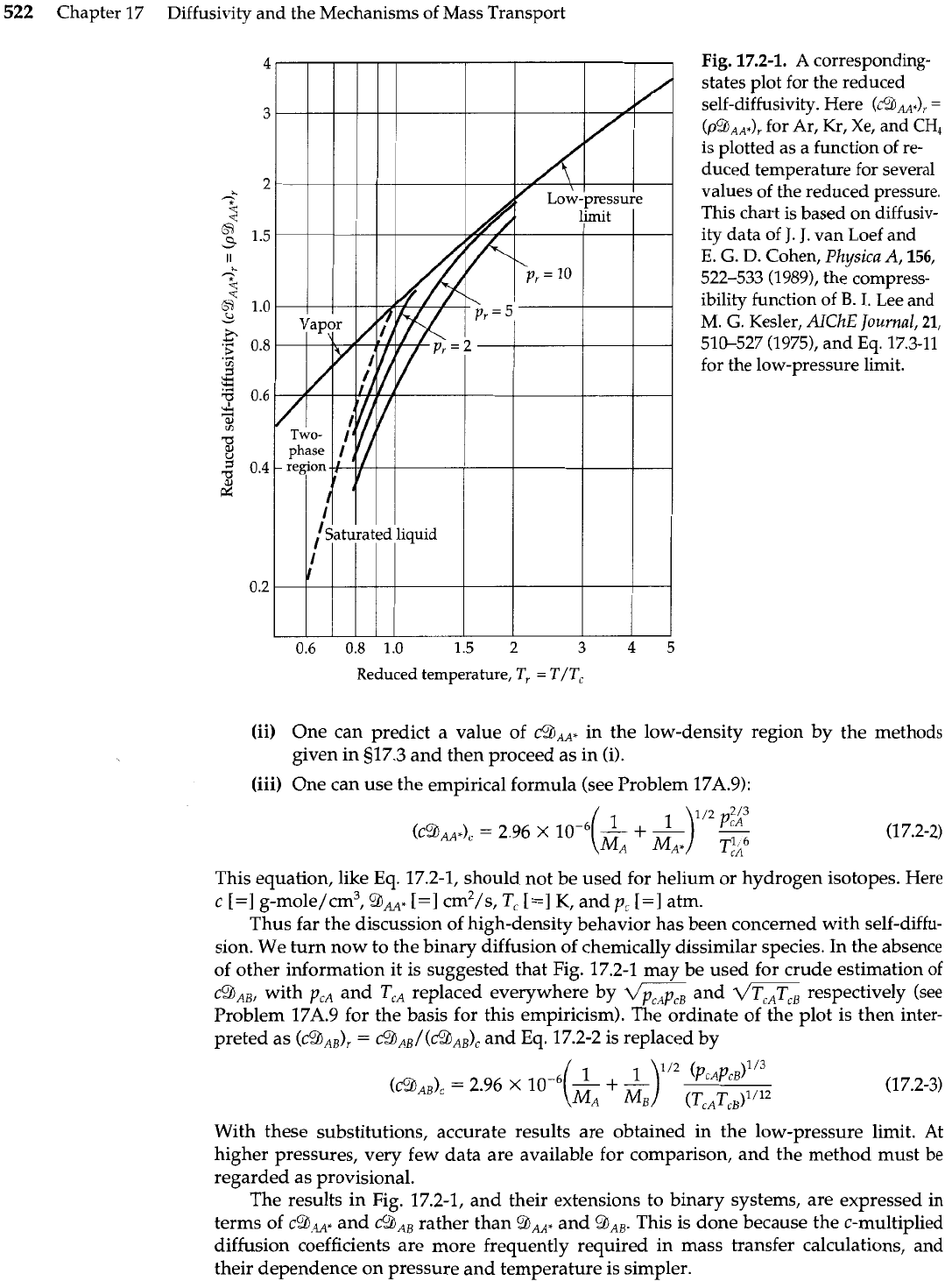
A corresponding-states plot of the self-diffusivity
%AA*
for nonpolar substances is
given in Fig. 17.2-1.4 This plot is based on self-diffusion measurements, supplemented by
molecular dynamics simulations and by kinetic theory for the low-pressure limit. The or-
dinate is c5JAA* at pressure
p
and temperature
T,
divided by
cgAA+
at the critical point.
This quantity is plotted as a function of the reduced pressure
p,
=
p/p,
and the reduced
temperature
T,
=
T/T,. Because of the similarity of species
A
and the labeled species
A",
the critical properties are all taken as those of species
A.
From Fig. 17.2-1 we see that
c9,*
increases strongly with temperature, especially
for liquids. At each temperature
c9,,$
decreases toward zero with increasing pressure.
With decreasing pressure,
~9~"
increases toward a low-pressure limit, as predicted by
kinetic theory (see 517.3). The reader is warned that this chart is tentative, and that the
lines, except for the low-density limit, are based on data for a very few substances: Ar,
Kr, Xe, and CH,.
The quantity (cBAA.), may be estimated by one of the following three methods:
(i)
Given
&AA*
at a known temperature and pressure, one can read
(c~AA*)~
from
the chart and get
(&,,*),
=
c%~~*/(c~~~*)~.
R. C. Reid,
J.
M.
Prausnitz, and
B. E.
Poling,
The Properties of Gases and Liquids,
4th edition,
McGraw-Hill, New York (19879, Chapter 11.
E.
N.
Fuller,
P.
D.
Shettler, and
J.
C.
Giddings,
Ind. Eng. Chem.,
58,
No. 5,19-27 (1966); Erratum:
ibid.
58,
No. 8,81 (1966). This paper gives a useful method for predicting binary gas diffusivities from the
molecular formulas of the two species.
J.
C.
Slattery and R.
B.
Bird,
AIChE
Journal,
4,137-142 (1958).
Other correlations for self-diffusivity at elevated pressures have appeared in Ref.
3
and in
L.
S.
Tee, G.
F.
Kuether, R.
C.
Robinson, and
W.
E.
Stewart,
API Proceedings, Division of Refining,
235-243
(1966); R.
C.
Robinson and
W.
E.
Stewart,
IEC Fundamentals,
7,90-95 (1968);
J.
L.
Bueno,
J.
Dizy,
R. Alvarez, and
J.
Coca,
Trans. Insf. Chem. Eng.,
68,
Part
A,
392-397 (1990).
522
Chapter 17 Diffusivity and the Mechanisms of Mass Transport
Fig.
17.2-1.
A
corresponding-
states plot for the reduced
self-diffusivity. Here
(~53~~s)~
=
(p9,,,),
for Ar, Kr, Xe, and
CH,
is plotted as a function of re-
duced temperature for several
values of the reduced pressure.
This chart is based on diffusiv-
ity data of
J.
J.
van Loef and
E.
G.
D.
Cohen, Pkysica
A,
156,
522-533 (1989), the compress-
ibility function of
B.
I.
Lee and
M.
G.
Kesler, AICkE Journal,
21,
510-527 (1975), and
Eq.
17.3-11
for the low-pressure limit.
0.6 0.8 1.0 1.5
2
3
45
Reduced
temperature,
T,
=
T/T,
(ii)
One can predict a value of
&hAA*
in the low-density region by the methods
given in 517.3 and then proceed as in (i).
(iii)
One can use the empirical formula (see Problem 17A.9):
This equation, like Eq. 17.2-1, should not be used for helium or hydrogen isotopes. Here
c
[=I
g-mole/cm3,
9~~~*
[=I
cm2/s,
T,
[=I
K,
and
p,
[=I
atm.
Thus far the discussion of high-density behavior has been concerned with self-diffu-
sion. We turn now to the binary diffusion of chemically dissimilar species. In the absence
of other information it is suggested that Fig. 17.2-1 may be used for crude estimation
of
cg,,, with
pCA
and TcA replaced everywhere by
qpcAF?cB
and
v'Z
respectively (see
Problem 17A.9 for the basis for this empiricism). The ordinate of the plot is then inter-
preted as
(~9~~)~
=
~9~~/(~9~~)~
and Eq. 17.2-2 is replaced by
With these substitutions, accurate results are obtained in the low-pressure limit.
At
higher pressures, very few data are available for comparison, and the method must be
regarded as provisional.
The results in Fig. 17.2-1, and their extensions to binary systems, are expressed in
terms of caAA* and c9,, rather than
9,.
and
BA,.
This is done because the c-multiplied
diffusion coefficients are more frequently required in mass transfer calculations, and
their dependence on pressure and temperature is simpler.

517.2 Temperature and Pressure Dependence of Diffusivities
523
EXAMPLE
17.2-1
Estimation
of
Diffusivity at
Low
Density
EXAMPLE
17.2-2
Estimation
of
Self-
Diffusivity at High
Density
Estimate BAB for the system
CO-C02
at 296.1K and
1
atm total pressure.
SOLUTION
The properties needed for
Eq.
17.2-1 are (see Table E.l):
Label Species
M
T, (K) p, (atm)
Therefore,
Substitution of these values into
Eq.
17.2-1 gives
This gives QAB
=
0.152 cm2/s, in agreement with the experimental value.5 This is unusually
good agreement.
This problem can also be solved by means of Fig. 17.2-1 and
Eq.
17.2-3, together with the
ideal gas law p
=
cRT.
The result is BAB
=
0.140 cm2/s, in fair agreement with the data.
Estimate
c93,qAx
for
C1402
in ordinary C02 at 171.7 atm and 373K. It is known6 that QAA*
=
0,113 cm2/s at 1.00 atm and 298K, at which condition
c
=
p/
RT
=
4.12
X
g-mole/cm3.
SOLUTION
Since a measured value of
9AAX
is given, we use method
(i).
The reduced conditions of the
measurement are
T,
=
298/304.2
=
0.980 and p,
=
1.00/72.9
=
0.014. Then from Fig. 17.2-1 we
get the value (CQ~~)~
=
0.98. Hence
At
the conditions of prediction (T,
=
373/304.2
=
1.23 and p,
=
171.7/72.9
=
2.36), we read
(aAA*),
=
1.21. The predicted value is then
The data of O'Hern and Martin7 give
a,,*
=
5.89
X
g-mole/cm
.
s at these conditions.
This good agreement is not unexpected, inasmuch as their low-pressure data were used in the
estimation of
(dBAA.),.
B.
A.
Ivakin,
P.
E.
Suetin,
Sov. Phys. Tech. Phys.
(English
translation),
8,748-751
(1964).
E.
B.
Wynn,
Phys. Rev.,
80,1024-1027 (1950).
H.
A.
O'Hern
and
J.
J.
Martin,
Ind.
Eng.
Chern.,
47,2081-2086 (1955).

524
Chapter 17 Diffusivity and the Mechanisms of Mass Transport
EXAMPLE
17.2-3
Estimation
of
Bina
y
Difisivity at High
Density
This problem can also be solved by method (iii) without an experimental value of c9,,*.
Equation 17.4-2 gives directly
The resulting predicted value of
&,,.
is 5.1
X
lop6
g-mole/cm
.
s.
Estimate c9,, for a mixture of 80 mole% CH, and 20 mole% C2H6 at 136 atm and 313K. It is
known that, at 1 atm and 293K, the molar density is c
=
4.17
X
g-mole/cm3 and
gAB
=
0.163 cm2/s.
SOLUTION
Figure 17.2-1 is used, with method (i). The reduced conditions for the known data are
From Fig. 17.2-1 at these conditions we obtain
=
1.21. The critical value
(~9,~)~
is
therefore
c9,, (4.17
X
10-~)(0.163)
(&A,),
=
-
- -
(BAB)~
1.21
=
5.62
X
g-mol/cm
.
s
(17.2-10)
Next we calculate the reduced conditions for the prediction
(Tr
=
1.30,
p,
=
2.90) and read the
value (cg,,),
=
1.31 from Fig. 17.2-1. The predicted value of c9,, is therefore
Experimental measurements8 give c9,,
=
6.0
X
so that the predicted value is
23% high. Deviations of this magnitude are not unusual in the estimation of c9,, at high
densities.
An alternative solution may be obtained by method (iii). Substitution into Eq. 17.4-3
gives
Multiplication by (caAB), at the desired condition gives
This is in closer agreement with the measured value.8
V.
J.
Berry,
Jr.,
and
R.
C.
Koeller,
AIChE
Journal,
6,274-280
(1960).

517.3 Theory of Diffusion in Gases at Low Density
525
$17.3
THEORY OF DIFFUSION IN GASES AT LOW DENSITY
The mass diffusivity
BAB
for binary mixtures of nonpolar gases is predictable within
about
5%
by kinetic theory. As in the earlier kinetic theory discussions in 951.4 and 9.3,
we start with a simplified derivation to illustrate the mechanisms involved and then pre-
sent the more accurate results of the Chapman-Enskog theory.
Consider a large body of gas containing molecular species
A
and
A*,
which are iden-
tical except for labeling. We wish to determine the self-diffusivity
9,*
in terms of the
molecular properties on the assumption that the molecules are rigid spheres of equal
mass
m,
and diameter
dA.
Since the properties of
A
and
A*
are nearly the same, we can use the following re-
sults of the kinetic theory for a pure rigid-sphere gas at low density in which the gradi-
ents of temperature, pressure, and velocity are small:
ii
=
@
=
mean molecular speed relative to
u
(17.3-1)
Z
=
inii
=
wall collision frequency per unit area in a stationary gas
(17.3-2)
A
=
=
mean free path
find2n
The molecules reaching any plane in the gas have, on the average, had their last collision
at a distance
a
from the plane, where
2
a
=
$i
(17.3-4)
In these equations
n
is the number density (total number of molecules per unit volume).
To predict the self-diffusivity
BAA*,
we consider the motion of species
A
in the
y
di-
rection under a mass fraction gradient
dw,/dy
(see Fig. 17.3-I), where the fluid mixture
moves in the
y
direction at a finite velocity mass average velocity
vy
throughout. The
temperature
T
and the total molar mass concentration
p
are considered constant. We as-
sume that Eqs. 17.3-1 to 4 remain valid in this nonequilibrium situation. The net mass
flux of species
A
crossing a unit area of any plane of constant
y
is found by writing an
ex-
pression for the mass of
A
crossing the plane in the positive
y
direction and subtracting
the mass of
A
crossing in the negative
y
direction:
Here the first term is the mass transport in the
y
direction because of the mass motion of
the fluid-that is, the convective transport-and the last two terms give the molecular
transport relative to
vy.
Y
Mole-fraction
profile
oA(y)
//
Molecule arriving at
y
after collision at
y
-a.
The fraction of such
\
molecules that are
of
species
A
is
uAl
-
a
Fig.
17.3-1. Molecular transport
of species
A
from the plane at
(y
-
a)
to the plane at
y.
526
Chapter 17 Diffusivity and the Mechanisms of Mass Transport
It is assumed that the concentration profile
wA(y)
is very nearly linear over distances
of several mean free paths. Then we may write
Combination of the last two equations then gives for the combined mass flux at plane
y:
This is the convective
mass
flux plus the molecular mass flux, the latter being given by Eq.
17.1-1. Therefore we get the following expression for the self-diffusivity:
Finally, making use of
Eqs.
17.3-1 and
3,
we get
which can be compared with
Eq.
1.4-9 for the viscosity and Eq. 9.3-12 for the thermal
conductivity.
The development of a formula for
%AB
for rigid spheres of unequal masses and di-
ameters is considerably more difficult. We simply quote the result' here:
That is, l/mA is replaced by the arithmetic average of
l/mA
and l/mB, and dA by the
arithmetic average of
dA
and dB.
The preceding discussion shows how the diffusivity can be obtained by mean free
path arguments. For accurate results the Chapman-Enskog kinetic theory should
be
used. The Chapman-Enskog results for viscosity and thermal conductivity were given
in
551.4
and
9.3,
respectively. The corresponding formula for c9,,
Or,
if
we approximate c by the ideal gas law
p
=
cRT, we get for
9,,
In the second line of Eqs. 17.3-11 and 12,
9JAB
[=]
cm2/s,
OAB
[=I
A,
T
[=I
K,
and
p
[=I
atm.
A
similar result
is
given by
R.
D.
Present,
Kinetic
Theory
of Gases,
McGraw-Hill,
New York
(1958),
p.
55.
S.
Chapman and
T.
G.
Cowling,
The
MathematicaI Theoy
of
Non-Unifovm Gases,
3rd edition,
Cambridge University Press
(19701,
Chapters
10
and
14.
J.
0.
Hirschfelder,
C.
F.
Curtiss, and
R.
B. Bird,
Molecular Theory
of
Gases and Liquids,
2nd corrected
printing, Wiley, New
York
(19641,
p.
539.
