Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena

Подождите немного. Документ загружается.

518.2

Diffusion Through a Stagnant Gas Film

547

Substitution of

Eq.

18.2-1 into

Eq.

18.2-3 gives

For an ideal gas mixture the equation of state is

cRT,

so that at constant temperature

and pressure

must be a constant. Furthermore, for gases

aAB

is very nearly indepen-

dent of the composition. Therefore, can be moved to the left of the derivative opera-

tor to get

This is a second-order differential equation for the concentration profile expressed as

mole fraction of

Integration with respect to

gives

second integration then gives

If we replace

by -In

and

by -In

K,,

Eq. 18.2-7 becomes

The two constants of integration,

and

K,,

may then be determined from the boundary

conditions

B.C.

z,,

xA,

z2,

x~2

When the constants have been obtained,

get finally

The profiles for gas

are obtained by using

x,. The concentration profiles are

shown in Fig. 18.2-1. It can be seen there that the slope dxA/dz is not constant although

is; this could have been anticipated from

Eq.

18.2-1.

Once the concentration profiles are known, we can get average values and mass

fluxes at surfaces. For example, the average concentration of

in the region between

and z, is obtained as follows:

in which

z,)/(z,

z,) is a dimensionless length variable. This average may be

rewritten as

That is, the average value of

is the logarithmic mean, (x,),,, of the terminal concen-

trations.

548

Chapter

Concentration Distributions in Solids and in Laminar Flow

Main fluid stream

in turbulent

flow

Fig.

18.2-2.

Film model for mass transfer; component

is diffusing from the surface into the gas stream through

a hypothetical stagnant gas film.

The rate of mass transfer at the liquid-gas interface-that is, the rate of evapora-

tion-may be obtained from Eq. 18.2-1 as follows:

By combining Eqs. 18.2-13 and 14 we get finally

This expression gives the evaporation rate in terms of the characteristic driving force

XAl

x~2.

By expanding the solution in

Eq.

18.2-15 in a Taylor series, we can get (see 5C.2 and

Problem 18B.18)

The expression in front of the bracketed expansion is the result that one would get if the

convection term were entirely omitted in Eq. 18.0-1. The bracketed expansion then gives

the correction resulting from including the convection term. Another way of interpreting

this expression is that the simple result corresponds to joining the end points of the

curve in Fig. 18.2-1 by a straight line, and the complete result corresponds to using the

curve of

versus

If the terminal mole fractions are small, the correction term in brack-

ets in Eq. 18.2-16 is only slightly greater than unity.

The results of this section have been used for experimental determinations of gas

diffusivities.' Furthermore, these results find use in the "film models" of mass transfer.

In Fig. 18.2-2 a solid or liquid surface is shown along which a gas is flowing. Near the

surface is a slowly moving film through which

diffuses. This film is bounded by the

surfaces

and

In this "model" it is assumed that there is a sharp transition

from a stagnant film to a well-mixed fluid in which the concentration gradients are negli-

gible. Although this model is physically unrealistic, it has nevertheless proven useful as

a simplified picture for correlating mass transfer coefficients.

Lee

and

Wilke,

Ind.

Eng.

Chem.,

46,2381-2387

(1954).

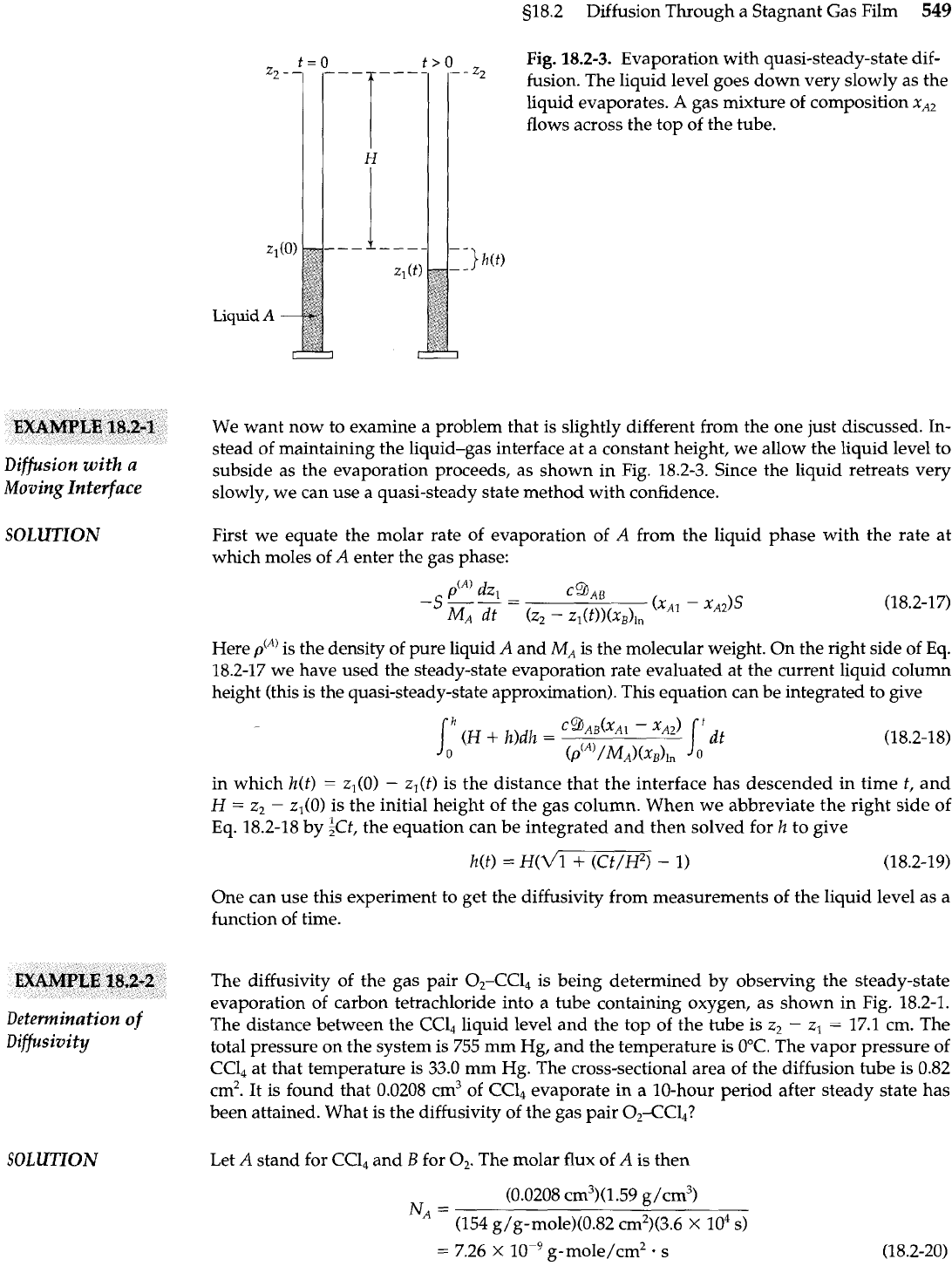
s18.2 Diffusion Through a Stagnant Gas Film

549

Fig.

18.2-3.

Evaporation with quasi-steady-state dif-

fusion. The liquid level goes down very slowly as the

liquid evaporates.

gas mixture of composition

xA2

flows across the top of the tube.

Liquid

We want now to examine a problem that is slightly different from the one just discussed. In-

stead of maintaining the liquid-gas interface at a constant height, we allow the liquid level to

Diffusion

with

subside as the evaporation proceeds, as shown in Fig. 18.2-3. Since the liquid retreats very

Moving Interface

slowly, we can use a quasi-steady state method with confidence.

SOLUTION

First we equate the molar rate of evaporation of

from the liquid phase with the rate at

which moles of

enter the gas phase:

Here

p(A'

is the density of pure liquid

and

is the molecular weight. On the right side of Eq.

18.2-17 we have used the steady-state evaporation rate evaluated at the current liquid column

height (this is the quasi-steady-state approximation). This equation can be integrated to give

in which

h(t)

zl(0)

z,(t) is the distance that the interface has descended in time

and

q(0) is the initial height of the gas column. When we abbreviate the right side of

Eq. 18.2-18 by iCt, the equation can be integrated and then solved for

to give

One can use this experiment to get the diffusivity from measurements of the liquid level as a

function of time.

Determination of

Diffusivity

The diffusivity of the gas pair 0,-CC1, is being determined by observing the steady-state

evaporation of carbon tetrachloride into a tube containing oxygen, as shown in Fig. 18.2-1.

The distance between the

CCl,

liquid level and the top of the tube is

17.1 cm. The

total pressure on the system is 755 mm Hg, and the temperature is 0°C. The vapor pressure of

CCl, at that temperature is 33.0 mm Hg. The cross-sectional area of the diffusion tube is 0.82

cm2. It is found that 0.0208 cm3 of CCl, evaporate in a 10-hour period after steady state has

been attained. What is the diffusivity of the gas pair 02-CCl,?

SOLUTION

Let

stand for CCl, and

for

02.

The molar flux of

is then

550

Chapter 18

Concentration Distributions in Solids and in Laminar Flow

Then from Eq. 18.2-14 we get

This method of determining gas-phase diffusivities suffers from several defects: the cooling

of the liquid by evaporation, the concentration of nonvolatile impurities at the interface, the

climbing of the liquid up the walls of the tube, and the curvature of the meniscus.

(a)

Derive expressions for diffusion through a spherical shell that are analogous to Eq. 18.2-11

(concentration profile) and

Eq.

18.2-14 (molar flux). The system under consideration

shown

Diffusion through a

in pin.

18.2-4.

Nonisothermal

Spherical Film

SOLUTION

(b)

Extend these results to describe the diffusion in a nonisothermal film in which the tem-

perature varies radially according to

where

is the temperature at

r,.

Assume as

rough

approximation that

varies as the

$-power of the temperature:

in which is the diffusivity at

TI.

Problems of this kind arise in connection with dry-

ing of droplets and diffusion through gas films near spherical catalyst pellets.

The temperature distribution in Eq. 18.2-22 has been chosen solely for mathematical sim-

plicity. This example is included to emphasize that, in nonisothermal systems, Eq. 18.0-1 is

the correct starting point rather than NAz

-gAB(dcA/dz)

xA(NAz

NBz),

as has been given

some textbooks.

(a)

A steady-state mass balance on a spherical shell leads to

Fig.

18.2-4.

Diffusion through a hypotheti-

cal spherical stagnant gas film surrounding

a droplet of liquid

918.3 Diffusion with a Heterogeneous Chemical Reaction

551

We now substitute into this equation the expression for the molar flux NAr, with

NB,

set equal

to zero, since

is insoluble in liquid

his-gives

For

constant temperature

the product

c9AB

is constant, and

Eq.

give the concentration distribution

From Eq. 18.2-26 we can then get

(18.2-25)

18.2-25 may be integrated to

which is the molar flow of

across any spherical surface of radius

between

and

r,.

(b)

For the nonisothermal problem, combination of Eqs. 18.2-22 and 23 gives the variation of

diffusivity with position:

When this expression is inserted into

Eq.

18.2-25 and

is set equal to p/RT, we get

After integrating between

and

r,,

we obtain (for

-2)

For

0, this result simplifies to that in Eq. 18.2-27.

518.3

DIFFUSION WITH A HETEROGENEOUS

CHEMICAL REACTION

Let us now consider a simple model for a catalytic reactor, such as that shown in Fig.

18.3-la, in which a reaction

is being carried out. An example of a reaction of this

type would be the solid-catalyzed dimerization of

CH,CH

CH,.

We imagine that each catalyst particle is surrounded

a stagnant gas film

through which

has to diffuse to reach the catalyst surface, as shown in Fig. 18.3-lb

At the catalyst surface we assume that the reaction

occurs instantaneously,

and that the product

then diffuses back out through the gas film to the main turbu-

lent stream composed of

and

We want to get an expression for the local rate of

conversion from

when the effective gas-film thickness and the main stream

concentrations

x,,,

and

x,,

are known. We assume that the gas film is isothermal, al-

though in many catalytic reactions the heat generated by the reaction cannot be

neglected.

For the situation depicted in Fig. 18.3-lb, there is

one

mole of

moving in the

minus

direction for every

two

moles of

moving in the

plus

direction. We know this from

the stoichiometry of the reaction. Therefore we know that at steady state

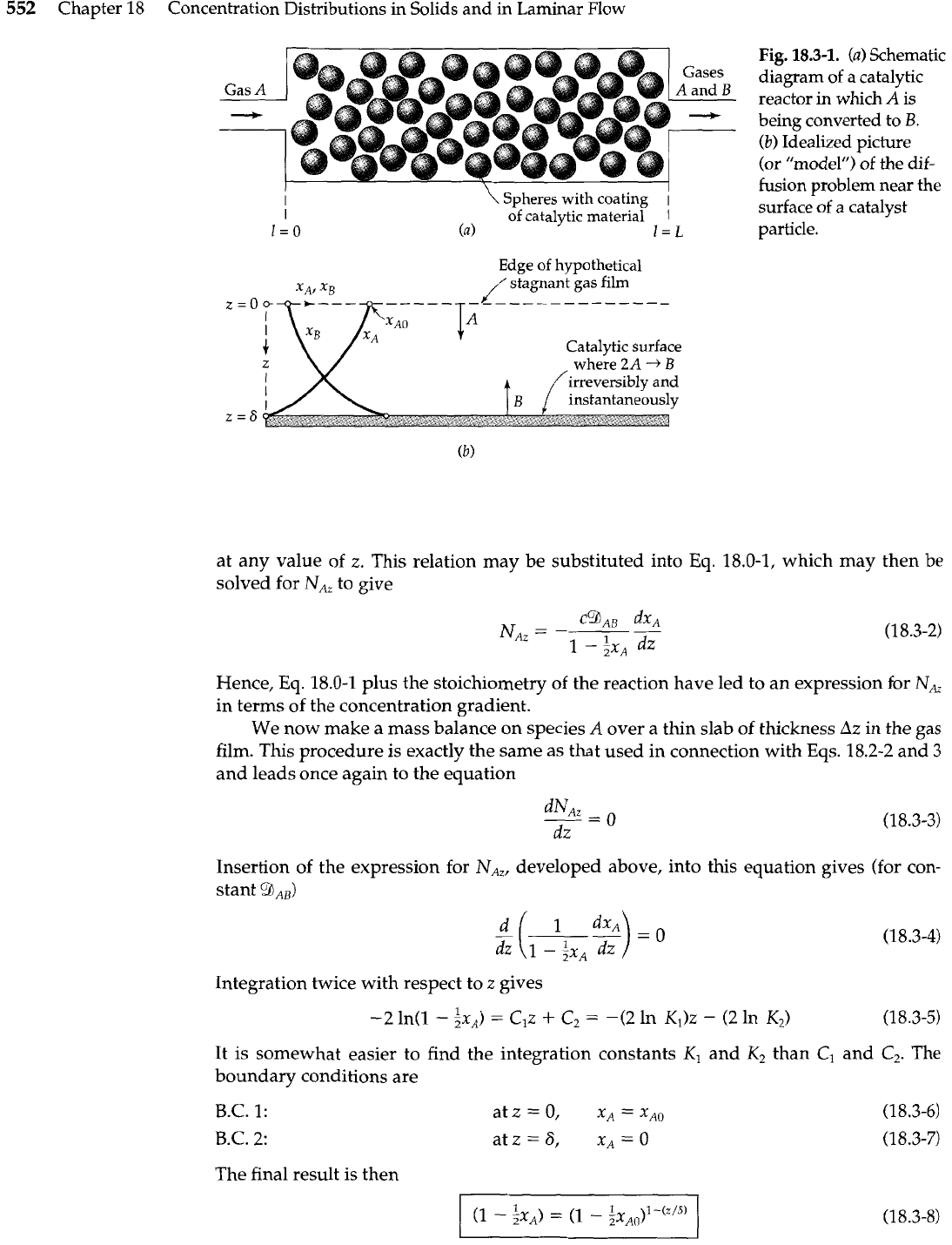
552

Chapter 18 Concentration Distributions in Solids and in Laminar Flow

Gas

Gases

and

-f

Spheres with coating

of catalytic material

(a)

I=L

Edge

hypothetical

stagnant

gas

film

Fig.

18.3-1.

(a)

Schematic

diagram of a catalytic

reactor in which

being converted to

(b)

Idealized picture

(or

"rn~clel'~)

the dif-

fusion problem near the

surface of a catalyst

particle.

at any value of

This relation may be substituted into Eq. 18.0-1, which may then be

solved for

NAZ

to give

Hence, Eq. 18.0-1 plus the stoichiometry of the reaction have led to an expression for

in terms of the concentration gradient.

We now make a mass balance on species

over a thin slab of thickness

in the

gas

film. This procedure is exactly the same as that used in connection with Eqs. 18.2-2 and

and leads once again to the equation

Insertion of the expression for NAt, developed above, into this equation gives (for con-

stant

%,,)

Integration twice with respect to

gives

It is somewhat easier to find the integration constants

and

than

and

C2.

The

boundary conditions are

B.C.

The final result is then

s18.3 Diffusion with a Heterogeneous Chemical Reaction

553

for the concentration profile in the gas film. Equation 18.3-2 may now be used to get the

molar flux of reactant through the film:

The quantity

may also be interpreted as the local rate of reaction per unit area of cat-

alytic surface. This information can be combined with other information about the cat-

alytic reactor sketched in Fig.

18.3-l(a)

to get the overall conversion rate in the entire

reactor.

One point deserves to be emphasized. Although the chemical reaction occurs instan-

taneously at the catalytic surface, the conversion of

proceeds at a finite rate

be-

cause of the diffusion process, which is "in series" with the reaction process. Hence we

speak of the conversion of

as being difision controlled.

In the example above we have assumed that the reaction occurs instantaneously at

the catalytic surface. In the next example we show how to account for finite reaction ki-

netics at the catalytic surface.

Rework the problem just considered when the reaction

is not instantaneous at the cat-

alytic surface at

6. Instead, assume that the rate at which

disappears at the catalyst-

with

coated surface is proportional to the concentration of

in the fluid at the interface,

Heterogeneous

Reaction

NAz

k;cA

k;cxA (18.3-10)

in which

is a rate constant for the pseudo-first-order surface reaction.

SOLUTION

We proceed exactly as before, except that B.C.

in Eq. 18.3-7 must be replaced by

B.C.

2':

NA,

being, of course, a constant at steady state. The determination of the integration constants

from B.C. 1 and

B.C.

leads to

From this we evaluate (dxA/dz)l,=, and substitute it into Eq. 18.3-2, to get

This is a transcendental equation for NAz as a function of xA,,

k;,

&IAB, and

When

is large,

the logarithm of 1

:(~,,/k:c) may be expanded in a Taylor series and all terms discarded

but the first. We then get

NA~

2c9~d6

in(

)

(k,

large) (18.3-14)

9,,/k;'~

PA,

Note once again that we have obtained the rate of the combined reaction and diffusion process.

Note also that the dimensionless group 9A,/k;6 describes the effect of the surface reaction ki-

netics on the overall diffusion-reaction process. The reciprocal of this group is known as the

second Damkohler number' Da"

k;6/gA,. Evidently we get the result in

Eq.

18.3-9 in the limit

Dan

Damhohler,

Elektrochem.,

42,846-862

(1936).

554

Chapter

Concentration Distributions in Solids and in Laminar Flow

Gas

Fig.

18.4-1.

Absorption of

with a

homogeneous reaction in the liquid phase.

518.4

DIFFUSION WITH A HOMOGENEOUS

CHEMICAL REACTION

As the next illustration of setting up a mass balance, we consider the system shown in

Fig. 18.4-1. Here gas

dissolves in liquid

in a beaker and diffuses isothermally into the

liquid phase. As it diffuses, A also undergoes an irreversible first-order homogeneous

re-

action:

AB.

An example of such a system is the absorption of CO, by a concen-

trated aqueous solution

NaOH.

We treat this as a binary solution of

and

ignoring the small amount of AB that is

present (the

pseudobinay assumption).

Then the mass balance on species

over a thick-

ness

of the liquid phase becomes

in which

kq'

is a first-order rate constant for the chemical decomposition of A, and

is the

cross-sectional area of the liquid. The product

kq'cA

represents the moles of

consumed

by the reaction per unit volume per unit time. Division of Eq. 18.4-1 by

SAz

and taking

the limit as

gives

If the concentration of

is small, then we may to

good approximation write Eq. 18.0-1 as

since the total molar concentration

is virtually uniform throughout the liquid. Combin-

ing the last two equations gives

This is to be solved with the following boundary conditions:

B.C.

C~O

NA,

(or

dcn/dz

The first boundary condition asserts that the concentration of A at the surface in the liq-

uid remains at a fixed value

c,,.

The second states that no A diffuses through the bottom

of the container at

Eq. 18.4-4 is multiplied by

then it can be written in dimensionless vari-

ables in the form of Eq. C.l-4

s18.4

Diffusion with a Homogeneous Chemical Reaction

555

where

cA/cAO

is a dimensionless concentration,

z/L

a dimensionless length,

and

k;"L2/91AB

dimensionless group, known as the

Thiele modulus.'

This group

represents the relative influence of the chemical reaction

kycAO

and diffusion

c~~~~~/L~.

Equation 18.4-7 is to be solved with the dimensionless boundary conditions that at

1, and at

dr/dc

The general solution is

cosh

sinh

(18.4-8)

When the constants of integration are evaluated, we get

cosh

sinh

cosh[+(l

5)1

(18.4-9)

cosh

Then reverting to the original notation

The concentration profile thus obtained is plotted in Fig. 18.4-1.

Once we have the complete concentration profile, we may evaluate other quantities,

such as the average concentration in the liquid phase

Also, the molar

flux

at the plane

can be found to be

This result shows how the chemical reaction influences the rate of absorption of gas

liquid

The reader may wonder how the solubility

cAo

and the diffusivity

QAB

can be de-

termined experimentally if there is a chemical reaction taking place. First,

can

be measured in a separate experiment in a well-stirred vessel. Then, in principle,

cAO

and

9AR

can be obtained from the measured absorption rates for various liquid

depths

Estimate the effect of chemical reaction rate on the rate of gas absorption in an agitated tank

(see Fig.

18.4-2).

Consider a system in which the dissolved gas

undergoes an irreversible

Gas

with

first

order reaction with the liquid

that is,

disappears within the liquid phase at a rate

Chemical Reaction

proportional to the local concentration of

An example of such a system is the absorption of

Agitated Tank2

SO, or

H2S

in aqueous NaOH solutions.

Thiele,

Ind.

Eng.

Chem.,

31,916-920 (1939).

Ernest William Thiele

(pronounced "tee-lee")

(1895-1993) is noted for his work on catalyst effectiveness factors and his part in the development

the

"McCabe-Thiele" diagram. After 35 years with Standard Oil of Indiana, he taught for a decade at Notre

Dame University.

Lightfoot,

AIChE

Journal,

4,499-500 (1958), 8,710-712 (1962).

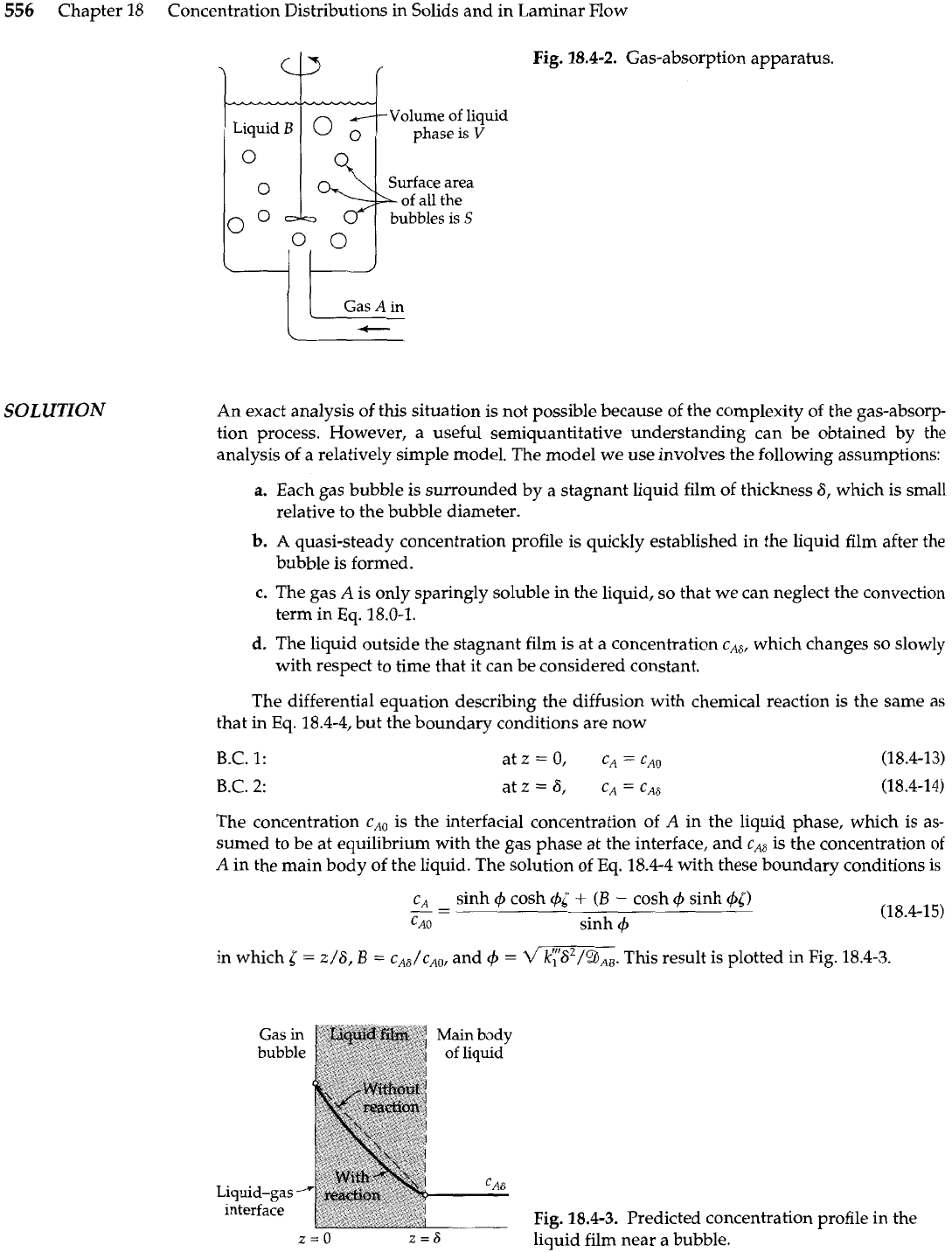
556

Chapter 18 Concentration Distributions in Solids and in

SOLUTION

Surface area

all the

bubbles is

Laminar Flow

Fig.

18.4-2.

Gas-absorption apparatus.

An exact analysis of this situation is not possible because of the complexity of the gas-absorp-

tion process. However, a useful semiquantitative understanding can be obtained by the

analysis of a relatively simple model. The model we use involves the following assumptions:

Each gas bubble is surrounded by a stagnant liquid film of thickness

which is small

relative to the bubble diameter.

quasi-steady concentration profile is quickly established in the liquid film after the

bubble is formed.

The gas

is only sparingly soluble in the liquid, so that we can neglect the convection

term in

Eq.

18.0-1.

The liquid outside the stagnant film is at a concentration

CA&

which changes so slowly

with respect to time that it can be considered constant.

The differential equation describing the diffusion with chemical reaction is the same

that in

Eq.

18.4-4, but the boundary conditions are now

B.C. 1:

B.C.

The concentration

cA,

is the interfacial concentration of

in the liquid phase, which is as-

sumed to be at equilibrium with the gas phase at the interface, and

cA,

is the concentration

in the main body of the liquid. The solution of Eq. 18.4-4 with these boundary conditions is

sinh

cosh

sinh

4[)

CAO

sinh

(18.4-15)

in which

z/S,

cA8/cA0,

and

k',"6'/aAB.

This result is plotted in Fig. 18.4-3.

Gas in

bubble

Liquid-gas

interface

Main body

liquid

C~~

Fig.

18.4-3.

Predicted concentration profile in the

liquid film near

bubble.