Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena
Подождите немного. Документ загружается.


Chapter
21
Concentration Distributions
in Turbulent
Flow
521.1
Concentration fluctuations and the time-smoothed concentration
521.2
Time-smoothing of the equation of continuity of
A
521.3
Semi-empirical expressions for the turbulent mass flux
521.4'
Enhancement of mass transfer by a first-order reaction in turbulent
flow
521.5.
Turbulent mixing and turbulent flow with second-order reaction
In preceding chapters we have derived the equations for diffusion
in
a fluid or solid, and
we have shown how one can obtain expressions for the concentration distribution, pro-
vided no fluid turbulence is involved. Next we turn our attention to mass transport in
turbulent flow.
The discussion here is quite similar to that in Chapter 13, and much of that material
can be taken over by analogy. Specifically, 5513.4, 13.5, and 13.6 can be taken over di-
rectly by replacing heat transfer quantities by mass transfer quantities. In fact, the prob-
lems discussed in those sections have been tested more meaningfully in mass transfer,
since the range of experimentally accessible Schmidt numbers is considerably greater
than that for Prandtl numbers.
We restrict ourselves here to isothermal binary systems, and make the assumption
of constant mass density and diffusivity. Therefore the partial differential equation de-
scribing diffusion
in
a flowing fluid (Eq. 19.1-16) is of the same form as that for heat con-
duction in a flowing fluid (Eq. 11.2-9), except for the inclusion of the chemical reaction
term in the former.
,1
CONCENTRATION FLUCTUATIONS AND
THE TIME-SMOOTHED CONCENTRATION
The discussion in 513.1 about temperature fluctuations and time-smoothing can be taken
over by analogy for the molar concentration c,. In a turbulent stream, c, will be a rapidly
oscillating function that can be written as the sum of a time-smoothed value
ZA
and a tur-
bulent concentration fluctuation c:
which is analogous to Eq. 13.1-1 for the temperature.
--
By
virtue of the definition of c; we
see that
=
0.
However, quantities such as vick, v$;, and
a
are not zero, because the
local fluctuations in concentration and velocity are not independent of one another.
The time-smoothed concentration profiles
G(x,
y,
z,
t)
are those measured, for exam-
ple, by the withdrawal of samples from the fluid stream at various points and various

658
Chapter 21 Concentration Distributions in Turbulent Flow
times. In tube flow with mass transfer at the wall, one expects that the time-smoothed
concentration
CA
will vary only slightly with position in the turbulent core, where the
transport by turbulent eddies predominates. In the slowly moving region near the bound-
ary surface, on the other hand, the concentration
%
will be expected to change within a
small distance from its turbulent-core value to the wall value. The steep concentration
gradient is then associated with the slow molecular diffusion process in the viscous sub-
layer in contrast to the rapid eddy transport in the turbulent core.
521.2
TIME-SMOOTHING OF THE EQUATION
OF CONTINUITY OF
A
We begin with the equation of continuity for species
A,
which we presume is disappearing
by an nth-order chemical reaction.' Equation 19.1-16 then gives, in rectangular coordinates,
Here
kr
is the reaction rate coefficient for the nth-order chemical reaction, and is pre-
sumed to be independent of position. In subsequent equations we shall consider n
=
1
and n
=
2 to emphasize the difference between reactions of first and higher order.
When cA is replaced by
&
+
c;, and
vi
by
Ei
+
ul!, we obtain after time-averaging
Comparison of this equation with Eq. 21.2-1 indicates that the time-smoothed equation
differs in the appearance
-
of some extra terms, marked here with dashed underlines.
The
terms containing vlc; describe the turbulent mass transport and we designate them by
FA!,
the ith component of the turbulent molar flux vector. We have now met the third of
the turbulent fluxes, and we may summarize their components thus:
-
-
turbulent molar flux (vector)
Ti;
=
ui c; (21.2-3)
-
-
turbulent momentum flux (tensor)
.$)
=
Pv;v;
(21.2-4)
-
turbulent heat flux (vector)
4i
ct)
-
-P
c
v!~t
(21.2-5)
All of these are defined as fluxes with respect to the mass average velocity.
It is interesting to note that there is an essential difference between the behaviors of
chemical reactions of different orders. The first-order reaction has the same form
in
the
time-smoothed equation as in the original equation. The second-order reaction, on the
other hand, contributes on time-smoothing an extra term
-k;"c,
this being the manifes-
tation of the interaction between the chemical kinetics and the turbulent fluctuations.
We now summarize all three of the time-smoothed equations of change for turbu-
lent flow of an isothermal, binary fluid mixture with constant p,
gA,,
and
p:
continuity
(V
-5)
=
0
(21.2-6)
motion
continuity of
A
Here
J$)
=
and it is understood that the op'erator
DIE
is to be written with the
time-smoothed velocity
V
in it.
S.
Corrsin,
Physics
of
Fluids,
1,4247
(1958).

521.4
Enhancement of Mass Transfer
by
a First-Order Reaction in Turbulent Flow
659
521.3
SEMI-EMPIRICAL EXPRESSIONS FOR
THE TURBULENT MASS FLUX
In the preceding section we showed that the time-smoothing of the equation of conti-
I I
nuity of A gives rise to a turbulent mass flux, with components
7;;
=
G.
To solve
mass transport problems in turbulent flow, it may be useful to postulate a relation be-
tween
2;
and the time-smoothed concentration gradient.
A
number of empirical expres-
sions can be found in the literature, but we present here only the two most popular ones.
Eddy Diffusivity
By analogy with Fick's first law of diffusion, we may write
as the defining equation for the
turbulent diffusivity
@&,
also called the
eddy diffusivity.
As
is the case with the eddy viscosity and the eddy thermal conductivity, the eddy diffusiv-
ity is not a physical property characteristic of the fluid, but depends on position, direc-
tion, and the nature of the flow field.
The eddy diffusivity
92)B
and the eddy kinematic viscosity
v"'
=
p't'/p
have the same
dimensions-namely, length squared divided by time. Their ratio
is a dimensionless quantity, known as the
turbulent Schmidt
number.
As is the case with
the turbulent Prandtl number, the turbulent Schmidt number is of the order of unity
(see the discussion in 513.3). Thus the eddy diffusivity may be estimated by replacing it
by the turbulent kinematic viscosity, about which a fair amount is known. This is done
in 921.4, which follows.
The
Mixing-Length Expression of Prandtl
and
Taylor
According to the mixing-length theory of Prandtl, momentum, energy, and mass are all
transported by the same mechanism. Hence by analogy with Eqs. 5.4-4 and 13.3-3 we
may write
where
I
is the Prandtl mixing length introduced in Chapter
5.
The quantity
121
dE,/dyl
ap-
pearing here corresponds to
9zL
of
Eq.
21.3-1, and to the expressions for
v'"
and
a'"
im-
plied by Eqs. 5.4-4 and 13.3-3. Thus, the mixing-length theory satisfies the
Reynolds
annIogy
v(f)
=
=
9")
AB,
or ~r'~)
=
SC")
=
1.
521.4
ENHANCEMENT OF MASS TRANSFER
BY
A FIRST-ORDER
REACTION IN TURBULENT FLOW'
We now examine the effect of the chemical reaction term in the turbulent diffusion equa-
tion. Specifically we study the effect of the reaction on the rate of mass transfer at the
wall for steadily driven turbulent flow in a tube, where the wall (of material A) is slightly
'
0.
T.
Hanna,
0.
C.
Sandall, and
C.
L.
Wilson,
Ind.
Eng.
Chem. Research,
26,2286-2290 (1987).
An
analogous problem dealing
with
falling films is given
by
0.
C.
Sandall,
0.
T.
Hanna, and
F.
J.
Valeri,
Chem. Eng. Communications,
16,135-147 (1982).

660
Chapter 21 Concentration Distributions in Turbulent Flow
soluble in the fluid (a liquid
B)
flowing through the tube. Material
A
dissolves in liquid
B
and then disappears by a first-order reaction. We shall be particularly interested in the
behavior with high Schmidt numbers and rapid reaction rates.
For tube flow with axial symmetry and with
EA
independent of time,
Eq.
21.2-8
becomes
Here we have made the customary assumption that the axial transport by both molecu-
lar and turbulent diffusion can be neglected. We want to find the mass transfer rate at
the wall
where
CA~
and are the concentrations of
A
at the wall and at the tube axis.
As
pointed out
in
the preceding section, the turbulent diffusivity is zero at the wall, and
consequently does not appear in Eq. 21.4-2. The quantity
kc
is a
mass transfer
coefficient,
analogous to the heat transfer coefficient
h.
The coefficient
h
was discussed in Chapter
14
and mentioned in Chapter
9
in connection with "Newton's law of cooling." As
a
first ap-
proximation' we take to be zero, assuming that the reaction is sufficiently rapid
that the diffusing species never reaches the tube axis; then dZA/dr must also be zero at
the tube axis. After analyzing the system under this assumption, we will relax the as-
sumption and give computations for a wider range of reaction rates.
We now define the dimensionless reactant concentration C
=
ZA/cA0. Then under
the further assumption' that, for large
z,
the concentration will be independent of
z,
Eq. 21.4-1 becomes
This equation may now be multiplied by r and integrated from an arbitrary position to
the tube wall to give
Here the boundary conditions at r
=
0
have been used, as well as the definition of the
mass transfer coefficient. Then a second integration from
r
=
0
to
r
=
R gives
Here we have used the boundary conditions C
=
0
at r
=
0
and C
=
1
at
r
=
R.
Next we introduce the variable
y
=
R
-
r, since the region of interest
is
right next to
the wall. Then we get
in which C(y) is not the same function of
iJi
as C(7) is of
7.
For large Sc the integrands are
important only in the region where
y
<<
R, so that
R
-
y
may be safely approximated
by R. Furthermore, we can use the fact that the turbulent diffusivity in the neighborhood

g21.4
Enhancement of Mass Transfer by a First-Order Reaction in Turbulent Flow
661
of the wall is proportional to the third power of the distance from the wall. When the in-
tegrals are rewritten in terms of
a
=
y/R, we get the dimensionless equation
This equation contains several dimensionless groupings: the Schmidt number Sc
=
v/9,,,
a dimensionless reaction-rate parameter
Rx
=
k;"R2/v, and a dimensionless mass transfer
coefficient Sh
=
k,D/gAB known as the Sherwood number
(D
being the tube diameter).
In the limit that Rx
+
m,
the solution to Eq. 21.4-3 under the given boundary condi-
tions is
C
=
exp(-Shu/2). Substitution of this solution into Eq. 21.4-7 then gives after
straightforward integration
in which
This can
be
solved' to give Sh as a function of Sc, Rx, and
K.
The foregoing solution of Eq. 21.4-3 is reasonable when Sc,
Rx,
and
z
are sufficiently
large, and is an improvement over the result given by Vieth, Porter and Sherwo~d.~
However, in the absence of chemical reaction,
Eq.
21.4-3 fails to describe the downstream
increase of
C
caused by the transfer of species
A
into the fluid. Thus, the mass-transfer
enhancement by the chemical reaction cannot be assessed realistically from the results of
either Ref.
1
or Ref. 2.
For a better analysis of the enhancement problem, we use Eq. 21.4-1 to get a more
complete differential equation for
C:
The assumption that C
=
0
at r
=
0
is then replaced by the zero-flux condition dC/dr
=
0
there. We represent
'3:b
in this geometry as
l2
IdEJdrl for fully developed flow, by use of
a position-dependent mixing length
1
as in Eq. 21.3-3. Introducing dimensionless nota-
tions
v+
=
EJv,,
z+
=
zv,/v, r+
=
rv,/v, and
It'
=
lv,/v based on the friction velocity
v,
=
of 95.3, we can then express Eq. 21.4-11 in the dimensionless form
in which a Damkohler number Da
=
kyv/v$ has been introduced.
An excellent model for the mixing length
1
is available in Eq. 5.4-7, developed by
Hanna, Sandall, and Mazet3 by
modifying
the model given by van Drie~t.~ This model
--
W.
R.
Vieth,
J.
H.
Porter, and T.
K.
Sherwood,
Ind.
Eng.
Chem.
Fundam.,
2,l-3 (1963).
%.
T.
Hanna,
0.
C.
Sandall, and
P.
R.
Mazet,
AKhE
Journal,
27,693-697 (1981).
E.
R.
van
Driest,
1.
Aero.
Sci.,
23,1007-1011,1036 (1956).
662
Chapter 21 Concentration Distributions in Turbulent Flow
will give smooth concentration profiles, provided that we use a velocity function with
continuous radial derivative, rather than the piecewise continuous expressions given in
Fig. 5.5-3. Such a function is obtainable by integrating the differential equation
in the dimensionless variables
u+
=
&/u,
and
y+
=
yvJv
of Fig. 5.5-3, with the bound-
ary conditions
uf
=
0 at
y+
=
0 (the wall) and
du+/dy+
=
0
at
y+
=
R+
(the centerline).
Equation 21.4-13 is obtained (see Problem 21B.5) by combining the cylindrical-coordinate
versions of Eqs. 5.5-3 and 5.4-4 with the dimensionless form
of the mixing-length model shown in Eq. 5.4-7. Equation 21.4-13 is solvable via the qua-
dratic formula to give
and
v+
is then computable by quadrature using, for example, the subroutines trapzd and
qtrap of Press et aL5 The resulting
v+
function closely resembles the plotted line in Fig.
5.5-3, with small changes near
y'
=
30 where the plotted line has a slope discontinuity,
and near the centerline where the calculated
v+
function attains a maximum value de-
pendent on the dimensionless wall radius
R+
whereas the line in Fig. 5.5-3 improperly
does not.
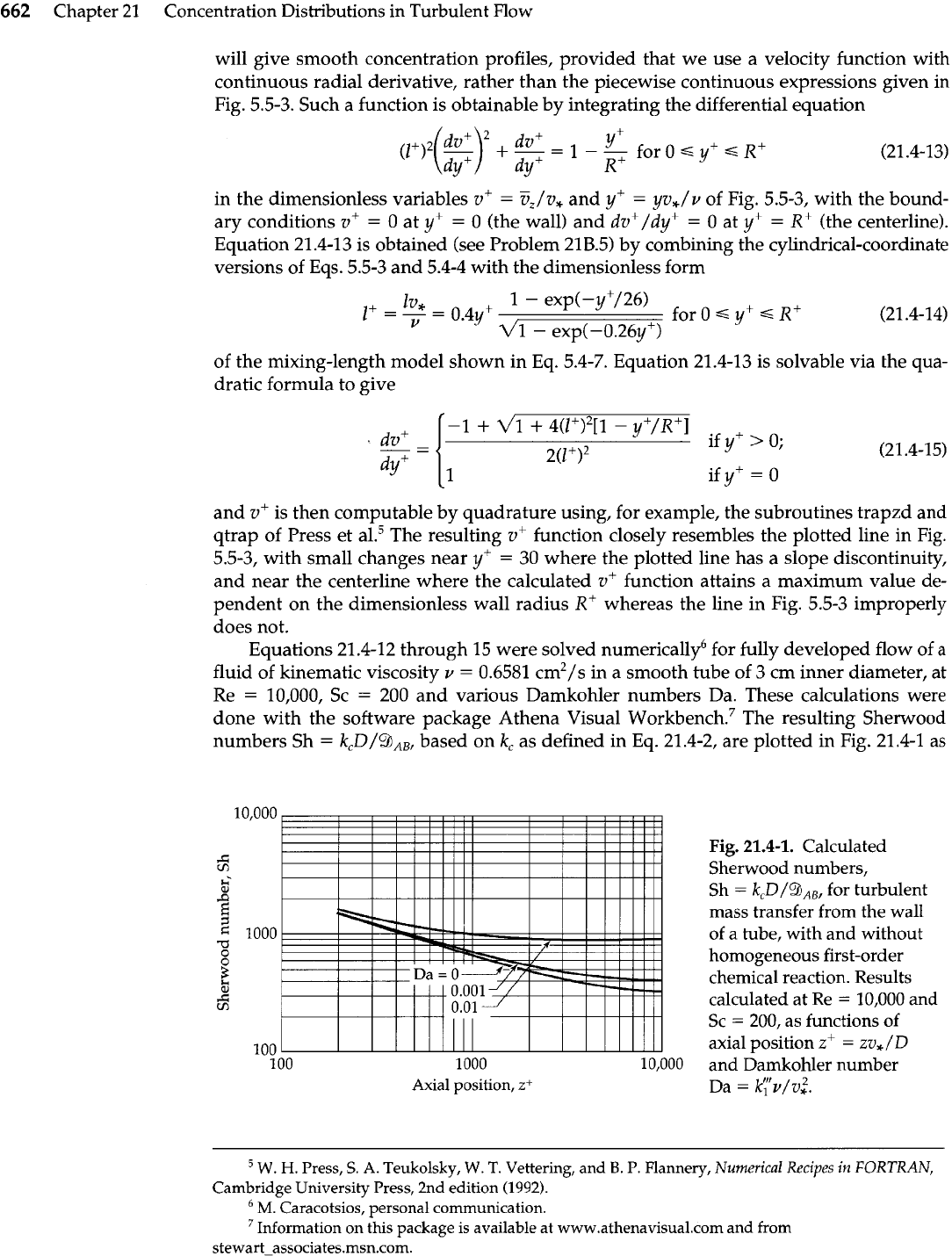
Equations 21.4-12 through 15 were solved numerically6 for fully developed flow of
a
fluid of kinematic viscosity
v
=
0.6581 cm2/s in a smooth tube of 3 cm inner diameter, at
Re
=
10,000, Sc
=
200 and various Damkohler numbers
Da.
These calculations were
done with the software package Athena Visual W~rkbench.~ The resulting Sherwood
numbers Sh
=
kcD/9,,, based on
kc
as defined in Eq. 21.4-2, are plotted in Fig. 21.4-1 as
Axial position,
zi
Fig.
21.4-1.
Calculated
Sherwood numbers,
Sh
=
k,D/QAB,
for turbulent
mass transfer from the wall
of a tube, with and without
homogeneous first-order
chemical reaction. Results
calculated at Re
=
10,000 and
Sc
=
200, as functions of
axial position
zf
=
zv,/D
and Damkohler number
Da
=
kyv/v:.
W.
H.
Press,
S.
A.
Teukolsky,
W.
T.
Vettering, and
B.
P. flannery,
Numerical
Recipes
in
FORTRAN,
Cambridge University Press, 2nd edition
(1992).
M.
Caracotsios, personal communication.
Information on this package is available at www.athenavisual.com and from
stewart~associates.msn.com.

521.5
Turbulent Mixing and Turbulent Flow with Second-Order Reaction
663
functions of
z+
for various values of the Damkohler number Da. These results lead to the
following conclusions:
1.
In the absence of reaction (that is, when Da
=
O),
the Sherwood number falls off
rapidly with increasing distance into the mass-transfer region. This behavior is
consistent with the results of Sleicher and
ribu us'
for a corresponding heat trans-
fer problem, and confirms that the convection term of
Eq.
21.4-11 is essential for
this system. This term was neglected in References
2
and 3 by regarding the con-
centration profiles as "fully developed."
2.
In the presence of a pseudo-first-order homogeneous reaction of the solute (that is,
when Da
>
O),
the Sherwood number falls off downstream less rapidly, and ulti-
mately attains a constant asymptote that depends on the Damkohler number.
Thus, the enhancement factor, defined as Sh (with reaction)/Sh (without reaction),
can increase considerably with increasing distance into the mass-transfer region.
g21.5
TURBULENT MIXING AND TURBULENT
FLOW WITH SECOND-ORDER REACTION
We now consider processes occurring within turbulent fluid systems, with particular ref-
erence to the two mixers shown in Fig. 12.5-1. In Fig. 12.5-l(a) is shown a steady state sys-
fem,
in which two input streams enter a system of fixed geometry at constant rates, and
in Fig. 12.5-l(b) an unsteady state system, in which two initially stationary, segregated,
miscible fluids are mixed by turning an impeller at a constant angular velocity, starting at
time t
=
0.
One stream [in (a)] or one initial region [in (b)] contains solute
A
in solvent
S,
and the other contains solute
B
in solvent
S.
All solutions are sufficiently dilute that the
solutes do not appreciably affect the viscosity, density, or species diffusivities. Then the
behavior of the solute (A or
B)
in either system [(a) or (b)] is described by the non-time-
smoothed diffusion equations
with suitable initial and boundary conditions.
For these systems, we may write that at
z
=
0
[in (a)] or t
=
0 [in
(b)]
C,
=
C,O
and
c,
=
0 (21.5-3,4)
over the A inlet port [in (a)] or the initial region [in (b)], and
C,
=
cBO
and
c,
=
0 (21.5-5,6)
over the
B
inlet port [in (a)] or the initial region [in
(b)].
In addition, we consider all con-
fining surfaces to be inert and impenetrable.'
No Reaction Occurring
For this situation, the terms
RA
and
RB
are identically zero. We now define a single new
independent variable
C.
A.
Sleicher and
M.
Tribus,
Trans.
ASME,
79,789-797
(1957).
In system
(a),
these boundary conditions are only approximations.
The
indicated values of
c~
and
c,
are regarded as asymptotic values for
z
<<
0.

664
Chapter
21
Concentration Distributions
in
Turbulent Flow
Then both Eqs. 21.5-1 and 2 take the following form over the whole system:
Here the subscript i can represent either solute A or solute
B,
and
r
=
0
for (a) the entering A-rich stream, or
(b)
initially A-rich region (21.5-9)
r
=
1
for (a) the entering B-rich stream, or
(b)
initially B-rich region (21.5-10)
It follows that, for equal diffusivities, the time-smoothed concentration profiles,
-
T(x,
y,
z, t) are identical for both solutes, where
However, the fluctuating quantities
r'
are also of interest, as they are measures of "un-
mixedness." These can be equal only in a statistical sense. To show this, we subtract
Eq.
21.5-11 from Eq. 21.5-7, and then square the result and time-smooth it to give
Here
d(x,
y,
z, t) is a dimensionless decay function, which decreases toward zero at large
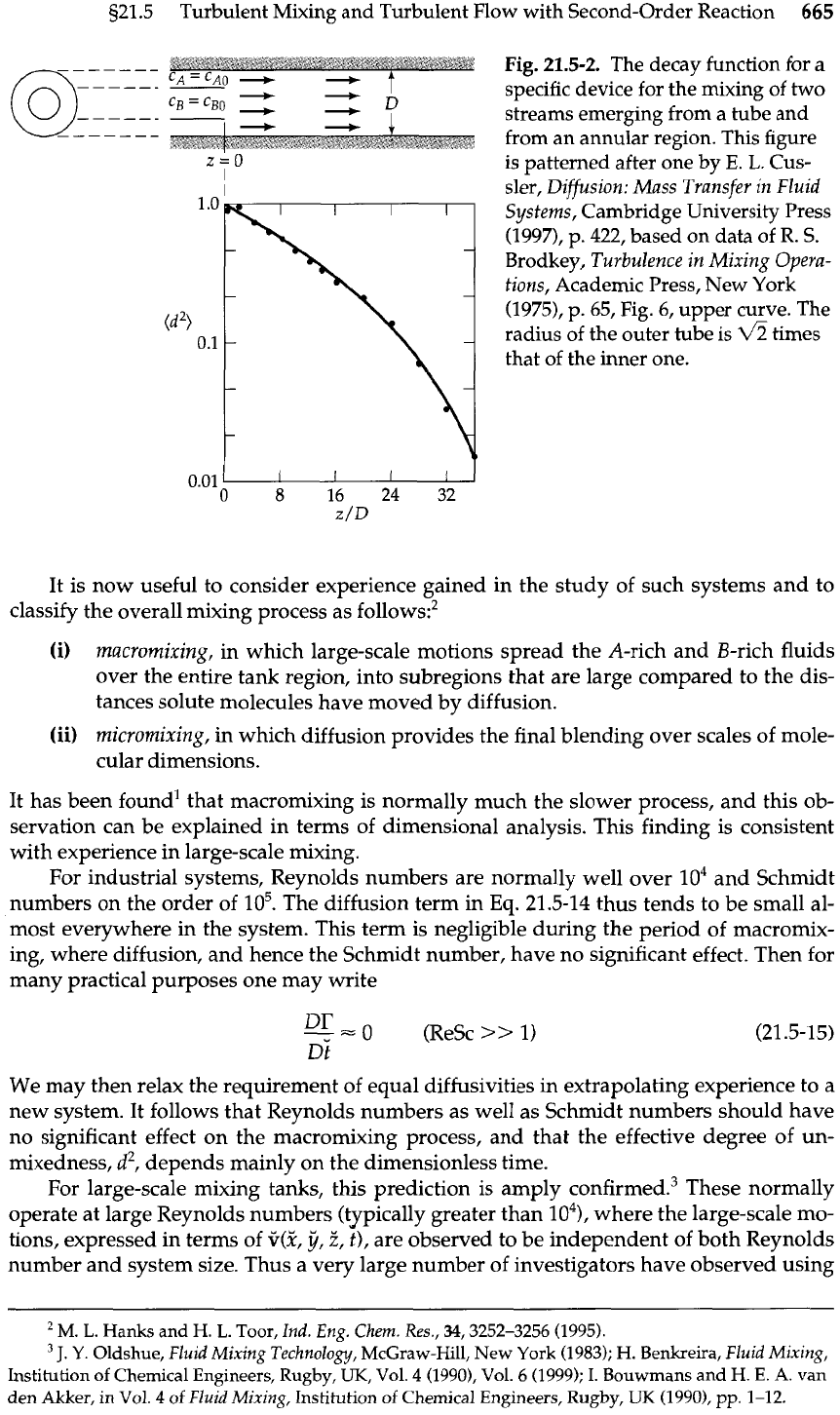
z
[for the motionless mixer in Fig. 21.5-l(a)I, or at large t [for the mixing tank of Fig. 21.5-
I@)]. Cross-sectional averages of this quantity can be measured, and are shown in Fig.
21.5-2.
It remains to determine the functional dependence of the decay function, and to do
this we introduce the dimensionless variables:
Then
Eq.
21.5-8 becomes
Dr
-
1
+zr
D
ReSc
in which Re
=
I,u,p/p.
In order to be able to draw specific conclusions, we now focus our attention on mix-
ing tanks [see Fig. 21.5(b)], and further assume low-viscosity liquids and low-molecular-
weight solutes. For these systems
1,
is normally chosen to be the diameter of the
impeller, and
v,
to be
I&,
where
N
is the rate of impeller rotation in revolutions per unit
time.
1
B+
Fig.
21.5-1.
Two types
of
mixers:
(a)
a baffled
(a)
mixer with no moving
parts;
(b)
a
batch mixer
(b)
with a stirrer.
521.5
Turbulent Mixing and Turbulent Flow with Second-Order Reaction
665
Fig.
21.5-2.
The decay function for a
specific device for the mixing of two
streams emerging from a tube and
from an annular region. This figure
is patterned after one by
E. L.
Cus-
sler, Diffusion: Mass Transfer
in
Fluid
Systems, Cambridge University Press
(1997),
p.
422,
based on data of
R.
S.
Brodkey, Turbulence in Mixing Opera-
tions, Academic Press, New York
(1975),
p.
65,
Fig.
6,
upper curve. The
radius of the outer tube is
fi
times
that of the inner one.
It is now useful to consider experience gained in the study of such systems and to
classify the overall mixing process as
follow^:^
(i)
macromixing, in which large-scale motions spread the A-rich and B-rich fluids
over the entire tank region, into subregions that are large compared to the dis-
tances solute molecules have moved by diffusion.
(ii)
micromixing,
in
which diffusion provides the final blending over scales of mole-
cular dimensions.
It has been found1 that macromixing is normally much the slower process, and this ob-
servation can be explained in terms of dimensional analysis. This finding is consistent
with experience in large-scale mixing.
For industrial systems, Reynolds numbers are normally well over
lo4
and Schmidt
numbers on the order of lo5. The diffusion term in
Eq.
21.5-14 thus tends to be small al-
most everywhere in the system. This term is negligible during the period of macromix-
ing, where diffusion, and hence the Schmidt number, have no significant effect. Then for
many practical purposes one may write
We may then relax the requirement of equal diffusivities in extrapolating experience to a
new system. It follows that Reynolds numbers as well as Schmidt numbers should have
no significant effect on the macromixing process, and that the effective degree of un-
mixedness, d2, depends mainly on the dimensionless time.
For large-scale mixing tanks, this prediction is amply ~onfirmed.~ These normally
operate at large Reynolds numbers (typically greater than
lo4),
where the large-scale mo-
tions, expressed in terms of
+(?,
jl,
if
t),
are observed to be independent of both Reynolds
number and system size. Thus a very large number of investigators have observed using
M.
L.
Hanks and
H.
L.
Toor,
Ind.
Eng.
Chem.
Res.,
34,3252-3256 (1995).
J.
Y.
Oldshue,
Fluid Mixing
Technology,
McGraw-Hill, New York (1983);
H.
Benkreira,
Fluid Mixing,
Institution of Chemical Engineers,
Rugby,
UK,
Vol.
4
(1990), Vol. 6 (1999); I. Bouwmans and
H.
E.
A.
van
den Akker, in Vol.
4
of
Fluid Mixing,
Institution of Chemical Engineers, Rugby,
UK
(1990),
pp.
1-12.

666
Chapter
21
Concentration Distributions in Turbulent Flow
many different mixer geometries, that the product of the required mixing time
t,,
and
rotation rate N is a constant independent of mixer size and Reynolds number:
That is, the required mixing time
t,,
corresponds, for a given tank geometry, essen-
tially to the required number of turns of the impeller. This expectation is confirmed by
experience.
This finding is consistent with observations2 that both the dimensionless volume
flow rate through the impeller, Q/ND~, and the tank friction factor, plpIV3D5, are con-
stants, depending only on the tank and impeller geometries (see Problem
6C.3).
Here
Q
is the volumetric flow in the jet produced by the impeller, and
P
is the power required to
turn it.
Similar remarks usually apply to motionless mixers, where increasing the flow ve-
locities typically has little effect on the degree of mixing. However, approximations like
this must be tested, and such tests should be considered as first steps in an experimental
program. As a practical matter, these approximations are almost always reliable on
scale-up, since Reynolds numbers normally increase with equipment size.
Reaction Occurring
We next consider the effects of a homogeneous, irreversible chemical reaction, and for
simplicity we write this as
A
+
B
4
products. Again we assume dilute solutions, so that
the heat of reaction and the presence of reaction products have no significant effect.
In
addition, we assume equal diffusivities for the two solutes.
We next define
Then when we subtract Eq. 21.5-2 from Eq. 21.5-1, we find that the description of
~,e,cti,,
is identical to that for its nonreactive counterpart. Hence
By subtracting from this its time-smoothed counterpart, we find that an equation like
Eq.
21.5-18 must hold for the fluctuations:
(4-4)
=(")
CAO
+
CBO
reactive nonreactive
The time-smoothed mean square of the quantity on the right side is equal to
d2,
which
is
measurable as illustrated in Fig. 21.5-2, and therefore we have a way of predicting the
corresponding quantity for reacting systems.
Equation 21.5-19 suggests that the fluctuations in
cA
and
cB
in reactive problems
occur on the same time and distance scales as for nonreactive problems. Note that this is
true for arbitrary geometry, flow conditions, and reaction kinetics. We are now ready to
consider special cases.
We begin with a fast reaction, for which the two solutes cannot coexist, and the rate
of the reaction is controlled by the diffusion of the species toward each other. Then, for
the first (macromixing) stage of the blending process, where diffusion is very slow com-
pared to the larger-scale convective processes, there is no significant reaction. In this,
typically dominant, stage of the blending process
(")
=(")
reactive nonreactive
