Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena

Подождите немного. Документ загружается.

53.7

Dimensional Analysis of the Equations of Change

53.7

DIMENSIONAL ANALYSIS OF THE EQUATIONS

CHANGE

Suppose that we have taken experimental data on, or made photographs of, the flow

through some system that cannot be analyzed by solving the equations of change analyt-

ically. An example of such a system is the flow of a fluid through an orifice meter in a

pipe (this consists of a disk with a centered hole in it, placed in the tube, with a pressure-

sensing device upstream and downstream of the disk). Suppose now that we want to

scale up (or down) the experimental system, in order to build a new one in which exactly

the same flow patterns occur [but appropriately scaled up (or down)]. First of all, we

need to have geometric similarity: that is, the ratios of all dimensions of the pipe and ori-

fice plate in the original system and in the scaled-up (or scaled-down) system must be

the same. In addition, we must have dynamic similarity: that is, the dimensionless groups

(such as the Reynolds number) in the differential equations and boundary conditions

must be the same. The study of dynamic similarity is best understood by writing the

equations of change, along with boundary and initial conditions, in dimensionless

For simplicity we restrict the discussion here to fluids of constant density and vis-

cosity, for which the equations of change are Eqs. 3.1-5 and 3.5-7

p-v

-VY

iLV2v

In most flow systems one can identify the following "scale factors": a characteristic

length I,, a characteristic velocity v,, and a characteristic modified pressure

pgh, (for example, these might be a tube diameter, the average flow velocity, and the

modified pressure at the tube exit). Then we can define dimensionless variables and dif-

ferential operators as follows:

We have suggested two choices for the dimensionless pressure, the first one being con-

venient for high Reynolds numbers and the second for low Reynolds numbers. When

the equations of change in Eqs. 3.7-1 and 3.7-2 are rewritten in terms of the dimension-

less quantities, they become

Birkhoff,

Hydrodynamics,

Dover, New York (1955), Chapter

IV.

Our dimensional analysis

procedure corresponds to Birkhoff's "complete inspectional analysis."

Powell,

Elementary

Text

Hydraulics

and Fluid

Mechanics,

Macmillan, New York (19511,

Chapter

VIII;

and

Rouse and

Ince,

History

Hydraulics,

Dover, New York (1963) have interesting

historical material regarding the dimensionless groups and the persons for whom they were named.

Chapter 3 The Equations of Change for Isothermal Systems

In these dimensionless equations, the four scale factors I,,

v,,

p, and

appear in one dimen-

sionless group. The reciprocal of this group is named after a famous fluid dynamicist3

Reynolds number

ro7n

The magnitude of this dimensionless group gives an indication of the relative impor-

tance of inertial and viscous forces in the fluid system.

From the two forms of the equation of motion given in Eq. 3.7-9, we can gain some

perspective on the special forms of the Navier-Stokes equation given in 53.5. Equation

3.7-9a gives the Euler equation of Eq. 3.5-9 when Re

and Eq. 3.7-913 gives the creep-

ing flow equation of Eq. 3.5-8 when Re

1. The regions of applicability of these and

other asymptotic forms of the equation of motion are considered further in

s54.3

and

4.4.

Additional dimensionless groups may arise in the initial and boundary conditions;

two that appear in problems with fluid-fluid interfaces are

Froude number

n:n

[L]

Weber number

~O~P

The first of these contains the gravitational acceleration

and the second contains the in-

terfacial tension

which may enter into the boundary conditions, as described in Prob-

lem

3C.5.

Still other groups may appear, such as ratios of lengths in the flow system (for

example, the ratio of tube diameter to the diameter of the hole in an orifice meter).

The flow of an incompressible Newtonian fluid past a circular cylinder is to be studied exper-

imentally. We want to know how the flow patterns and pressure distribution depend on the

Transverse Flow

cylinder diameter, length, the approach velocity, and the fluid density and viscosity. Show

around a Circular

how to organize the work so that the number of experiments needed will be minimized.

Cylindefl

SOLUTION

For the analysis we consider an idealized flow system: a cylinder of diameter

and length

submerged in an otherwise unbounded fluid of constant density and viscosity. Initially the

fluid and the cylinder are both at rest. At time

the cylinder is abruptly made to move

with velocity

in the negative x direction. The subsequent fluid motion is analyzed by using

coordinates fixed in the cylinder axis as shown in Fig. 3.7-1.

The differential equations describing the flow are the equation of continuity (Eq. 3.7-1)

and the equation of motion (Eq. 3.7-2).

The

initial condition for

is:

I.C.

ifx2+y2>~D20rifIzI>~~,

v=ij,v,

(3.7-13)

The boundary conditions for

0 and all z are:

B.C. 1

B.C. 2

B.C.

asx2

z2-+

03,

Zixvm

v=O

asx+

-03

aty

Y+Y,

See fn. 1 in

s2.2.

William

Froude (1810-1879) (rhymes with "food") studied at Oxford and worked as a civil

engineer concerned with railways and steamships. The Froude number is sometimes defined as the

square root of the group given in

Eq.

3.7-1 1.

Moritz

Weber

(1871-1951) (pronounced "Vayber") was

professor of naval architecture in Berlin;

another dimensionless group involving the surface tension in the

capillary

number,

defined as Ca

[pvo/u].

This example is adapted from

Feynman,

B. Leighton, and M. Sands,

The

Feynman Lectures

Physics,

Vol.

11,

Addison-Wesley, Reading, Mass.

(19641, s41-4.

53.7

Dimensional Analysis of the Equations of Change

Fluid

approaches

from

-w

with uniform

Fig.

3.7-1.

Transverse flow around a cylinder.

Now we rewrite the problem in terms of variables made dimensionless with the characteristic

length Dl velocity v,, and modified pressure

9,.

The resulting dimensionless equations of

change are

(d.1)

=Of

and

Y+

[+ad+]

-eO

+-V2+

in which Re

Dv,p/p. The corresponding initial and boundary conditions are:

I.C.

B.C.

ij2

+-+

tix

if k2

and

121

~(L/D),

;=o

asf+ -waty= 0, 9+0

If we were bright enough to be able to solve the dimensionless equations of change along with

the dimensionless boundary conditions, the solutions would have to be of the following form:

+(it

ij,

Re,

LID)

and

@(?, ij,i,

Re,

LID)

(3.7-23,24)

That is, the dimensionless velocity and dimensionless modified pressure can depend only

on the dimensionless parameters Re and

D and the dimensionless independent variables

ijf

and

This completes the dimensional analysis of the problem. We have not solved the flow

problem, but have decided on a convenient set of dimensionless variables to restate the prob-

lem and suggest the form

the solution. The analysis shows that if we wish to catalog the

flow patterns for flow past a cylinder, it will suffice to record them (e.g., photographically) for

a series of Reynolds numbers Re

Dv,p/p and

L/D

values; thus, separate investigations

into the roles of

v,,

and

are unnecessary. Such a simplification saves a lot of time

and expense. Similar comments apply to the tabulation of numerical results, in the event that

one decides to make a numerical assault on the pr~blem.~,~

Analytical solutions of this problem at very small Re and infinite

L/D

are reviewed in

Rosenhead (ed.),

Laminar Boundary Layers,

Oxford University Press (1963), Chapter

IV.

An important

feature of this two-dimensional problem is the absence of a "creeping flow" solution. Thus the

Vvl-

term in the equation of motion has to be included, even in the limit as Re

0 (see Problem 3B.9). This is

in sharp contrast to the situation for slow flow around

sphere (see g2.6 and g4.2) and around other

finite, three-dimensional objects.

For computer studies of the flow around a long cylinder, see

Harlow and

From,

Scientific

American,

212,104-110 (19651, and S.

Sherwin and

Kamiadakis,

Comput. Math.,

123,189-229 (1995).

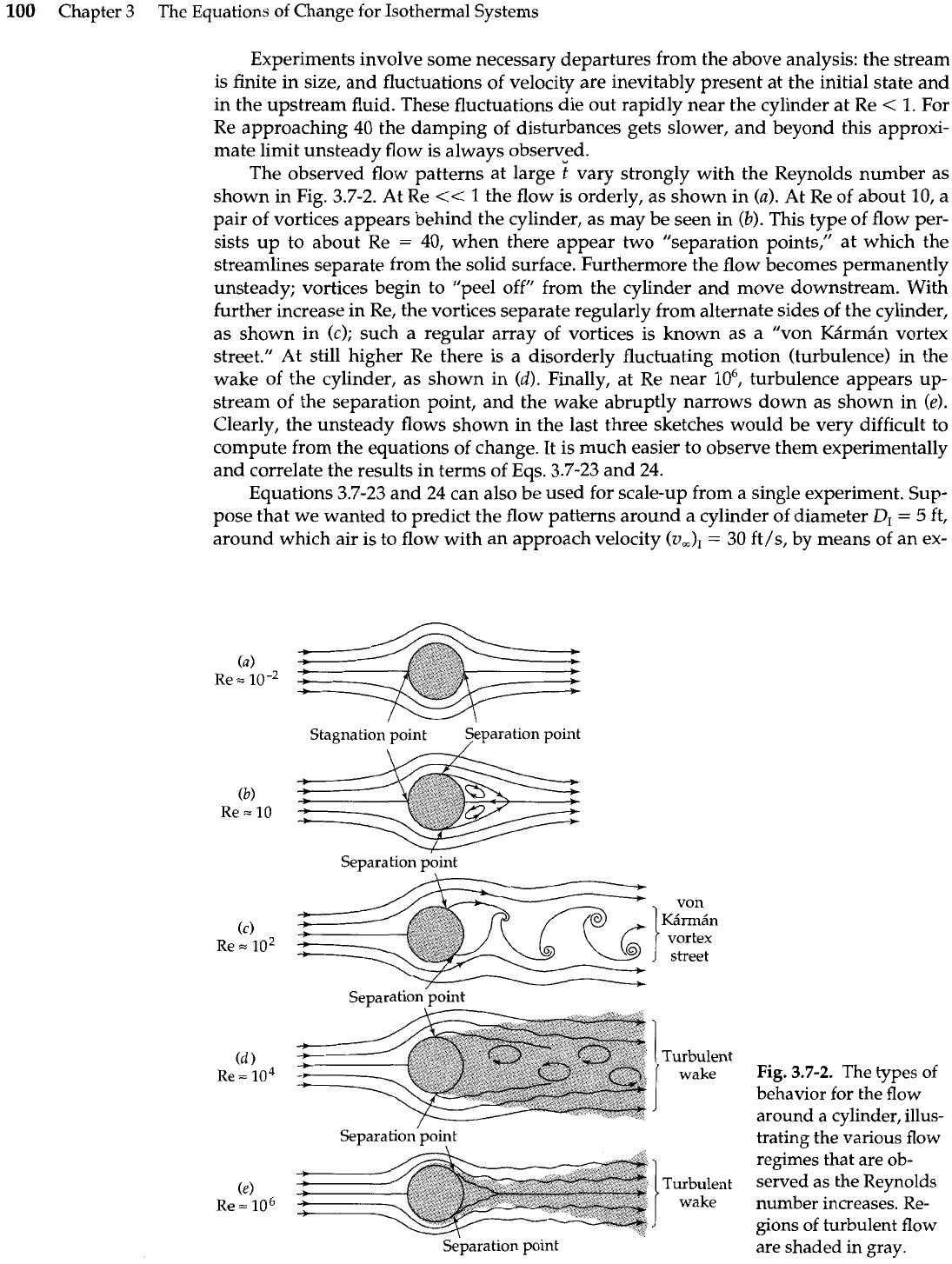
100

Chapter

The Equations of Change for Isothermal Systems

Experiments involve some necessary departures from the above analysis: the stream

is finite in size, and fluctuations of velocity are inevitably present at the initial state and

in the upstream fluid. These fluctuations die out rapidly near the cylinder at Re

For

Re approaching 40 the damping of disturbances gets slower, and beyond this approxi-

mate limit unsteady flow is always observed.

The observed flow patterns at large

vary strongly with the Reynolds number as

shown in Fig. 3.7-2. At Re

the flow is orderly, as shown in

(a).

At Re of about 10, a

pair of vortices appears behind the cylinder, as may be seen in

(b).

This type of flow per-

sists up to about Re

40, when there appear two "separation points," at which the

streamlines separate from the solid surface. Furthermore the flow becomes permanently

unsteady; vortices begin to "peel off" from the cylinder and move downstream. With

further increase in Re, the vortices separate regularly from alternate sides of the cylinder,

as shown in

(c);

such a regular array of vortices is known as a "von KArmtin vortex

street." At still higher Re there is a disorderly fluctuating motion (turbulence) in the

wake of the cylinder, as shown in

(d).

Finally, at Re near

lo6,

turbulence appears up-

stream of the separation point, and the wake abruptly narrows down as shown in

(e).

Clearly, the unsteady flows shown in the last three sketches would be very difficult to

compute from the equations of change. It is much easier to observe them experimentally

and correlate the results in terms of Eqs. 3.7-23 and 24.

Equations 3.7-23 and 24 can also be used for scale-up from a single experiment. Sup-

pose that we wanted to predict the flow patterns around a cylinder of diameter

ft,

around which air is to flow with an approach velocity

(v,),

30 ft/s, by means of an ex-

Stagnation point 7eparation point

Separation point

von

Kbmin

vortex

street

Turbulent

wake

Separation point

Fig.

3.7-2.

The types

behavior for the flow

around a cylinder, illus-

trating the various flow

regimes that are ob-

served as the Reynolds

number increases. Re-

gions of turbulent flow

are shaded in gray.

s3.7

Dimensional Analysis of the Equations of Change

101

periment on a scale model of diameter DII

ft. To have dynamic similarity, we must

choose conditions such that Re,

ReI.

Then if we use the same fluid

the small-scale

experiment as in the large system, so that

p,/fi,

,uI/pI, we find

(v,),,

150

ft/s as the

required air velocity in the small-scale model. With the Reynolds numbers thus equal-

ized, the flow patterns in the model and the full-scale system will look alike: that is, they

are geometrically similar.

Furthermore,

Re is in the range of periodic vortex formation, the dimensionless

time interval

t,v,/D

between vortices will be the same in the two systems. Thus, the vor-

tices will shed

times as fast in the model as in the full-scale system. The regularity of

the vortex shedding at Reynolds numbers from about

lo2

lo4

is utilized commercially

for precise flow metering in large pipelines.

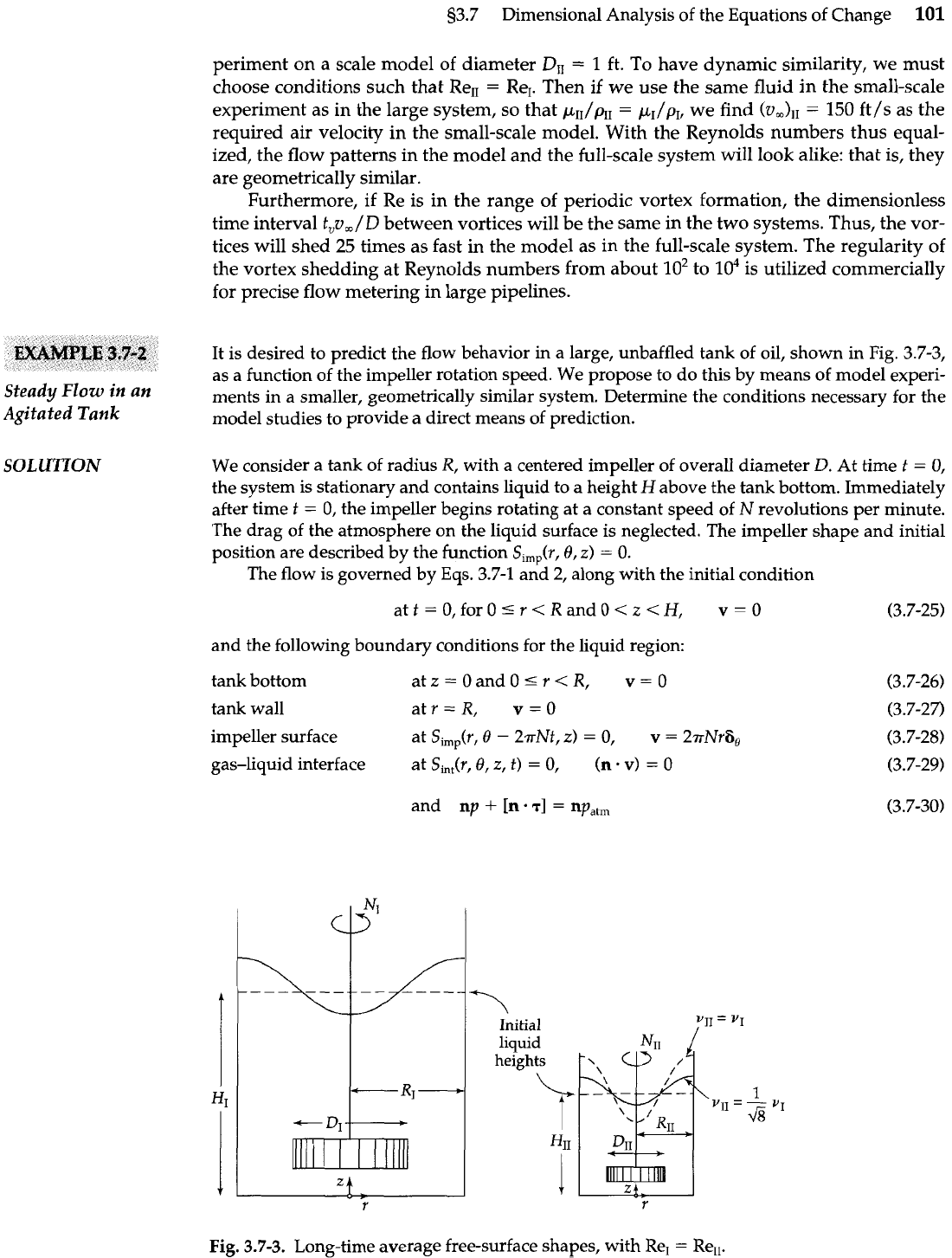
It is desired to predict the flow behavior in a large, unbaffled tank of oil, shown in Fig. 3.7-3,

as a function of the impeller rotation speed. We propose to do this by means of model experi-

Steady

Flow

in an

ments in a smaller, geometrically similar system. Determine the conditions necessary for the

Agitated Tank

model studies to provide a direct means of prediction.

SOLUTION

We consider a tank of radius

with a centered impeller of overall diameter

At time

the system is stationary and contains liquid to a height

above the tank bottom. Immediately

after time

0, the impeller begins rotating at a constant speed of

revolutions per minute.

The drag of the atmosphere on the liquid surface is neglected. The impeller shape and initial

position are described by the function

Si,,(r,

The flow is governed by Eqs. 3.7-1 and 2, along with the initial condition

and the following boundary conditions for the liquid region:

tank bottom atz=OandO~r<R,

v=O

tank wall atr=R,

v=O

impeller surface

at Simp(r,

27~Nt, z)

2n-Nr6,

gas-liquid interface

at Si&, 6, z,

and np

np,,,

Initial

liquid

heights

Fig.

3.7-3.

Long-time average free-surface shapes, with ReI

Rell.

102

Chapter 3 The Equations of Change for Isothermal Systems

Equations 3.7-26 to 28 are the no-slip and impermeability conditions; the surface S,,,(Y,

2~Nf, z)

describes the location of the impeller after Nt rotations. Equation 3.7-29 is the

condition of no mass flow through the gas-liquid interface, described by Sin&,

which has a local unit normal vector

Equation 3.7-30 is a force balance on an element of this

interface (or a statement of the continuity of the normal component of the momentum flux ten-

sor

in which the viscous contributions from the gas side are neglected. This interface is ini-

tially stationary in the plane z

and its motion thereafter is best obtained by measurement,

though it is also predictable in principle by numerical solution of this equation system, which

describes the initial conditions and subsequent acceleration Dv/Dt of every fluid element.

Next we nondimensionalize the equations using the characteristic quantities

ND,

D, and

pa,

along with dimensionless polar coordinates

r/D, 19, and

z/D.

Then the equations of continuity and motion appear as in

Eqs.

3.7-8

and

with Re

D2NpIP.

The initial condition takes the form

and the boundary conditions become:

tank bottom ati=OandO<i<

tank wall

impeller surface

at Simp(?, 6

2~i,

gas-liquid interface

Sint(i,

8,i,

In going from Eq. 3.7-30 to 3.7-36 we have used Newton's law of viscosity in the form of Eq.

1.2-7 (but with the last term omitted, as is appropriate for incompressible liquids). We have

also used the abbreviation

(Vv)+ for the rate-of-deformation tensor, whose dimen-

sionless Cartesian components are

d4/dii)

(ai,/d;Fi).

The quagtities

double brackets are known dimensionless quantities. -The function

simp(;, 8

2rt,

is known for a given impeller design. The unknown function Sin,(<

13,

t) is

measurable photographically, or in principle is computable from the problem statement.

inspection of the dimensionless equations, we find that the velocity and pressure pro-

files must have the form

for a given impeller shape and location. The corresponding locus of the free surface is given by

in which Re

D2NplP and Fr

DN2/g. For time-smoothed observations at large

the depen-

dence on

will disappear, as will the dependence on 6 for this axisymmetric tank geometry.

These results provide the necessary conditions for the proposed model experiment: the

two systems must be

(i)

geometrically similar (same values of R/D and H/D, same impeller

geometry and location), and (ii) operated at the same values of the Reynolds and Froude

numbers. Condition (ii) requires that

s3.7 Dimensional Analysis of the Equations of Change

103

in which the kinematic viscosity

p/p is used. Normally both tanks will operate in the

same gravitational field gl

gII, so that Eq. 3.7-41 requires

Substitution of this into Eq. 3.7-40 gives the requirement

This is an important result-namely, that the smaller tank (11) requires a fluid of smaller kine-

matic viscosity to maintain dynamic similarity. For example, if we use a scale model with

DII

:D,,

then we need to use a fluid with kinematic viscosity

vl,

vI/V%

in the scaled-down

experiment. Evidently the requirements for dynamic similarity are more stringent here than

in the previous example, because of the additional dimensionless group Fr.

In many practical cases, Eq. 3.7-43 calls for unattainably low values of vl,. Exact scale-up

from a single model experiment is then not possible. In some circumstances, however, the ef-

fect of one or more dimensionless groups may be known to be small, or may be predictable

from experience with similar systems; in such situations, approximate scale-up from a single

experiment is still fea~ible.~

This example shows the importance of including the boundary conditions in a dimen-

sional analysis. Here the Froude number appeared only in the free-surface boundary condi-

tion

Eq.

3.7-36. Failure to use this condition would result in the omission of the restriction

Eq. 3.7-42, and one might improperly choose

vl,

vl.

If one did this, with Re,,

ReI, the

Froude number in the smaller tank would be too large, and the vortex would be too deep, as

shown by the dotted line in Fig. 3.7-3.

EXAMPLE

3.7-3

Show that the mean axial gradient of the modified pressure

for creeping flow of a fluid of

constant p and

through a tube of radius

uniformly packed for a length

with

Pressure Drop for

solid particles of characteristic size D,

Creeping Flow

Packed Tube

A@')

P(%)

K(geom) (3.7-44)

Here

(-.

denotes an average over a tube cross section within the packed length

and the

function K(geom) is a constant for a given bed geometry (i.e., a given shape and arrangement

of the particles).

SOLUTION

We choose D, as the characteristic length and (v,) as the characteristic velocity. Then the i~ter-

stitial fluid motion is determined by Eqs. 3.7-8 and 3.7-913, with

;

v/(v,)

and

90)Dp/p(v,), along with no-slip conditions on the solid syrfaces and the modified pres-

sure difference A(9)

(9,)

(9,).

The solutions for

;

and

in creeping flow (D,(v,)p/p

accordingly depend only on

and

for a given particle arrangement and shape. Then

the mean axial gradient

depends only on the bed-geometry as long as

and

are large relative to D,. Inserting the

foregoing expression for

we immediately obtain Eq. 3.7-44.

For

introduction to methods for scale-up with incomplete dynamic similarity, see

Powell,

An Elementary

Text

in Hydraulics and Fluid Mechanics,

Macmillan, New York

(1951).

104

Chapter 3 The Equations of Change for Isothermal Systems

PROBLEMS

QUESTIONS FOR DISCUSSION

What is the physical meaning of the term

Ay(pv,)l,

in Eq. 3.1-2? What is the physical mean-

ing of (V

v)? of

pv)?

By making a mass balance over

volume element (Ar)(rAO)(Az) derive the equation of conti-

nuity in cylindrical coordinates.

What is the physical meaning of the term Ax Ay(pv,v,)l, in Eq. 3.2-2? What is the physical

meaning of [V

pwl?

What happens when

is set equal to unity in

Eq.

3.5-4?

Equation

in Table 3.5-1 is

not

restricted to fluids with constant density, even though p is to

the left of the substantial derivative. Explain.

In the tangential annular flow problem in Example 3.5-3, would you expect the velocity pro-

files relative to the inner cylinder to be the same in the following two situations: (i) the inner

cylinder is fixed and the outer cylinder rotates with an angular velocity

fl;

(ii) the outer cylin-

der is fixed and the inner cylinder rotates with an angular velocity

-a?

Both flows are pre-

sumed to be laminar and stable.

Suppose that, in Example 3.6-4, there were two immiscible liquids in the rotating beaker.

What would be the shape of the interface between the two liquid regions?

Would the system discussed in Example 3.6-5 be useful as a viscometer?

In Eq. 3.6-55, explain by means of a carefully drawn sketch the choice of limits in the integra-

tion and the meaning of each factor in the first integrand.

What factors would need to be taken into account in designing a mixing tank for use on the

moon by using data from a similar tank on earth?

3A.1

Torque required to turn a friction bearing (Fig.

3A.1). Calculate the required torque in lbf

ft and power

consumption in horsepower to turn the shaft in the friction

bearing shown in the figure. The length of the bearing sur-

face on the shaft is 2 in, and the shaft is rotating at 200

rpm. The viscosity of the lubricant is 200 cp, and its den-

sity is

lb,/ft3. Neglect the effect of eccentricity.

Answers:

0.32 lbf. ft; 0.012 hp

0.009 kW

Fig.

3A.1.

Friction

bearing.

3A.2

Friction loss in bearings? Each of two screws on a

large motor-ship is driven by a 4000-hp engine. The shaft

that connects the motor and the screw is 16 in. in diameter

This problem

was

contributed by Prof.

Crosby,

University

Wisconsin.

and rests in a series of sleeve bearings that give a 0.005 in.

clearance. The shaft rotates at 50 rpm, the lubricant has a

viscosity of 5000 cp, and there are 20 bearings, each

length. Estimate the fraction of engine power expended in

rotating the shafts in their bearings. Neglect the effect of

the eccentricity.

Answer:

0.1 15

3A.3

Effect of altitude on air pressure. When standing

at the mouth of the Ontonagon River on the south shore of

Lake Superior (602 ft above mean sea level), your portable

barometer indicates a pressure of 750 mm Hg. Use the

equation of motion to estimate the barometric pressure at

the top of Government Peak (2023 ft above mean sea level)

in the nearby Porcupine Mountains. Assume that the tem-

perature at lake Level is 70°F and that the temperature de-

creases with increasing altitude at a steady rate of 3°F per

1000 feet. The gravitational acceleration at the south shore

of Lake Superior is about 32.19 ft/s2, and its variation with

altitude may be neglected in this problem.

Answer:

713 mm Hg

9.49

lo4

N/m2

3A.4

Viscosity determination with a rotating-cylinder

viscometer. It is desired to measure the viscosities of su-

crose solutions of about 60% concentration by weight at

about

20°C

with a rotating-cylinder viscometer such as

that shown in Fig. 3.5-1. This instrument has an inner

cylinder 4.000 cm in diameter surrounded by a rotating

Problems

105

concentric cylinder 4.500 cm in diameter. The length

4.00 cm. The viscosity of a 60% sucrose solution at 20°C is

about 57

cp,

and its density is about 1.29 g/cm3.

On the basis of past experience it seems possible that

end effects will be important, and it is therefore decided to

calibrate the viscometer by measurements on some known

solutions of approximately the same viscosity as those of

the unknown sucrose solutions.

Determine a reasonable value for the applied torque

to be used in calibration

the torque measurements are re-

liable within 100 dyne/cm and the angular velocity can be

measured within 0.5%. What will be the resultant angular

velocity?

3A.5

Fabrication

a parabolic mirror. It is proposed to

make a backing for a parabolic mirror, by rotating a pan of

slow-hardening plastic resin at constant speed until it

hardens. Calculate the rotational speed required to pro-

duce a mirror of focal length

100 cm. The focal length is

one-half the radius of curvature at the axis, which in turn

given by

Answer:

21 .I rpm

3A.6

Scale-up of an agitated tank. Experiments with a

small-scale agitated tank are to be used to design a geo-

metrically similar installation with linear dimensions 10

times as large. The fluid in the large tank will be a heavy

oil

with

13.5 cp and

0.9 g/cm3. The large tank is to

have an impeller speed of 120 rpm.

(a)

Determine the impeller speed for the small-scale

model, in accordance with the criteria for scale-up given in

Example 3.7-2.

(b)

Determine the operating temperature for the model if

water is to be used as the stirred fluid.

Answers:

(a) 380 rpm, (b)

60°C

3A.7

Air entrainment in a draining tank (Fig.

3A.7).

molasses storage tank 60 ft in diameter is to be built with a

draw-off line

ft in diameter,

ft from the sidewall of the

Fig.

3A.7.

Draining of a molasses tank.

tank and extending vertically upward

ft from the tank

bottom. It is known from experience that, as molasses is

withdrawn from the tank, a vortex will form, and, as the

liquid level drops, this vortex will ultimately reach the

draw-off pipe, allowing air to be sucked into the molasses.

This is to be avoided.

It is proposed to predict the minimum liquid level at

which this entrainment can be avoided, at a draw-off rate

of 800 gal/min, by a model study using a smaller tank. For

convenience, water at 68OF is to be used for the fluid in the

model study.

Determine the proper tank dimensions and operating

conditions for the model if the density of the molasses is

1.286 g/cm3 and its viscosity is 56.7 cp. It may be assumed

that, in either the full-size tank or the model, the vortex

shape is dependent only on the amount of the liquid in the

tank and the draw-off rate; that is, the vortex establishes it-

self very rapidly.

38.1

Flow between coaxial cylinders and concentric

spheres.

(a) The space between two coaxial cylinders is filled with

an incompressible fluid at constant temperature. The radii

of the inner and outer wetted surfaces are

and

re-

spectively. The angular velocities of rotation of the inner

and outer cylinders are

and

a,.

Determine the velocity

distribution

the fluid and the torques on the two cylin-

ders needed to maintain the motion.

(b) Repeat part

(a)

for two concentric spheres.

Answers:

(a)

3B.2

Laminar flow in a triangular duct (Fig. 3B.2h2

One type of compact heat exchanger is shown in Fig.

3B.2(a). In order to analyze the performance of such an

apparatus, it is necessary to understand the flow in a duct

whose cross section is an equilateral triangle. This is done

most easily by installing a coordinate system as shown in

Fig. 3B.2(b).

(a) Verify that the velocity distribution for the laminar

flow of a Newtonian fluid in a duct of this type is given

An alternative formulation of

the

velocity profile is given

Landau and

Lifshitz,

Fluid

Mechanics,

Pergamon,

Oxford,

2nd

edition

(19871,

54.

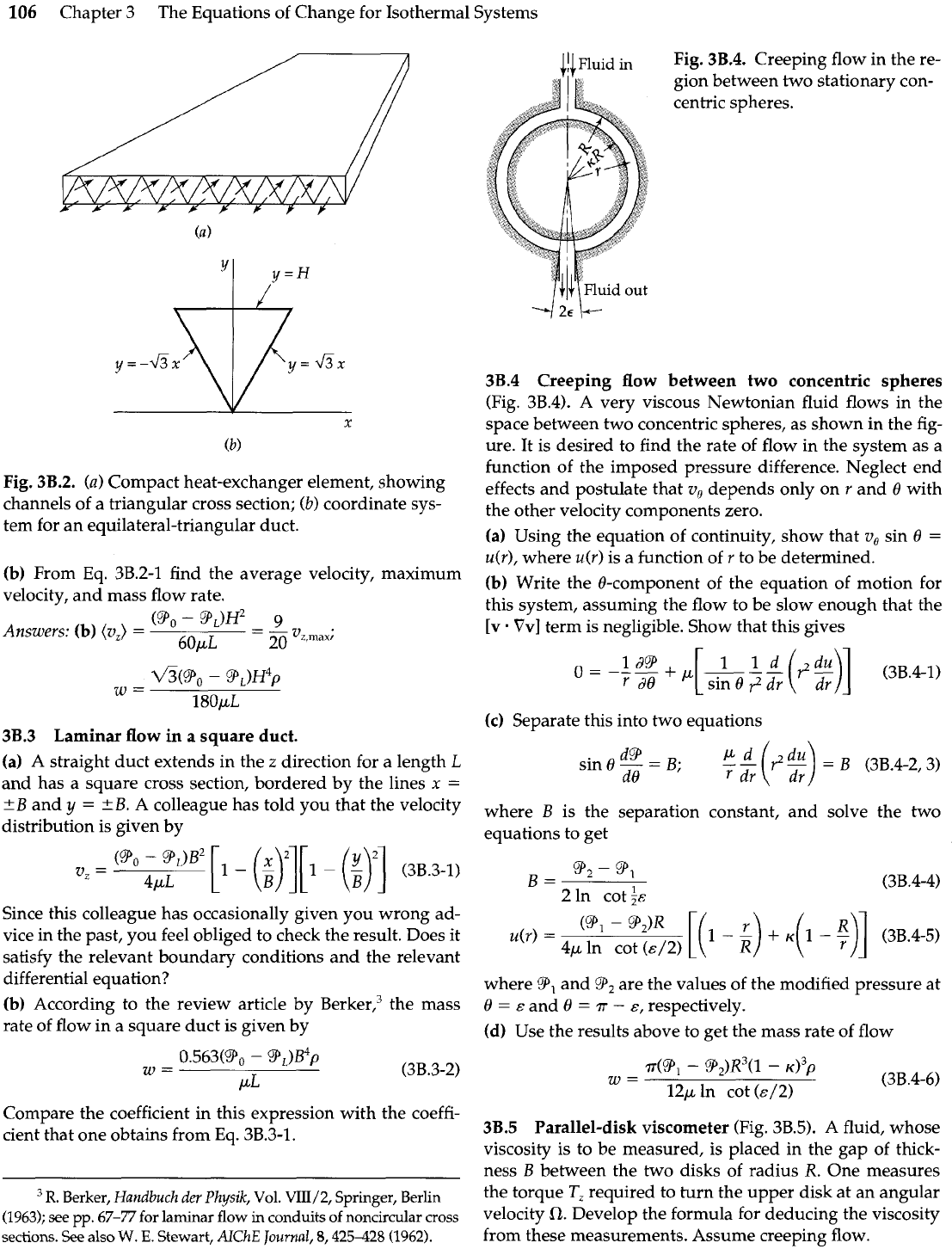
106

Chapter 3 The Equations of Change for Isothermal Systems

Fig.

3B.2.

(a)

Compact heat-exchanger element, showing

channels of a triangular cross section;

(b)

coordinate sys-

tem for an equilateral-triangular duct.

(b) From Eq. 3B.2-1 find the average velocity, maximum

velocity, and mass flow rate.

3B.3

Laminar flow in

square duct.

(a)

straight duct extends in the

direction for a length

and has a square cross section, bordered

the lines

and

?B.

colleague has told you that the velocity

distribution is given by

"'"

[[I

($)i][l

(:)I

(38.34)

Since this colleague has occasionally given you wrong ad-

vice in the past, you feel obliged to check the result. Does it

satisfy the relevant boundary conditions and the relevant

differential equation?

(b) According to the review article by BerkerI3 the mass

rate of flow in a square duct is given by

Compare the coefficient in this expression with the coeffi-

cient that one obtains from Eq. 3B.3-1.

Berker,

Handbuch der Physik,

Vol.

VIII/2,

Springer, Berlin

(1963);

see

pp.

67-77

for laminar flow

conduits of noncirmlar cross

sections.

See

also

Stewart,

AlChE

Journal,

8,425428

(1962).

Fig.

3B.4.

Creeping flow in the re-

gion between two stationary con-

centric spheres.

3B.4

Creeping flow between two concentric spheres

(Fig. 3B.4).

very viscous Newtonian fluid flows in the

space between two concentric spheres, as shown in the fig-

ure. It is desired to find the rate of flow in the system as a

function of the imposed pressure difference. Neglect end

effects and postulate that

depends only on r and

with

the other velocity components zero.

(a)

Using the equation of continuity, show that

sin

~(r), where u(r) is a function of

to be determined.

(b) Write the Bcomponent of the equation of motion for

this system, assuming the flow to be slow enough that the

VV]

term is negligible. Show that this gives

(c)

Separate this into two equations

sin

(3B.4-2,3)

dtl

where

is the separation constant, and solve the two

equations to get

2 1n cot

u(r)

"')'

[(I

+)]

(384-5)

4p ln cot (s/2)

where

and

are the values of the modified pressure at

and

.rr

respectively.

(d)

Use the results above to get the mass rate of flow

g(P1

g2)R3(1

K)~~

(3B.4-6)

12p

cot

(c?/2)

3B.5

Parallel-disk viscometer

(Fig.

3B.5). A fluid, whose

viscosity is to be measured, is placed in the gap of thick-

ness

between the two disks of radius

One measures

the torque

required to turn the upper disk at an angular

velocity

cC1.

Develop the formula for deducing the viscosity

from these measurements. Assume creeping flow.