Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena

Подождите немного. Документ загружается.

Problems

(a)

Write down the expression for R as a function of

(b)

Change the independent variable in the above equation to R, so that the equation becomes

(c)

Integrate the equation, and then show that the solution can be rearranged to give

Interpret the result. The approximation used here that a flow between nonparallel surfaces

can be regarded locally as flow between parallel surfaces is sometimes referred to as the lubri-

cation approximation and is widely used in the theory of lubrication. By making a careful

order-of-magnitude analysis, it can be shown that, for this problem, the lubrication approxi-

mation is valid as long as4

2B.11

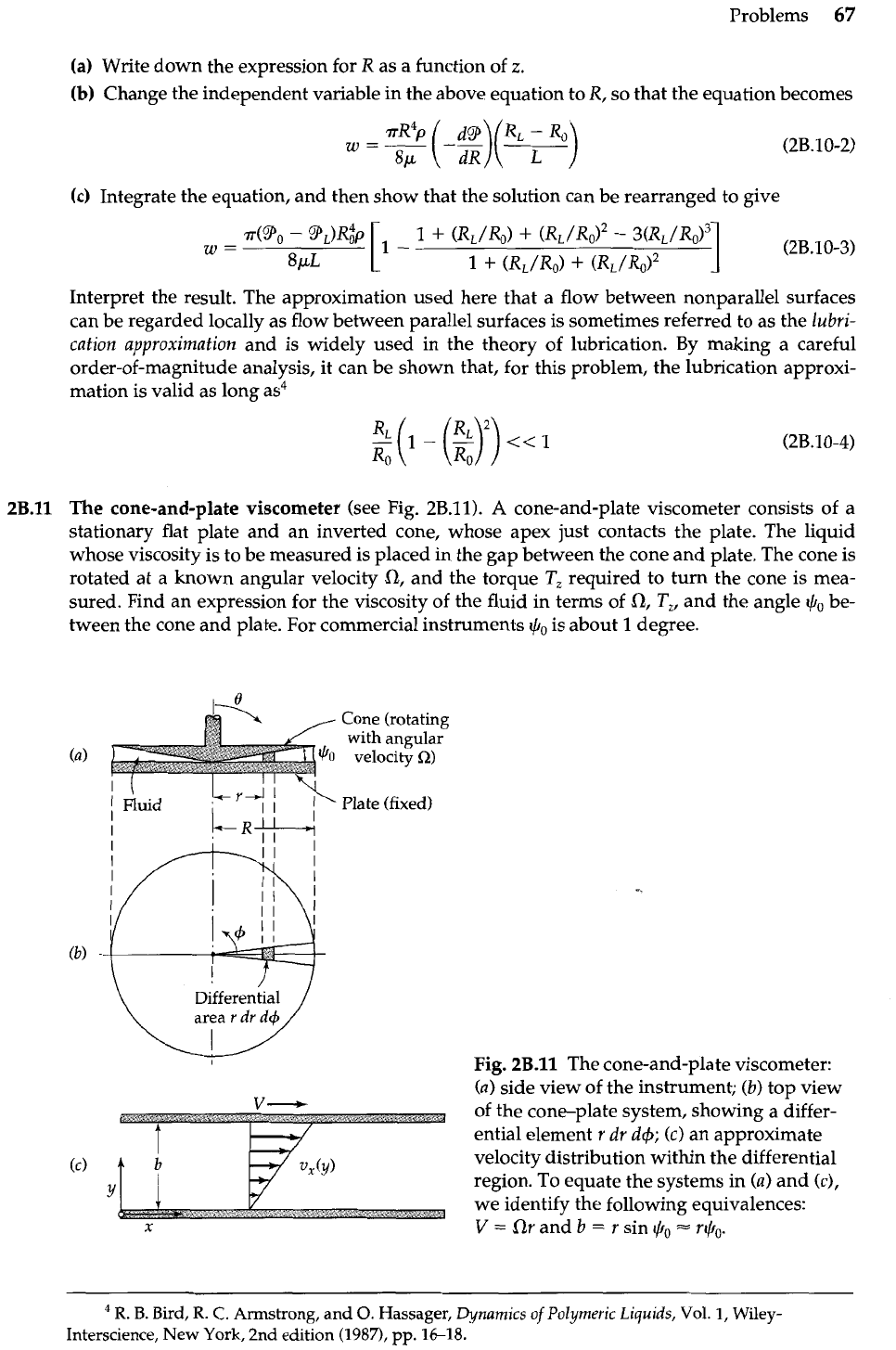
The cone-and-plate viscometer (see Fig. 2B.11).

cone-and-plate viscometer consists of a

stationary flat plate and an inverted cone, whose apex just contacts the plate. The liquid

whose viscosity is to be measured is placed in the gap between the cone and plate. The cone is

rotated at a known angular velocity

and the torque

required to turn the cone is mea-

sured. Find an expression for the viscosity of the fluid in terms of

T,,

and the angle

be-

tween the cone and plate. For commercial instruments

is about

degree.

~ifferential

,,/

area

r dr

Fig.

2B.11

The cone-and-plate viscometer:

(a) side view of the instrument;

(b)

top view

of the cone-plate system, showing a differ-

ential element r dr d+;

(c)

an approximate

(c)

velocity distribution within the differential

region. To equate the systems in (a) and

(c),

we identify the following equivalences:

Or and

sin

i/io

ri/io.

Bird,

Armstrong, and

Hassager,

Dynamics

Polymeric Liquids,

Vol.

Wiley-

Interscience, New

York,

2nd edition (19871,

pp.

16-18.

Chapter 2

Shell Momentum Balances and Velocity Distributions in Laminar Flow

(a)

Assume that locally the velocity distribution in the gap can be very closely approximated

by that for flow between parallel plates, the upper one moving with a constant speed. Verify

that this leads to the

approximate

velocity distribution (in spherical coordinates)

This approximation should be rather good, because

I++,

is so small.

(b)

From the velocity distribution in Eq. 28.11-1 and Appendix B.l, show that a reasonable

expression for the shear stress is

This result shows that the shear stress is uniform throughout the gap. It is this fact that makes

the cone-and-plate viscometer quite attractive. The instrument is widely used, particularly in

the polymer industry.

(c)

Show that the torque required to turn the cone is given by

This is the standard formula for calculating the viscosity from measurements of the torque

and angular velocity for a cone-plate assembly with known

and

rCr,.

(d)

For a cone-and-plate instrument with radius 10 cm and angle

equal to 0.5 degree, what

torque

(in

dyn

cm) is required to turn the cone at an angular velocity of 10 radians per

minute

the fluid viscosity is 100 cp?

Answer:

(d)

40,000 dyn

2B.12

Flow of a fluid in a network of tubes

(Fig. 2B.12). A fluid is flowing in laminar flow from

through a network of tubes, as depicted in the figure. Obtain an expression for the mass

flow rate

of the fluid entering at

(or leaving at

as a function of the modified pressure

drop

9,. Neglect the disturbances at the various tube junctions.

3?7(pA

9B)R4p

Answer: w

20pL

Fluid in

Fluid out

All tubes have the same

radius

and same length

Fig.

2B.12

Flow of a fluid in a network with

branching.

2C.1

Performance of an electric dust collector

(see Fig. 2C.U5.

(a)

dust precipitator consists of a pair of oppositely charged plates between which dust-

laden gases flow. It is desired to establish a criterion for the minimum length of the precipita-

tor in terms of the charge on the particle

the electric field strength

the pressure difference

The answer given in the first edition

this book was incorrect, as pointed out to us in

1970

Nau Gab Lee

Seoul National University.

Problems

Parabolic

velocity

trajectory

distribution

B-:,.''

;

..;,

,.-'

*-:.

",'.

,*-.',~'-(

Pressure

Fig.

2C.1

Particle trajectory in an electric dust collector. The particle that begins at

0 and

ends at

may not necessarily travel the longest distance in the

direction.

(po

pJ,

the particle mass m, and the gas viscosity

That is, for what length

will the smallest

particle present (mass m) reach the bottom just before it has a chance to be swept out of the chan-

nel? Assume that the flow between the plates is laminar so that the velocity distribution is de-

scribed

Eq.

2B.3-2. Assume also that the particle velocity in the

direction is the same as the

fluid velocity

the

direction. Assume further that the Stokes drag on the sphere as well as the

gravity force acting on the sphere as it is accelerated in the negative

direction can be neglected.

(b) Rework the problem neglecting acceleration in the

direction, but including the Stokes drag.

(c)

Compare the usefulness of the solutions in (a) and

(b),

considering that stable aerosol par-

ticles have effective diameters of about 1-10 microns and densities of about

g/cm3.

Answer: (a)

Lmi,

[12(po

pL)2~5m/25p2eCe11'4

2C.2

Residence time distribution in tube flow. Define the residence time function

F(t)

to be that

fraction of the fluid flowing in a conduit which flows completely through the conduit in

time interval t. Also define the mean residence time t, by the relation

(a) An incompressible Newtonian liquid is flowing in a circular tube of length

and radius

and the average flow velocity is (v,). Show that

F(t)

for t

(L/2(vZ))

F(t)

(L/2(~,)t)~

fort

(L/2(vZ))

(b) Show that t,

(L/(v,)).

2C.3

Velocity distribution in a tube. You have received a manuscript to referee for a technical

journal. The paper deals with heat transfer in tube flow. The authors state that, because they

are concerned with nonisothermal flow, they must have a "general" expression for the veloc-

ity distribution, one that can be used even when the viscosity of the fluid is a function of tem-

perature (and hence position). The authors state that a "general expression for the velocity

distribution for flow in a tube" is

in which

r/R. The authors give no derivation, nor do they give a literature citation. As the

referee you feel obliged to derive the formula and list any restrictions implied.

Chapter 2

Shell Momentum Balances and Velocity Distributions in Laminar Flow

2C.4

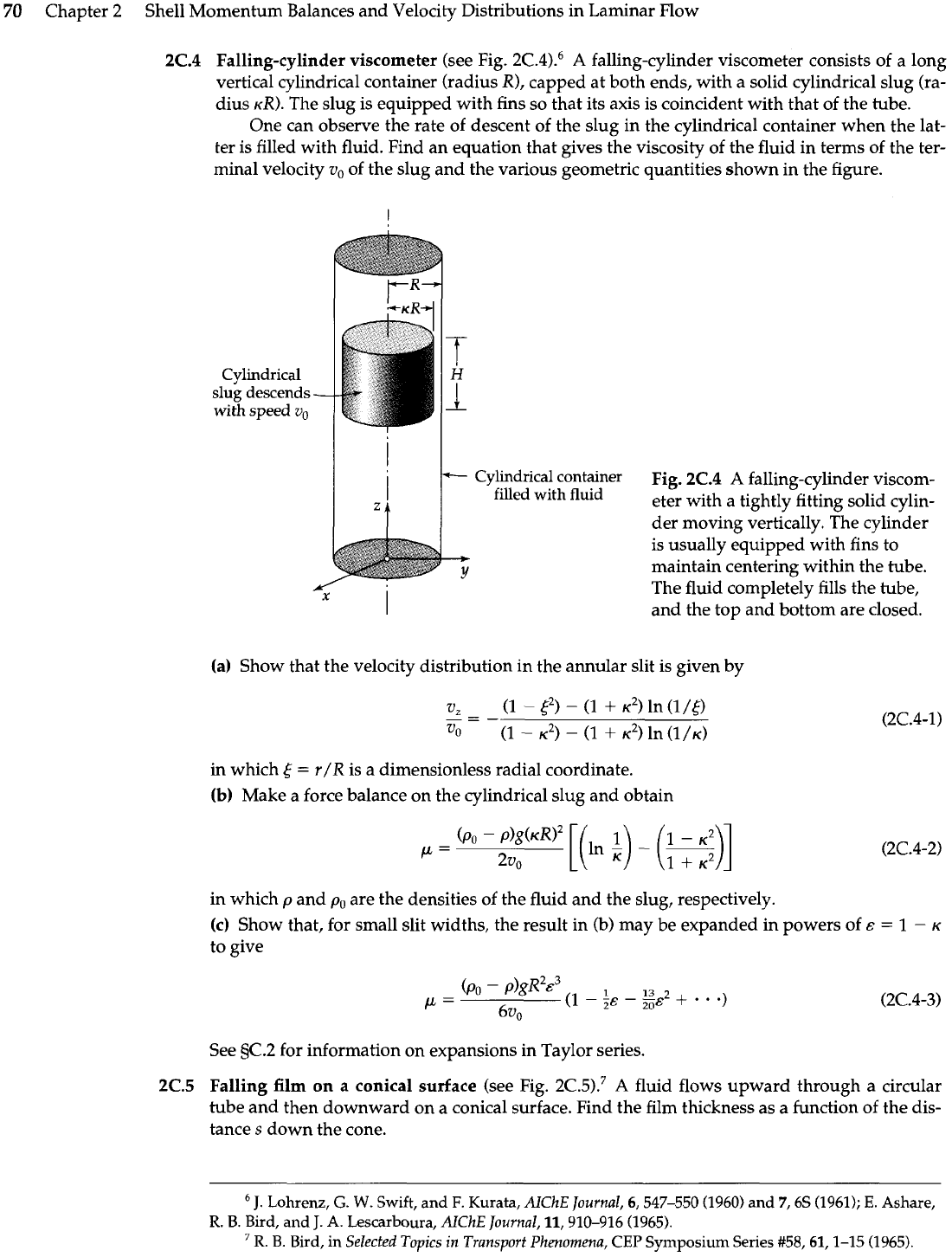
Falling-cylinder viscometer (see Fig. 2C.4).6

falling-cylinder viscometer consists of a long

vertical cylindrical container (radius R), capped at both ends, with a solid cylindrical slug (ra-

dius

KR).

The slug is equipped with fins so that its axis is coincident with that of the tube.

One can observe the rate of descent of the slug in the cylindrical container when the lat-

ter is filled with fluid. Find an equation that gives the viscosity of the fluid in terms of the ter-

minal velocity

of the slug and the various geometric quantities shown in the figure.

Cylindrical

slug descends

with speed

Cylindrical container

Fig.

2C.4

falling-cylinder viscom-

with

fluid

eter with a tightly fitting solid cylin-

der moving vertically. The cylinder

is usually equipped with fins to

----t

maintain centering within the tube.

The fluid completely fills the tube,

and the top and bottom are closed.

(a) Show that the velocity distribution in the annular slit is given

in which

r/R is a dimensionless radial coordinate.

(b)

Make a force balance on the cylindrical slug and obtain

in which

and

are the densities of the fluid and the slug, respectively.

(c)

Show that, for small slit widths, the result in (b) may be expanded in powers of

to give

See sC.2 for information on expansions

Taylor series.

2C.5

Falling film on a conical surface (see Fig. 2C.5).7

fluid flows upward through a circular

tube and then downward on a conical surface. Find the film thickness as a function of the dis-

tance s down the cone.

Lohrenz,

Swift, and

Kurata,

AIChE Journal,

6,547-550 (1960) and 7,6S (1961);

Ashare,

B. Bird, and

A. Lescarboura,

AIChE

Journal,

11,910-916 (1965).

B. Bird, in

Selected Topics in Transport Phenomena,

CEP

Symposium Series #58,61,1-15 (1965).

Problems

downstream distance

sured from the

ilm thickness is

Fluid in with mass

flow rate

Fig. 2C.5

falling film on a conical

surface.

(a)

Assume that the results of 92.2 apply

approximately

over any small region of the cone sur-

face. Show that a mass balance on a ring of liquid contained between

and

gives:

(b)

Integrate this equation and evaluate the constant of integration by equating the mass rate

of flow

up the central tube to that flowing down the conical surface at

Obtain the fol-

lowing expression for the film thickness:

s=d

3pw

(;)

rp2gL

sin 2/3

2C.6

Rotating cone

pump

(see Fig. 2C.6). Find the mass rate of flow through this pump as a func-

tion of the gravitational acceleration, the impressed pressure difference, the angular velocity

of the cone, the fluid viscosity and density, the cone angle, and other geometrical quantities

labeled in the figure.

iredion of flow

Fig. 2C.6 A rotating-cone pump. The variable

with mass rate of

is the distance from the axis of rotation out to

flow

(Ib,

/s)

the center of the slit.

Chapter 2

Shell Momentum Balances and Velocity Distributions in Laminar Flow

(a) Begin by analyzing the system without the rotation of the cone. Assume that it is possible

to apply the results of Problem 2B.3 locally. That is, adapt the solution for the mass flow rate

from that problem by making the following replacements:

replace

(9,

BJ/L

-dP/dz

replace

by 2717

27rz sin

thereby obtaining

B3p

.2.rrz

sin

-=5(-z)

The mass flow rate

is a constant over the range of z. Hence this equation can be integrated

to give

(b)

Next, modify the above result to account for the fact that the cone is rotating with angular

velocity

fl.

The mean centrifugal force per unit volume acting on the fluid in the slit will have

a z-component

approximately

given by

What is the value of

Incorporate this

an additional force tending to drive the fluid

through the channel. Show that this leads to the following expression for the mass rate of flow:

Here

pgLi

cos

2C.7

simple rate-of-climb indicator (see Fig. 2C.7). Under the proper circumstances the simple

apparatus shown in the figure can be used to measure the rate of climb of an airplane. The

gauge pressure inside the Bourdon element is taken as proportional to the rate of climb. For

the purposes of this problem the apparatus may be assumed to have the following properties:

(i) the capillary tube (of radius

and length

with

is of negligible volume but ap-

preciable flow resistance; (ii) the Bourdon element has a constant volume

and offers negli-

gible resistance to flow; and (iii) flow in the capillary

laminar and incompressible, and the

volumetric flow rate depends only on the conditions at the ends of the capillary.

Rate

climb

Capillary-

tube

Bourdon

element

Pressure

outside

inside

Fig.

2C.7

rate-of-climb indicator.

(a)

Develop an expression for the change of air pressure with altitude, neglecting tempera-

ture changes, and considering air to be an ideal gas of constant composition.

(Hint:

Write a

shell balance in which the weight of gas is balanced against the static pressure.)

Problems

(b)

By making a mass balance over the gauge, develop an approximate relation between

gauge pressure p,

p, and rate of climb v, for a long continued constant-rate climb. Neglect

change of air viscosity, and assume changes in air density to be small.

(c)

Develop an approximate expression for the "relaxation time"

trel

of the indicator-that is,

the time required for the gauge pressure to drop to

l/e

of its initial value when the external

pressure is suddenly changed from zero (relative to the interior of the gauge) to some differ-

ent constant value, and maintained indefinitely at this new value.

(d)

Discuss the usefulness of this type of indicator for small aircraft.

(e)

Justify the plus and minus signs in the figure.

Answers:

(a)

dp/dz

-(pM/RT)g

(b)

vZ(8p~/~4)(~g~/~,T), where

R,,

is the gas constant and M is the mole-

cular weight.

(c)

(128/.ir)(pVL/.rrD4@, where

$(p,

p,)

2D.1

Rolling-ball viscometer.

An approximate analysis of the rolling-ball experiment has been

given, in which the results of Problem 28.3 are used.8 Read the original paper and verify the

results.

2D.2

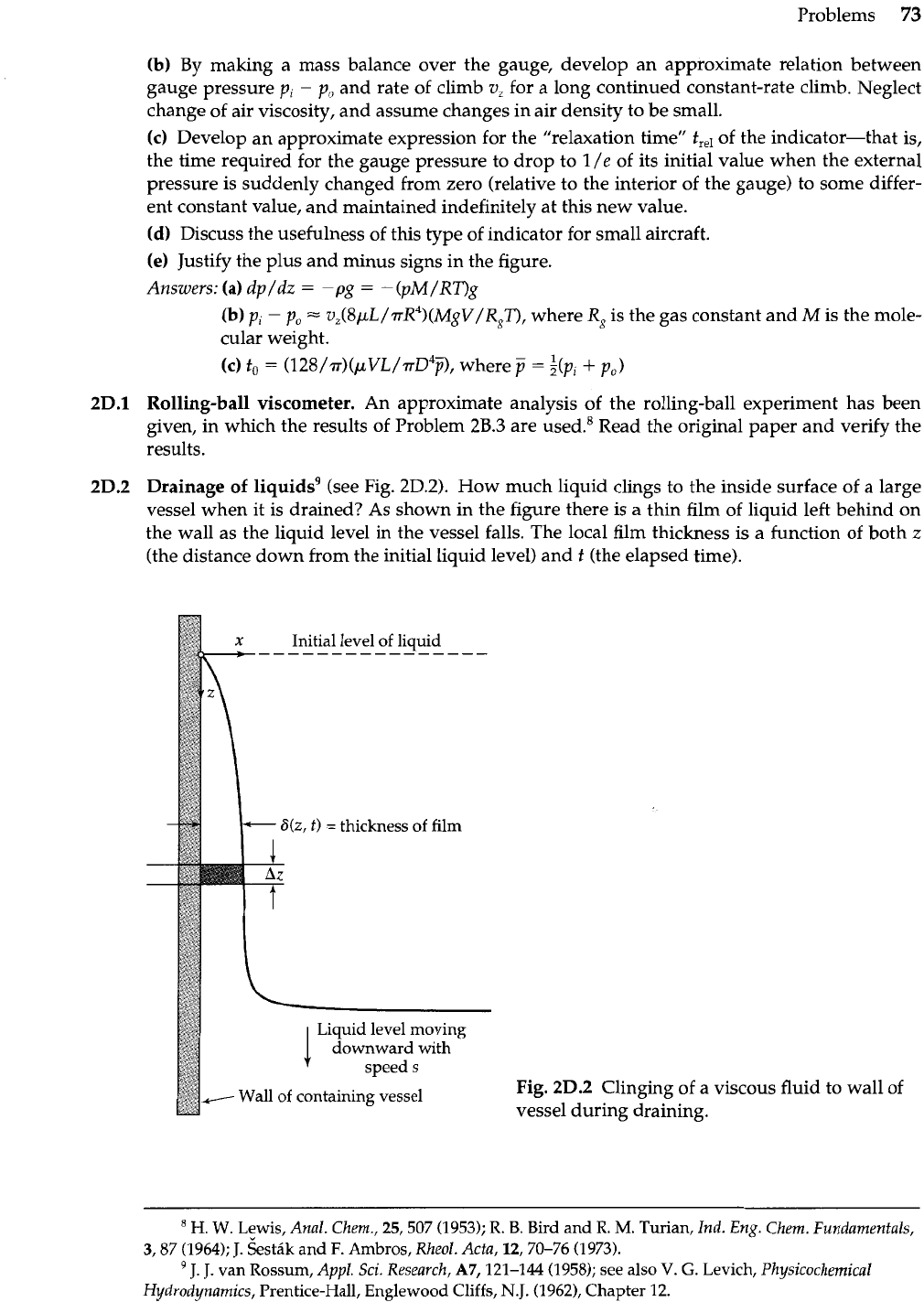
Drainage of liquids9

(see Fig. 2D.2). How much liquid clings to the inside surface of a large

vessel when it is drained? As shown in the figure there is a thin film of liquid left behind on

the wall as the liquid level in the vessel falls. The local film thickness is a function of both z

(the distance down from the initial liquid level) and

(the elapsed time).

Initial level of liquid

----------------

6(z,

thickness of film

Wall

containing vessel

Fig.

2D.2

Clinging of a viscous fluid to wall of

vessel during draining.

W. Lewis,

Anal. Chem.,

25,507 (1953); R.

Bird and

Turian,

Ind. Eng. Chem. Fundamentals,

3,87 (1964);

&stkk and

Arnbros,

Rheol. Acta,

12,70-76 (1973).

J. J.

van Rossum,

Appl. Sci. Research,

A7,121-144 (1958); see also

Levich,

Physicochemical

Hydrodynamics,

Prentice-Hall, Englewood Cliffs,

N.J.

(1962), Chapter 12.

Chapter

Shell Momentum Balances and Velocity Distributions in Laminar Flow

(a)

Make an unsteady-state mass balance on a portion of the

film

between

and

to get

(b)

Use

Eq.

2.2-18 and a quasi-steady-assumption to obtain the following first-order partial

differential equation for

6(z,

t):

(e)

Solve this equation to get

What restrictions have to be placed on this result?

Chapter

The Equations

Change

for

Isothermal Systems

3.1

The equation of continuity

93.2

The equation of motion

93.3

The equation of mechanical energy

93.4'

The equation of angular momentum

93.5

The equations of change in terms of the substantial derivative

93.6

Use of the equations of change to solve flow problems

93.7

Dimensional analysis of the equations of change

In Chapter

velocity distributions were determined for several simple flow systems by

the shell momentum balance method. The resulting velocity distributions were then

used to get other quantities, such as the average velocity and drag force. The shell bal-

ance approach was used to acquaint the novice with the notion of a momentum balance.

Even though we made no mention of it in Chapter

at several points we tacitly made

use of the idea of a mass balance.

It is tedious to set up a shell balance for each problem that one encounters. What we

need is a general mass balance and a general momentum balance that can be applied to

any problem, including problems with nonrectilinear motion. That is the main point of

this chapter. The two equations that we derive are called the

equation of continuity

(for the

mass balance) and the

equation of motion

(for the momentum balance). These equations

can be used as the starting point for studying all problems involving the isothermal flow

of a pure fluid.

In Chapter

we enlarge our problem-solving capability by developing the equa-

tions needed for nonisothermal pure fluids by adding an equation for the temperature.

In Chapter

we go even further and add equations of continuity for the concentra-

tions of the individual species. Thus as we go from Chapter

to Chapter

and on to

Chapter

we are able to analyze systems of increasing complexity, using the com-

plete set of

equations of change.

It should be evident that Chapter

is a very important

chapter-perhaps the most important chapter in the book-and it should be mastered

thoroughly.

53.1

the equation of continuity is developed by making a mass balance over a

small element of volume through which the fluid is flowing. Then the size of this ele-

ment is allowed to go to zero (thereby treating the fluid as a continuum), and the desired

partial differential equation is generated.

Chapter

The Equations of Change for Isothermal Systems

In 53.2 the equation of motion is developed by making a momentum balance over a

small element of volume and letting the volume element become infinitesimally small.

Here again a partial differential equation is generated. This equation of motion can be

used, along with some help from the equation of continuity, to set up and solve all the

problems given in Chapter

and many more complicated ones. It is thus a key equation

in transport phenomena.

In 53.3 and 53.4 we digress briefly to introduce the equations of change for mechani-

cal energy and angular momentum. These equations are obtained from the equation of

motion and hence contain no new physical information. However, they provide a conve-

nient starting point for several applications in this book-particularly the macroscopic

balances in Chapter

In 53.5 we introduce the "substantial derivative." This is the time derivative follow-

ing the motion of the substance (i.e., the fluid). Because it is widely used in books on

fluid dynamics and transport phenomena, we then show how the various equations of

change can be rewritten in terms of the substantial derivatives.

In 53.6 we discuss the solution of flow problems by use of the equations of continu-

ity and motion. Although these are partial differential equations, we can solve many

problems by postulating the form of the solution and then discarding many terms in

these equations. In this way one ends up with a simpler set of equations to solve. In this

chapter we solve only problems in which the general equations reduce to one or more

ordinary differential equations. In Chapter

we examine problems of greater complexity

that require some ability to solve partial differential equations. Then in Chapter

the

equations of continuity and motion are used as the starting point for discussing turbu-

lent flow. Later, in Chapter

these same equations are applied to flows of polymeric liq-

uids, which are non-Newtonian fluids.

Finally, 53.7 is devoted to writing the equations of continuity and motion in di-

mensionless form. This makes clear the origin of the Reynolds number, Re, often men-

tioned in Chapter 2, and why it plays a key role in fluid dynamics. This discussion lays

the groundwork for scale-up and model studies. In Chapter

dimensionless numbers

arise again in connection with experimental correlations of the drag force in complex

systems.

At the end of 52.2, we emphasized the importance of experiments in fluid dynamics.

We repeat those words of caution here and point out that photographs and other types

of flow visualization have provided us with a much deeper understanding of flow prob-

lems than would be possible by theory alone.' Keep in mind that when one derives a

flow field from the equations of change, it is not necessarily the only physically admissi-

ble solution.

Vector and tensor notations are occasionally used in this chapter, primarily for the

purpose of abbreviating otherwise lengthy expressions. The beginning student will find

that only an elementary knowledge of vector and tensor notation is needed for reading

this chapter and for solving flow problems. The advanced student will find Appendix A

helpful in getting a better understanding of vector and tensor manipulations. With re-

gard to the notation, it should be kept in mind that we use

lightface italic

symbols for

scalars,

boldface

Roman

symbols for vectors, and

boldface

Greek

symbols for tensors.

Also dot-product operations enclosed in

(

)

are scalars, and those enclosed in

I I

are

vectors.

We recommend particularly

Van

Dyke,

Album of Fluid Motion,

Parabolic Press, Stanford

(1982);

Werlk,

Ann. Rev. Fluid Mech.,

5,361-382 (1973);

Boger and

Walters,

Rheological

Phenomena

Focus,

Elsevier, Amsterdam

(1993).