Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena

Подождите немного. Документ загружается.

Problems

Table 1.7-2 Summary of Notation for Momentum Fluxes

Symbol Meaning Reference

Convective momentum-flux tensor Table 1.7-1

Viscous momentum-flux tensof Table 1.2-1

a=pti+~

Molecular momentum-flux tensorb Table 1.2-1

Combined momentum-flux tensor Eq. 1.7-2

Tor viscoelastic fluids (see Chapter

8),

this should be called the viscoelastic

momentum-flux tensor or the viscoelastic stress tensor.

This may be referred to as the molecular stress tensor.

QUESTIONS

FOR

DISCUSSION

Compare Newton's law of viscosity and Hooke's law of elasticity. What is the origin of these

"laws"?

Verlfy that "momentum per unit area per unit time" has the same dimensions as "force per

unit area."

Compare and contrast the molecular and convective mechanisms for momentum trans-

port.

What are the physical meanings of the Lennard-Jones parameters and how can they be deter-

mined from viscosity data? Is the determination unique?

How do the viscosities of liquids and low-density gases depend on the temperature and pres-

sure?

The Lennard-Jones potential depends only on the intermolecular separation. For what kinds

of molecules would you expect that this kind of potential would be inappropriate?

Sketch the potential energy function

p(r)

for rigid, nonattracting spheres.

Molecules differing only in their atomic isotopes have the same values of the Lennard-Jones

potential parameters. Would you expect the viscosity of CD, to be larger or smaller than that

of CH, at the same temperature and pressure?

Fluid

has a viscosity twice that of fluid

which fluid would you expect to flow more

rapidly through a horizontal tube of length

and radius

when the same pressure difference

is imposed?

Draw a sketch of the intermolecular force

F(r)

obtained from the Lennard-Jones function

for

&).

Also, determine the value of

r,,

in Fig. 1.4-2 in terms of the Lennard-Jones para-

meters.

What main ideas are used when one goes from Newton's law of viscosity in Eq. 1.1-2 to the

generalization in Eq. 1.2-6?

What reference works can be consulted to find out more about kinetic theory of gases and liq-

uids, and also for obtaining useful empiricisms for calculating viscosity?

PROBLEMS

lA.l Estimation of dense-gas viscosity. Estimate the

1A.2 Estimation of the viscosity of methyl fluoride. Use

viscosity of nitrogen at

68°F

and 1000 psig by means of Fig.

Fig. 1.3-1 to find the viscosity in Pa s of CH3F at 370°C and

1.3-1, using the critical viscosity from Table E.1. Give the

120 atm. Use the following values1 for the critical con-

result in units of lbm/ft

s. For the meaning of "psig," see

stants:

4.55"C,

58.0 atm,

0.300 g/cm3.

Table F.3-2.

Answer:

1.4

lbm/fte s

Kobe and

Lynn,

Jr.,

Chem.

Revs.

52,117-236 (19531,

see

202.

Chapter 1 Viscosity and the Mechanisms of Momentum Transport

1A.3

Computation of the viscosities of gases at low

density. Predict the viscosities of molecular oxygen, nitro-

gen, and methane at 20°C and atmospheric pressure, and

express the results in mPa

s. Compare the results with ex-

perimental data given in this chapter.

Answers: 0.0202,0.0172,0.0107 mPa

1A.4

Gas-mixture viscosities at low density. The fol-

lowing data2 are available for the viscosities of mixtures of

hydrogen and Freon-12

(dichlorodifluoromethane)

at 25°C

and 1 atm:

MolefractionofH,:

0.00 0.25

0.50

0.75 1.00

lo6

(poise): 124.0

128.1

131.9

135.1 88.4

Use the viscosities of the pure components to calculate the

viscosities at the three intermediate compositions by

means of Eqs. 1.4-15 and 16.

Sample answer: At 0.5,

0.01317 cp

1A.5

Viscosities of chlorine-air mixtures at low den-

sity. Predict the viscosities (in cp) of chlorine-air mixtures

at 75°F and

atm, for the following mole fractions of chlo-

rine: 0.00, 0.25, 0.50, 0.75, 1.00. Consider air as a single

component and use Eqs. 1.4-14 to 16.

Answers:

0.0183,0.0164,0.0150,0.0139,0.0130

1A.6

Estimation of liquid viscosity. Estimate the viscosity

of saturated liquid water at O°C and at lOVC by means of

(a) Eq. 1.5-9, with

AU,,

897.5 Btu/lb,,, at 100°C, and (b)

Eq. 1.5-1 1. Compare the results with the values

Table

.l-2.

Answer: (b) 4.0 cp, 0.95 cp

1A.7

Molecular velocity and mean free path. Compute

the mean molecular velocity

(in cm/s) and the mean free

path

(in cm) for oxygen at

atm and 273.2

reason-

able value for d is 3

What is the ratio of the mean free

path to the molecular diameter under these conditions?

What would be the order of magnitude of the correspond-

ing ratio in the liquid state?

Answers:

4.25

lo4

cm/s,

9.3

lo-'

lB.l Velocity profiles and the stress components

qj.

For each of the following velocity distributions, draw a

meaningful sketch showing the flow pattern. Then find all

the components of

and pvv for the Newtonian fluid. The

parameter

is a constant.

(a) v,

by, v,

0, v,

(b)

by,

bx,

(c)

-by, v,

bx, v,

(d) v,

-$bx, v,

-+by,

1B.2

fluid in a state of rigid rotation.

(a) Verify that the velocity distribution (c) in Problem lB.l

describes a fluid in a state of pure rotation; that is, the fluid

is rotating like a rigid body. What is the angular velocity of

rotation?

(b) For that flow pattern evaluate the symmetric and anti-

symmetric combinations of velocity derivatives:

(i)

(dv,/dx)

(dv,/dy)

(ii) (du,/dx)

(dv,/dy)

(c)

Discuss the results of (b) in connection with the devel-

opment in s1.2.

1B.3

Viscosity of suspensions. Data of Vand3 for sus-

pensions of small glass spheres in aqueous glycerol solu-

tions of

ZnI,

can be represented up to about

0.5 by the

semiempirical expression

Compare this result with

Eq.

1.6-2.

Answer: The Mooney equation gives a good fit of Vand's

data if

is assigned the very reasonable value of 0.70.

lC.l Some consequences of the Maxwell-Boltzmann

distribution. In the simplified kmetic theory in s1.4, sev-

eral statements concerning the equilibrium behavior of a

gas were made without proof. In this problem and the

next, some of these statements are shown to be exact

consequences of the Maxwell-Boltzmann velocity distri-

bution.

The Maxwell-Boltzmann distribution of molecular ve-

locities in an ideal gas at rest is

f(u,, u,,

u,)

n(rn/2n-~T)~'~ exp(-rnu2/2~T) (1C.1-1)

in which u is the molecular velocity, n is the number

density, and f(u,, u,, u,)du,du,du, is the number of mole-

cules per unit volume that is expected to have velocities

between

and u,

du,, u, and u,

du,.

It follows from this equation that the distribution of the

molecular speed

f (u)

4.rm~~(rn/2.rr~T)~'~ exp(-rnu2/2~T) (1C.1-2)

(a) Verify Eq. 1.4-1 by obtaining the expression for the

mean speed

from

lom

uf (u)du

(lC.1-3)

(b) Obtain the mean values of the velocity components

u,, and

The first of these is obtained from

r+m r+3o r+m

What can one conclude from the results?

Buddenberg and

Wilke,

Ind.

Eng.

Chem.

41,

1345-1347

(1949).

Vand,

Phys. Colloid Chem.,

52,277-299,300-314,

314-321 (1948).

Problems

(c)

Obtain the mean kinetic energy per molecule by

f(u)du

The correct result is

jrnz

:KT.

1C.2

The wall collision frequency. It is desired to find

the frequency

with which the molecules in an ideal gas

strike a unit area of a wall from one side only. The gas is at

rest and at equilibrium with a temperature

and the num-

ber density of the molecules is n. All molecules have a

mass

All molecules in the region x

with

will

hit an area S in the yz-plane in a short time

if they are in

the volume Su,At. The number of wall collisions per unit

area per unit time will be

J-30

Jpm

SAt

Verify the above development.

1C.3

Pressure of an ideal gas." It is desired to get the

pressure exerted by an ideal gas on a wall by accounting

for the rate of momentum transfer from the molecules to

the wall.

(a)

When a molecule traveling with a velocity v collides

with a wall, its incoming velocity components are u,,

u,, u,,

and after a specular reflection at the wall, its components

are

-u,, u,, u,.

Thus the net momentum transmitted to the

wall by a molecule is 2mux. The molecules that have an

component of the velocity equal to

u,,

and that will collide

with the wall during a small time interval At, must be

within the volume Su,At. How many molecules with ve-

locity components in the range from u,,

uy,

Au,,

Au,

will hit an area S of the wall with a ve-

locity

within a time interval At? It will be f(u,,

u,,

uJdu,

du,/u, times Su,At. Then the pressure exerted on the wall

by the gas will be

1-y

/o+m(~ux~t)(2mu,)f(uI.

u,,

u,)du~u~u,

(lC.3-1)

Explain carefully how this expression is constructed. Ver-

ify that this relation is dimensionally correct.

(b) Insert Eq. lC.l-1 for the Maxwell-Boltzmann equilib-

rium distribution into Eq. 1C.3-1 and perform the integra-

tion. Verify that this procedure leads to

~KT, the ideal

gas law.

lD.l

Uniform rotation of a fluid.

(a)

Verify that the velocity distribution in a fluid in a state

of pure rotation (i.e., rotating as a rigid body) is

rl,

where

is the angular velocity (a constant) and r is the

position vector, with components

(b) What are Vv

(Vv)+ and

for the flow field

(a)?

(c)

Interpret Eq. 1.2-7 in terms of the results in (b).

1D.2

Force on a surface of arbitrary orientatiom5 (Fig.

1D.2) Consider the material within an element of volume

OABC that is in a state of equilibrium, so that the sum of

the forces acting on the triangular faces AOBC, AOCA,

AOAB, and AABC must be zero. Let the area of AABC be

dS, and the force per unit area acting from the minus to the

plus side of dS be the vector

n,.

Show that

nl.

(a)

Show that the area of AOBC is the same as the area of

the projection AABC on the yz-plane; this is (n .6,)dS. Write

similar expressions for the areas of AOCA and AOAB.

(b)

Show that according to Table 1.2-1 the force per unit

area on AOBC is 6,.rr,,

6,~~~

6,~~~. Write similar force

expressions for AOCA and AOAB.

(c)

Show that the force balance for the volume element

OABC gives

2 2

Si)(tijaij)

z z

6,S,?r,I

(lD.2-1)

in which the indices

take on the values x,

The dou-

ble sum in the last expression is the stress tensor

written

as a sum of products of unit dyads and components.

Fig.

1D.2

Element of volume OABC over which

force

balance is made. The vector

is the force per

unit area exerted by the minus material (material inside

OABC) on the plus material (material outside OABC). The

vector n is the outwardly directed unit normal vector on

face ABC.

Silbey and

A. Alberty,

Physical Chemistry,

Wiley,

New York, 3rd edition (20011,

pp.

639-640.

Abraham and

Becker,

The Classical Theory of Electricity

and Magnetism,

Blackie and Sons, London (19521,

pp.

4445.

Chapter

Shell Momentum Balances

and Velocity Distributions

in Laminar

Flow

92.1

Shell momentum balances and boundary conditions

92.2

Flow of a falling film

92.3

Flow through a circular tube

92.4

Flow through an annulus

92.5

Flow of two adjacent immiscible fluids

92.6

Creeping flow around a sphere

In this chapter we show how to obtain the velocity profiles for laminar flows of fluids in

simple flow systems. These derivations make use of the definition of viscosity, the ex-

pressions for the molecular and convective momentum fluxes, and the concept of a mo-

mentum balance. Once the velocity profiles have been obtained, we can then get other

quantities such as the maximum velocity, the average velocity, or the shear stress at a

surface. Often it is these latter quantities that are of interest in engineering problems.

In the first section we make a few general remarks about how to set up differential

momentum balances. In the sections that follow we work out in detail several classical

examples of viscous flow patterns. These examples should be thoroughly understood,

since we shall have frequent occasions to refer to them in subsequent chapters. Although

these problems are rather simple and involve idealized systems, they are nonetheless

often used in solving practical problems.

The systems studied in this chapter are so arranged that the reader is gradually in-

troduced to a variety of factors that arise in the solution of viscous flow problems. In 52.2

the falling film problem illustrates the role of gravity forces and the use of Cartesian co-

ordinates; it also shows how to solve the problem when viscosity may be a function of

position. In 52.3 the flow in a circular tube illustrates the role of pressure and gravity

forces and the use of cylindrical coordinates; an approximate extension to compressible

flow is given. In 52.4 the flow in a cylindrical annulus emphasizes the role played by the

boundary conditions. Then in 52.5 the question of boundary conditions is pursued fur-

ther in the discussion of the flow of two adjacent immiscible liquids. Finally, in

92.6

the

flow around a sphere is discussed briefly to illustrate a problem in spherical coordinates

and also to point out how both tangential and normal forces are handled.

The methods and problems in this chapter apply only to

steady

flow.

By "steady" we

mean that the pressure, density, and velocity components at each point in the stream do

not change with time. The general equations for unsteady flow are given in Chapter 3.

2.1

Shell Momentum Balances and Boundary Conditions

Fluid

containing

tiny particles

Fig.

2.0-1

(a)

Laminar flow, in which fluid

layers move smoothly over one another in

the direction of flow, and

(b)

turbulent

flow, in which the flow pattern is complex

Direction

(a)

O-L~)

of flow

and time-dependent, with considerable

motion perpendicular to the principal flow

direction.

This chapter is concerned only with

laminar

flow. "Laminar flow" is the orderly flow

that is observed, for example, in tube flow at velocities sufficiently low that tiny particles

injected into the tube move along in a thin line. This is in sharp contrast with the wildly

chaotic "turbulent flow" at sufficiently high velocities that the particles are flung apart

and dispersed throughout the entire cross section of the tube. Turbulent flow is the sub-

ject of Chapter

The sketches in Fig. 2.0-1 illustrate the difference between the two flow

regimes.

2.1

SHELL MOMENTUM BALANCES AND BOUNDARY

CONDITIONS

The problems discussed in 52.2 through 52.5 are approached by setting up momentum

balances over a thin "shell" of the fluid. For

steady

pow, the momentum balance is

[te momentum of in

]

[rate of

momentum out momentum in momentum out force of gravity

by convective by convective by molecular by molecular acting on system

transport transport transport transport

This is a restricted statement of the law of conservation of momentum. In this chapter we

apply this statement only to one component of the momentum-namely, the component

in the direction of flow. To write the momentum balance we need the expressions for the

convective momentum fluxes given in Table 1.7-1 and the molecular momentum fluxes

given in Table 1.2-1; keep in mind that the molecular momentum flux includes both the

pressure and the viscous contributions.

In this chapter the momentum balance is applied only to systems in which there is

just one velocity component, which depends on only one spatial variable; in addition,

the flow must be rectilinear. In the next chapter the momentum balance concept is ex-

tended to unsteady-state systems with curvilinear motion and more than one velocity

component.

The procedure in this chapter for setting up and solving viscous flow problems is as

follows:

Identify the nonvanishing velocity component and the spatial variable on which it

depends.

Write a momentum balance of the form of Eq. 2.1-1 over a thin shell perpendicular

to the relevant spatial variable.

Let the thickness of the shell approach zero and make use of the definition of the first

derivative to obtain the corresponding differential equation for the momentum flux.

Chapter

Shell Momentum Balances and Velocity Distributions in Laminar Flow

Integrate this equation to get the momentum-flux distribution.

Insert Newton's law of viscosity and obtain a differential equation for the velocity.

Integrate this equation to get the velocity distribution.

Use the velocity distribution to get other quantities, such as the maximum veloc-

ity, average velocity, or force on solid surfaces.

In the integrations mentioned above, several constants of integration appear, and these

are evaluated by using "boundary conditionsu-that is, statements about the velocity or

stress at the boundaries of the system. The most commonly used boundary conditions

are as follows:

solid-fluid

interfaces the fluid velocity equals the velocity with which the solid

surface is moving; this statement is applied to both the tangential and the normal

component of the velocity vector. The equality of the tangential components is

referred to as the "no-slip condition.''

At a

liquid-liquid

interfacial plane of constant

the tangential velocity compo-

nents

and

are continuous through the interface (the "no-slip condition") as

are also the molecular stress-tensor components

T,,,

rxy,

and

T,,.

At a

liquid-gas

interfacial plane of constant

the stress-tensor components

T,,

and

T,,

are taken to be zero, provided that the gas-side velocity gradient is not too

large. This is reasonable, since the viscosities of gases are much less than those of

liquids.

In all of these boundary conditions it is presumed that there is no material passing

through the interface; that is, there is no adsorption, absorption, dissolution, evapora-

tion, melting, or chemical reaction at the surface between the two phases. Boundary con-

ditions incorporating such phenomena appear in Problems

3C.5

and llC.6, and 518.1.

In this section we have presented some guidelines for solving simple viscous flow

problems. For some problems slight variations on these guidelines may prove to be

appropriate.

92.2

FLOW OF A FALLING

FILM

The first example we discuss is that of the flow of a liquid down an inclined flat plate of

length

and width

as shown in Fig. 2.2-1. Such films have been studied in connection

with wetted-wall towers, evaporation and gas-absorption experiments, and applications

of coatings. We consider the viscosity and density of the fluid to be constant.

A complete description of the liquid flow is difficult because of the disturbances at

the edges of the system

W).

An adequate description can often be

Entrance disturbance

Liquid

FA-

film Liquid in

Keservoir

Exit disturbance

-66

Direction of

gravity

Fig.

2.2-1

Schematic

diagram of the falling

film experiment, show-

ing end effects.

g2.2 Flow of a Falling Film

obtained by neglecting such disturbances, particularly if

and

are large compared to

the film thickness

For small flow rates we expect that the viscous forces will prevent

continued acceleration of the liquid down the wall, so that v, will become independent

of z in a short distance down the plate. Therefore it seems reasonable to

postulate

that

v,(x),

and

0, and further that p

p(x). From Table

B.l

it is seen that the

only nonvanishing components of

are then

T,,

-p(dv,/dx).

We now select as the "system" a thin shell perpendicular to the

direction (see Fig.

2.2-2). Then we set up a z-momentum balance over this shell, which is a region of thick-

ness Ax, bounded by the planes z

and

and extending a distance Win the

di-

rection. The various contributions to the momentum balance are then obtained with the

help of the quantities in the "z-component" columns of Tables 1.2-1 and 1.7-1. By using

the components of the "combined momentum-flux tensor"

defined in 1.7-1 to

can include all the possible mechanisms for momentum transport at once:

rate of z-momentum in

across surface at z

(WAX)+~~L=O

rate of z-momentum out

across surface at

(WAX)&I,=L

rate of z-momentum in

across surface at x

(LW(+xz)Ix

rate of z-momentum out

across surface at x

(LW(4~~)I~+~~

gravity force acting

on fluid

the z direction

Ax)(pg

cos

By using the quantities

+,,

and

+,,

we account for the z-momentum transport by all

mechanisms, convective and molecular. Note that we take the "in" and "out" directions

in the direction of the positive x- and z-axes (in this problem these happen to coincide

with the directions of z-momentum transport). The notation

I,,,,

means "evaluated at

Ax," and g is the gravitational acceleration.

When these terms are substituted into the z-momentum balance of

Eq.

2.1-1, we get

Direction

z=L

gravity

Fig.

2.2-2

Shell of thickness

over which a z-momentum balance is made. Arrows show the

momentum fluxes associated with the surfaces of the shell. Since

and

are both zero, pvxvz

and

pvp,

are zero. Since

does not depend on

and

it follows from Table

B.l

that

T,,

and

T,,

Therefore, the dashed-underlined fluxes do not need to be considered. Both

and pv,v, are the same at

and

and therefore do not appear in the final equation

for the balance of z-momentum,

Eq.

2.2-10.

Chapter 2

Shell Momentum Balances and Velocity Distributions in Laminar Flow

When this equation is divided by

Ax, and the limit taken as Ax approaches zero, we

get

The first term on the left side is exactly the definition of the derivative of

4,:

with respect

Therefore Eq. 2.2-7 becomes

At this point we have to write out explicitly what the components

+,,

and

4,:

are, mak-

ing use of the definition of

in Eqs. 1.7-1 to

and the expressions for

rxz

and

T,,

in Ap-

pendix

B.1.

This ensures that we do not miss out on any of the forms of momentum

transport. Hence we get

In accordance with the postulates that v,

v,(x),

0, v,

0, and

p(x), we see that

(i) since v,

0, the pup, term in Eq. 2.2-9a is zero; (ii) since v,

v,(x), the term

-2,u(dv,/dz) in Eq. 2.2-9b is zero; (iii) since v,

v,(x), the term pv,v, is the same at z

and z

and (iv) since p

p(x), the contribution p is the same at

0 and z

Hence

T,,

depends only on x, and Eq. 2.2-8 simplifies to

cos

This is the differential equation for the momentum flux

T,,.

It may be integrated to give

The constant of integration may be-evaluated by using the boundary condition at the

gas-liquid interface (see 52.1):

B.C.

1: atx=O, r,,=O (2.2-12)

Substitution of this boundary condition into Eq. 2.2-11 shows that

0. Therefore the

momentum-flux distribution is

as shown in Fig. 2.2-3.

Next we substitute Newton's law of viscosity

into the left side of Eq. 2.2-13 to obtain

which is the differential equation for the velocity distribution. It can be integrated to

give

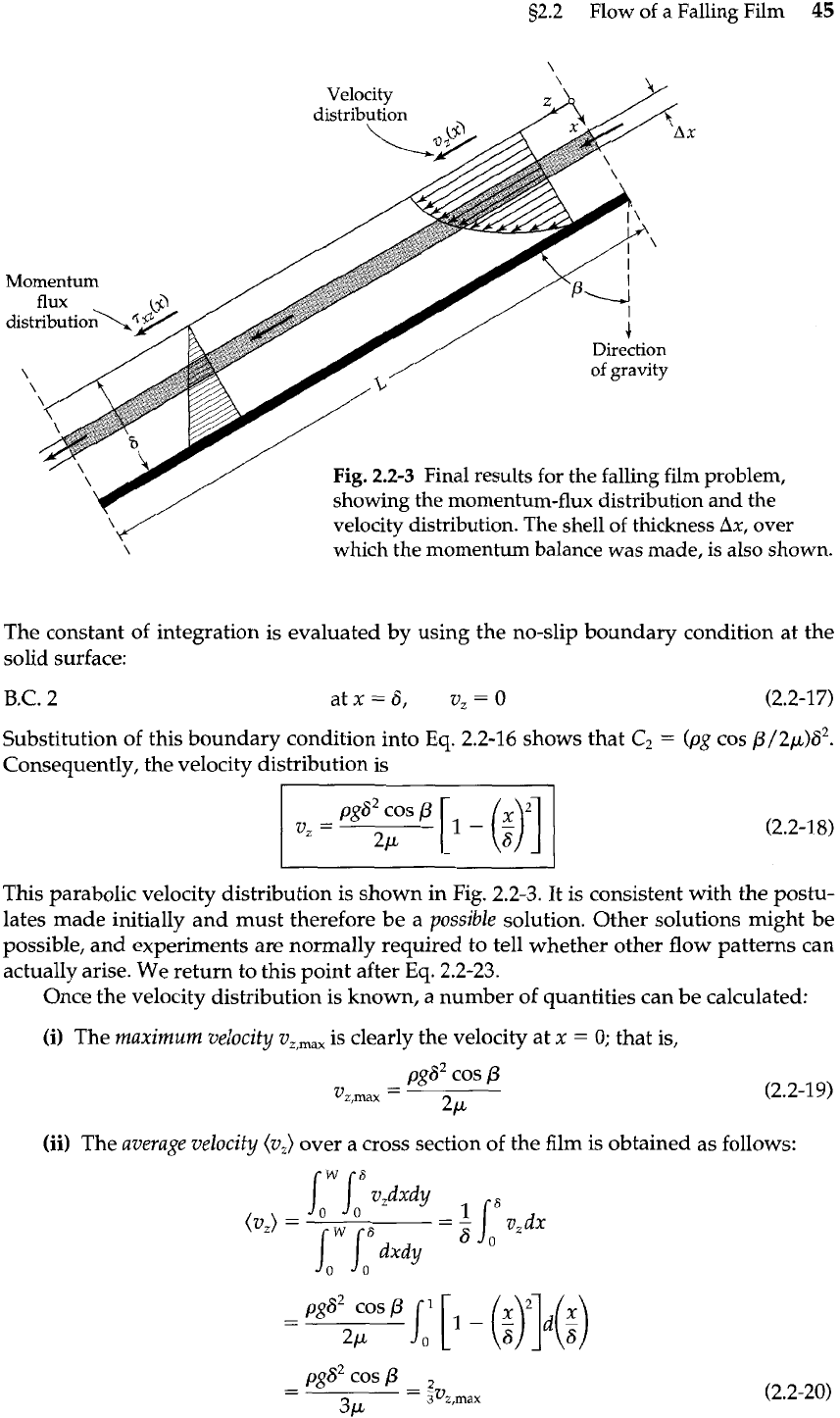
52.2

Flow of a Falling Film

Momentum

Fig.

2.2-3

Final results for the falling film problem,

showing the momentum-flux distribution and the

velocity distribution. The shell of thickness

Ax,

over

which the momentum balance was made, is also shown.

The constant of integration is evaluated by using the no-slip boundary condition at the

solid surface:

B.C.

(2.2-17)

Substitution of this boundary condition into

Eq.

2.2-16

shows that

(pg

cos

P/24a2.

Consequently, the velocity distribution is

This parabolic velocity distribution is shown in Fig. 2.2-3. It is consistent with the postu-

lates made initially and must therefore be a

possible

solution. Other solutions might be

possible, and experiments are normally required to tell whether other flow patterns can

actually arise. We return to this point after Eq.

2.2-23.

Once the velocity distribution is known, a number of quantities can be calculated:

(i)

The

maximum velocity vZ,,,,

is clearly the velocity at

that is,

(ii)

The

average velocity (v,)

over a cross section of the film is obtained as follows:

Chapter 2

Shell Momentum Balances and Velocity Distributions

Laminar Flow

The double integral in the denominator of the first line is the cross-sectional area of the

film. The double integral in the numerator is the volume flow rate through a differential

element of the cross section,

v,dx

dy,

integrated over the entire cross section.

(iii)

The

mass rate of flow

is obtained from the average velocity or by integration of

the velocity distribution

p2g

ws3

cos

low

IO8

pv,dxdy

pWS(v,)

(iv)

The

film thickness

may be given in terms of the average

rate of flow as follows:

(2.2-21)

velocity or the mass

(v)

The force per unit area in the z direction on a surface element perpendicular

to the

direction is

+T,,

evaluated at

This is the force exerted by the fluid (re-

gion of lesser

on the wall (region of greater

x).

The z-component of the

force

of the

fluid on the solid surface

is obtained by integrating the shear stress over the fluid-solid

interface:

This is the z-component of the weight of the fluid in the entire film-as we would have

expected.

Experimental observations of falling films show that there are actually three "flow

regimes," and that these may be classified according to the

Reynolds number,'

Re, for the

flow. For falling films the Reynolds number is defined by Re

4S(vz)p/p.

The three flow

regime are then:

laminar flow with negligible rippling

laminar flow with pronounced rippling

1500

turbulent flow Re

1500

The analysis we have given above is valid only for the first regime, since the analysis

was restricted by the postulates made at the outset. Ripples appear on the surface of the

fluid at all Reynolds numbers. For Reynolds numbers less than about 20, the ripples are

very long and grow rather slowly as they travel down the surface of the liquid; as a re-

sult the formulas derived above are useful up to about Re

20 for plates of moderate

length. Above that value of Re, the ripple growth increases very rapidly, although the

flow remains laminar. At about Re

1500 the flow becomes irregular and chaotic, and

the flow is said to be t~rbulent.~,~ At this point it is not clear why the value of the

'This dimensionless group is named for

Osbome

~e~nblds

(1842-19121,

professor of engineering at

the University of Manchester. He studied the laminar-turbulent transition, turbulent heat transfer, and

theory of lubrication.

shall see in the next chapter that the Reynolds number is the ratio

the inertial

forces to the viscous forces.

Fulford,

Adv. Chem. Engr.,

5,151-236 (1964);

Whitaker,

Ind.

Eng.

Chem. Fund.,

3,132-142

(1964);

Levich,

Physicochemical Hydrodynamics,

Prentice-Hall, Englewood Cliffs,

N.J.

(1962), s135.

H.-C. Chang,

Ann.

Rev. Fluid Mech.,

26,103-136 (1994);

S.-H.

Hwang and H.-C. Chang,

Phys. Fluids,

30,1259-1268 (1987).