Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena
Подождите немного. Документ загружается.


12
Generalization of Newton's Law of Viscosity
17
any instant of time we can slice the volume element in such a way as to remove half the
fluid within it. As shown in the figure, we can cut the volume perpendicular to each of
the three coordinate directions in turn. We can then ask what force has to be applied on
the free (shaded) surface in order to replace the force that had been exerted on that sur-
face by the fluid that was removed. There will be two contributions to the force: that as-
sociated with the pressure, and that associated with the viscous forces.
The pressure force will always be perpendicular to the exposed surface. Hence in (a)
the force per unit area on the shaded surface will be a vector p6,-that is, the pressure (a
scalar) multiplied by the unit vector 6, in the x direction. Similarly, the force on the
shaded surface in
(b)
will be p6,, and in
(c)
the force will be p6,. The pressure forces will
be exerted when the fluid is stationary as well as when it is in motion.
The viscous forces come into play only when there are velocity gradients within the
fluid.
In
general they are neither perpendicular to the surface element nor parallel to it,
but rather at some angle to the surface (see Fig. 1.2-1). In (a) we see a force per unit area
T,
exerted on the shaded area, and in
(b)
and
(c)
we see forces per unit area
T,
and
7,.
Each of these forces (which are vectors) has components (scalars); for example,
T,
has
components
T,,,
T,~,
and
T,,.
Hence we can now summarize the forces acting on the three
shaded areas in Fig.
1.2-1
in Table
1.2-1.
This tabulation is a summary of the forces per
unit area (stresses) exerted within a fluid, both by the thermodynamic pressure and the
viscous stresses. Sometimes we will find it convenient to have a symbol that includes both
types of stresses, and so we define the molecular stresses as follows:
r
.
=
paii
+
rii
where
i
and
j
may be x,
y,
or
z
'I
(1.2-2)
Here
Sij
is the Kronecker delta, which is
1
if
i
=
j
and zero if
i
#
j.
Just as in the previous section, the r,j (and also the
'rr$
may be interpreted in two ways:
rZi
=
pa,,
+
ril
=
force in the
j
direction on a unit area perpendicular to the
i
direction,
where it is understood that the fluid in the region of lesser xi is exerting
the force on the fluid of greater xi
'rrY
=
paij
+
rij
=
flux of j-momentum in the positive
i
direction-that is, from the region
of lesser
xi
to that of greater xi
Both interpretations are used in this book; the first one is particularly useful in describ-
ing the forces exerted by the fluid on solid surfaces. The stresses
.rr,,
=
p
+
T,,,
5,
=
p
+
ryy,
'rrzz
=
p
+
T,,
are called normal stresses, whereas the remaining quantities,
IT,,
=
T,,,
5,
=
T~~,
. .
.
are called shear stresses. These quantities, which have two subscripts associ-
ated with the coordinate directions, are referred to as "tensors," just as quantities (such
as velocity) that have one subscript associated with the coordinate directions are called
Table
1.2-1
Summary of the Components of the Molecular Stress Tensor (or Molecular
Momentum-Flux Tensor)"
Direction
normal
to the
shaded
Vector force
per unit area on the
shaded face (momentum
face flux through shaded face)
X
Tr,
=
pajx
+
Tw
Y
n,
=
p6,
+
T,
z
m,
=
p6,
+
T,
Components of the forces (per unit area)
acting on the shaded face (components of the
momentum flux through the shaded face)
x-component y-component z-component
"
These are referred to as components of the "molecular momentum flux tensor" because they are
associated with the molecular motions, as discussed in
g1.4
and Appendix
D.
The additional "convective
momentum flux tensor" components, associated with bulk movement of the fluid, are discussed in
51.7.

18
Chapter
1
Viscosity and the Mechanisms of Momentum Transport
I,
vectors." Therefore we will refer to
T
as the z~iscous stress tensor (with components
T~)
and
.rr
as the molecular stress tensor (with components
qj).
When there is no chance for
confusion, the modifiers "viscous" and "molecular" may be omitted.
A
discussion of
vectors and tensors can be found
in
Appendix A.
The question now is: How are these stresses rij related to the velocity gradients in
the fluid? In generalizing Eq. 1.1-2, we put several restrictions on the stresses, as follows:
The viscous stresses may be linear combinations of all the velocity gradients:
dvk
7..
=
-CkClp..
-
where
i,
j,
k,
and
1
may be 1,2,3 (1.2-3)
11
vk'
dx1
Here the 81 quantities
pijkl
are "viscosity coefficients." The quantities x,, x,, x3 in
the derivatives denote the Cartesian coordinates x,
y,
z, and v,, v,,
v,
are the same
as v,, v,, v,.
We assert that time derivatives or time integrals should not appear in the expres-
sion. (For viscoelastic fluids, as discussed in Chapter 8, time derivatives or time in-
tegrals are needed to describe the elastic responses.)
We do not expect any viscous forces to be present, if the fluid is in a state of pure
rotation. This requirement leads to the necessity that
ri,
be a symmetric combina-
tion of the velocity gradients. By this we mean that if
i
and
j
are interchanged, the
combination of velocity gradients remains unchanged. It can be shown that the
only symmetric linear combinations of velocity gradients are
If the fluid is isotropic-that is, it has no preferred direction-then the coefficients
in front of the two expressions in
Eq.
1.2-4 must be scalars so that
We have thus reduced the number of "viscosity coefficients" from 81 to 2!
Of course, we want Eq. 1.2-5 to simplify to Eq. 1.1-2 for the flow situation in Fig.
1.1-1. For that elementary flow Eq. 1.2-5 simplifies to
T,,
=
A
dv,/dy, and hence the
scalar constant
A
must be the same as the negative of the viscosity
p.
Finally, by common agreement among most fluid dynamicists the scalar constant
B
is set equal to
$p
-
K,
where
K
is called the dilatational viscosity. The reason for
writing
B
in this way is that it is known from kinetic theory that
K
is identically
zero for monatomic gases at low density.
Thus the required generalization for Newton's law of viscosity in Eq. 1.1-2 is then
the set of nine relations (six being independent):
Here
T~~
=
T,~,
and
i
and
j
can take on the values 1,2,3. These relations for the stresses in a
Newtonian fluid are associated with the names of Navier, Poisson, and ~tokes.~ If de-
'
C.-L.-M.-H.
Navier,
Ann.
Chimie,
19,244-260 (1821);
S.-D.
Poisson,
I.
~cole Polytech.,
13,
Cahier 20,l-174
(1831);
G. G.
Stokes,
Trans.
Camb.
Phil. Soc.,
8,287-305 (1845).
Claude-Louis-Marie-Henri
Navier
(1785-1836)
(pronounced "Nah-vyay," with the second syllable accented) was a civil engineer whose specialty was road
and bridge building;
George Gabriel Stokes
(1819-1903) taught at Cambridge University and was president
of the Royal Society. Navier
and
Stokes are well known because of the Navier-Stokes equations (see Chapter
3).
See
also
D.
J.
Acheson,
Elemazta
y
Fluid Mechanics,
Oxford University Press (1990), pp. 209-212,218.

1.2 Generalization of Newton's Law of Viscosity
19
sired, this set of relations can be written more concisely in the vector-tensor notation of
Appendix A as
in which
6
is the unit tensor with components
SV,
Vv is the velocity gradient tensor with
components (d/dxi)vj,
(Vv)'
is the "transposer' of the velocity gradient tensor with com-
ponents (d/dxj)vi, and
(V
.
v) is the divergence of the velocity vector.
The important conclusion is that we have a generalization of Eq. 1.1-2, and this gen-
eralization involves not one but two coefficients3 characterizing the fluid: the viscosity
p
and the dilatational viscosity
K.
Usually, in solving fluid dynamics problems, it is not
necessary to know
K.
If the fluid is a gas, we often assume it to act as an ideal
monoatomic gas, for which
K
is identically zero. If the fluid is a liquid, we often assume
that it is incompressible, and in Chapter
3
we show that for incompressible liquids
(V
v)
=
0,
and therefore the term containing
K
is discarded anyway. The dilational vis-
cosity is important
in
describing sound absorption in polyatomic gases4 and in describ-
ing the fluid dynamics of liquids containing gas
bubble^.^
Equation 1.2-7 (or 1.2-6) is an important equation and one that we shall use often.
Therefore it is written out in full in Cartesian (x,
y,
z), cylindrical (r,
8,
z), and spherical
(r,
Of+)
coordinates in Table
B.1.
The entries in this table for curvilinear coordinates are
obtained by the methods outlined
in
55A.6 and
A.7.
It is suggested that beginning stu-
dents not concern themselves with the details of such derivations, but rather concen-
trate on using the tabulated results. Chapters
2
and
3
will give ample practice in doing
this.
In curvilinear coordinates the stress components have the same meaning as in Carte-
sian coordinates. For example,
r,,
in cylindrical coordinates, which will be encountered
in Chapter
2,
can be interpreted as:
(i)
the viscous force in the z direction on a unit area
perpendicular to the r direction, or (ii) the viscous flux of z-momentum in the positive r
direction. Figure 1.2-2 illustrates some typical surface elements and stress-tensor compo-
nents that arise in fluid dynamics.
The shear stresses are usually easy to visualize, but the normal stresses may cause
conceptual problems. For example,
T,,
is a force per unit area in the z direction on a
plane perpendicular to the z direction. For the flow of an incompressible fluid in the
convergent channel of Fig. 1.2-3, we know intuitively that v, increases with decreas-
ing z; hence, according to Eq. 1.2-6, there is a nonzero stress
r,,
=
-2p(dv,/dz) acting
in the fluid.
Note on the Sign Convention for the Stress Tensor We have emphasized in connection
with Eq. 1.1-2 (and in the generalization in this section) that
T~~
is the force in the posi-
tive x direction on a plane perpendicular to the
y
direction, and that this is the force ex-
erted by the fluid in the region of the lesser
y
on the fluid of greater
y.
In most fluid
dynamics and elasticity books, the words "lesser" and "greater" are interchanged and
Eq. 1.1-2 is written as
r,,
=
+p(dv,/dy). The advantages of the sign convention used in
this book are: (a) the sign convention used in Newton's law of viscosity is consistent
with that used in Fourier's law of heat conduction and Fick's law of diffusion; (b) the
sign convention for
rij
is the same as that for the convective momentum flux
pw
(see
Some writers refer to
p
as the "shear viscosity," but this is inappropriate nomenclature inasmuch
as
p
can arise
in
nonshearing flows as well as shearing flows. The term "dynamic viscosity" is also
occasionally seen, but this term has a very specific meaning in the field
of
viscoelasticity and is an
inappropriate term
for
p.
L.
Landau and
E.
M.
Lifshitz,
op. cit.,
Ch.
VIII.
G.
K.
Batchelor,
An Introduction to Fluid Dynamics,
Cambridge University Press
(1963,
pp.
253-255.
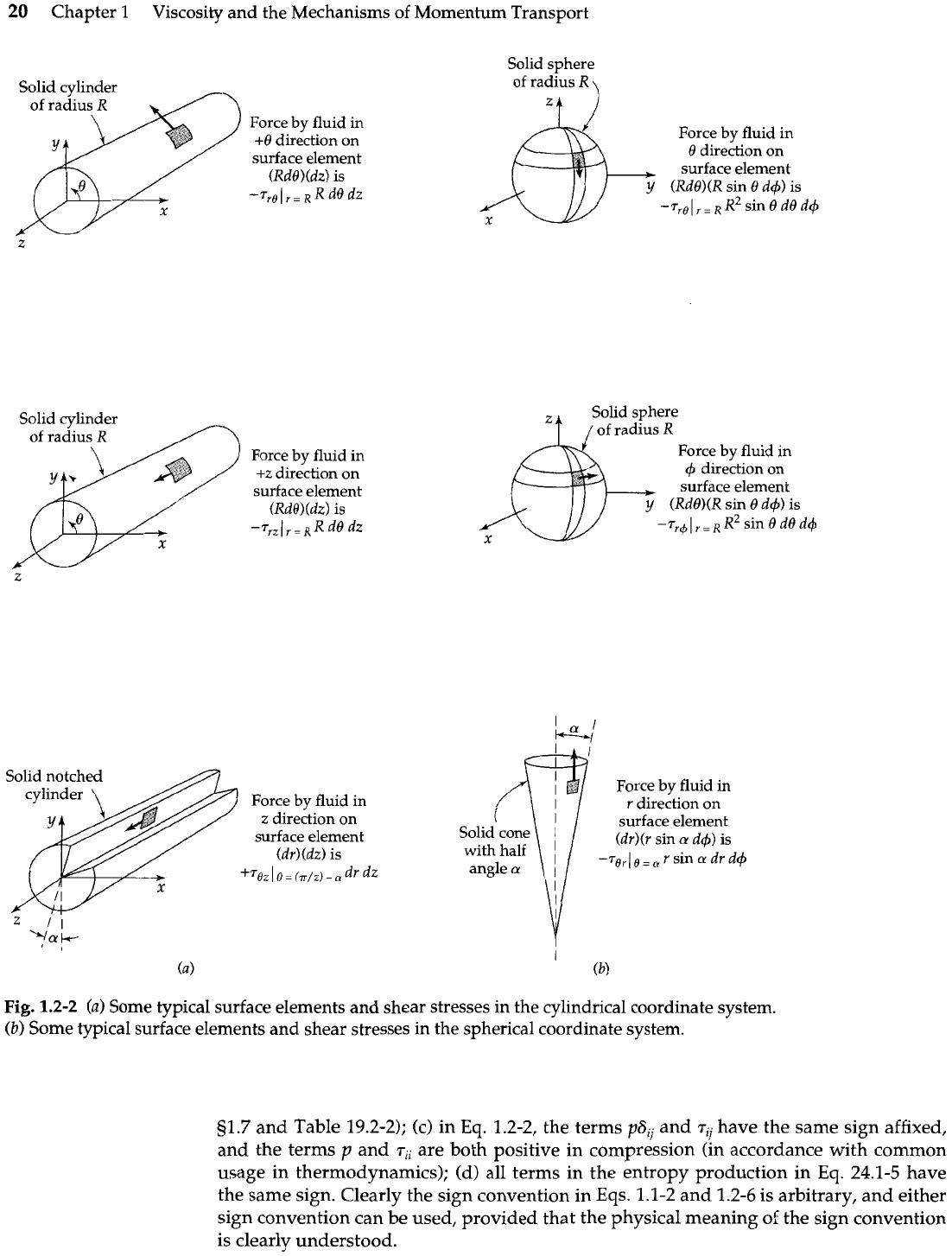
20
Chapter
1
Viscosity and the Mechanisms of Momentum Transport
of radius
R
Force
by
fluid in
+8
direction on
surface element
(RdB)(dz)
is
-~~o(~=RRdedz
Z
surface element
(RdNdz)
is
-7,.,(,.=~Rd~d~
Z
Solid notched
Force
by
fluid
in
z
direction on
surface element
(dr)(dz)
is
+To2
1
o
=
(,/zI
-
,
dr dz
/I
Yak
'
I
Solid sphere
of radius
R
Force
by
fluid in
8
direction on
surface element
(RdB)(R
sin
8 d4)
is
-rrolr=R~2sin0d8d4
Solid sphere
of radius
R
Force
by
fluid in
4
direction on
surface element
(RdMR
sin
8 d4)
is
-T~+~~=~R~
sin
8 d8d4
I
Force
by
fluid in
r
direction on
surface element
Solid cone
(dr)(r
sin
a
d+)
is
with half
-
ror(o=ar
sin
ru
drd4
Fig.
1.2-2
(a)
Some typical surface elements and shear stresses in the cylindrical coordinate system.
(b)
Some typical surface elements and shear stresses in the spherical coordinate system.
51.7
and Table 19.2-2); (c) in Eq.
1.2-2,
the terms
paij
and
T~~
have the same sign affixed,
and the terms
p
and
T~~
are both positive in compression (in accordance with common
usage in thermodynamics); (d) all terms in the entropy production in
Eq.
24.1-5 have
the same sign. Clearly the sign convention in Eqs.
1.1-2
and 1.2-6 is arbitrary, and either
sign convention
can
be used, provided that the physical meaning of the sign convention
is clearly understood.

3 Pressure and Temperature Dependence of Viscosity
21
Fig.
1.2-3
The flow in a converging duct is an example of a situation
in which the normal stresses are not zero. Since
v,
is a function of
r
and
z,
the normal-stress component
T,,
=
-2p(dv,/dz)
is nonzero.
Also, since
v,
depends on
r
and
z,
the normal-stress component
T,,
=
-2p(dvr/dr)
is not equal to zero. At the wall, however, the
'z")
normal stresses all vanish far fluids described by Eq.
1.2-7
provided
that the density is constant (see Example 3.1-1 and Problem
3C.2).
1.3
PRESSURE AND TEMPERATURE DEPENDENCE
OF VISCOSITY
Extensive data on viscosities of pure gases and liquids are available in various science
and engineering handbooks.' When experimental data are lacking and there is not time
to obtain them, the viscosity can be estimated by empirical methods, making use of other
data on the given substance. We present here a corresponding-states correlation, which fa-
cilitates such estimates and illustrates general trends of viscosity with temperature and
pressure for ordinary fluids. The principle of corresponding states, which has a sound
scientific basis: is widely used for correlating equation-of-state and thermodynamic
data. Discussions of this principle can be found in textbooks on physical chemistry and
thermodynamics.
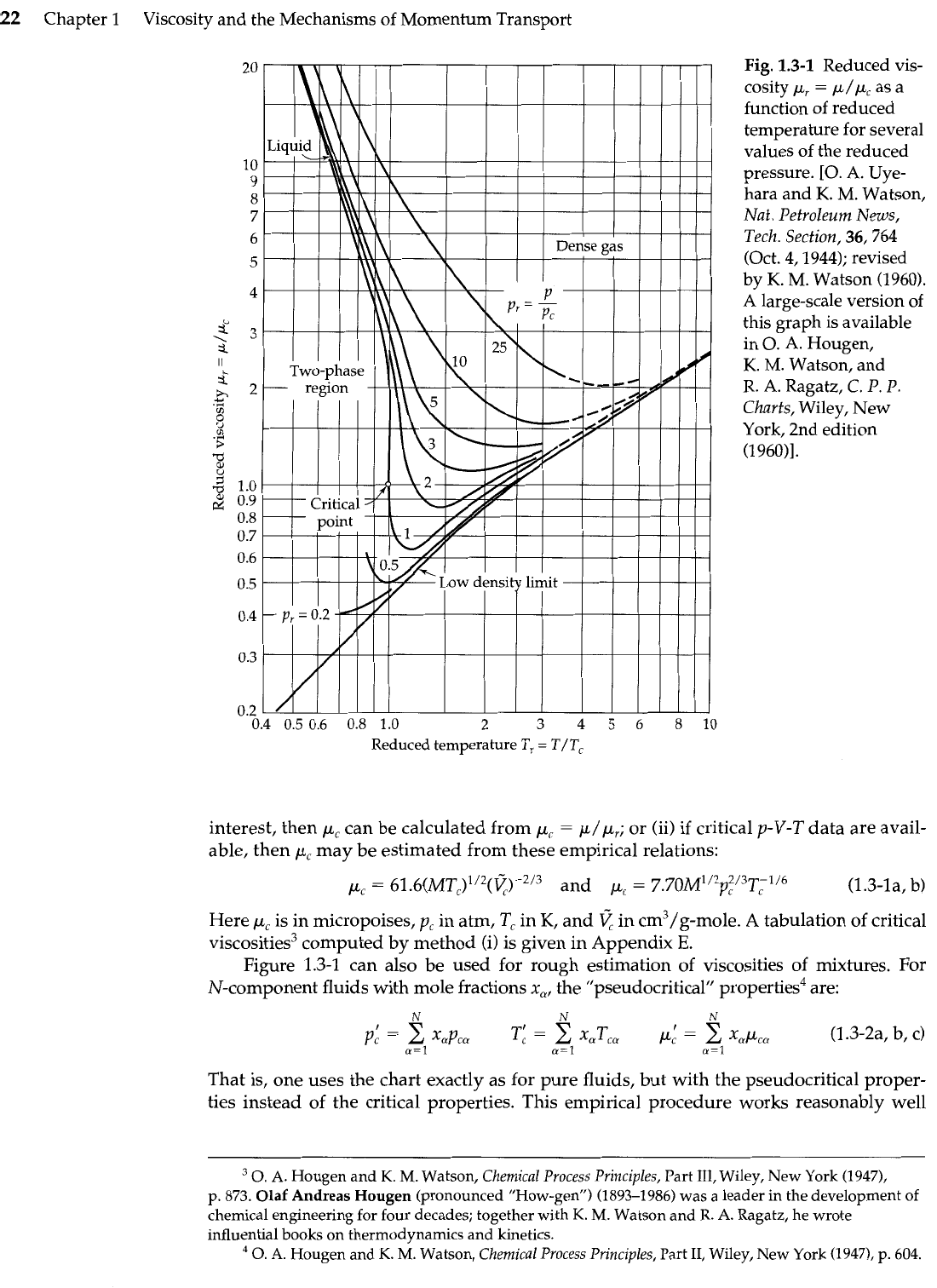
The plot in Fig. 1.3-1 gives a global view of the pressure and temperature dependence
of viscosity. The reduced viscosity
pr
=
p/p,
is plotted versus the reduced temperature
T,
=
T/T,
for various values of the reduced pressure
p,
=
p/p,.
A
"reduced quantity is one
that has been made dimensionless by dividing by the corresponding quantity at the criti-
cal point. The chart shows that the viscosity of a gas approaches a limit (the low-density
limit) as the pressure becomes smaller; for most gases, this limit is nearly attained at
1
atm
pressure. The viscosity of a gas at low density increases with increasing temperature,
whereas the viscosity of
a
liquid decreases with increasing temperature.
Experimental values of the critical viscosity
p,
are seldom available. However,
p,
may be estimated in one of the following ways: (i) if a value of viscosity is known at a
given reduced pressure and temperature, preferably at conditions near to those of
-
-
--
J.
A.
Schetz and
A.
E.
Fuhs (eds.),
Handbook of Fluid Dynamics and Fluid Machinery,
Wiley-
Interscience, New York (1996), Vol. 1, Chapter
2;
W. M. Rohsenow,
J.
P.
Hartnett, and Y.
I.
Cho,
Handbook
of Heat Transfer,
McGraw-Hill, New York, 3rd edition (19981, Chapter
2.
Other sources are mentioned in
fn.
4
of 91.1.
J.
Millat,
J.
H.
Dymond, and C.
A.
Nieto de Castro (eds.),
Transport Properties of Fluids,
Cambridge
University Press (1996), Chapter
11,
by
E.
A.
Mason and
F.
J.
Uribe, and Chapter
12,
by
M.
L.
Huber
and
H.
M.
M.
Hanley.
22
Chapter 1 Viscosity and the Mechanisms of Momentum Transport
Fig.
1.3-1 Reduced vis-
cosity
pr
=
p/p,
as a
function of reduced
temperature for several
values of the reduced
pressure.
10.
A.
Uye-
hara and
K.
M.
Watson,
Nat. Petroleum News,
Tech. Section, 36,764
(Oct. 4,1944); revised
by
K.
M. Watson (1960).
A
large-scale version of
this graph is available
in
0.
A.
Hougen,
K.
M.
Watson, and
R.
A.
Ragatz,
C.
P. P.
Charts, Wiley, New
York, 2nd edition
(1960)l.
Reduced temperature
T,
=
T/T,
interest, then
pc
can be calculated from
p,
=
p/pY; or (ii) if critical p-V-T data are avail-
able, then p, may be estimated from these empirical relations:
Here
p,
is in micropoises, p, in atm, Tc in
K,
and
in cm3/g-mole. A tabulation of critical
viscosities3 computed by method (i) is given in Appendix
E.
Figure 1.3-1 can also be used for rough estimation of viscosities of mixtures. For
N-component fluids with mole fractions x,, the "pseudocritical" properties4 are:
That is, one uses the chart exactly as for pure fluids, but with the pseudocritical proper-
ties instead of the critical properties. This empirical procedure works reasonably well
".
A.
Hougen and
K.
M.
Watson,
Chemical Process Principles,
Part
111,
Wiley, New York (1947),
p. 873. Olaf Andreas Hougen (pronounced "How-gen") (1893-1986) was a leader in the development of
chemical engineering for four decades; together with
K.
M.
Watson and R.
A.
Ragatz, he wrote
influential books on thermodynamics and kinetics.
0.
A.
Hougen and
K.
M.
Watson,
Chemical Process Principles,
Part
11,
Wiley, New York (1947), p.
604.

1.4 Molecular Theory of the Viscosity of Gases at Low Density
23
unless there are chemically dissimilar substances in the mixture or the critical properties
of the components differ greatly.
There are many variants on the above method, as well as a number of other empiri-
cism~. These can be found in the extensive compilation of Reid, Prausnitz, and Poling.'
EXAMPLE
1.3-1
Estimate the viscosity of
NZ
at 50°C and 854 atm, given
M
=
28.0 g/g-mole,
p,
=
33.5 atm, and
T,
=
126.2
K.
Estimation of Viscosity
from Critica
I
Properties
SOLUTION
Using
Eq.
1.3-1 b, we get
p,
=
7.70(28.0)"~(33.5)~'~(126.2)'/~
=
189 micropoises
=
189
X
poise (1.3-3)
The reduced temperature and pressure are
From Fig. 1.3-1, we obtain
p,
=
p/pc
=
2.39. Hence, the predicted value of the viscosity is
p
=
p,(p/p,)
=
(189
X
1OP6)(2.39)
=
452
X
poise
(1.3-5)
The measured value6 is 455
X
lop6
poise. This is unusually good agreement.
1.4
MOLECULAR
THEORY
OF
THE
VISCOSITY
OF
GASES
AT
LOW
DENSITY
To get
a
better appreciation of the concept of molecular momentum transport, we exam-
ine this transport mechanism from the point of view of an elementary kinetic theory of
gases.
We consider a pure gas composed of rigid, nonattracting spherical molecules of di-
ameter
d
and mass
m,
and the number density (number of molecules per unit volume) is
taken to be
n.
The concentration of gas molecules is presumed to be sufficiently small
that the average distance between molecules is many times their diameter
d.
In such
a
gas it is known1 that, at equilibrium, the molecular velocities are randomly directed and
have an average magnitude given
by
(see Problem
1C.1)
7
in which
K
is the Boltzmann constant (see Appendix
F).
The frequency of molecular
bombardment per unit area on one side of any stationary surface exposed to the gas is
R.
C. Reid,
J.
M.
Prausnitz, and
B.
E.
Poling,
The Properties of Gases and Liquids,
McGraw-Hill, New
York, 4th edition (19871, Chapter 9.
A.
M.
J.
F.
Michels and R.
E.
Gibson,
Proc. Roy. Soc.
(London), A134,288-307 (1931).
'
The first four equations in this section are given without proof. Detailed justifications are given in
books on kinetic theory-for example,
E.
H. Kennard,
Kinetic Theory of Gases,
McGraw-Hill, New York
(1938), Chapters
I1
and
111.
Also
E.
A. Guggenheim,
Elements of the Kinetic Theory of Gases,
Pergamon
Press, New York (1960), Chapter
7,
has given a short account of the elementary theory of viscosity. For
readable summaries of the kinetic theory of gases, see R.
J.
Silbey and R. A. Alberty,
Physical Chemistry,
Wiley, New York, 3rd edition (2001), Chapter 17, or R.
S.
Berry,
S.
A. Rice, and
J.
Ross,
Physical Chemistry,
Oxford University Press, 2nd edition (2000), Chapter 28.

24
Chapter 1 Viscosity and the Mechanisms of Momentum Transport
The average distance traveled by a molecule between successive collisions is the
mean
free
path
A,
given by
A
=
1
(1.4-3)
V?ird2n
On the average, the molecules reaching a plane will have experienced their last collision
at a distance
a
from the plane, where
a
is given very roughly by
The concept of the mean free path is intuitively appealing, but it is meaningful only
when
A
is large compared to the range of intermolecular forces. The concept is appropri-
ate for the rigid-sphere molecular model considered here.
To determine the viscosity of a gas in terms of the molecular model parameters, we
consider the behavior of the gas when it flows parallel to the m-plane with a velocity
gradient
dvx/dy
(see Fig. 1.4-1). We assume that Eqs. 1.4-1 to
4
remain valid in this non-
equilibrium situation, provided that all molecular velocities are calculated relative to the
average velocity
v
in the region in which the given molecule had its last collision. The
flux of x-momentum across any plane of constant
y
is found by summing the x-momenta
of the molecules that cross in the positive
y
direction and subtracting the x-momenta of
those that cross in the opposite direction, as follows:
In writing this equation, we have assumed that all molecules have velocities representa-
tive of the region in which they last collided and that the velocity profile
vx(y)
is essen-
tially linear for a distance of several mean free paths. In view of the latter assumption,
we may further write
By combining Eqs. 1.4-2,5, and
6
we get for the net flux of x-momentum in the positive
y
direction
This has the same form as Newton's law of viscosity given in Eq. 1.1-2. Comparing the
two equations gives an equation for the viscosity
1
p
=
nmiiA
=
ipiiA (1.4-8)
Velocity
profile
vx(y)
Fig.
1.4-1
Molecular transport
of x-momentum from the plane at
x
(y
-
a)
to the plane at
y.

4
Molecular Theory of the Viscosity of Gases at Low Density
25
or, by combining Eqs.
1.4-1,3,
and
8
This expression for the viscosity was obtained by Maxwell2
in
1860.
The quantity
d2
is
called the
collision cross section
(see Fig.
1.4-2).
The above derivation, which gives a qualitatively correct picture of momentum
transfer in a gas at low density, makes it clear why we wished to introduce the term
"momentum flux" for
rp
in
§1
.l.
The prediction of Eq. 1.4-9 that
p
is independent of pressure agrees with experimen-
tal data up to about
10
atm at temperatures above the critical temperature (see Fig.
1.3-1).
The predicted temperature dependence is less satisfactory; data for various gases indi-
cate that
p
increases more rapidly than
1/T.
To better describe the temperature depen-
dence of
p,
it is necessary to replace the rigid-sphere model by one that portrays the
attractive and repulsive forces more accurately. It is also necessary to abandon the mean
free path theories and use the Boltzmann equation to obtain the molecular velocity dis-
tribution in nonequilibrium systems more accurately. Relegating the details to Appendix
D,
we present here the main
result^.^'^^
7
of area
d2
,
/--
/
/
/
I
I
Fig.
1.4-2
When two rigid spheres of diameter
d
approach
1
\
each other, the center of one sphere (at
0')
"sees" a circle of
\
\
area
md2
about the center of the other sphere (at
O),
on
/
which a collision can occur. The area
&I2
is
referred to as the
'\
.---/
/
"collision cross section."
--
-
-
-
-
James Clerk Maxwell (1831-1879) was one of the greatest physicists of all time; he is particularly
famous for his development of the field of electromagnetism and his contributions to the kinetic theory
of gases. In connection with the latter, see
J.
C. Maxwell,
Phil. Mag.,
19,19, Prop.
XI11
(1860); S.
G.
Brush,
Am.
J.
Phys,
30,269-281 (1962). There is some controversy concerning Eqs.
1.4-4
and 1.4-9 (see
S.
Chapman
and
T.
G.
Cowling,
The Mathematical Theory of Non-Uniform Gases,
Cambridge University Press, 3rd
edition 1970), p. 98;
R.
E. Cunningham and
R.
J.
J.
Williams,
Diffusion in Gases and Porous Media,
Plenum
Press, New York (1980), s6.4.
Sydney Chapman (1888-1970) taught at Imperial College in London, and thereafter was at the
High Altitude Observatory in Boulder, Colorado; in addition to hs seminal work on gas kinetic theory,
he contributed to kinetic theory
of
plasmas and the theory of flames and detonations. David Enskog
(1884-1947) (pronounced, roughly, "Ayn-skohg") is famous for his work on kinetic theories of low- and
highdensity gases. The standard reference on the Chapman-Enskog kinetic theory of dilute gases is
S.
Chapman and
T.
G.
Cowling,
The Mathematical Theory of Non-Uniform Gases,
Cambridge University
Press, 3rd edition (1970); pp. 407409 give a historical summary of the kinetic theory. See also
D.
Enskog,
Inaugural Dissertation,
Uppsala (1917).
In
addition
J.
H.
Ferziger and
H.
G.
Kaper,
Mathematical Theory of
Transport Processes in Gases,
North-Holland, Amsterdam (1972), is a very readable account of molecular
theory.
The Curtiss-Hirschfelder5 extension of the Chapman-Enskog theory to multicomponent gas
mixtures, as well as the development of useful tables for computation, can be found in
J.
0.
Hirschfelder,
C.
F.
Curtiss, and
R.
B.
Bird,
Molecular Theory of Gases and Liquids,
Wiley, New York, 2nd corrected printing
(1964). See also C.
F.
Curtiss,
J.
Chem. Phys.,
49,2917-2919 (19681, as well as references given in Appendix
E.
Joseph Oakland Hirschfelder (1911-1990), founding director of the Theoretical Chemistry Institute at
the University of Wisconsin, specialized in intermolecular forces and applications of kinetic theory.
C.
F.
Curtiss and
J.
0.
Hirschfelder,
J.
Chem. Phys.,
17,550-555 (1949).

26
Chapter
1
Viscosity and the Mechanisms of Momentum Transport
A
rigorous kinetic theory of monatomic gases at low density was developed early in
the twentieth century by Chapman in England and independently by Enskog in Sweden.
The Chapman-Enskog theory gives expressions for the transport properties in terms of
the intermolecular potential energy
&),
where r is the distance between a pair of molecules
undergoing a collision. The intermolecular force is then given by F(r)
=
-dp/dr. The
exact functional form of p(r) is not known; however, for nonpolar molecules a satisfac-
tory empirical expression is the Lennard-Jones
(6-12)
potential6 given by
in which
a
is a characteristic diameter of the molecules, often called the collision diameter
and
E
is a characteristic energy, actually the maximum energy of attraction between a
pair of molecules. This function, shown in Fig. 1.4-3, exhibits the characteristic features
of intermolecular forces: weak attractions at large separations and strong repulsions at
small separations. Values of the parameters
a
and
E
are known for many substances; a
partial list is given in Table E.l, and a more extensive list is available el~ewhere.~ When
u
and
E
are not known, they may be estimated from properties of the fluid at the critical
point (c), the liquid at the normal boiling point
(b),
or the solid at the melting point (m),
by means of the following empirical relations:"
Here
E/K
and
T
are in
K,
a
is in &tgstriim units (1
A
=
lop1'
m), ?is in ~rn~/~-rnole, and
p,
is in atmospheres.
The viscosity of a pure monatomic gas of molecular weight
M
may be written in
terms of the Lennard-Jones parameters as
Molecules repel Molecules attract
one another at
one another at
separations
r
<
r,,
separations
r
>
r,
I
I
I
Whenr
-3u,
llcp(
I
has dropped off
to less than 0.01
E
Fig.
1.4-3
Potential energy function
0
-
p(r) describing the interaction of two
r
spherical, nonpolar molecules. The
Lennard-Jones
(6-12)
potential, given
in
Eq.
1.4-10,
is one of the many em-
pirical equations proposed for fitting
this curve. For r
<
Y,
the molecules
repel one another, whereas for r
>
r,
the molecules attract one another.
J.
E.
(Lennard-)Jones,
Proc. Roy. Soc.,
A106,441462,463477 (1924). See also
R.
J.
Silbey and
R.
A.
Alberty,
Physical
Chemistry,
Wiley, 2nd edition (2001), §§11.10,16.14, and 17.9;
and
R.
S. Berry,
S.
A.
Rice,
and
J.
Ross,
Physical Chemistry,
Oxford University Press, 2nd edition (2000), g10.2.
